Лекции Гармонический анализ. Гармонический анализ
 Скачать 1.04 Mb. Скачать 1.04 Mb.
|
|
§ 4. Разложение в ряд Фурье четных и нечетных функций периода 2. Определение 12. Функция f(x) называется четной, если она не меняется при изменении знака ее аргумента, т.е. если f(–х) = f(x). График четной функции симметричен относительно оси координат. Определение 13.Функция f(x) называется нечетной, если при изменении знака аргумента она меняет знак, но сохраняет абсолютную величину, т.е. если f(–х) = – f(x). График нечетной функции симметричен относительно начала координат. Функция может не быть ни четной, ни нечетной. Теорема 5. Произведение двух функций одинаковой (различной) четности четно (нечетно). Сумма четных функций – четная функция, нечетных функций – нечетная. Лемма. Верна формула Теорема 6. Если f(x) четна, то Если же f(x) нечетна, то Пусть f(x) – четная функция, тогда ее коэффициент Фурье а0 по формуле (1.15) может быть записан в виде а0 = Поскольку произведение f(x) cos nx четно по теореме 5, то по той же формуле (1.15) аn = bn = 0, так как произведение f(x) sin nx нечетно по теореме 5 и к bn применима формула (1.16). Отсюда следует Теорема 7. Ряд Фурье четной функции f(x) не содержит членов с синусами и имеет вид: f(x) = причем его коэффициенты можно находить по упрощенным формулам (1.17), (1.18). Таким же способом устанавливается Теорема 8. Ряд Фурье нечетной функции f(x) не содержит ни свободного члена, ни членов с косинусами и имеет вид: гдеbn= Пример 2. Разложить в ряд Фурье функцию, определенную равенством f(x) = x при – < x . Решение: f 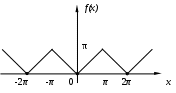 (x) имеет период 2, удовлетворяет условиям теоремы, т.е. разлагается в ряд Фурье. f(–x) = f(x), т.е. она четная. (См. рис. 3.) (x) имеет период 2, удовлетворяет условиям теоремы, т.е. разлагается в ряд Фурье. f(–x) = f(x), т.е. она четная. (См. рис. 3.)По формулам (1.17) и (1.18) найдем коэффициенты Фурье: а0 = аn = 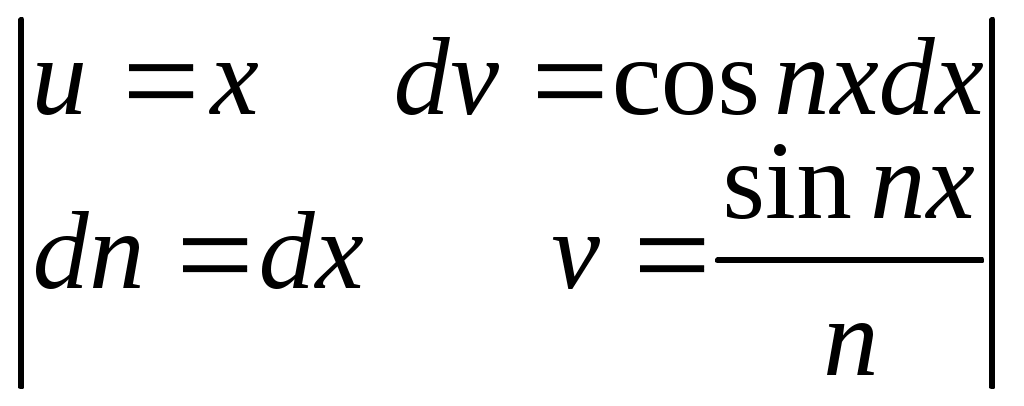 = == 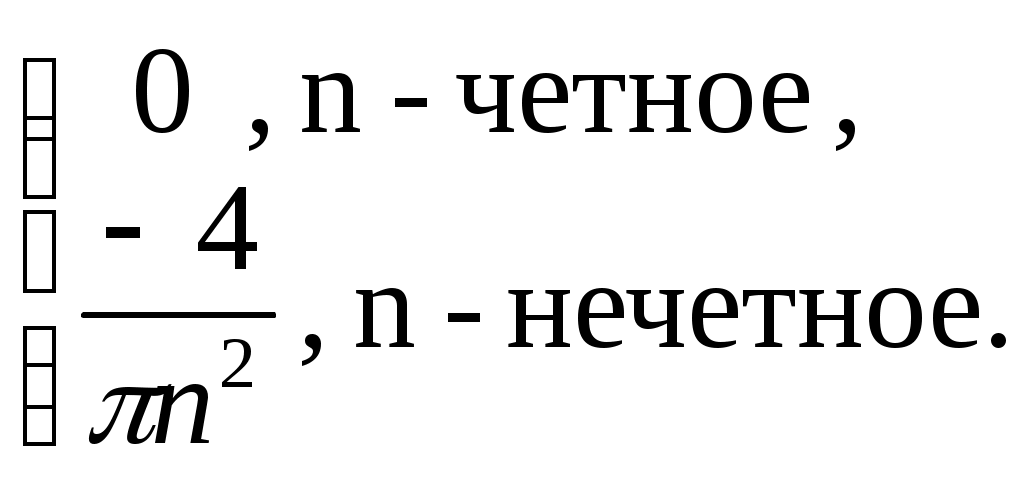 Следовательно, ряд Фурье для данной функции имеет вид: f(x) = На интервале [–; ] ряд сходится к функции x . Пример 3. Разложить в ряд Фурье функцию: f(x)= 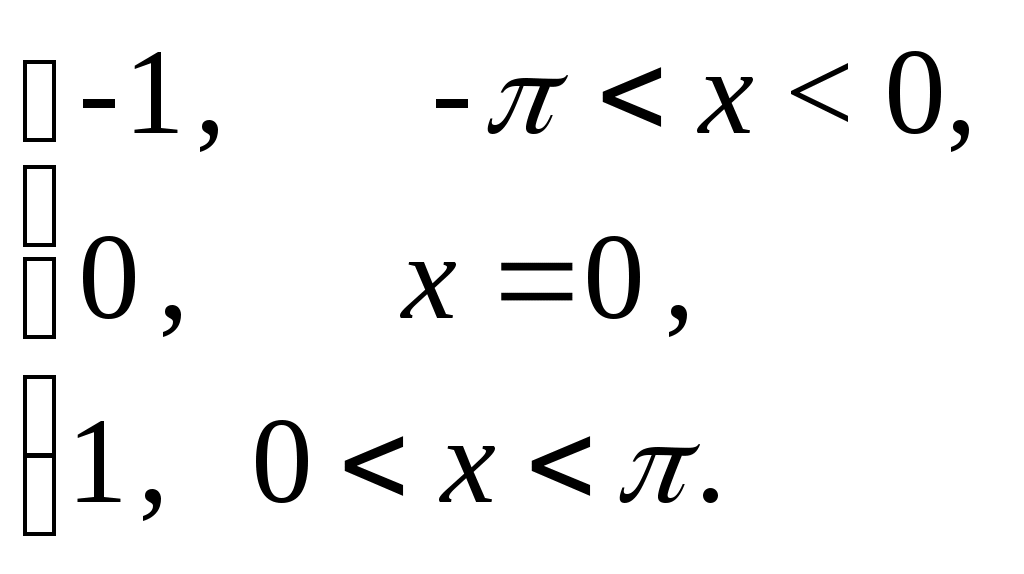 Решение: f(x) имеет период 2. Она удовлетворяет условиям теоремы, т.е. разлагается в ряд Фурье. f(–х) = – f(x) (см. рис. 4), т.е. f(x) – нечетна, следовательно а0 = 0 и аn= 0. 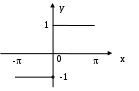 Рис. 4. По формуле (1.21) найдем коэффициент Фурье: b n = 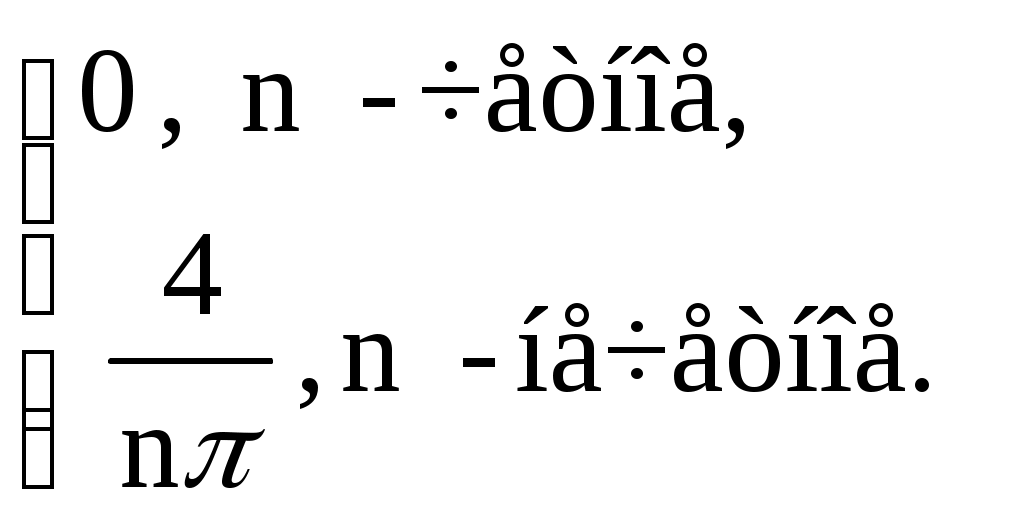 b2k+1 = Следовательно, ряд Фурье для данной функции имеет вид: f(x) = f(x) = На интервале [–; ] ряд сходится к функции f(x), в точках х = 0 и х = – к нулю. § 5. Сдвиг основного промежутка. Вся теория рядов Фурье излагалась для функций, заданных на отрезке [–; ], однако вместо этого отрезка можно было бы положить в основу рассуждения любой другой отрезок длины 2, так как 2 есть период всех функций системы 1, cos x, sin x, cos 2x, …, и справедлива Теорема 9. Если функция f(x) имеет период 2, то интеграл Теорема 10. Если f(x) дифференцируема на отрезке [0; 2], то всюду на открытом промежутке (0, 2) будет f(x) = а0 = аn= bn= ряд сходится в точках x= 0, x= 2, где его сумма равна ( без доказательства) Пример 4. Разложить в ряд Фурье функцию f(x) = x, заданную на отрезке [0; 2]. 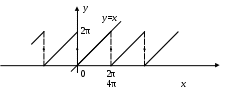 Рис. 5. Решение: График функции изобразим на рис. 5. Видно, что функция – разрывная. Найдем коэффициенты Фурье. Здесь а0 = аn = bn = Стало быть, при 0 < x < 2π будет x = В точках x= 0 и x= 2 сумма S(x) ряда равна . § 6. Разложение в ряд Фурье функций с периодом 2ℓ. Пусть функция f(x) задана и дифференцируема на отрезке [–l; l]. Положим φ(z) = Тогда φ(z) будет заданной и дифференцируемой уже на отрезке [–π; π].Значит к φ(z) применима теория, изложенная выше, поэтому при – π < z< π будет φ(x) = Положим в этом равенстве f(x) = где а0 = Если f(x) – четная, то где а0 = Если f(x) – нечетная, то где bn= Замечание. Можно от периода 2 Пример 5. Разложить в ряд Фурье функцию f(x) = x, заданную на интервале –2 х 2. Решение: 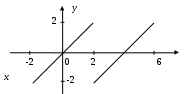 Рис. 6 График функции f(x) = x изображен на рисунке 6. Видно, что функция нечетная с периодом 2ℓ = 4, то есть ℓ = 2. Найдем коэффициенты Фурье по формуле 1.30. bn= = – = 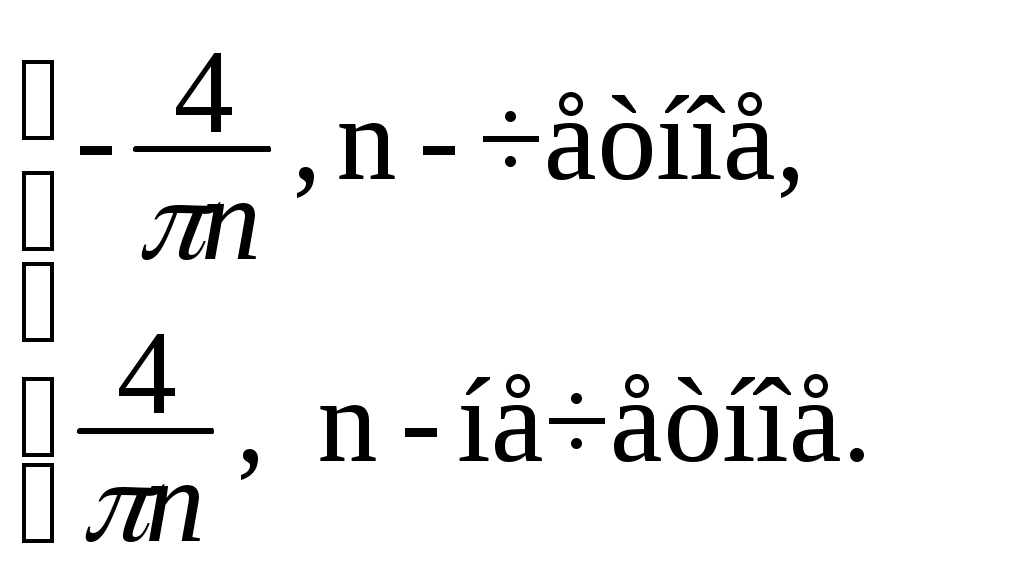 Следовательно, по 1.29 разложение в ряд Фурье функции f(x) имеет вид: f(x) = x = Пример 6. Разложить в ряд Фурье функцию f(x) = 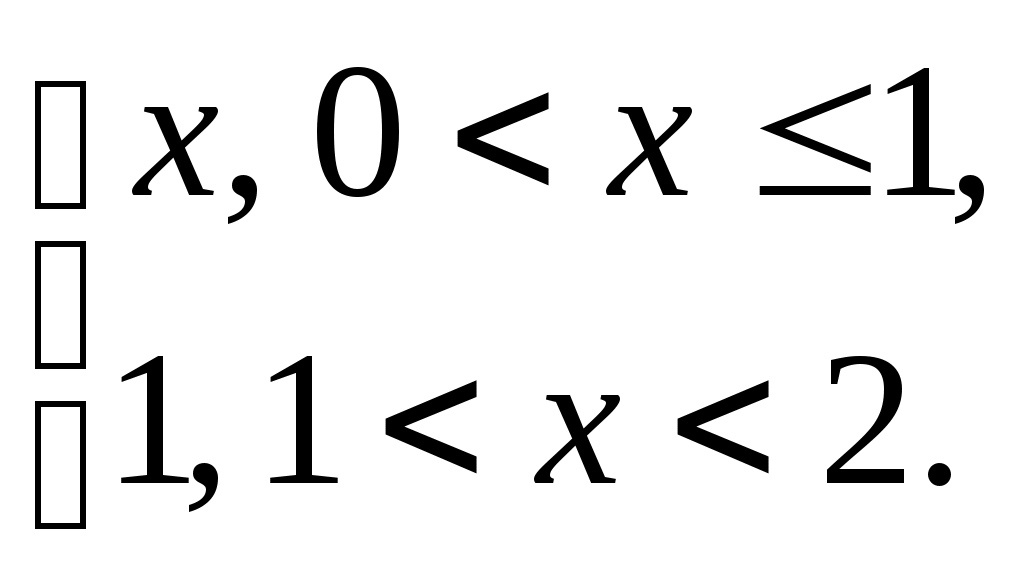 Решение: Воспользуемся замечанием. Произведем замену переменой х = f при 0 < х / < . при - < х / 0, (x) = 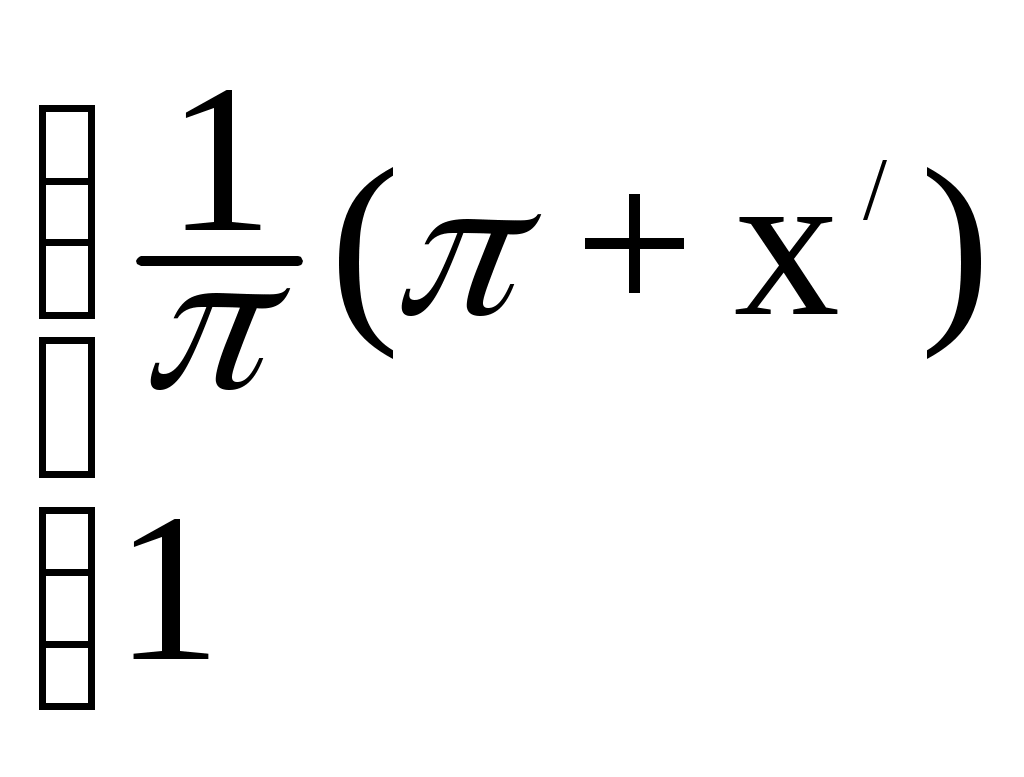 Найдем коэффициенты Фурье. а 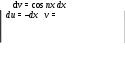 0 = 0 = an= = 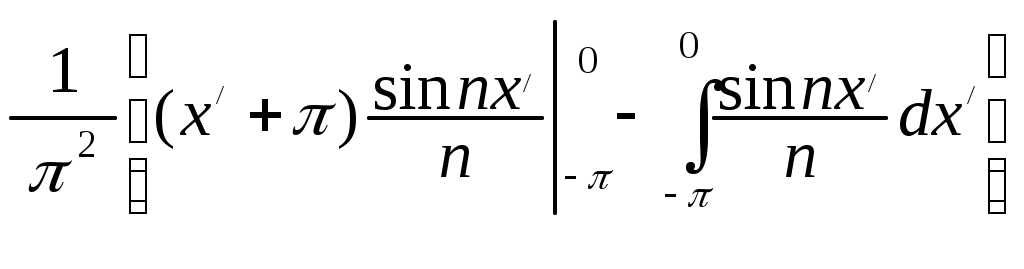 + + = n – четное n – нечетное. bn = Следовательно, f(x) = |
