Лекции Гармонический анализ. Гармонический анализ
 Скачать 1.04 Mb.
|
|
§ 7. Разложение в ряд Фурье функций, заданных на полупериоде. Пусть требуется разложить в ряд Фурье функцию f(x), заданную на полупериоде, т.е. в интервале (0, p) или (0, l). В этом случае можно произвольно продолжить функцию f(x) на интервал (–, 0) или (–l,0) но так, чтобы образовавшаяся в этом интервале новая функция F(x), совпадающая с f(x) в интервале (0, ) или (0, l), удовлетворяла условиям основной теоремы. Разложив F(x) в ряд Фурье на интервале (-, p) или (-l, l), получим искомый ряд, представляющий f(x) в интервале (0, p) или (0, l), и не имеет значения, что он в интервале (–,0) или (–l,0) представляет какую-то другую функцию, по существу не связанную с данной функцией f(x). В частности, f(x) можно продолжить четно на интервал (–,0) или (–l,0), значит график f(x) надо продолжить симметрично относительно оси (оу). Тогда F(x) – четная функция, и ряд будет состоять только из косинусов. Если f(x) продолжить нечетно на интервал (–,0) или (–l,0), значит график f(x) продолжить симметрично относительно начала координат, то F(x) будет нечетной, и ряд будет состоять только из синусов. Т.е. можно составить сколько угодно сходящихся тригонометрических рядов, представляющих в интервале (0,) или (0,l) одну и ту же функцию, а в интервале (–,0) или (–l,0) самые разнообразные функции. Функцию, заданную на полупериоде [0; ], можно разложить в ряд синусов или ряд косинусов, продолжая на второй полупериод соответственно нечетным или четным образом. Пример 7. Функцию f(x) =  –  разложить в ряд косинусов на интервале (0; ).Решение: Так как требуется разложить в ряд косинусов, то надо продолжить функцию четным образом, то есть ее график будет симметричен относительно оси (оу). На рисунке 7 изображен график полученной четной функции: на заданном интервале (0; ) – сплошной линией, на интервале (–; 0) – пунктиром . 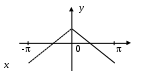 Рис. 7. Найдем коэффициенты Фурье по формулам (1.17)–(1.18): 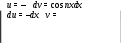 =  =  =  = 0 аn =  = 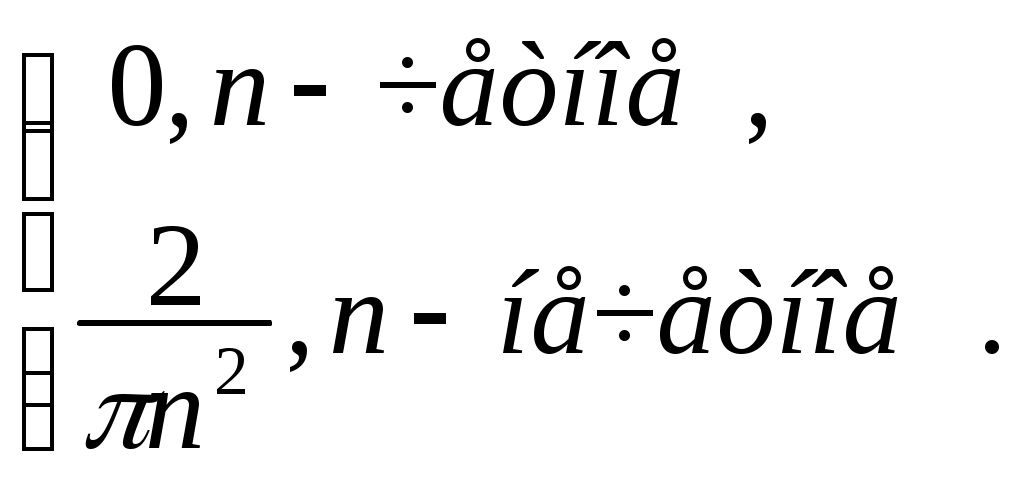= ==    +  nxdx = –  =  – (–1)n = = [ 1 – (–1) n] =  а2n+1 =  k =0,1,2, …С f(x) =  –  =  .§ 8. Разложение в ряд Фурье функций с “двойной симметрией”. Опеделение14. Если функция f(x) периода 2ℓ четная или нечетная и удовлетворяет условию f(ℓ–x) = f(x), то говорят, что f(x) обладает двойной симметрией. В этом случае, если f(x) – четная, то ее коэффициенты Фурье приобретают вид: а2n=  x ) cos dx; а2n+1 = 0 ( n = 0,1,2,…), bn = 0 ( n = 0,1,2,…).Если же f(x) – нечетная, то ее коэффициенты Фурье определяются так: аn = 0 ( n = 0,1,2,…), b2n = 0 , b2n+1 =  x ) sin dx, ( n = 0,1,2,…).§ 9. Интеграл Фурье. 2.1. Интеграл Фурье и двойной интеграл Фурье. Определение 15. Функция f(x) называется кусочно-гладкой на отрезке [а,b], если: 1) она непрерывна на этом отрезке или имеет конечное число точек разрыва первого рода; 2) этот отрезок можно разбить на конечное число частичных отрезков, на каждом из которых f(x) обладает непрерывной производной, т.е. является гладкой. Определение 16. Функция f(x) называется абсолютно интегрируемой на всей числовой оси, если сходится несобственный интеграл от ее модуля  Теорема 11. Если f(x) имеет на каждом конечном интервале не более конечного числа точек разрыва и абсолютно интегрируема на (-∞, ∞), то в каждой точке x,в которой f(x) дифференцируема, имеем: f(x) =  . (2.1)Правая часть формулы (2.1) называется двойным интегралом Фурье функции f(x). Так как cos u(t–x) = cos ut·cos ux + sin ut · sin ux, то (после внесения множителя 1/π) внутренний интеграл в формуле (2.1) можно преобразовать так:   где  u ≥ 0, (2.2) u ≥ 0. (2.3)Тогда (2.1) принимает вид:  (2.4) Определение 17.Выражение, стоящее в правой части формулы (2.4), называется интегралом Фурье для функции f(x). Таким образом, функция f(x) представляется своим интегралом Фурье во всех точках дифференцируемости. В точках разрыва левая часть формулы (2.4) должна быть заменена на  ].Замечание. В теореме 13 сформулировано достаточное условие представимости функции своим интегралом Фурье. Оно не является необходимым, представимость интегралом Фурье будет иметь место и при более общих условиях. Формула (2.4) показывает, что интеграл Фурье можно рассматривать как континуальный аналог ряда Фурье: вместо суммирования по индексу n, пробегающему целые значения, мы имеем интегрирование по непрерывно изменяющемуся переменному u; вместо коэффициентов Фурье, зависящих от целого индекса n, мы имеем функции a(u), b(u) от непрерывно изменяющегося переменного u, определяемые формулами (2.2), (2.3). Пример 8. Представить интегралом Фурье функцию 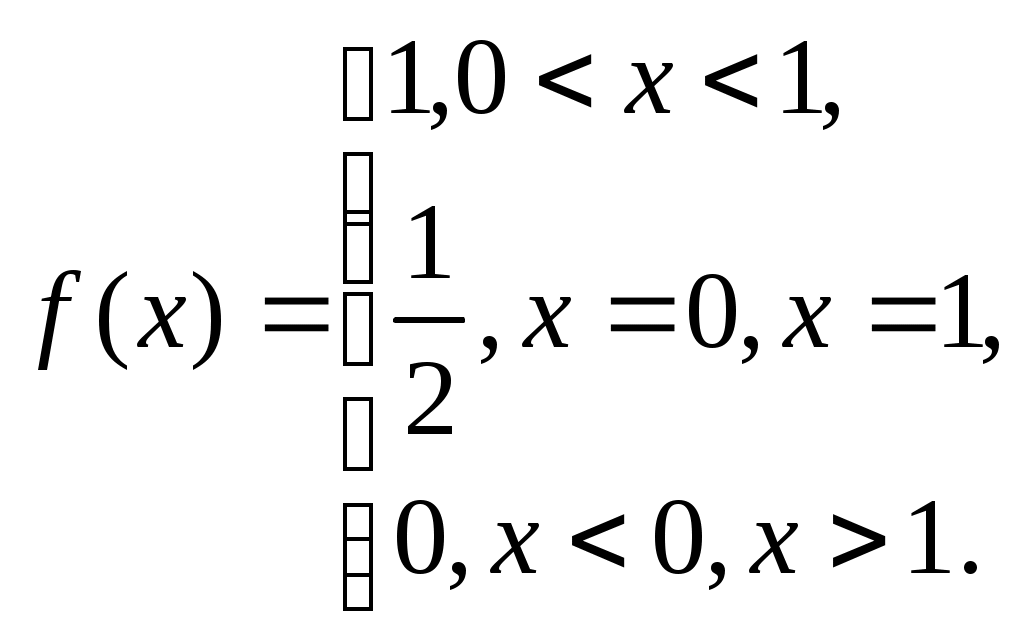 Решение: Данная функция является кусочно-гладкой, так как она состоит из трех гладких частей: y = 0 на (-∞; 0), y = 1 на (0;1) и y = 0 на (1; ∞) и имеет две точки разрыва первого рода при x= 0, x = 1. Она абсолютно интегрируема на всей числовой оси, так как вне отрезка [0;1] она равна нулю, и интеграл от нее по всей числовой оси сведется к интегралу по отрезку [0;1]. Следовательно, такая функция может быть представлена интегралом Фурье. По формуле (2.1) имеем f(x) = 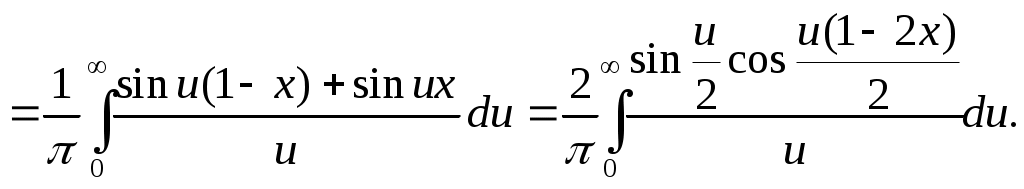=   В точках x= 0, x = 1, где функция терпит разрыв, полученное представление сохраняется, так как в этих точках 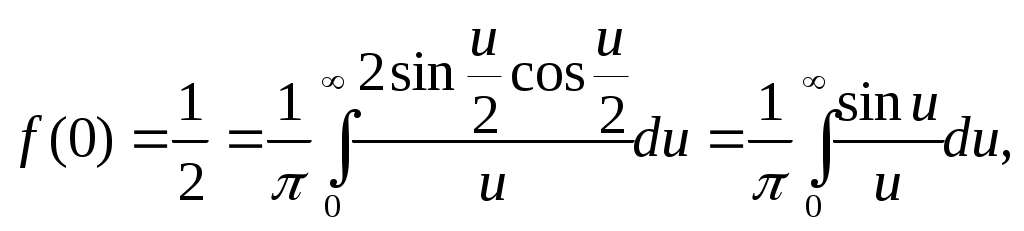] =  = f(x). В частности, при x= 0 получим что равносильно равенству  2.2. Интеграл Фурье для четных и нечетных функций. Если f(x) – четная функция, то   , (2.5)и ее представление интегралом Фурье имеет вид:  (2.6)Или в виде двойного интеграла Фурье: f(x)=  (2.7)Если f(x) – нечетная функция, то  , (2.8)и ее представление интегралом Фурье имеет вид:  (2.9)Или в виде двойного интеграла Фурье: f(x)=  . (2.10)Пример 9. Представить интегралом Фурье функцию f(x) = 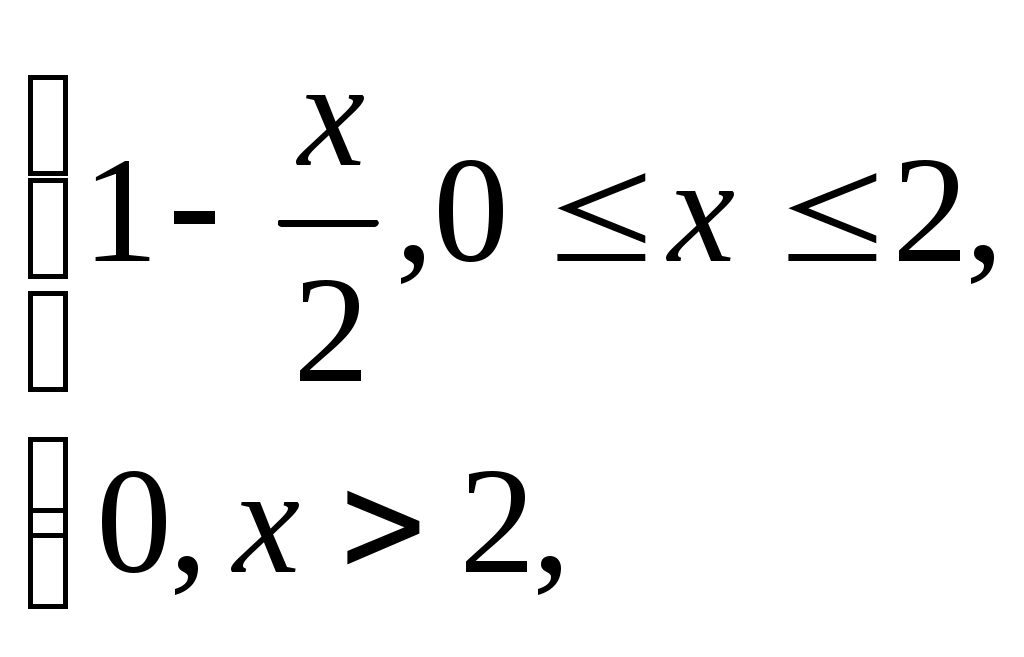 продолжив ее четным образом для отрицательных значений.Решение: Заданная четная функция, очевидно, удовлетворяет указанным выше условиям представления в виде интеграла Фурье, поэтому к ней можно применить формулу (2.7), в которой интегрировать f(t) надо только по отрезку [0,2], так как вне этого отрезка она равна нулю. По формуле (2.7) имеем: f(x) =  .Вычислим отдельно внутренний интеграл (по частям):   Следовательно, f(x) =  ;в частности, при x = 0 получаем f(0) = 1 =  , то есть  .Пример 10. Представить интегралом Фурье функцию f(x) = 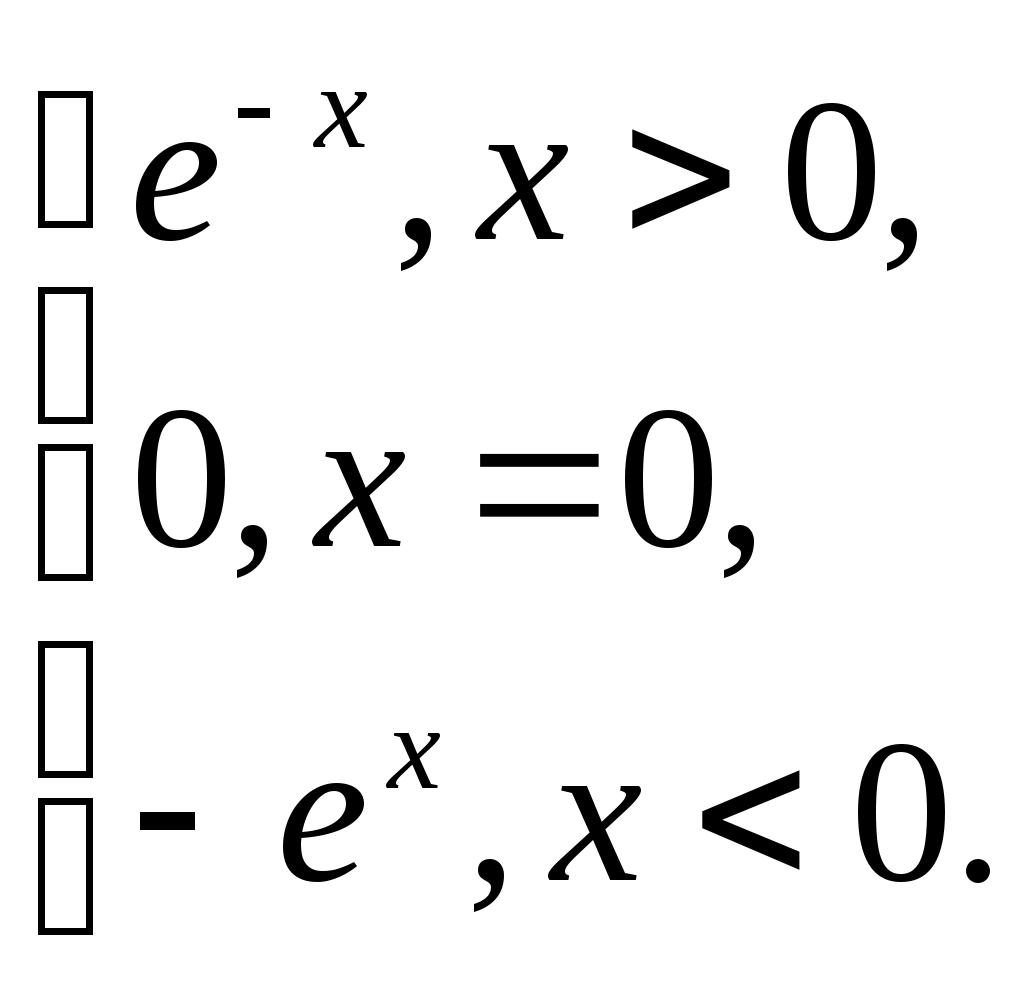 Решение: 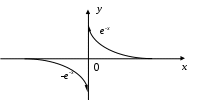 Рис. 8. Данная функция является кусочно-гладкой, так как состоит из двух гладких частей и имеет разрыв первого рода в точке x = 0. (См. рис. 8) Проверим, что f(x) абсолютно интегрируема на всей числовой оси. Для этого убедимся, что сходится интеграл:  =  (1 – 0) – (0 – 1) = 2.Следовательно, функцию можно представить интегралом Фурье, а поскольку она является нечетной, то можно воспользоваться формулой (2.10): f(t) =  .Интегрированием по частям найдем внутренний интеграл  .Вторично интегрируя по частям, получим:  откуда  Таким образом, представление интегралом Фурье функции имеет вид:  2.3. Комплексная форма интеграла Фурье. Определение 18. Если f(x) – имеет на каждом конечном интервале лишь конечное число точек разрыва первого рода и абсолютно интегрируема на всей числовой оси, то в каждой точке x, в которой f(x) дифференцируема, выполняется равенство  (2.11)Где  (2.12)Функцию c(u) называют преобразованием Фурье функции f(t), или (учитывая физические соображения) спектральной характеристикой функции f(t).  называется амплитудным спектром функции f(t). Выражение f(x) по формуле (2.11) называют комплексной формой интеграла Фурье (или обратным преобразованием Фурье).Подстановка (2.12) в (2.11) приводит к двойному интегралу Фурье в комплексной форме:  (2.13)Пример 11. Найти спектральную функцию и амплитудный спектр функции 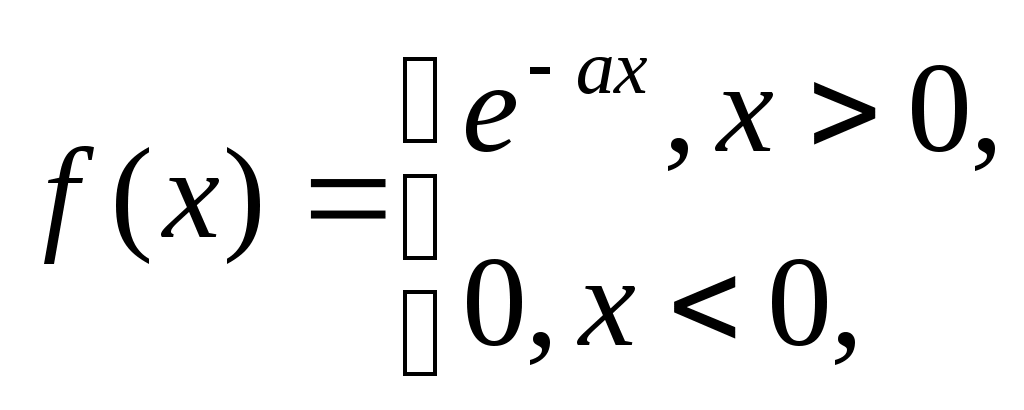 a> 0.Представить f(x) комплексной формой интеграла Фурье. Решение: По формуле (2.12) находим спектральную функцию, учитывая, что при t< 0 f(t) =0:  Амплитудный спектр  =  Комплексная форма (2.11) интеграла Фурье данной функции имеет вид  |