механика. Билет 7 Законы трения
 Скачать 1.1 Mb. Скачать 1.1 Mb.
|
| Билет 5 1.Закон сохранения импульса Закон сохранения — закон, утверждающий, что сумма импульсов всех тел системы есть величина постоянная, если векторная сумма внешних сил, действующих на систему тел, равна нулю. В классической механике закон сохранения импульса обычно выводится как следствие законов Ньютона. Из законов Ньютона можно показать, что при движении системы в пустом пространстве импульс сохраняется во времени, а при наличии внешнего воздействия скорость изменения импульса определяется суммой приложенных сил. Закон сохранения импульса впервые был сформулирован Декартом. Импульс тела (материальной точки) представляет собой векторную величину, равную произведению массы тела на скорость тела: Направление импульса всегда совпадает с направлением скорости, так как m > 0, то Любое движущееся тела имеет импульс. Единица измерения импульса: Произведение силы на время её действия называется импульсом силы. Второй закон Ньютона в импульсной форме. Изменение импульса тела (материальной точки) равно импульсу действующей на него силы: Импульс тела равен сумме импульсов отдельных его элементов: Импульс системы тела равен векторной сумме импульсов каждого из тел системы: Импульс обладает интересным свойством сохраняться, которое есть только у нескольких физических величинах. Силы, с которыми взаимодействуют тела системы друг с другом, называются внутренними, а силы, создаваемые телами, которые не принадлежат этой системе, являются внешними силами. Система, в которой внешние силы не действуют или сумма внешних сил равна нулю, называется замкнутой. Полный импульс тел сохраняется, в замкнутой системе тела могут только обмениваться импульсами. Столкновение тел представляет собой взаимодействие тел при их относительном перемещении. Абсолютно неупругий удар - это столкновение двух тел, которые объединяются и движутся дальше как одно целое. Закон сохранения импульса при неупругом ударе: Абсолютно упругий удар - столкновение тел, при котором тела не соединяются в одно целое и их внутренние энергии остаются неизменными. Закон сохранения импульса при упругом ударе: Закон сохранения импульса. Если внешние силы на систему не действуют или их сумма равна нулю, то импульс системы остается неизменным: Закон сохранения импульса является одним из основных законов физики. Границы применимости закона сохранения импульса: замкнутая система. Закон сохранения импульса с честью выдержал испытание временем и до сих пор он продолжает свое триумфальное шествие. Он дал неоценимый инструмент для исследования ученым, как один из фундаментальных законов физики, ставя запрет одним процессам и открывая дорогу другим. Действие этого закона проявляется в науке, в технике, в природе и в повседневной жизни. Всюду этот закон работает отлично - реактивное движение, атомные и ядерные превращения, взрыв и т.д. Во многих повседневных ситуациях помогает разобраться понятие импульса. Рене Декарт попытался использовать термин «импульс» вместо силы. Это связано с тем, что силу трудно измерить, а массу и скорость измерить несложно. Поэтому вместо импульса часто говорят количество движения (Именно Ньютон первым назвал произведение массы тела на скорость количеством движения). Декарт понимал большое значение понятия количества движения — или импульса тела — как произведения массы тела на скорость. Но он совершил ошибку, не рассматривая количество движения как векторную величину. Ошибка эта была исправлена в начале XVIII века. Используя закон сохранения импульса можно «найти» и невидимые объекты, например, электромагнитные волны, излучаемые открытым колебательным контуром, или антинейтрино – субатомные частицы, не оставляющие следов в детекторах. 2.Гидростатика несжимаемой жидкости. Закон Архимеда. Основной закон гидростатики для несжимаемой жидкости в однородном поле тяжести имеет вид В случае движущейся несжимаемой жидкости можно условно говорить о справедливости закона Паскаля( Давление, производимое на жидкость передается в любую точку без изменений во всех направлениях) При этом для гидростатического давления в данной точке несжимаемой жидкости будем иметь: +Р=Ро+yh Это и есть уравнение гидростатики для несжимаемой жидкости, когда из объемных сил на нее действуют только силы тяжести. Закон Архимеда был открыт в 3-м веке до н.э. В современной формулировке он гласит: На всякое тело, погруженное в жидкость, (или газ) действует со стороны этой жидкости (или газа) выталкивающая сила, равная весу вытесненной этим телом жидкости. Сила Архимеда направлена вверх и приложена к геометрическому центру погруженной части тела Чтобы тело, погруженное в жидкость полностью или частично, находилось в равновесии, нужно, чтобы сумма сил,действующих на тело, была равноЭто условие плавания тел. В зависимости от формы плавающего тела и положения его центра тяжести равновесие может быть устойчивым, неустойчивым и безразличным. Точка приложения равнодействующей сил Архимеда называется центром плавучести. Если центр плавучести выше центра тяжести, то положение равновесия устойчивое, если ниже - неустойчивое. Если точки A и С совпадают, равновесие безразличное. | Билет 18 1. Момент силы и момент импульса относительно неподвижной оси. Момент инерции. Моментом силы F относительно неподвижной точки О называется векторная физическая величина, определяемая векторным произведением радиус-вектора r, проведенного из точки О в точку А приложения силы, на силу F. M=[r;F] Модуль момента силы равен M=Frsinα=Fl, где α – угол между r и F, l=rsinα - плечо силы F (l – длина перпендикуляра, опущенного из точки О на направление действия силы. 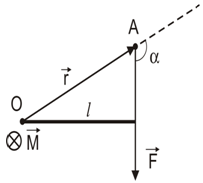 Направление вектора M совпадает с направлением поступательного движения правого винта при его кратчайшем повороте от r и F. Моментом силы относительно неподвижной оси z называется скалярная величина Mz, равная проекции на эту ось вектора M момента силы , определенного относительно произвольной точки О данной оси z. Осевой момент импульса - момент импульса относительно неподвижной оси - это скалярная величина, равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки на этой оси. Производная момента импульса относительно оси равна моменту действующих сил относительно этой же оси. Момент инерции — скалярная физическая величина, мера инерции во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости). Единица измерения в Международной системе единиц (СИ): кг·м². Обозначение: I или J. Различают несколько моментов инерции — в зависимости от типа базового множества, до которого отсчитываются расстояния от элементарных масс. Моментом инерции механической системы относительно неподвижной оси («осевой момент инерции») называется величина Ja, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси. 2. Закон сохранения и симметрия пространства-времени. В основе закона сохранения энергии лежит однородность времени, т.е. равнозначность всех моментов времени (симметрия по отношению к сдвигу начала отсчета времени). Равнозначность следует понимать в том смысле, что замена момента времени t1 на момент времени t2, без изменения значений координат и скорости частиц, не изменяет механические свойства системы. Это означает то, что после указанной замены, координаты и скорости частиц имеют в любой момент времени t2 + t такие же значения, какие имели до замены, в момент времени t1 + t. В основе закона сохранения импульса лежит однородность пространства, т. е. одинаковость свойств пространства во всех точках (симметрия по отношению к сдвигу начала координат). Одинаковость следует понимать в том смысле, что параллельный перенос замкнутой системы из одного места пространства в другое, без изменения взаимного расположения и скоростей частиц, не изменяет механические свойства системы. В основе закона сохранения момента импульса лежит изотропия пространства, т. е. одинаковость свойств пространства по всем направлениям (симметрия по отношению к повороту осей координат). Одинаковость следует понимать в том смысле, что поворот замкнутой системы, как целого, не отражается на её механических свойствах. Между законами типа основного уравнения динамики и законами сохранения имеется принципиальная разница. Законы динамики дают нам представление о детальном ходе процесса. Так, если задана сила, действующая на материальную точку и начальные условия, то можно найти закон движения, траекторию, величину и направление скорости в любой момент времени и т.п. Законы сохранения не дают нам прямых указаний на то, как должен идти тот или иной процесс. Они говорят лишь о том, какие процессы запрещены и потому в природе не происходят. Таким образом, законы сохранения проявляются как принципы запрета: любое явление, при котором не выполняется хотя бы один из законов сохранения, запрещено, и в природе такие явления никогда не наблюдаются. Всякое явление, при котором не нарушается ни один из законов сохранения, в принципе может происходить. | ||||
| Билет №8 1.Импульс силы. Теорема о движении центра масс. Импульс силы — это мера воздействия силы на тело за данный промежуток времени (в поступательном движении). За конечный промежуток времени он равен определенному интегралу от элементарного импульса силы, где пределами интегрирования являются моменты начала и конца промежутка времени действия силы Теорема о движении центра масс (центра инерции) системы — одна из общих теорем динамики, является следствием законов Ньютона. Утверждает, что ускорение центра масс механической системы не зависит от внутренних сил, действующих на тела системы, и связывает это ускорение с внешними силами, действующими на систему Теорема о движении центра масс системы: Произведение массы системы на ускорение ее центра масс равно геометрической сумме всех действующих на систему внешних сил: ma=(сумма F) 2. Деформация кручения Кручение — один из видов деформации тела. Возникает в том случае, если нагрузка прикладывается к телу в виде пары сил в его поперечной плоскости. При этом в поперечных сечениях тела возникает только один внутренний силовой фактор — крутящий момент. Примеры кручения: пружины растяжения-сжатия, валы. При деформации кручения смещение каждой точки тела перпендикулярно к её расстоянию от оси приложенных сил и пропорционально этому расстоянию. Угол закручивания цилиндрического стержня в границах упругих деформаций под действием момента T может быть определён из уравнения закона Гука для случая кручения 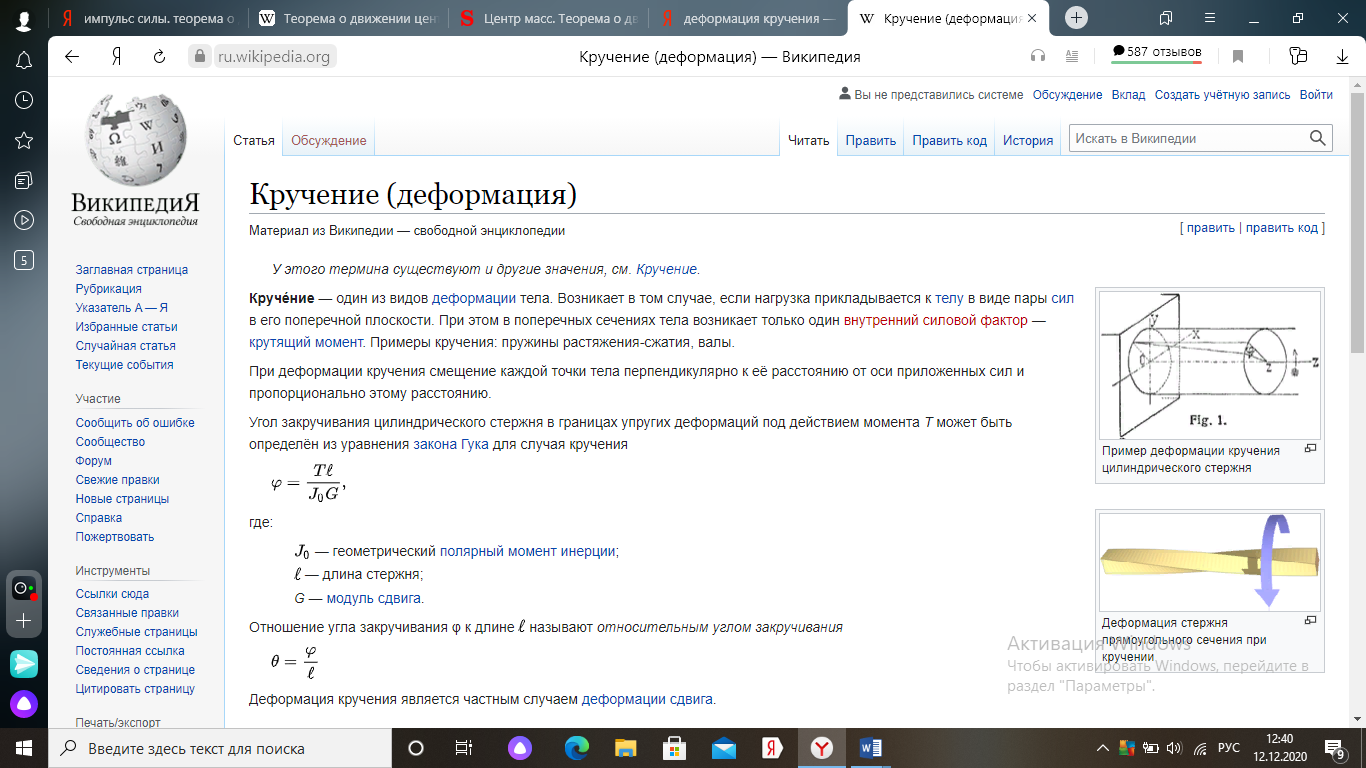 {\displaystyle \varphi _{}={T\ell \over J_{0}G},} {\displaystyle \varphi _{}={T\ell \over J_{0}G},} | Билет №15 1. Абсолютно упругий и неупругий удары Удар (или соударение) — столкновение двух и более тел, при котором происходит изменение скоростей тел за очень короткое время. Абсолютно упругий удар — удар, при котором механическая энергия взаимодействующих тел системы не изменяется. Удар называется центральным, если тело до удара движется вдоль прямой, проходящей через их центры масс. Абсолютно неупругий удар — удар, в результате которого тела движутся как единое целое с одинаковой скоростью либо покоятся. Для абсолютно упругого удара выполняются закон сохранения импульса и закон сохранения кинетической энергии. При центральном абсолютно неупругом ударе вследствие деформации взаимодействующих тел закон сохранения механической энергии не соблюдается; имеет место закон сохранения суммарной энергии различных видов — механической и внутренней. Скорости шаров после центрального абсолютно упругого удара: 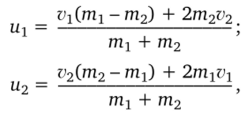 где т1 и т2 — массы шаров; и v2 — их скорости до удара. Скорость шаров после центрального абсолютно неупругого удара: где т1ит2 — массы шаров; и v2 — их скорости до удара. Механическая энергия системы шаров после центрального неупругого удара, перешедшая частично в тепловую и другие формы энергии: Коэффициент полезного действия (КПД) механизма — отношение полезной работы Апол ко всей совершенной (затраченной) работе Лзатр: 2. Скатывание тел с наклонной плоскости Под этим движением понимают перемещение некоторого объекта вдоль плоской поверхности, которая наклонена под определенным углом к горизонту. Примерами может служить соскальзывание бруска по доске или качение цилиндра по металлическому наклоненному листу. Для определения характеристик рассматриваемого типа движения необходимо в первую очередь найти все силы, которые действуют на тело (брусок, цилиндр). Они могут быть разными. В общем случае это могут быть следующие силы: тяжести; реакции опоры; трения качения и/или скольжения; натяжение нити; сила внешней тяги. Первые три из них присутствуют всегда. Существование последних двух зависит от конкретной системы физических тел. Чтобы решать задачи на перемещение по плоскости наклонной необходимо знать не только модули сил, но и их направления действия. В случае, если тело по плоскости скатывается, сила трения неизвестна. Однако она определяется из соответствующей системы уравнений движения. | ||||
| Билет №11 1.Энергию, которой обладает тело вследствие своего движения, называют кинетической энергией. Работа силы равна изменению кинетической энергии тела. Это утверждение называют теоремой о кинетической энергии. Если сила совершает положительную работу, то кинетическая энергия тела увеличивается. Скорость тела при этом возрастает. Если сила совершает отрицательную работу, то кинетическая энергия тела уменьшается. Это происходит, например, при уменьшении скорости тела при действии силы трения. Кинетическая энергия измеряется в тех же единицах, что и работа, т. е. в джоулях. Так же как и в том случае, когда тело обладает потенциальной энергией, работа может быть совершена за счет кинетической энергии. При совершении работы происходит изменение положения тела и изменение его энергии. 2. Деформации. Напряжения. Закон Гука. Деформация - это изменение формы и размеров тела под действием внешних сил, при изменении температуры, влажности, фазовых превращениях и других воздействиях, вызывающих изменение положения частиц тела. При увеличении напряжения деформация может закончиться разрушением. Деформации бывают разных видов: растяжения, сжатия, сдвига, изгиба, кручения. Все перечисленные виды деформации возможны в твердых телах. В жидкостях и газах возможны только деформации объемного сжатия и растяжения, т. к. эти среды не обладают упругостью формы, а только объема. Напряжение — это сила, действующая на единицу площади поперечного сечения материала. Напряжение, действующее на некоторую площадку любой поверхности внутри тела, можно разложить на две компоненты: нормальное напряжение, направленное перпендикулярно этой площадке, и сдвиговое, лежащее в плоскости площадки. В любой точке находящегося в напряженном состоянии тела можно выделить три ортогональные плоскости, на которых напряжения полностью являются нормальными, т. е. вдоль них не действуют сдвиговые напряжения. Эти плоскости определяют три ортогональные оси, называемые главными осями напряжений, а нормальные напряжения, действующие в этих направлениях, называются главными напряжениями. Каждое главное напряжение отражает равновесие равных, но противоположно направленных компонент сил. Напряжение считается сжимающим, если силы направлены навстречу друг другу, и растягивающим, если они направлены в противоположные стороны. Если внутри тела все главные напряжения равны по величине, то режим напряжений называют гидростатическим, поскольку таким является напряженное состояние всего объема жидкости, находящегося в покое. В гидростатическом поле напряжений не существует сдвиговых напряжений, так как они не могут поддерживаться в жидком теле. Если главные напряжения не равны, сдвиговые напряжения действуют вдоль всех поверхностей внутри напряженного тела, за исключением трех ортогональных плоскостей, пересекающихся по главным осям. Тело, подвергающееся действию напряжений, испытывает изменение формы и (или) размеров, называемое деформацией. Вплоть до некоторого предельного значения напряжения, называемого пределом текучести материала, величина деформации изменяется пропорционально приложенному напряжению (закон Гука). Эта упругая деформация является обратимой, т.е. снятие напряжения ведет к снятию деформации. Если напряжение превысит предел текучести, деформация становится нелинейной и частично необратимой и называется она пластической деформацией. Если напряжение возрастает еще больше, тело разрушается. F = –kx | Билет №12 1. Теорема Кенига. Теорема Кёнига позволяет выразить полную кинетическую энергию механической системы через энергию движения центра масс и энергию движения относительно центра масс. Кинетическая энергия механической системы есть энергия движения центра масс плюс энергия движения относительно центра масс Где Т-полная кинетическая энергия системы, Т0 – кинетическая энергия движения центра масс, Тr – относительная кинетическая энергия системы. Иными словами, полная кинетическая энергия тела или системы тел в сложном движении равна сумме энергии системы в поступательном движении и энергии системы в её движении относительно центра масс. Более точная формулировка: Кинетическая энергия системы материальных точек равна сумме кинетической энергии всей массы системы, мысленно сосредоточенной в её центре масс и движущейся вместе с ним, и кинетической энергии той же системы в её относительном движении по отношению к поступательно движущейся системе координат с началом в центре масс. 2. Движение относительно неинерциальных систем отсчета. Поскольку любая не инерциальная система отсчета движется относительно инерциальных систем с некоторым ускорением, ускорение тела в неинерциальной системе отсчета w' будет отлично от w. Если неинерциальная система движется относительно инерциальной поступательно, то а совпадает ускорением неинерциальной системы отсчета. При вращательном движении различные точки неинерциальной системы имеют неодинаковое ускорение. В этом случае нельзя трактовать как ускорение, с которым неинерциальная система движется относительно инерциальной. Пусть результирующая всех сил, обусловленных действием на данное тело со стороны других тел, равна. Тогда согласно второму закону Ньютона | ||||
| Билет № 1 1. Гармонические колебания физического маятника. При небольших углах отклонения α физический маятник так же совершает гармонические колебания. Будем считать, что вес физического маятника приложен к его центру тяжести в точке С. Силой, которая возвращает маятник в положение равновесия, в данном случае будет составляющая силы тяжести – сила F. Знак минус в правой части означает то, что сила F направлена в сторону уменьшения угла α. С учетом малости угла α Для вывода закона движения математического и физического маятников используем основное уравнение динамики вращательного движения
Решение этого уравнения 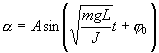 Определим длину l математического маятника, при которой период его колебаний равен периоду колебаний физического маятника, т.е. Из этого соотношения определяем Данная формула определяет приведенную длину физического маятника, т.е. длину такого математического маятника, период колебаний которого равен периоду колебаний данного физического маятника. 2. Мгновенная ось вращения. Мгновенная ось вращения — геометрическое место точек, скорость которых в данный момент времени равна нулю. Мгновенная ось вращения — ось бесконечно малого поворота тела, определяется из уравнения: где М — произвольная точка, лежащая на оси вращения. Уравнения мгновенной оси в неподвижной системе координат можно записать в виде 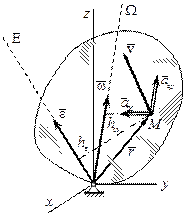 Скорость и ускорение точки при сферическом движении твердого тела Перемещаясь в пространстве и внутри тела, Мгновенная ось опишет собой конические поверхности, которые называются соответственно неподвижным и подвижным аксоидами. Для получения уравнений этих поверхностей необходимо из уравнений мгновенной оси вращения исключить время. Подвижный аксоид катится без проскальзывания по неподвижному. Данный вывод следует из равенства нулю скоростей точек мгновенной оси вращения, которая является в текущий момент общей для неподвижного и подвижного аксоидов. | Билет № 2 1. Уравнение моментов относительно движущегося начала и движущейся оси. Уравнение моментов относительно движущегося начала и движущейся оси. Уравнение моментов может быть записано не только относительно неподвижной точки, но и относительно любой точки, движущейся с постоянной скоростью в силу равноправия всех ИСО. Точку приложения любой силы можно перемещать по прямой, на которой лежит эта сила. При действии на тело нескольких параллельных сил их можно заменить равнодействующей, приложенной к такой точке, чтобы момент равнодействующей = сумме моментов действующих сил: 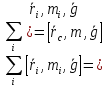 , С – точка, к которой приложена равнодействующая. , С – точка, к которой приложена равнодействующая.В однородном поле силы тяжести точка приложения равнодействующей совпадает с центром масс. Если гравитационное поле неоднородно, то положение центра масс и центра тяжести не совпадает. Пусть точка А, относительно которой будет вычисляться момент импульса и сил, движется с произвольной скоростью 2. Вынужденные колебания. Резонанс Вынужденные колебания – это колебания, происходящие под действием внешней периодически действующей силы. В отличие от свободных колебаний, когда система получает энергию лишь один раз (при выведении системы из состояния равновесия), в случае вынужденных колебаний система поглощает эту энергию от источника внешней периодической силы непрерывно. Эта энергия восполняет потери, расходуемые на преодоление трения, и потому полная энергия колебательной системы no-прежнему остается неизменной. Вынужденные колебания в отличие от свободных могут происходить с любой частотой. Частота вынужденных колебаний совпадает с частотой внешней силы, действующей на колебательную систему. Таким образом, частота вынужденных колебаний определяется не свойствами самой системы, а частотой внешнего воздействия. Примерами вынужденных колебаний являются колебания детских качелей, колебания иглы в швейной машине, поршня в цилиндре автомобильного двигателя, рессор автомобиля, движущегося по неровной дороге и т.д. Резонанс – это явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к собственной частоте колебательной системы. Резонанс возникает из-за того, что при 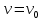 внешняя сила, действуя в такт со свободными колебаниями, все время имеет одинаковое направление со скоростью колеблющегося тела и совершает положительную работу: энергия колеблющегося тела увеличивается, и амплитуда его колебаний становится большой. Если же внешняя сила действует «не в такт», то эта силы попеременно совершает то отрицательную, то положительную работу и вследствие этого энергия системы меняется незначительно. внешняя сила, действуя в такт со свободными колебаниями, все время имеет одинаковое направление со скоростью колеблющегося тела и совершает положительную работу: энергия колеблющегося тела увеличивается, и амплитуда его колебаний становится большой. Если же внешняя сила действует «не в такт», то эта силы попеременно совершает то отрицательную, то положительную работу и вследствие этого энергия системы меняется незначительно.С явлением резонанса мы часто встречаемся в повседневной жизни. Если в комнате задрожали стекла при прохождении по улице тяжелого грузовика, это значит, что собственная частота колебаний стекол равна частоте колебаний машины. Если морские волны попадают в резонанс с периодом корабля, то качка становится особенно сильной. Явление резонанса необходимо учитывать при проектировании мостов, зданий и других сооружений, испытывающих вибрацию под нагрузкой, в противном случае при определенных условиях эти сооружения могут быть разрушены. Однако резонанс также может быть полезен. Явление резонанса используется при настройке радиоприемника на определенную частоту радиовещания, а также во многих других случаях. | ||||
| Билет № 3 1. Скорость и ускорение. скорость – векторная физическая величина, равная отношению вектора перемещения к промежутку времени, за которое оно произошло А теперь представим, что промежуток времени уменьшается, уменьшается, и становится совсем коротким, стремится к нулю. В таком случае о средней скорости говорить на приходится, скорость становится мгновенной. Те, кто помнит основы математического анализа, тут же поймут, что в дальнейшем нам не обойтись без производной. Мгновенная скорость – векторная физическая величина, равная производной от радиус вектора по времени. Мгновенная скорость всегда направлена по касательной к траектории. В системе СИ скорость измеряется в метрах в секунду Если тело движется не равномерно и прямолинейно, то у него есть не только скорость, но и ускорение. Ускорение (или мгновенное ускорение) – векторная физическая величина, вторая производная от радиус-вектора по времени, и, соответственно, первая производная от мгновенной скорости Ускорение показывает, как быстро изменяется скорость тела. В случае прямолинейного движения, направления векторов скорости и ускорения совпадают. В случае же криволинейного движения, вектор ускорения можно разложить на две составляющие: ускорение тангенциальное, и ускорение нормальное. Тангенциальное ускорение показывает, как быстро изменяется скорость тела по модулю и направлено по касательной к траектории Нормальное же ускорение характеризует быстроту изменения скорости по направлению. Векторы нормального и тангенциального ускорения взаимно перпендикулярны, а вектор нормального ускорения направлен к центру окружности, по которой движется точка. Здесь R – радиус окружности, по которой движется тело. 2. Уравнение Бернулли. Формула Торричелли. Уравнение Бернулли является основным уравнением, описывающим движение идеальной несжимаемой жидкости. С формальной точки зрения уравнение Бернулли выражает закон сохранения энергии для жидкости в трубке тока. Оно может быть использовано и для газа при условии, что его давление, а значит и объем, изменяются достаточно слабо, и можно пренебречь изменением плотности. Выберем в стационарно текущей жидкости трубку тока небольшого диаметра так, чтобы физические величины, используемые в дальнейшем, можно было бы считать постоянными. Предположим, что два ее поперечных сечения, ориентированных перпендикулярно линиям тока, находятся на различной высоте h1 и h2 над исходным (нулевым) уровнем и имеют площади S1 и S2; скорости течения жидкости в этих сечениях равны, соответственно, υ1 и υ2. Пусть за время dt через сечение S1 в трубку втекает объем жидкости dW1=S1dL1, где dL1= V1dt. За это же время через сечение S2 вытекает объем dW2=S2V2dt. Из условия неразрывности струи следует: dW1= dW2. Движение жидкости в трубке тока выглядит так, как если бы элементарный объем жидкости dW1 из положения I переместился в положение II. 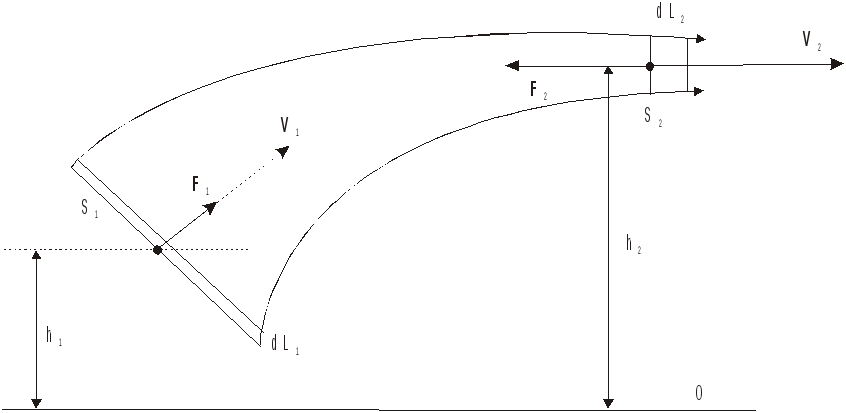 Е полной механической энергии объема dW:Найдем изменение где: Поскольку движение происходит в поле тяжести, трение отсутствует, а силы давления на боковую поверхность трубки тока работы не совершают, то изменение энергии объема жидкости вызвано только работой сил давления на основания трубки тока S1 и S2: Сила давления F1 совершает за время dt элементарную работу по перемещению элементарного объема dWI: dА1=F1dl1=P1S1V1dt. Аналогичным образом вычислим работу силы F2 в сечении S2. dA2= – F2dl2= – F2V2dt. Работа силы F2 отрицательна, так как направления вектора скорости V2 и силы давления F2 противоположны. Результирующая работа сил давления, по перемещению жидкости равна: Подставляя (9.4) и (9.6) в формулу (9.5) и перегруппировав члены, находим: Это и есть уравнение Бернулли. Поскольку выбор положений 1 и 2 сделан произвольно, то полученное соотношение имеет общий характер: величина имеет одно и тоже значение в любом сечении трубки тока. Все члены в правой части уравнения имеют размерность давления и представляют собой статическое, гидростатическое и динамическое давления. С помощью уравнения Бернулли легко получить некоторые важные результаты, как для движущейся жидкости, так и для жидкости, находящейся в равновесии. 9.3. Формула Торричелли Формулой Торричелли называют формулу, определяющую скорость V вытекания струи из отверстия. Рассмотрим резервуар в боковой стенке которого на глубине h от свободной поверхности жидкости имеется малое отверстие, через которое вытекает жидкость. Пусть свободной поверхности жидкости соответствует сечение S1, статическое давление на нее p1 равно атмосферному давлению pA. За счет вытекания жидкости из отверстия в стенке резервуара ее верхний уровень понижается. Если площадь S2 отверстия в сосуде достаточно мала, то скорость V1, с которой будет снижаться уровень свободной поверхности, также будет мала, и можно положить V1=0. Очевидно, что статическое давление в плоскости сечения S2 равно атмосферному давлению, т. е. р2=рА. Запишем уравнение Бернулли для сечений S1 и S2: Используя введенные выше обозначения и обозначив разность уровней h2-h1 через h, приходим к выражению: Решая уравнение относительно V, находим +Отметим, что скорость вытекания жидкости из отверстия на глубине h равна конечной скорости тела, свободно падающего с высоты h, и не зависит от направления вектора скорости V потока. |
