|
|
механика. Билет 7 Законы трения
υ1=√gRз=8 км/с
Вторая космическая скорость
Если тело обладает скоростью υ1υ1, то впоследствии при движении не упадет. Но значения
υ1υ1 недостаточно для выхода из сферы земного притяжения, то есть удалиться от Земли на расстояние, при котором оно теряет свою силу. Для этого нужна скорость υxυx, которая получила название второй космической или скорость убегания.
Третья космическая скорость
Для выхода за пределы Солнечной системы телу следует преодолеть как силу притяжения к Земле, так и к Солнцу. Для этого применяется третья космическая скорость υ3υ3, позволяющая запускать тело с земной поверхности
Билет № 20
1. Кинематика материальной точки. Линейные характеристики движения
В кинематике рассматривается механическое движение без выяснения причин, его вызывающих. Механическое движение – изменение положения тела в пространстве относительно других тел с течением времени. При изучения механического движения реальных объектов в физике используются физические модели, такие как материальная точка, система материальных точек, абсолютно твердое тело, сплошная среда. Материальная точка – тело, размерами и формой которого можно пренебречь в условиях данной задачи. Тело можно рассматривать как материальную точку, если его размеры малы по сравнению с расстоянием, которое оно проходит, или по сравнению с расстояниями от него до других тел. Траектория – линия, вдоль которой материальная точка движется в пространстве в выбранной системе отсчета. По форме траектории движение можно разделить на прямолинейное и криволинейное. Для характеристики положения материальной точки используют радиус-вектор. Расстояние S, отсчитанное по траектории называется длиной пути AB=S. Вектор, соединяющий начальную и конечную точки траектории называется перемещением. Движение тела, при котором все его точки в данный момент времени движутся одинаково, называется поступательным движением. Для описания поступательного движения достаточно выбрать одну точку и описать ее движение. Движение, при котором траектории всех точек тела являются окружностями с центрами на одной прямой и все плоскости окружностей перпендикулярны этой прямой, называется вращательным движением. Абсолютно твердое тело – тело, размеры и форма которого не меняются в процессе движения. Чтобы описать механическое движение тела, нужно знать его координаты в любой момент времени. Для определения координат материальной точки следует выбрать тело отсчета и связать с ним систему координат. Система координат, тело отсчета, с которым она связана, и указание начала отсчета времени образуют систему отсчета, относительно которой рассматривается движение тела. Для описания многих движений систему отсчета связывают с Землей, считая ее неподвижной. В ряде случаев в качестве тела отсчета выбирают Солнце или отдаленные звезды. Траектория движения тела, пройденный путь и перемещение зависят от выбора системы отсчета. Другими словами, механическое движение относительно. Основными кинематическими характеристиками движения материальной точки являются скорость и ускорение.
Линейные характеристики описывают движение любой точки тела вдоль траектории, являющейся окружностью. К ним относятся:
• перемещение;
• путь;
• линейная скорость:
V = ώr,
где, r – радиус окружности;
• линейное ускорение, м /с ²:
а = εr
При вращении твёрдого тела относительно оси линейные скорости точек тела, лежащих на разных расстояниях от оси вращения различны, в то время, как угловая скорость всех его точек одинакова.
2. Примеры расчета потенциальной энергии для различных взаимодействий.
Потенциальная энергия тела массой т на высотеh
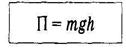 Это выражение вытекает из того, что потенциальная энергия равна работе силы тяжести при падении тела с высоты h на поверхность Земли. Это выражение вытекает из того, что потенциальная энергия равна работе силы тяжести при падении тела с высоты h на поверхность Земли.
Высота h отсчитывается от нулевого уровня, для которого П0 = 0, g — ускорение свободного падения.
Поскольку начало отсчета выбирается произвольно, то потенциальная энергия может иметь отрицательное значение (кинетическая энергия всегда положительна!). Если принять за нуль потенциальную энергию тела, лежащего на поверхности Земли, то потенциальная энергия тела, находящегося на дне шахты (глубина Л'), П = -mgh'.
Потенциальная энергия упруго деформированного тела (пружины)
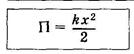 Это выражение получается из того, что работа силы при деформации пружины идет на увеличение потенциальной энергии пружины. Это выражение получается из того, что работа силы при деформации пружины идет на увеличение потенциальной энергии пружины.
Элементарная работа dA, совершаемая силой Fx при бесконечно малой деформации dx, dA = Fx dx = kx dx (Fx = -F x упр = -(-kx) = kx).
Полная работа 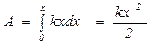 . .
[k — коэффициент упругости (для пружины — жесткость); Fх упр =- kx - проекция силы упругости на ось х; Fх упр направлена в сторону, противоположную деформации x. По третьему закону Ньютона деформирующая сила равна по модулю силе упругости и противоположно ей направлена]
Полная механическая энергия системы___ 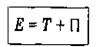 Энергия механического движения и взаимодействия, т. е. равна сумме кинетической и потенциальной энергий. Энергия механического движения и взаимодействия, т. е. равна сумме кинетической и потенциальной энергий.
|
Билет № 17
1. Закон сохранения момента импульса.
Импульс – это величина, подчиняющаяся Законам сохранения. Для вращательного движения Закон также остается в силе. Закон сохранения момента импульса гласит:
Для замкнутой системы суммарный момент импульсов всех материальных точек остается постоянным во времени.
То есть, также, как и для поступательного движения, момент импульса системы может изменяться только лишь при внешнем воздействии на нее.
Вне этих воздействий могут меняться составляющие момента импульса, но не сам момент импульса. Например, при упругом столкновении двух материальных точек равной массы, они могут полностью изменить направление вращения, и, таким образом, момент импульса каждой поменяет знак. Однако, если суммарный момент импульса этих двух точек был нулевой, то и после столкновения он останется нулевым.
Вращение любого тела рано или поздно прекращается в результате трения. Однако, Закон сохранения момента импульса здесь не нарушается, поскольку система не замкнута. Момент импульса уменьшается за счет того, что энергия вращающегося тела уходит, превращаясь во внутреннюю энергию трущихся поверхностей.
Закон сохранения момента импульса, также, как и Закон сохранения импульса для поступательного движения – это следствие симметрии пространства, то есть, равноправия всех точек пространства для физических законов.
2. Твердое тело в механике. Уравнения движения и равновесия твердого тела
Так как твердое тело является механической системой с шестью степенями свободы, то для описания его движения требуется шесть независимых числовых уравнений или два независимых векторных уравнения.
Одно из них – это уравнение движения центра масс С
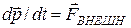 , где , где 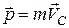 . (1) . (1)
Второе – уравнение моментов
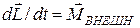 . (2) . (2)
Если твердое тело покоится, то уравнения (1) и (2) переходят в
 . (3) . (3)
Это необходимые условия равновесия твердого тела. Но они не являются достаточными. При их выполнении центр масс может двигаться прямолинейно и равномерно с произвольной скоростью, а само тело может вращаться с сохранением момента импульса. Такое движение твердого тела называют свободным. Следует отметить, что даже свободное движение твердого тела может быть очень сложным. Поэтому сначала рассмотрим простейший случай движения твердого тела.
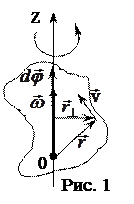
Вращение твердого тела вокруг неподвижной оси
Движение твердого тела, при котором все точки прямой АВ, жестко связанной с телом, остаются неподвижными, называется вращением тела вокруг неподвижной оси АВ.
Такое твердое тело имеет одну степень свободы и его положение в пространстве полностью определяется значением угла поворота вокруг оси вращения из некоторого, условно выбранного, начального положения этого тела. Мерой перемещения тела за малый промежуток времени dt полагают вектор 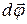 элементарного поворота тела. По модулю он равен углу поворота тела за время dt, а его направление совпадает с направлением поступательного движения правого буравчика, направление вращения рукоятки которого совпадает с направлением вращения тела. Вектор угловой скорости элементарного поворота тела. По модулю он равен углу поворота тела за время dt, а его направление совпадает с направлением поступательного движения правого буравчика, направление вращения рукоятки которого совпадает с направлением вращения тела. Вектор угловой скорости 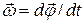 . .
Если 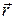 – радиус вектор, проведенный из некоторой точки О на оси вращения ОZ до произвольной материальной точки тела, то скорость этой точки определяется соотношением – радиус вектор, проведенный из некоторой точки О на оси вращения ОZ до произвольной материальной точки тела, то скорость этой точки определяется соотношением 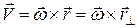 , (5) , (5)
где 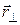 – составляющая вектора – составляющая вектора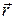 , перпендикулярная оси, т.е. , перпендикулярная оси, т.е. 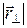 – кратчайшее расстояние от оси до материальной точки. – кратчайшее расстояние от оси до материальной точки.
Уравнение динамики тела, вращающегося вокруг неподвижной оси z, имеет вид
 dLz/dt = MzВНЕШН, (6) dLz/dt = MzВНЕШН, (6)
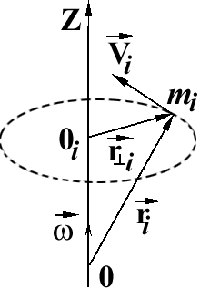 где где 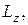 MzВНЕШН – проекции моментов импульса MzВНЕШН – проекции моментов импульса 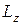 и момента силы MzВНЕШН на ось вращения z. Выведем другое выражение для уравнения (6). Определим момент импульса относительно точки О, лежащей на оси ОZ (см. рис. 2), полагая и момента силы MzВНЕШН на ось вращения z. Выведем другое выражение для уравнения (6). Определим момент импульса относительно точки О, лежащей на оси ОZ (см. рис. 2), полагая 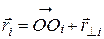 , где , где 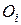 – центр окружности, по которой движется i-я материальная точка твердого тела, тогда – центр окружности, по которой движется i-я материальная точка твердого тела, тогда
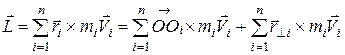 . .
Первое слагаемое перпендикулярно оси ОZ, а второе параллельно, так как 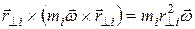 . .
Таким образом 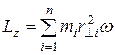 или или 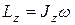 , (7) , (7)
где величина
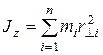 (8) (8)
называется моментом инерции тела относительно оси Z .
Тогда уравнение динамики тела, вращающегося относительно неподвижной оси Z [см. (6)], можно записать в виде 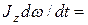 MzВНЕШН или MzВНЕШН или 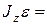 MzВНЕШН. MzВНЕШН.
|
Билет № 14
1. Закон сохранения и изменения механической энергии. Силы и потенциальная энергия.
Изменение полной механической энергии системы тел происходит при совершении работы силами, действующими как между телами системы, так и со стороны внешних тел.
Изменение механической энергии ∆E системы тел определяется законом изменения полной механической энергии:
∆E = E2 − E1 = Aвнеш + Aтр(сопр),
где E1 — полная механическая энергия начального состояния системы; E2 — полная механическая энергия конечного состояния системы; Aвнеш — работа, совершаемая над телами системы внешними силами; Aтр(сопр) — работа, совершаемая силами трения (сопротивления), действующими внутри системы.
В механике все силы делятся на две группы: консервативные и неконсервативные.
Консервативные силы
Консервативными, или потенциальными, называются такие силы, работа которых не зависит от траектории, а определяется только начальным и конечным положениями тела. Работа таких сил по перемещению тела по замкнутой траектории всегда равна нулю. Примеры потенциальных (консервативных) сил:
· сила тяжести
· сила упругости
· гравитационная сила
Неконсервативные силы
Неконсервативными называются такие силы, работа которых зависит от траектории. Сама сила в этом случае зависит от модуля и направления вектора скорости. Работа таких сил может приводить к выделению тепла — часть механической энергии при этом превращается в тепловую. Примеры неконсервативных сил:
· сила упругости
· сила сопротивления среды
2. Законы Кеплера и закон всемирного тяготения.
Первый закон Кеплера
Планеты Солнечной системы движутся по эллиптическим орбитам. В одном из фокусов такой орбиты находится Солнце.
Второй закон Кеплера, или закон площадей
Радиус-вектор планеты описывает в равные промежутки времени равные площади.
Третий закон Кеплера
Квадраты периодов обращения планет относятся как кубы больших полуосей их орбит.
Таким обоснованием стало открытие закона всемирного тяготения Исааком Ньютоном:
Определение 4
Закон всемирного тяготения:
F=GMmr2F=GMmr2,
где MM и mm – массы Солнца и планеты, rr – расстояние между ними, G = 6,67⋅10–11 Н⋅м2/кг2G = 6,67·10–11 Н·м2/кг2 – гравитационная постоянная.
|
Билет № 16
1. Момент силы и момент импульса относительно неподвижного начала. Уравнение моментов.
Моме́нт и́мпульса (кинетический момент, угловой момент, орбитальный момент, момент количества движения) характеризует количество вращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение. Единицы измерения СИ - м2·кг·с−1 // джоуль-секунда; Дж·с. СГС - см2·г·с−1
Момент силы (синонимы: крутящий момент, вращательный момент, вертящий момент, вращающий момент) — векторная физическая величина, равная произведению радиус-вектора, проведенного от оси вращения к точке приложения силы, на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело. Единицы измерения СИ - Ньютон-метр
Уравнение моментов. Закон сохранения момента импульса.
Закон сохранения момента импульса (закон сохранения углового момента): векторная сумма всех моментов импульса относительно любой неподвижной точки (или сумма моментов относительно любой неподвижной оси) для замкнутой системы остается постоянной со временем.
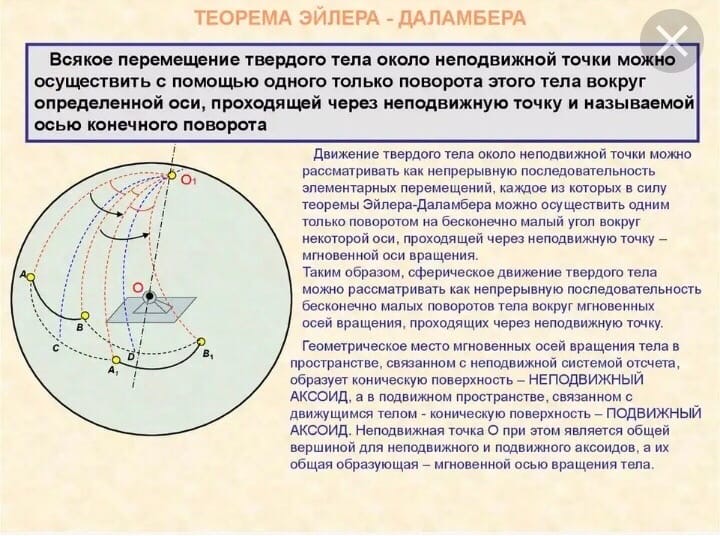
2. Теорема Эйлера. Общее движение твердого тела.
|
|
|
|
 Скачать 1.1 Mb.
Скачать 1.1 Mb.