механика. Билет 7 Законы трения

• Название: Билет 7 Законы трения
• Анкор: механика
• Дата: 25.03.2023
• Размер: 1.1 Mb.
• Имя файла: Dlya_zacheta_po_mekhanike.docx
• Тип: Закон; #1013993
• страница: 4 из 5

Третий закон Ньютона

Этот закон объясняет, что происходит с двумя материальными точками. Возьмём для примера замкнутую систему, состоящую из двух материальных точек. Первая точка может действовать на вторую с некоторой силой  , а вторая — на первую с силой  . Как соотносятся силы? Третий закон Ньютона утверждает: сила действия равна по модулю и противоположна по направлению силе противодействия. Подчеркнём, что эти силы приложены к разным материальным точкам, а потому вовсе не компенсируются.

Современная формулировка

Материальные точки взаимодействуют друг с другом силами, имеющими одинаковую природу, направленными вдоль прямой, соединяющей эти точки, равными по модулю и противоположными по направлению:



Закон отражает принцип парного взаимодействия.

2. Гидростатика сжимаемой жидкости. Барометрическая формула

Несжимаемые жидкости и газы. В отличие от твердых тел газы и жидкости не обладают постоянством формы. Они обладают лишь объемной упругостью. Сжимаемость жидкостей очень мала, и в подавляющем большинстве явлений жидкости можно считать практически несжимаемыми. Газы же сжимаются легче, и в большинстве явлений их сжимаемость проявляется отчетливо.

В настоящем разделе мы ограничимся таким кругом явлений, в которых эффекты сжимаемости настолько незначительны, что ими можно пренебречь.

Основными величинами, определяющими состояние несжимаемой жидкости, являются давление  p, плотность жидкости r и ее объем V.

Давление P определяется силой нормального напряжения, p =   . Единица давления в СИ - паскаль, 1 Па = 1 Н/м². Кроме того, используются кратные единицы: гектопаскаль: 1 гПа = 100 Па, килопаскаль: 1 кПа = 1000 Па, и т.д. Плотность вещества r определяется отношением массы вещества к объему, который она занимает, r =   .

Для измерения плотности жидкостей используются ареометры. Давление в жидкостях и газах измеряется манометрами.

Закон Архимеда был открыт в 3-м веке до н.э. В современной формулировке он гласит:

На всякое тело, погруженное в жидкость, (или газ) действует со стороны этой жидкости (или газа) выталкивающая сила, равная весу вытесненной этим телом жидкости.

Чтобы тело, погруженное в жидкость полностью или частично, находилось в равновесии, нужно, чтобы сумма сил, действующих на тело, была равной нулю.



Это условие плавания тел. В зависимости от формы плавающего тела и положения его центра тяжести равновесие может быть устойчивым, неустойчивым и безразличным (рис.90).

Точка приложения равнодействующей сил Архимеда называется центром плавучести

Барометрическая формула — зависимость давления или плотности газа от высоты в поле силы тяжести.

Для идеального газа, имеющего постоянную температуру   и находящегося в однородном поле тяжести (во всех точках его объёма ускорение свободного падения   одинаково), барометрическая формула имеет следующий вид:



где   — давление газа в слое, расположенном на высоте   ,   — давление на нулевом уровне (   ),   — молярная масса газа,   — универсальная газовая постоянная,   — абсолютная температура. Из барометрической формулы следует, что концентрация молекул   (или плотность газа) убывает с высотой по тому же закону:



где   — масса молекулы газа,   — постоянная Больцмана.

Барометрическая формула может быть получена из закона распределения молекул идеального газа по скоростям и координатам в потенциальном силовом поле (см. Статистика Максвелла — Больцмана). При этом должны выполняться два условия: постоянство температуры газа и однородность силового поля. Аналогичные условия могут выполняться и для мельчайших твёрдых частичек, взвешенных в жидкости или газе. Основываясь на этом, французский физик Ж. Перрен в 1908 году применил барометрическую формулу к распределению по высоте частичек эмульсии, что позволило ему непосредственно определить значение постоянной Больцмана.

Барометрическая формула показывает, что плотность газа уменьшается с высотой по экспоненциальному закону. Величина   , определяющая быстроту спада плотности, представляет собой отношение потенциальной энергии частиц к их средней кинетической энергии, пропорциональной   . Чем выше температура   , тем медленнее убывает плотность с высотой. С другой стороны, возрастание силы тяжести   (при неизменной температуре) приводит к значительно большему уплотнению нижних слоев и увеличению перепада (градиента) плотности. Действующая на частицы сила тяжести   может изменяться за счёт двух величин: ускорения   и массы частиц   .

Следовательно, в смеси газов, находящейся в поле тяжести, молекулы различной массы по-разному распределяются по высоте.

Реальное распределение давления и плотности воздуха в земной атмосфере не следует барометрической формуле, так как в пределах атмосферы температура и ускорение свободного падения меняются с высотой и географической широтой. Кроме того, атмосферное давление увеличивается с концентрацией в атмосфере паров воды.

Барометрическая формула лежит в основе барометрического нивелирования — метода определения разности высот   между двумя точками по измеряемому в этих точках давлению (   и   ). Поскольку атмосферное давление зависит от погоды, интервал времени между измерениями должен быть возможно меньшим, а пункты измерения располагаться не слишком далеко друг от друга. Барометрическая формула записывается в этом случае в виде:   (в м), где   — средняя температура слоя воздуха между точками измерения,   — температурный коэффициент объёмного расширения воздуха. Погрешность при расчётах по этой формуле не превышает 0,1—0,5 % от измеряемой высоты. Более точна формула Лапласа, учитывающая влияние влажности воздуха и изменение ускорения свободного падения.

Билет № 6

1. Принцип относительности Галилея.

Принцип относительности Галилея. Всякое механическое явление при одних и тех же начальных условиях протекает одинаково в любой инерциальной системе отсчёта.

Инвариантность законов механики. 

Принцип относительности Галилея означает, что законы механики одинаковы во всех инерциальных системах отсчёта. А именно, математическая форма второго и третьего законов Ньютона не меняется при переходе от одной инерциальной системы отсчёта к другой.

Скорость тела относительно неподвижной системы отсчёта есть скорость тела относительно движущейся системы отсчёта плюс скорость движущейся системы относительно неподвижной. Мы видим, таким образом, что закон сложения скоростей в механике является следствием преобразований Галилея.
2. Материальная точка. Описание движения.

Материальная точка – физическая модель тела, обладающего массой; размерами, формой, вращением и внутренней структурой которого можно пренебречь в условиях данной задачи. Положение материальной точки в пространстве определяется как положение геометрической точки.

Способы описания движения (векторный, координатный, естественный)

ВЕКТОРНЫЙ СПОСОБ ОПИСАНИЯ ДВИЖЕНИЯ Положение точки задается радиусом-вектором Радиус-вектор – вектор, проведенный из начала отсчета в данную точку.

Кинематическое уравнение движения или закон движения материальной точки:



Перемещение является приращением радиуса-вектора точки за рассматриваемый промежуток времени

Вектор мгновенной скорости направлен по касательной к траектории в сторону движения

Скорость показывает быстроту изменения положения радиус-вектора при движении материальной точки в пространстве

КООРДИНАТНЫЙ СПОСОБ ОПИСАНИЯ ДВИЖЕНИЯ

Этот способ применяют тогда, когда траектория точки известна заранее l(t)l Положение точки определятся дуговой координатой – расстоянием вдоль траектории от выбранного начала отсчета Движение точки определено, если известны 1. ее траектория, 2. начало отсчета, 3. положительное направление отсчета дуговой координаты 4. и закон движения точки

ЕСТЕСТВЕННЫЙ СПОСОБ ОПИСАНИЯ ДВИЖЕНИЯ

  – единичный вектор, связанный с движущейся точкой и направленный по касательной к траектории в сторону возрастания дуговой координаты dt/dl v

Билет № 9

1. Приведенная масса.

Приведённой массой называется такая условная масса, сосредоточенная в точке приведения, кинетическая энергия T_n которой равняется сумме  кинетических энергий тех звеньев, массы которых приводятся к этой точке. Используем равенство (9). Согласно этому приведённая масса равна

 (15)

где u_B – скорость точки приведения.

В случае, когда массы звеньев приводятся к звену, совершающему вращательное движение относительно стойки, удобно пользоваться понятием приведённого момента инерции I_n этих масс относительно оси вращения звена приведения.

2. Деформация сдвига

При деформации сдвига любая прямая, первоначально перпендикулярная к горизонтальным слоям, повернется на некоторый угол φ. Следовательно, отношение сдвига δа двух произвольно взятых слоев к расстоянию между этими слоями δb будет одинаково для любой пары слоев. Это отношение естественно взять в качестве характеристики деформации сдвига:

 (117)

Величина γназывается относительным сдвигом. В силу малости угла φ можно положить tgφ = φ. Следовательно, относительный сдвиг γоказывается равным углу сдвига φ. Опыт показывает, что относительный сдвиг пропорционален тангенциальному напряжению:

 (118)

Коэффициент G зависит только от свойств материала и называется модулем сдвига. Он равен такому тангенциальному напряжению, при котором угол сдвига оказался бы равным 45° (tgφ = 1), если бы при столь больших деформациях не был превзойден предел упругости.

Билет № 10

1. Движение тел переменной массы.

Движение тел с переменной массой–движение при котором тело может приобретать ускорение не за счёт внешних сил, а за счёт изменения массы.

Уравнение движения тел с переменной не содержат ничего принципиально нового по сравнению с законами Ньютона, и являются их следствиями. Но они представляют большой интерес в связи с ракетной техникой.

Реактивная сила – это сила упругости, действующая на тело со стороны отбрасываемых им масс.

Выведем уравнение движения материальной точки с переменной массой на примере движения ракеты. Пусть m(t)-масса ракеты в произвольный момент времени t, а v(t)-ее скорость в тот же момент. Импульс ракеты в этот момент будет mv. Спустя dt масса и скорость ракеты получат приращение dm и dv( dm-отрицательна). Импульс ракеты станет (m+dm)(v+dv). Сюда надо добавить импульс движения газов, образовавшихся за dt. Он равен dm_газv_газ –масса и скорость газа, образовавшихся за dt. Вычитая из суммарного импульса системы в момент t+dt импульс системы в момент t, найдем приращение этой величины за dt. Это приращение равно Fdt, где F – геометрическая сумма всех внешних сил, действующих на ракету.

(m+dm)(v+dv)+dm­_газv_газ-mv = Fdt

Время dt устремим к нулю. Поэтому, раскрывая скобки, отбрасываем dmdv. Далее dm+dm_газ=0 и v_отн=v_газ-v есть скорость истечения газов относительно ракеты. Тогда

mdv = v_отнdm + Fdt , деля на dt

m(dv/dt) =v_отн(dm/dt) + F (1)

Член v_отн(dm/dt) – реактивная сила . Уравнение (1)-уравнение Мещерского или уравнение движения точки с переменной массой.

2. Деформация растяжения-сжатия

Деформацией растяжения или сжатия называется деформация, связанная с относительным удлинением или укорочением деформируемого участка

Типы деформаций Среди многочисленного разнообразия возможных деформаций принято выделять однородное растяжение (сжатие), сдвиг, кручение, изгиб. Эти деформации наиболее просто поддаются анализу. В общем случае произвольный малый объем тела подвергается либо растяжению (сжатию), либо сдвигу, либо одновременному растяжению (сжатию) и сдвигу. Поэтому деформации растяжение (сжатие) и сдвиг принято называть элементарными. Деформация растяжения сжатия. Область деформации растяжениясжатия, в пределах которой выполняется соотношение ,  E   называется областью пропорциональности, а само соотношение называется законом Гука для деформации растяжения-сжатия. Постоянный коэффициент E имеет размерность H/м2 или Н/мм2 и называется модулем Юнга. Для стали предел пропорциональности n лежит близко к пределу упругости, но вообще они могут и не совпадать.

Билет № 13

1. Консервативные и неконсервативные силы. Потенциальная энергия.

Консервативными называют такие силы, работа которых на пути между двумя точками зависит не от формы пути, а только от положения этих точек. консервативные силы — такие силы, работа которых по любой замкнутой траектории равна 0. Примерами консервативных сил являются: сила тяжести, сила упругости. Примерами неконсервативных сил являются сила трения и сила сопротивления среды. Если на систему частиц действуют только консервативные силы, можно для нее ввести понятие потенциальной энергии. Какое-либо произвольное положение системы, характеризующееся заданием координат ее материальных точек, условно примем за нулевое. Работа, совершаемая консервативными силами при переходе системы из рассматриваемого положения в нулевое, равна потенциальной энергии системы в первом положении. Работа консервативных сил не зависит от пути перехода, а потому потенциальная энергия системы при фиксированном нулевом положении зависит только от координат материальных точек системы в рассматриваемом положении. Иными словами, потенциальная энергия U системы является функцией только ее координат. Работа любых консервативных сил А_конс всегда происходит за счет убыли потенциальной энергии, т. е. А_конс = U₁ – U₂ = -?U. Работа неконсервативных сил, в отличие от консервативных, зависит от формы пути. Неконсервативные силы могут совершать как положительную, так и отрицательную работу. К неконсервативным силам, совершающим отрицательную работу, относятся, например, силы трения и сопротивления при движении тела в жидкости или газе. Это обусловлено тем, что направление действия этих сил и направление перемещения тела противоположны

(dA_неконс = F_неконсdS= F_неконсdscos180° = -F_неконсds)

Потенциальная энергия - механическая энергия системы тел, определяемая их взаимным расположением и характером сил взаимодействия между ними.
Консервативные (потенциальные) силы - силы, работа которых определяется только начальным и конечным положением тела и не зависит от траектории движения тела. Работа консервативных сил на замкнутом участке равна нулю. (сила тяжести, сила упругости).
Неконсервативные силы - силы, работа которых зависит от траектории движения тела. (сила трения).
Тело, находящееся в поле потенциальных сил, обладает потенциальной энергией. Работа консервативных сил совершается за счет убыли потенциальной энергии: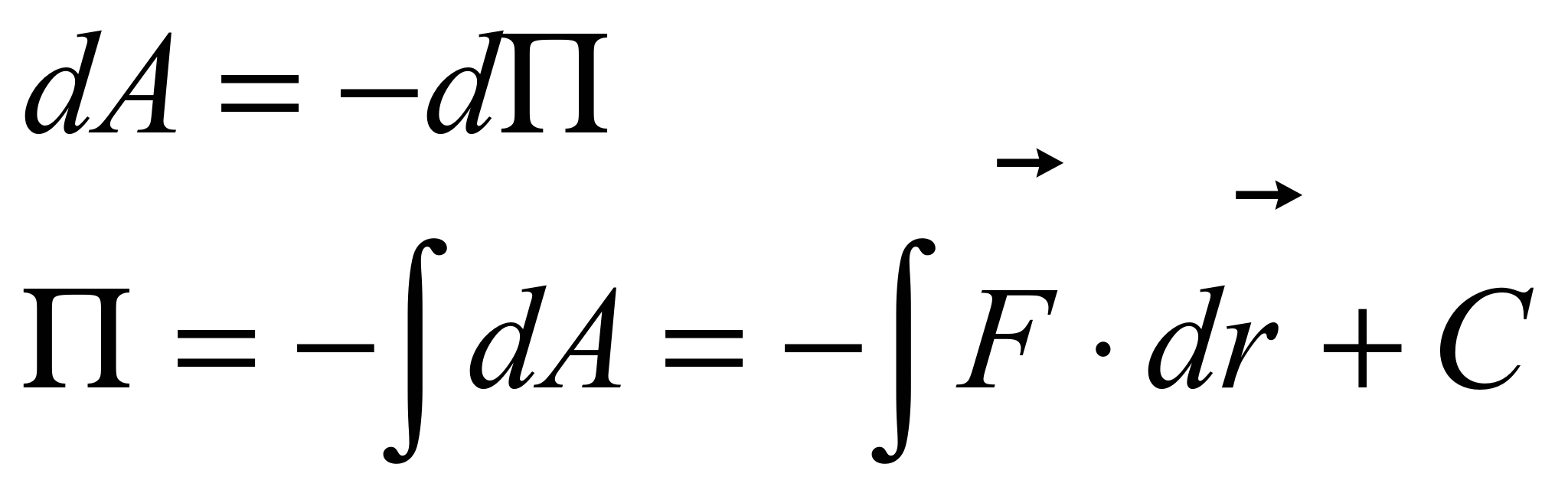

Потенциальная энергия определяется с точностью до постоянного множителя. Работа потенциальной силы равна разности значений потенциальной энергии в начальном и конечном состоянии.

Потенциальная энергия тела, поднятого над поверхностью Земли:

Потенциальная энергия упругодеформированного тела:

Потенциальная энергия является функцией состояния системы. Работа - это скалярная величина, которая определяется по формуле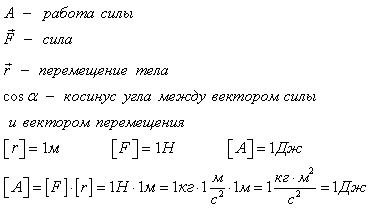

   

Работу выполняет не тело, а сила! Под действием этой силы тело совершает перемещение. Обратите внимание, что у работы и энергии одинаковые единицы измерения. Это означает, что работа может переходить в энергию. Например, для того, чтобы тело поднять на некоторую высоту, тогда оно будет обладать потенциальной энергией, необходима сила, которая совершит эту работу. Работа силы по поднятию перейдет в потенциальную энергию. Правило определения работы по графику зависимости F(r): работа численно равна площади фигуры под графиком зависимости силы от перемещения.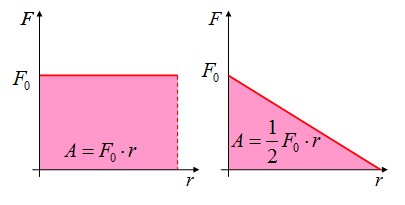



2. Условия эллиптического, параболического и гиперболического движений. Космические скорости.

 Когда траектория эллиптическая, движение планеты финитно , т. е. планета движется в ограниченной области пространства, не уходя в бесконечность. Напротив, в

случае гиперболических и параболических траекторий движение инфинитно — движение планеты не стеснено определенной областью пространства, она может удаляться в бесконечность. Таким образом, задача сводится, к нахождению условий финитности и инфинитности движения планеты.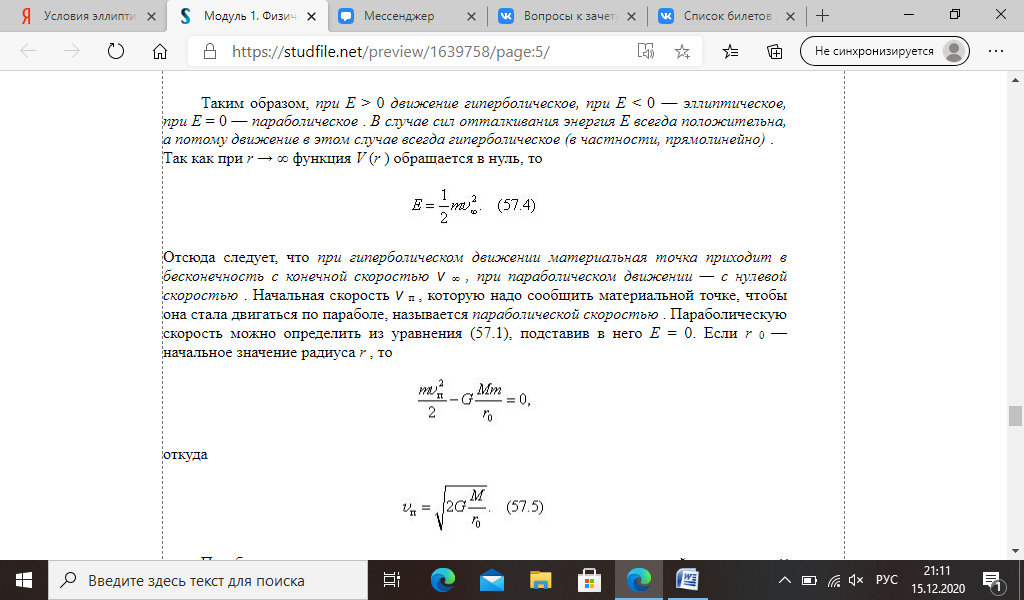





Первая космическая скорость
Для того, чтобы какое-либо тело могло стать спутником Земли, ему должна быть сообщена скорость υ1υ1, называемая первой космической. При подстановке значений gg и RзRз в формулу, получаем, что