14. Блочное программирование. Блочное программирование
 Скачать 0.6 Mb. Скачать 0.6 Mb.
|
|
Блочное прогр.doc Блочное программированиеИтак, мы достаточно подробно изучили симплекс-метод, двойственный симплекс-метод, а также модифицированный симплекс-метод. Что можно сказать об этих методах? Прежде всего, это - универсальные, конечные методы. Конечность - это гарантия решения задачи ЛП за конечное количество шагов (пусть и очень большое). Универсальность. Это означает, что данные методы практически не учитывают особенности строения матрицы коэффициентов ограничений. Главное, что задача относится к классу задач ЛП: <c,x> max , AX=A0 , x 0 . И вот здесь мы сталкиваемся с фундаментальным "законом" математического программирования: за универсальность нужно платить. Иными словами, конкретную задачу лучше, эффективнее решать методом, ориентированным на особенности именно этой задачи, чем методом, полностью игнорирующим любые особенности. Например, в нелинейном программировании вообще нет универсальных методов. Практически каждый метод (за исключением, разве что, полного перебора) предъявляет определенные требования, как к целевой функции, так и к функциям, определяющим множество допустимых решений1. Но вернемся к линейному программированию. Многие классы широко распространенных задач ЛП обладают специфическим строением матрицы ограничений (A) . Эти особенности позволяют существенно снизить трудоемкость решения данных задач. Первый из рассматриваемых нами классов представляют задачи так называемого "блочного программирования". Задачи блочного программированияНекоторые задачи ЛП большой размерности имеют такие структурные особенности, которые позволяют найти их оптимальное решение путем т.н. декомпозиции (или разложения) исходной задачи на ряд подзадач меньшей размерности. Причем эти подзадачи решаются практически независимо друг от друга. Основной эффект при таком подходе связан с тем, что существенно легче решить много "маленьких" задач, чем одну, но "большую". В математическом программировании это связано с полиномиальной и, даже, экспоненциальной зависимостью трудоемкости решения задач от их размерности. Преимущество методов, использующих "декомпозицию" исходной задачи на подзадачи меньшей размерности заключается в том, что с помощью этих методов оказывается возможным решение задач такой размерности, которые не удается решить другими методами из-за практически невыполнимого объема вычислений. Ситуации, приводящие к постановке подобных задач, встречаются довольно часто. Например, это - задачи планирования производственной деятельности предприятий, входящих в объединение. Хотя каждое из таких предприятий может иметь свои независимые ограничения, производственные программы отдельных предприятий обычно согласовывают на верхнем уровне управления из-за объективно существующих ограничений (связанных, например, с общим объемом финансовых ресурсов, которыми располагает объединение).  При этом возникает задача ЛП, обладающая структурой, которую в схематичной форме можно представить следующим образом.
Независимые ограничения
Что здесь интересно? Независимые ограничения имеют блочно-диагональную структуру. При отсутствии общих ограничений различные виды производств могут рассматриваться, как совершенно независимые. Поэтому нет проблем, если общие ограничения, образующие т.н. БЛОК-СВЯЗКУ, отсутствуют:
Независимые ограничения
Решить подобную задачу - это просто "разрезать" ее на L независимых задач, решить каждую из этих задач и объединить полученные оптимальные решения. При этом: Наличие же блока-связки, в общем случае, приводит к тому, что Теория блочного программирования ориентирована на решение методом декомпозиции задач, имеющих как общие, так и независимые ограничения. Класс задач с подобной структурой достаточно широк. В частности, к этому классу очень просто сводятся задачи, имеющие матрицу ограничений вида:  Ясно, что двойственная задача имеет блочно-диагональную структуру с блоком-связкой. Более того, при сильной разреженности матрицы ограничений можно (небезуспешно) попытаться путем перестановки строк и столбцов придать произвольной задаче подобную структуру. Метод декомпозиции Данцига-Вулфа: построение координирующей задачиРассмотрим некоторую задачу ЛП, имеющую блочно-диагональную структуру. Пусть задача имеет n переменных, пронумерованных числами натурального ряда: {1,2,...,n}. Множество индексов (номеров) переменных разобьем на L подмножеств по принципу принадлежности соответствующих переменных к 1-му, 2-му, ... , L-му диагональному блоку. 1={1, 2, ... ,q1}, 2={ q1+1, q1+2, ... ,q2}, ................................ ={ q - 1+1, q - 1+2, ... ,q}, ................................ L={ qL - 1+1, qL - 1+2, ... ,qL}. Здесь qL=n , q0=0. Такое разбиение позволяет записать задачу с блочно-диагональной структурой в следующем виде. 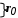 , ,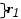 , , = =.  ........................................................................................... ............................................................................................  ........................................................................................... ........................................................................................... Здесь: Aj- Dj - вектор-столбец коэффициентов при переменной xj , принадлежащий диагональному блоку (если j ). Его размерность - Размерность этой задачи А теперь, запомнив формальную запись этой задачи, приступим к изложению общей идеи метода декомпозиции Данцига-Вулфа. Будем считать, что в задаче имеется один блок-связка AX=B0 и один-единственный диагональный блок DX=B*. Здесь B*= 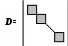 Теперь задачу можно записать следующим образом: 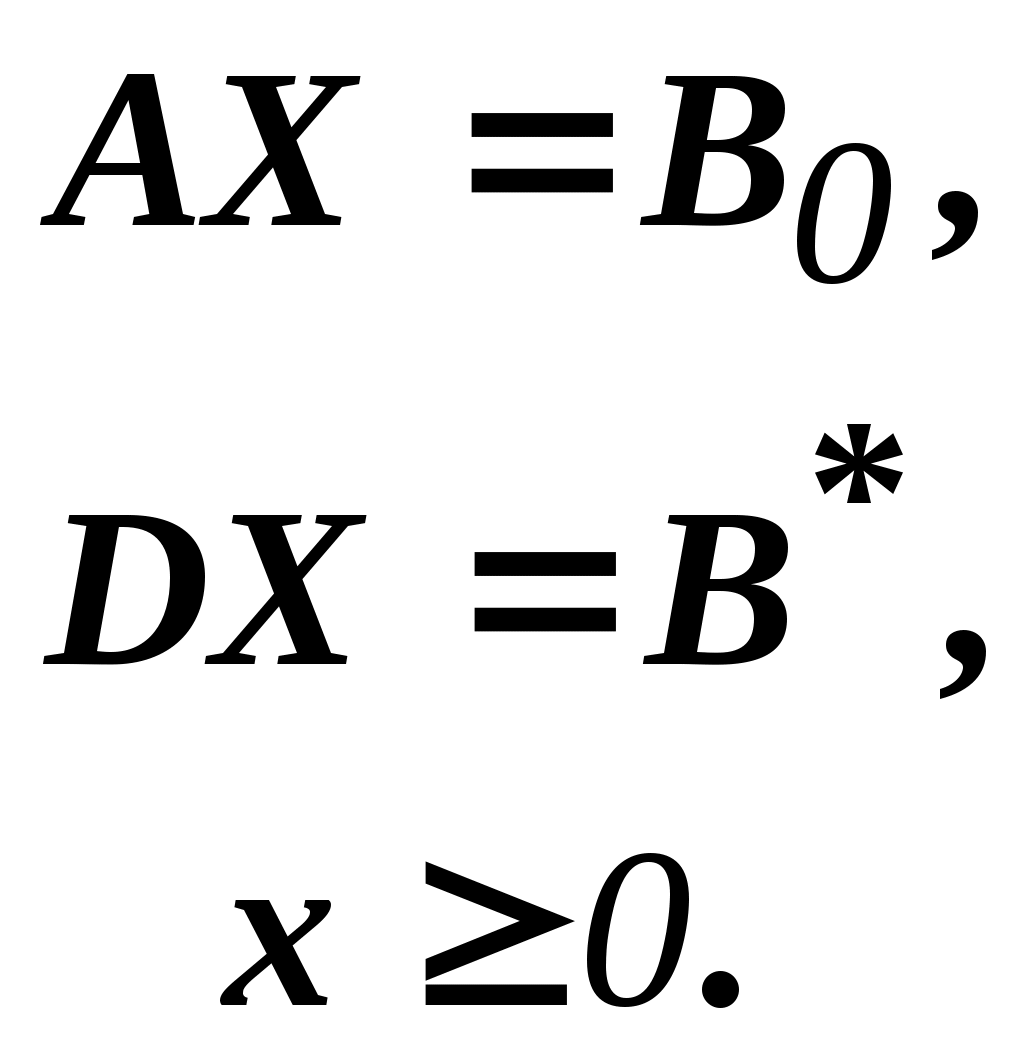 Казалось бы, здесь потеряна специфика блочно-диагональной структуры задачи. Позже будет показано, что это не так. Будем, для простоты, считать, что Как известно, любую точку ограниченного выпуклого множества можно представить, как выпуклую линейную комбинацию экстремальных точек (вершин). То есть, если Очевидно, что любая точка, представленная в виде (), удовлетворяет всем ограничениям 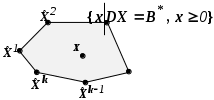 Здесь Это обстоятельство позволяет видоизменить исходную задачу таким образом, что из рассмотрения будут исключены все ограничения диагонального блока. Примем обозначения: А=(А1,А2, ... ,Аn) - матрица, составленная из векторов блока-связки. Теперь задача приобретает следующий вид: () 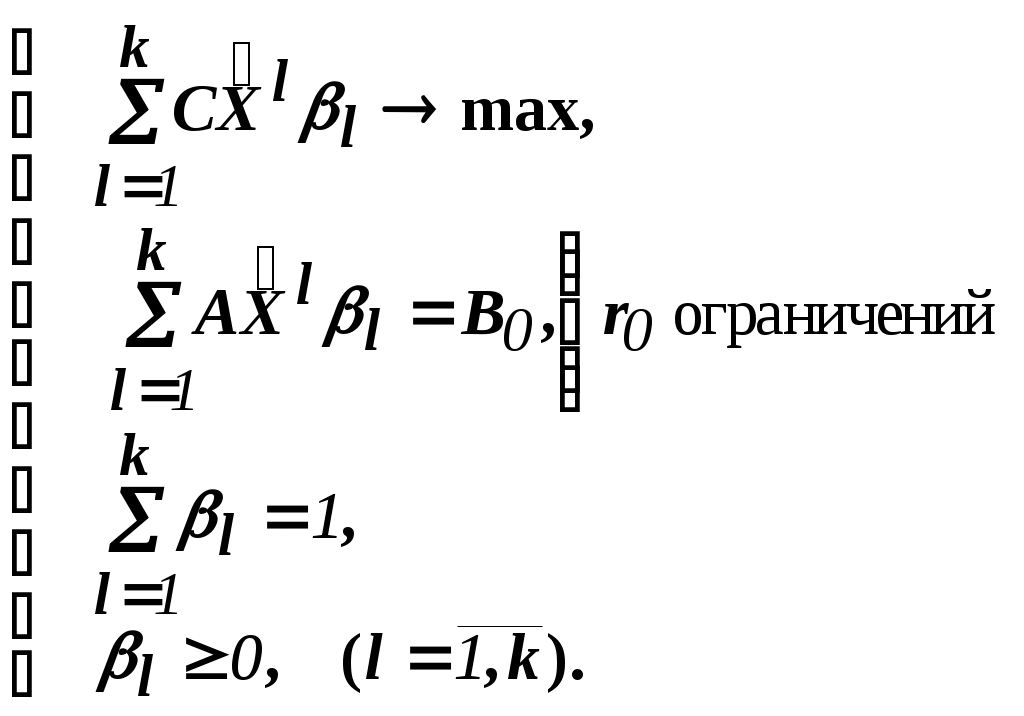  Как видно, все ограничения, составляющие диагональный блок Добавилось же только одно - Но в новой задаче появились новые переменные Там не менее ясно, что найдя значения этих переменных, можно найти и решение исходной задачи: Определение. Задачу, соответствующую этой новой формулировке () будем называть главной, или, что то же самое, координирующей задачей. Упростим обозначения: 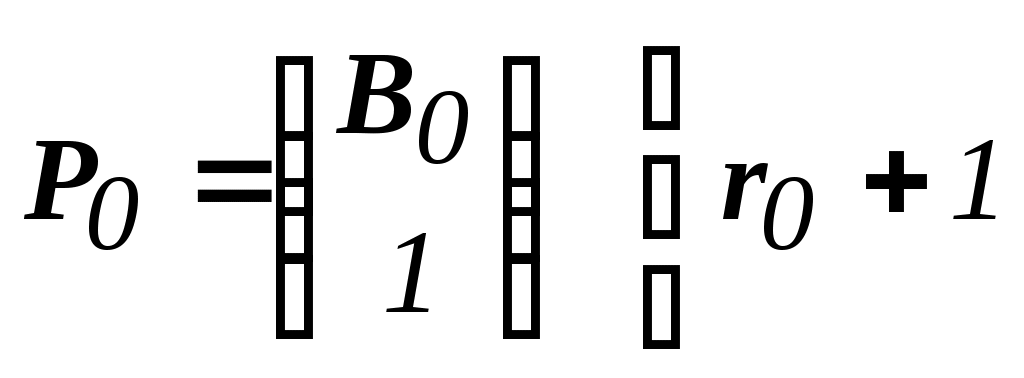 Пришли к следующей задаче: () 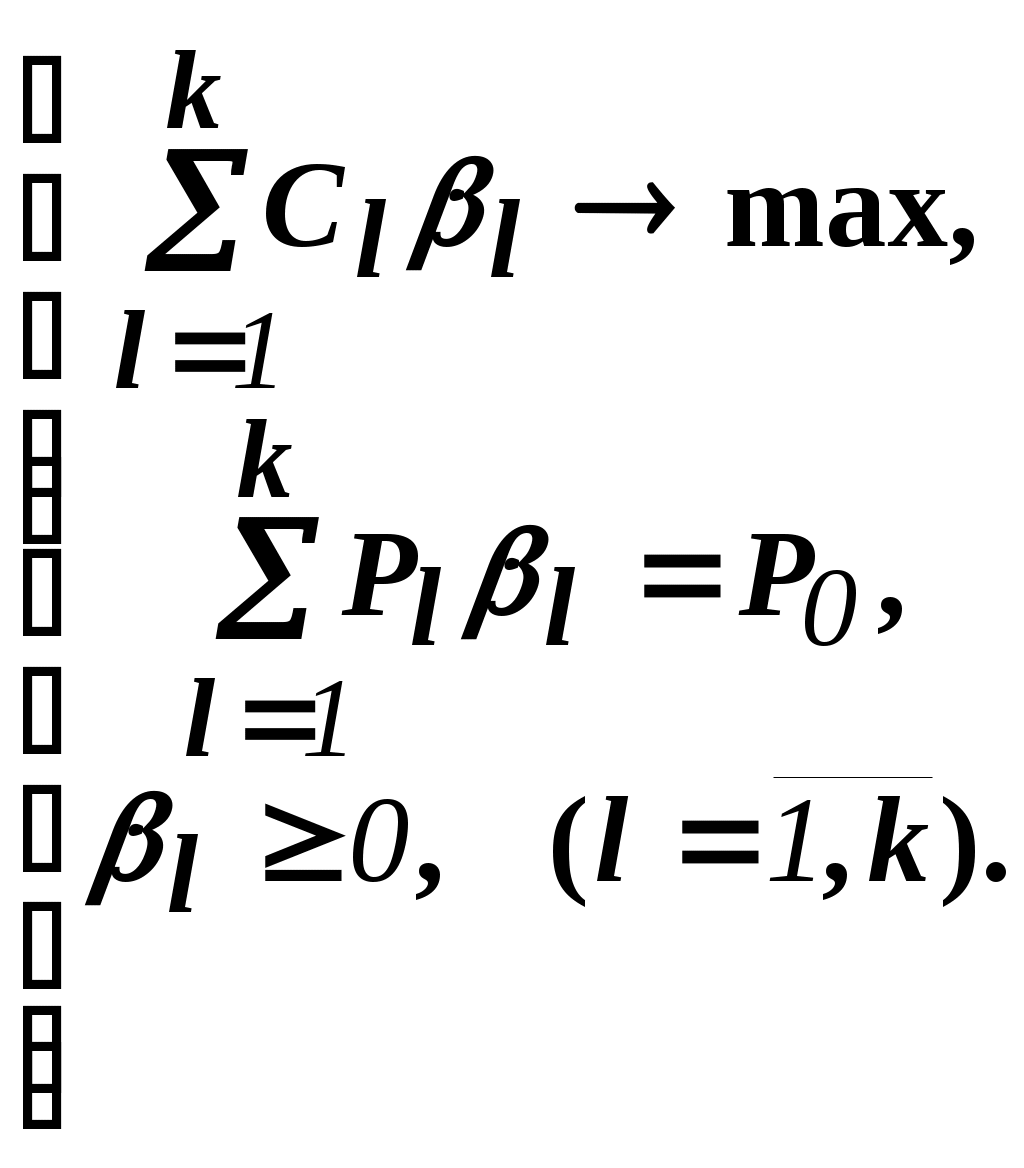 Несмотря на то, что вроде бы уже давно созрел "протест" против такой замены исходной задачи (блочно-диагональной структуры) координирующей задачей, рассмотрим конкретный пример построения координирующей задачи. Пример. 2x1+3x2max, x1+x2 15, -3x1+x2 9, 4x1 +x2 8, x1,2 0. Будем считать, что блок-связка в этой задаче представлен единственным (первым) ограничением. Диагональный блок - вторым и третьим ограничениями. Т.е.: 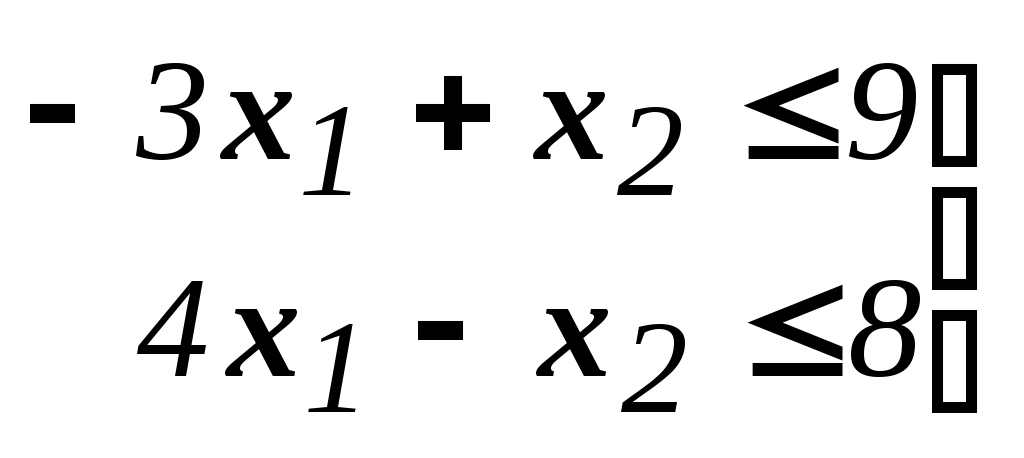 Множество 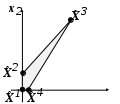 =(2,0) C4=((2,3),(2,0))=4 // =(2,0) C4=((2,3),(2,0))=4 // 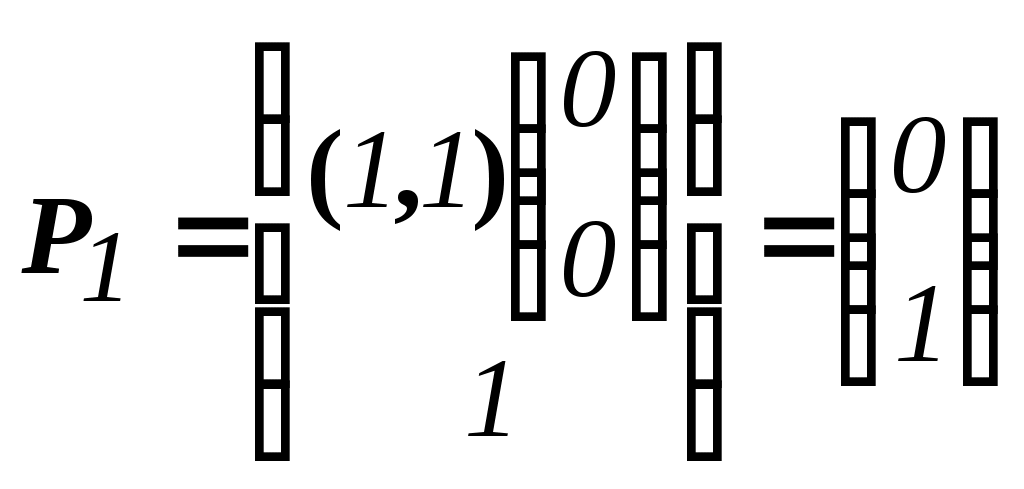 ; ; 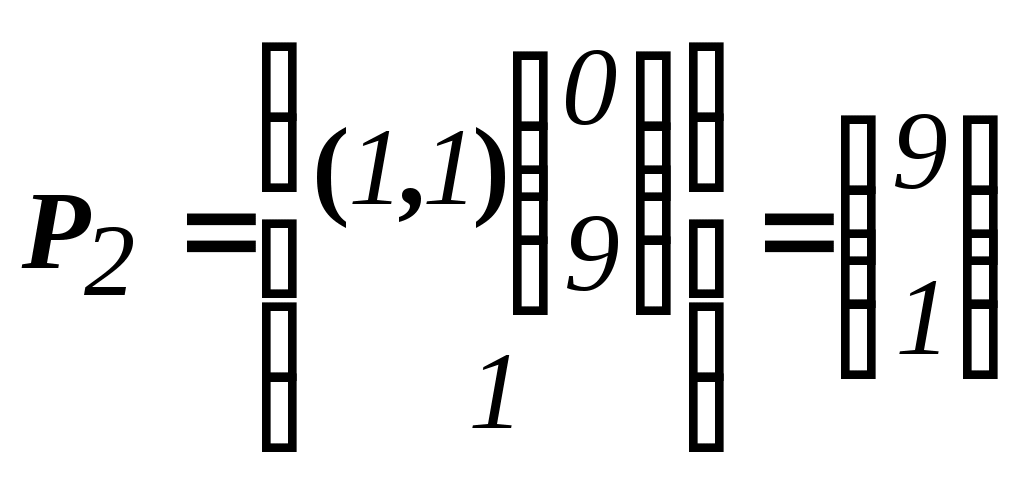 ; ;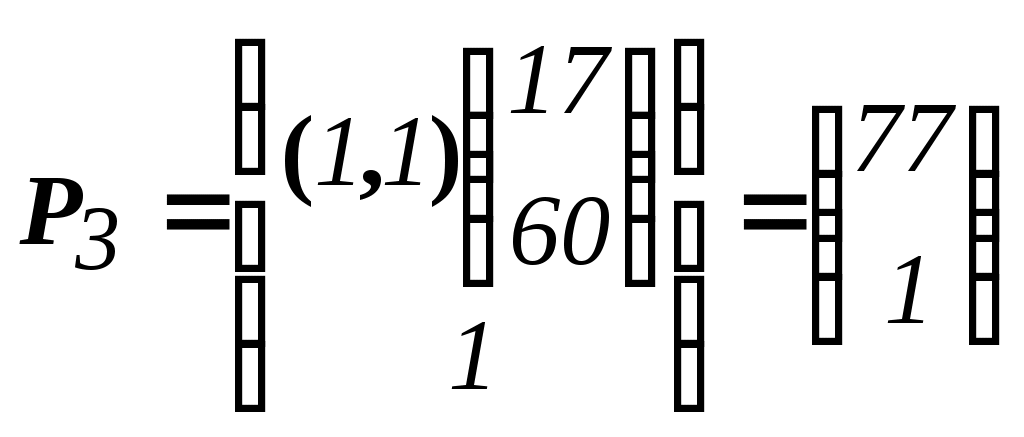 ; ; 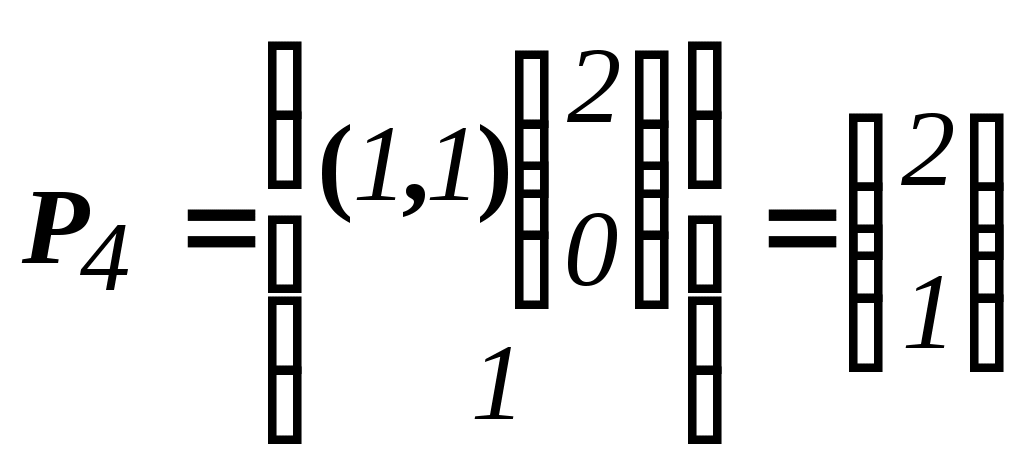 . .Координирующая задача имеет вид: 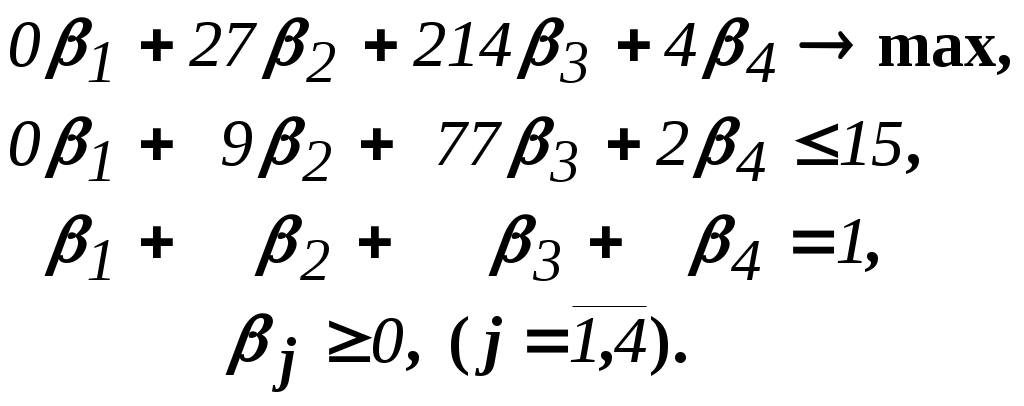 Какие можно сделать выводы? Если сравнить исходную и главную задачи, можно заметить, что исходная задача имеет 3 ограничения и 2 переменные, а главная - 2 ограничения и 4 переменные. В принципе, уменьшение количества ограничений - это хорошо, так как не раз подчеркивалось, что методы ЛП весьма чувствительны к именно к количеству ограничений. Но количество переменных возросло. Нам потребовалось вычислить координаты всех (!) вершин многоугольника, соответствующего диагональному блоку. Мы уже говорили о том, что рассматриваемый метод декомпозиции2 ориентирован на решение задач очень большой размерности. Естественно, что для вычисления координат всех вершин требуется не реализуемая мощность ЭВМ. Короче - это "безнадежное" дело. Так стоит ли игра свеч? Вулф и Данциг - авторы метода декомпозиции - доказали, что решение главной задачи можно искать не зная ни всех вершин многогранника, определенного диагональным блоком, ни (даже!) количества этих вершин. Достаточно знать лишь один (любой) опорный план главной задачи, а также базисную и обратную к ней матрицы соответствующего опорного решения. При этом (что самое важное в методе), координирующая задача в явном виде нигде не записывается3. Остановимся на этом методе подробнее. Идея метода декомпозицииИтак, представим себе главную задачу: 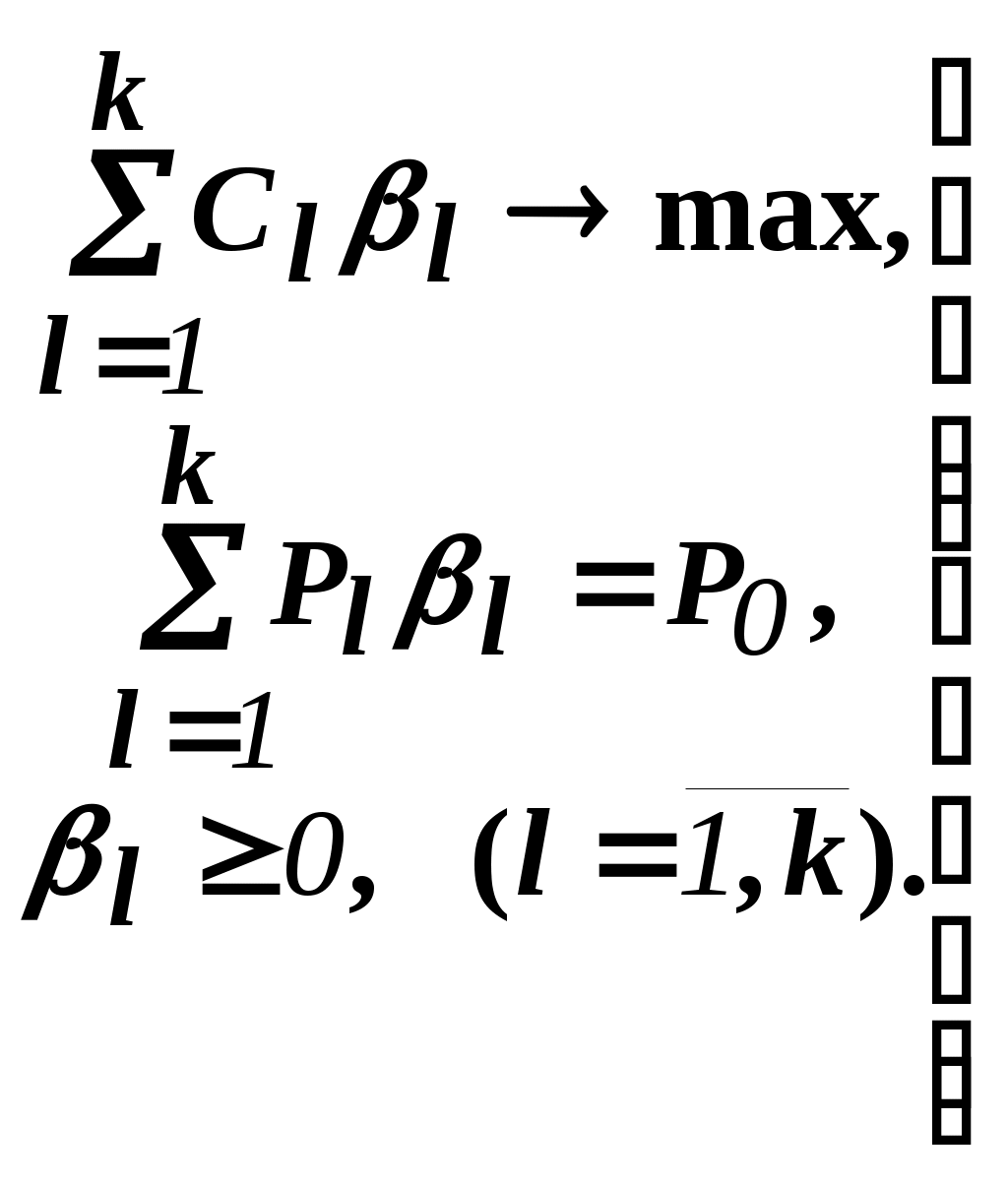 Здесь Здесь 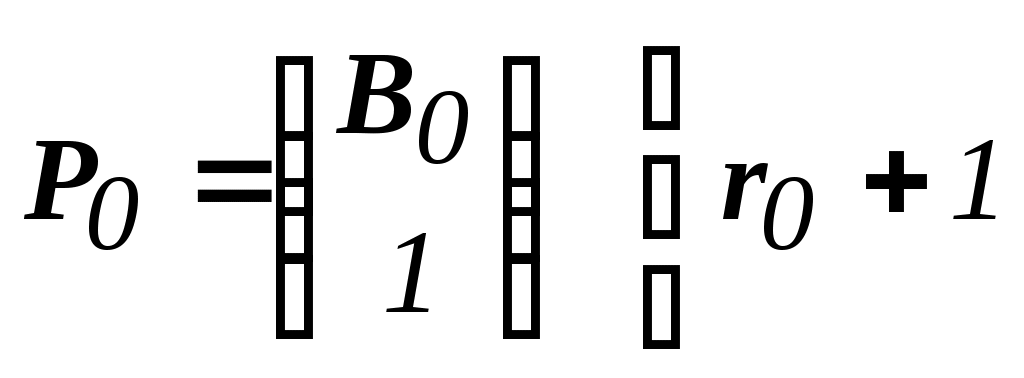 Пусть: B - базисная матрица некоторого опорного решения этой задачи; B-1 - обратная матрица; В соответствии с вычислительной схемой модифицированного симплекс-метода4 (МСМ) текущее решение является оптимальным, если для всех небазисных векторов Начнем анализ этого выражения на предмет исследования возможности его практического использования. Прежде всего "разберемся" с произведением 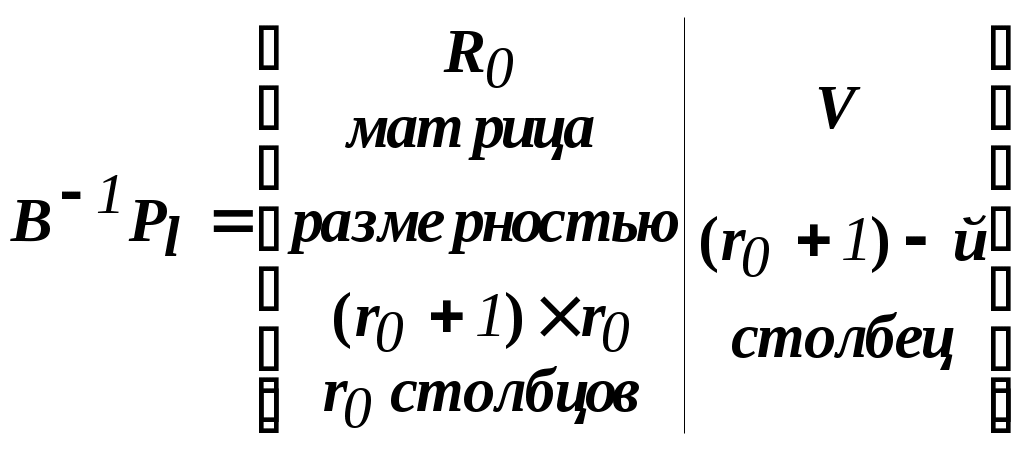 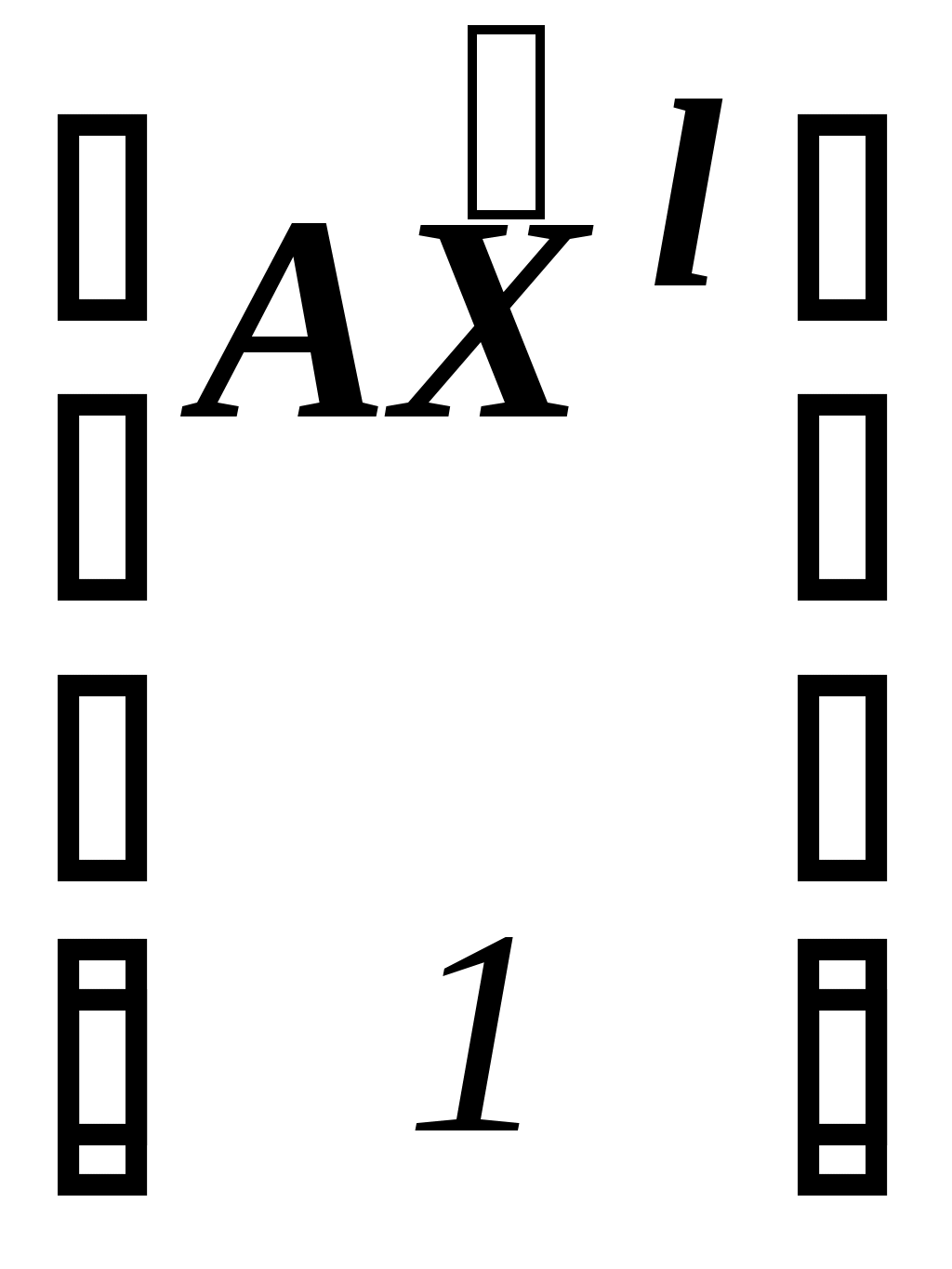 = =Подставим (2) в (1): или (3) Самое интересное начинается здесь! Известно, что если решение не оптимальное, вектор Pl , которому соответствует отрицательная оценка (желательно, максимальная по абсолютной величине), должен быть включен в состав базисных векторов. Проблема же в том, что В свою очередь, численное определение этих элементов невозможно до тех пор, пока не известна соответствующая экстремальная точка То есть, нужно сначала определить эту экстремальную точку. А как ее определить, если мы знаем только обратную матрицу главной задачи B-1 и Сбаз. Сама же задача задана неявно. Ее просто нет! Идея метода Данцига - Вулфа заключается в том, чтобы заменить поиск отрицательной оценки путем последовательного перебора свободных векторов текущего опорного решения направленным поиском только одной экстремальной точки, которой соответствует минимальная оценка связанного с этой точкой вектора главной задачи. Если окажется, что найденная таким образом минимальная оценка неотрицательна, задача решена. Точнее, решена главная задача, а следовательно - и исходная. В противном случае ясно, какой вектор следует вводить в базис: этот вектор будет полностью определен координатами найденной экстремальной точки. Итак, нужно найти экстремальную точку, которой соответствует вектор главной задачи, имеющий минимальную оценку. Это можно сделать, решив следующую задачу: 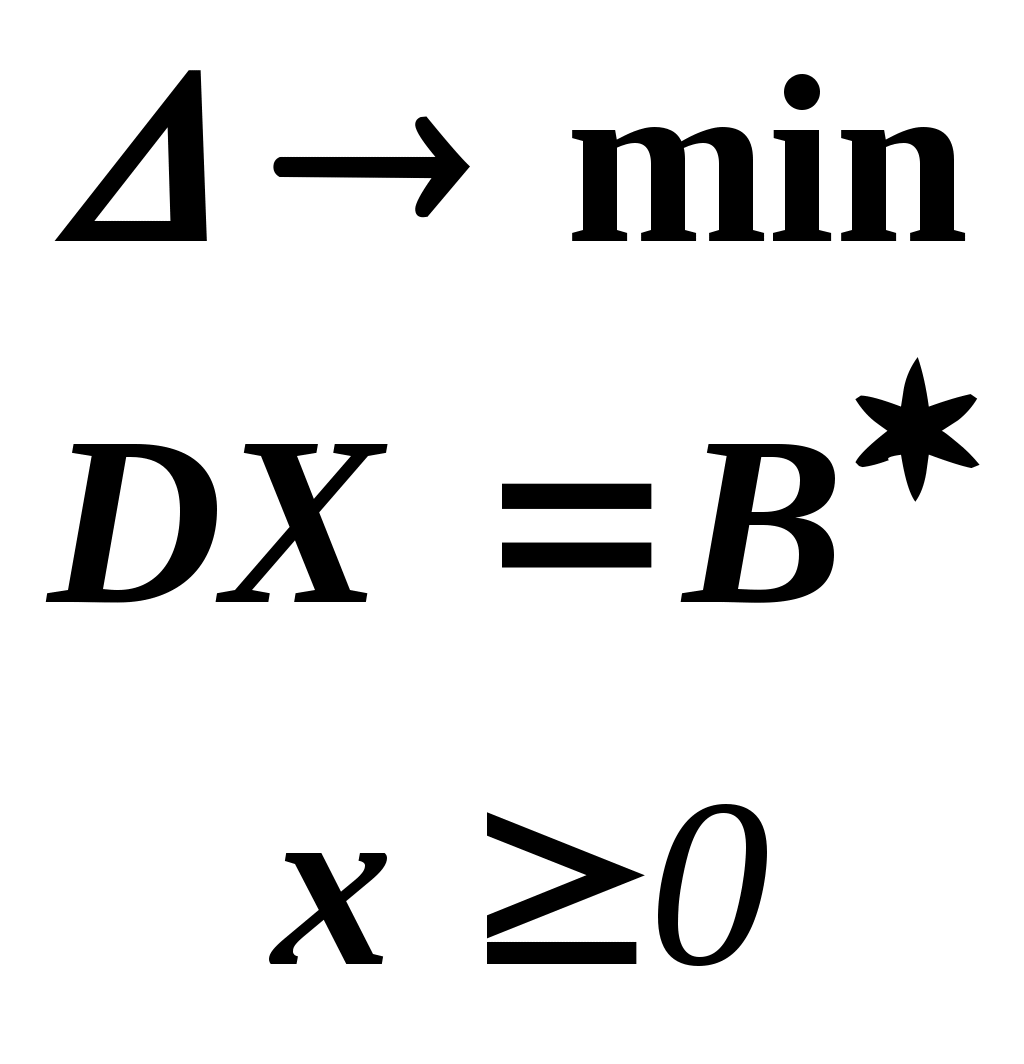 Здесь следует обратить внимание на то, что индекс номера вершины отсутствует. Этот индекс просто неизвестен, т.к. соответствующую вершину еще нужно найти. В качестве переменных этой задачи выступают координаты искомой вершины. Мы предположили, что множество, определенное ограничениями Уже было показано, что: Теперь, опустив индекс l, имеем: Ввиду того, что 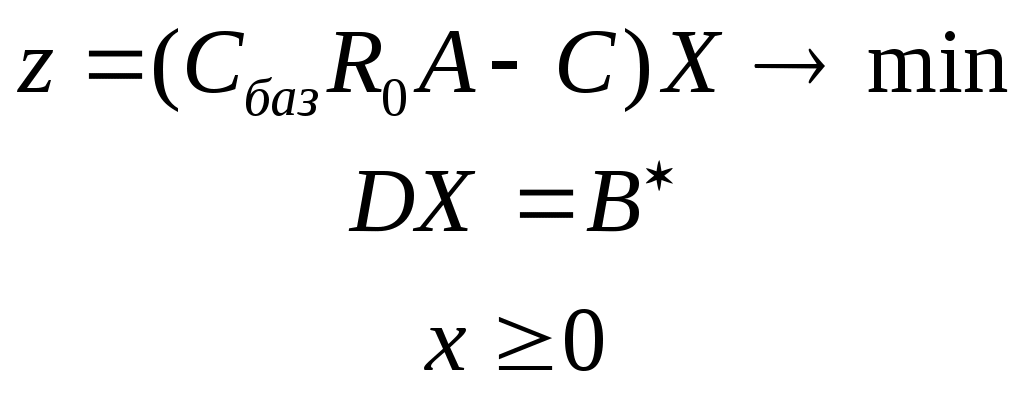 (5) (5)Назовем эту задачу частной (или локальной). Допустим, мы решили эту задачу6 и z* - оптимальное значение ЦФ. Отсюда узнаем и минимальную оценку: и, что самое главное, и сам свободный вектор, который обладает данной оценкой. Действительно, мы знаем координаты экстремальной точки Внимание! Здесь l - это не номер вершины, а номер итерации, на которой данная вершина найдена. Теперь, если Пусть *- множество номеров базисных переменных главной задачи. Тогда, по найденным координатам соответствующих экстремальных точек Если На что здесь следует обратить внимание. Мы используем общие принципы обычного симплекс-метода: последовательно переходим от одного опорного решения координирующей задачи к другому, лучшему. Но при каждом таком переходе мы решаем локальную задачу для поиска вектора с минимальной оценкой. При этом, на каждой итерации формируется "своя" ЦФ локальной задачи7. Декомпозиция в методе Данцига-ВулфаДо сих пор ничего не было сказано о декомпозиции - термине, который фигурирует в названии метода. Более того, мы предположили, что задача имеет один диагональный блок, тем самым, вроде бы "похоронив" саму идею декомпозиции. Это не так. Дело в том, что при решении каждой локальной задачи: 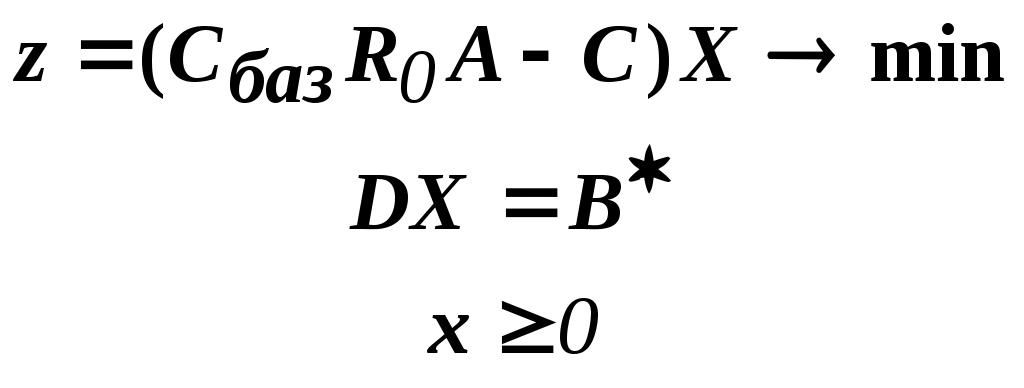 мы сталкиваемся с "чисто" диагональной структурой ее матрицы ограничений (без блока-связки)8. Дело в том, что ............................................................................................ ............................................................................................ Такая структура допускает простое "разрезание" задачи на Lподзадач меньшей размерности. "Сборка" же решения осуществляется следующим образом. Пусть Тогда оптимальное решение локальной задачи определяется: Алгоритм метода декомпозицииДана задача ЛП, ограничения которой составляют блок-связку и ряд диагональных блоков. При решении координирующей задачи будем считать, что имеем один диагональный блок. При решении же частных задач этот блок будет "распадаться" на соответствующие диагональные блоки. Т.е. задача имеет вид: 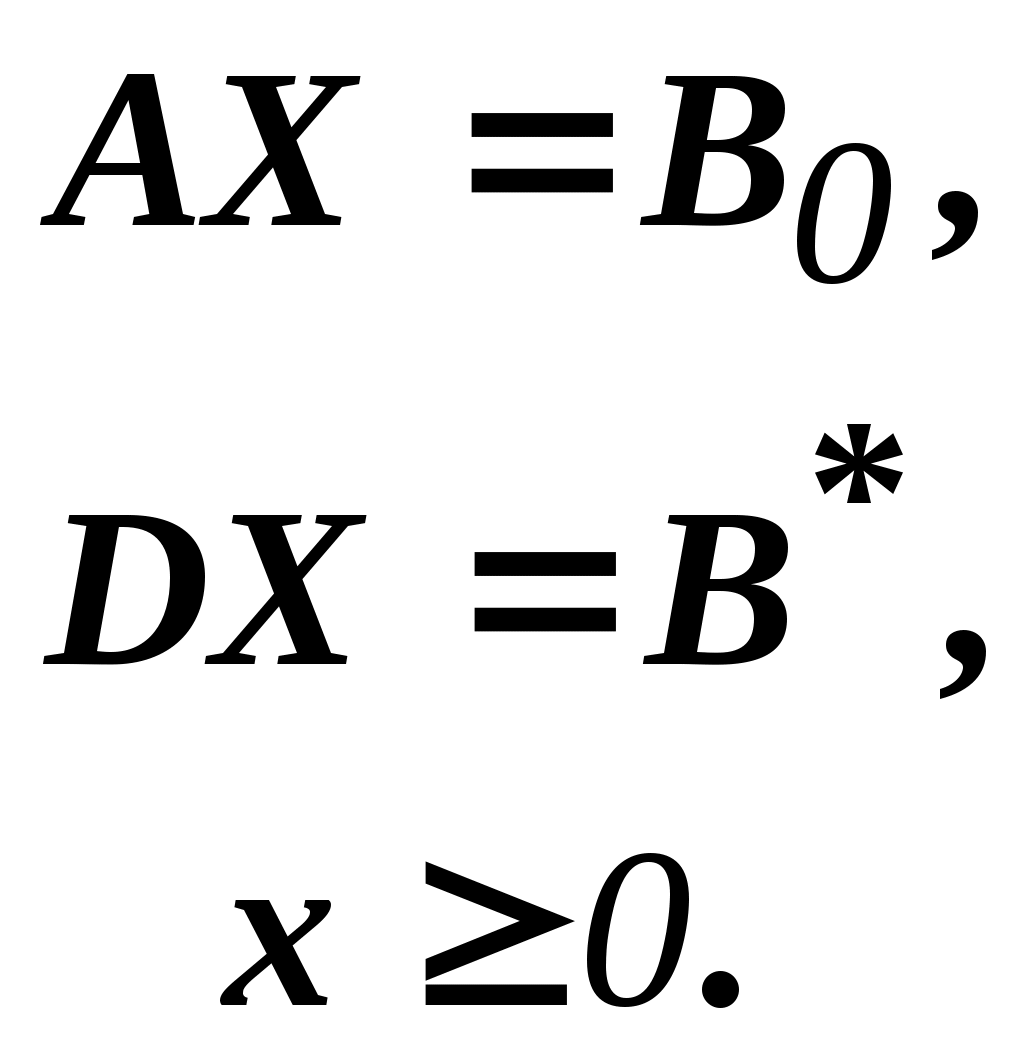 - сохраняем предположение, что допустимое множество задачи не пусто и ЦФ на нем ограничена сверху. Шаг 1. "Построить" координирующую задачу. Конечно же, - условно: мы не в состоянии этого сделать. Однако, структуру этой задачи мы можем представить следующим образом: (1) 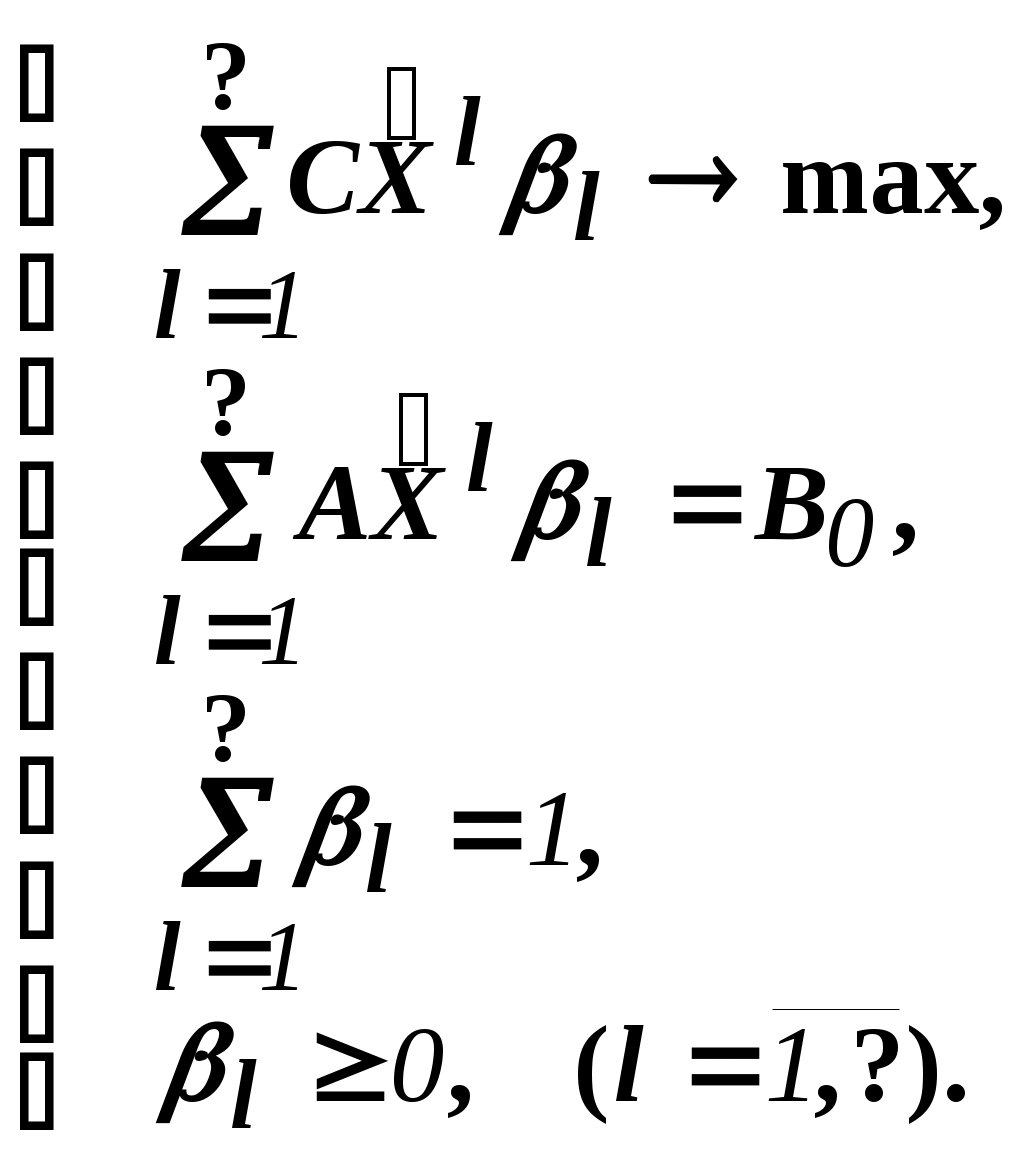 Замечание. Условность этой записи связана еще с одним обстоятельством. Дело в том, что в исходной формулировке ограничения задачи могут быть представлены и уравнениями-ограничениями и нестрогими неравенствами любого направления. Работа же по методу декомпозиции начинается с известного опорного решения координирующей задачи, имеющего, как правило, единичный базис. Для того, чтобы получить такое решение, при сведении координирующей задачи к каноническому виду (с полным набором единичных векторов) в нее вводятся дополнительные и/или искусственные переменные. Это привносит некоторую специфику при реализации метода декомпозиции. При этом координирующую задачу схематически можно представить так:  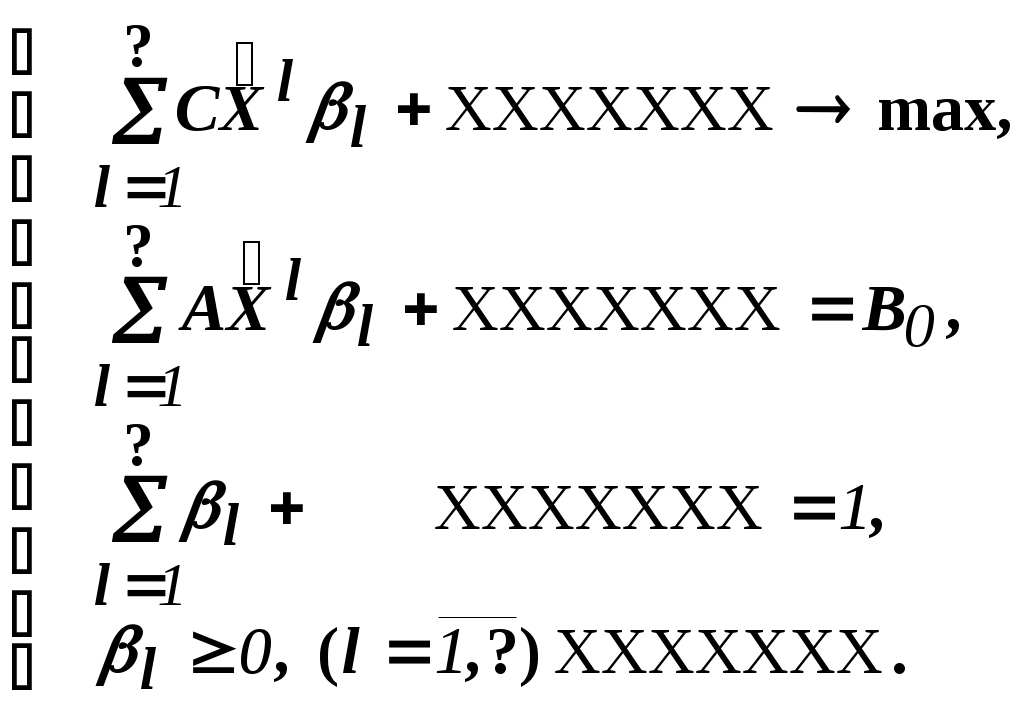 "Область" системы ограничений, по которой строится исходное опорное решение. Переменные Шаг 2. Найти исходное опорное решение координирующей задачи. Обычно для этого используется метод М-задачи: в выделенной области ограничений соответствующие векторы составляют полный единичный базис. Самое интересное, что теперь методом декомпозиции будет решаться координирующая задача, имеющая вид М-задачи! То есть, исходное опорное решение, а также некоторые промежуточные решения будут содержать искусственные переменные в составе базисных. Замечание. Для каждого опорного решения координирующей задачи необходимо будет запоминать не только значения базисных переменных, но и координаты вершин, связанных с основными переменными , если эти переменные входят в состав базисных. Проблема в том, что номеров у этих номеров переменных просто нет и быть не может. Поэтому при обозначении этих переменных будем указывать номер итерации, на которой соответствующая переменная вошла в базис. Чисто технически, мы будем использовать следующий прием. Допустим имеется базис некоторого опорного решения: r0+1 - количество ограничений-уравнений в координирующей задаче. Как уже отмечалось, среди базисных векторов могут быть как основные, так и вспомогательные. Опорному решению поставим в соответствие массив из r0+1 элементов: 
Здесь 0=(0,0,...,0)- n-мерный вектор. Итак, имеем: опорное решение, B - базисная матрица опорного решения; B-1 - обратная матрица; Вычисляем X(P0)=B-1P0 и элементы массива Полагаем l=1 (номер первой итерации). шаг 3 Формируем частную задачу: 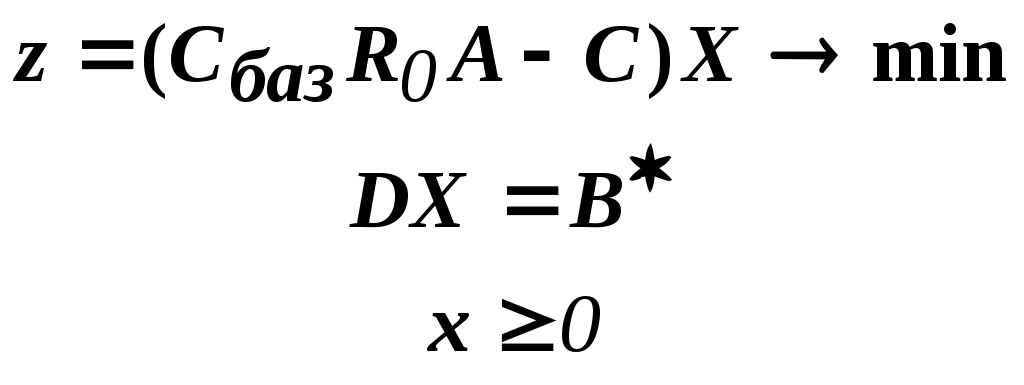 Решаем эту задачу (если D имеет блочно-диагональную структуру, эта задача "распадается" на подзадачи). Собираем решение. z* - оптимальное значение ЦФ; Вычисляем оценку: Если шаг 4. Находим вектор Pl , которому соответствует найденная отрицательная оценка: шаг 5. Ищем разложение этого вектора: X(Pl)=B-1Pl . По обычному для симплекс-метода правилу находим вектор, который нужно вывести из базиса: Корректируем вектор Корректируем массив Формируем новую обратную матрицу 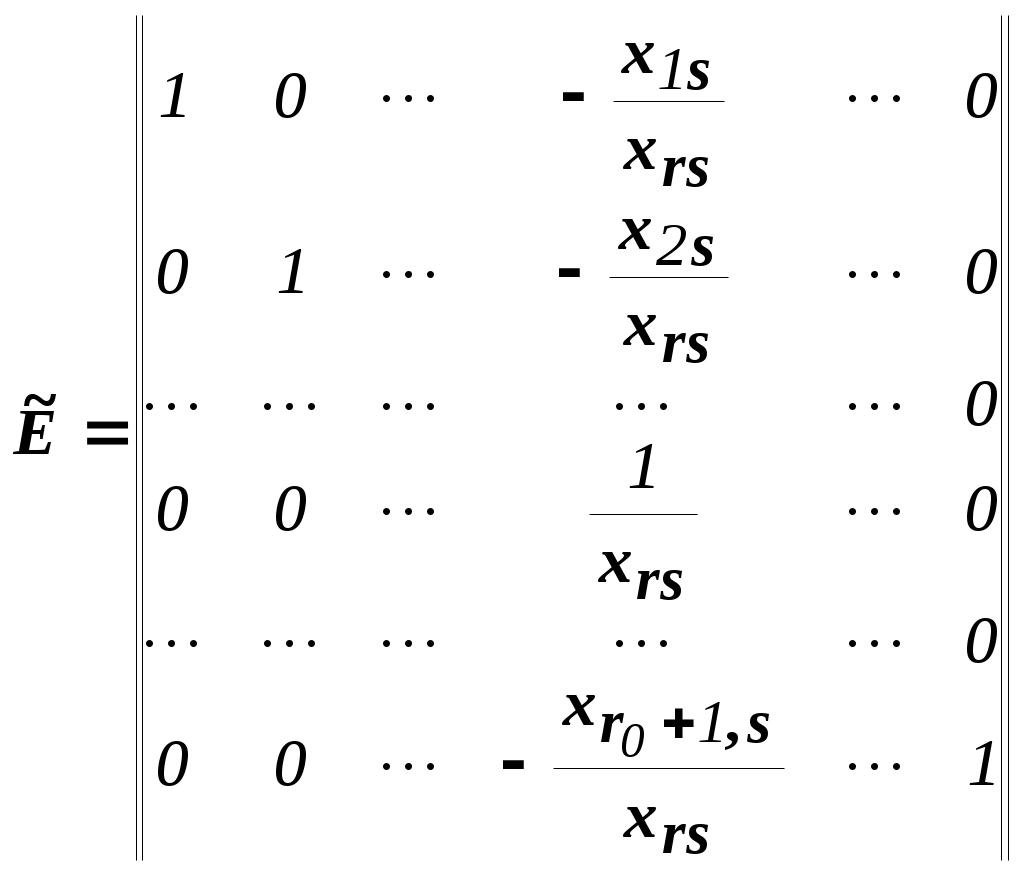 - "почти единичная матрица - "почти единичная матрицаНаходим новое разложение вектора P0 по базису: X(P0)= Положив l=l+1, переходим к шагу 3. шаг 6. Все оценки у основных векторов неотрицательны. Необходимо проверить оценки вспомогательных векторов. Вычисление этих оценок проводим по обычным правилам: Если обнаруживается вспомогательный вектор с отрицательной оценкой (As) , переходим к шагу 5. При этом, в качестве Pl принимаем As . В противном случае выполняем следующий шаг. Шаг 7. Получено оптимальное решение координирующей задачи: Известен массив Восстанавливается решение исходной задачи: 1 В этой связи следует отметить, что важнейшая составляющая процесса решения произвольной задачи нелинейного программирования - это анализ задачи на предмет определения возможности использования той или иной группы методов (например, выпуклый анализ) 2 Непосредственно о декомпозиции речь пока не идет. 3 Достаточно представить (мысленно), что эта задача ЕСТЬ(есть не в памяти ЭВМ, а вообще есть!). 4 Почему МСМ? Дело в том, что именно в рамках схемы МСМ можно не знать коэффициентов разложения тех векторов, чьи оценки нужно вычислить. 5 6 Другого, в предположении, что допустимое множество ограничено, не может быть. 7 Коэффициенты ЦФ локальной задачи определяются через обратную матрицу очередного опорного решения главной задачи. 8 Вспомним задачу, помеченную большим восклицательным знаком. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
