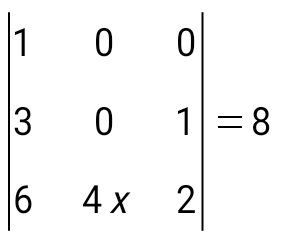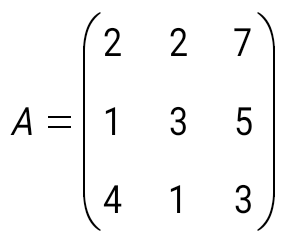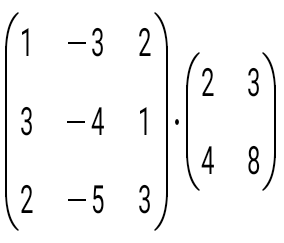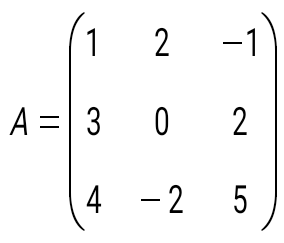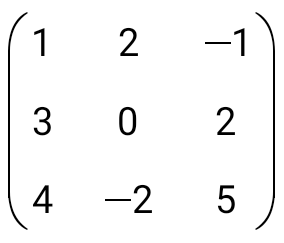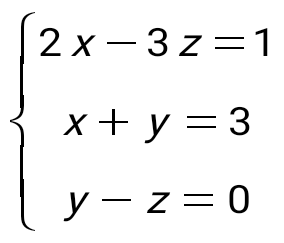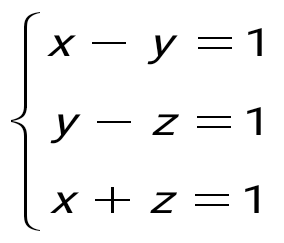матрицасын матрицасын 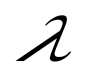 санына көбейту: санына көбейту:
 матрицасының әрбір элементін матрицасының әрбір элементін 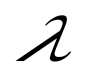 санына көбейтумен мәндес санына көбейтумен мәндес
 және және 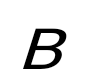 матрицаларын қай кезде көбейтуге болады. матрицаларын қай кезде көбейтуге болады.
бірінші матрицаның баған саны екінші матрицаның жол санына тең болса
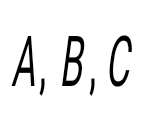 үш матрицаны көбейту үшін қай теңдік орынды: үш матрицаны көбейту үшін қай теңдік орынды:
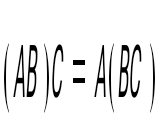 , ,
question> Қай шарт орындалса, матрицалар алмастырылымды деп аталады:
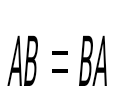
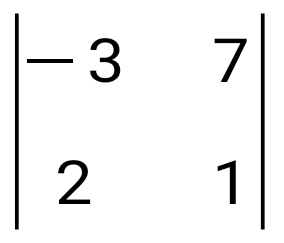 анықтауышын есепте анықтауышын есепте
-17
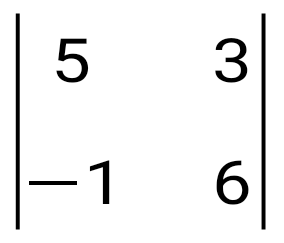 анықтауышын есепте анықтауышын есепте
33
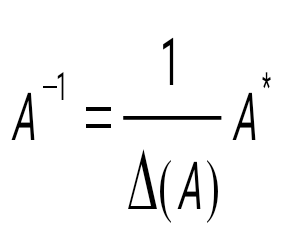
Қандай матрицаның кері матрицасы болады?
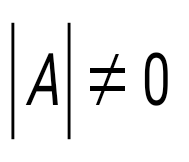 болса болса
 анықтауышының анықтауышының 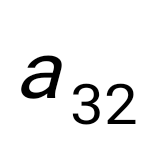 элементінің элементінің  алгебралық толықтауышын есептеңіз: алгебралық толықтауышын есептеңіз:
Теңдеуді шешіңіз 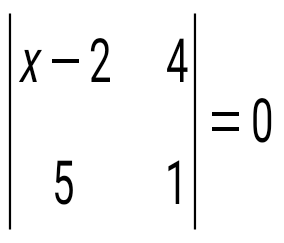
22
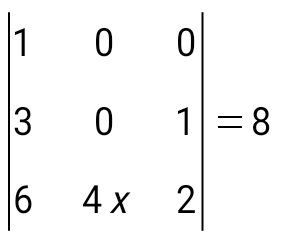 Теңдеуді шешіңіз Теңдеуді шешіңіз
Теңдеуді шешіңіз 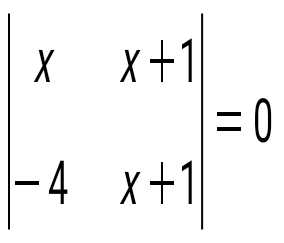
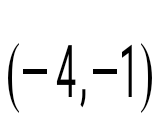
Теңдеуді шешіңіз 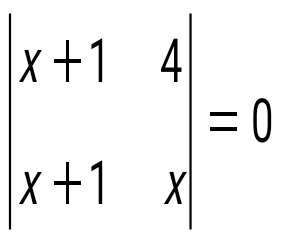
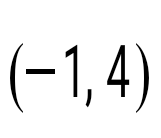
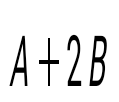 матрицасын есептеңіз, мұндағы матрицасын есептеңіз, мұндағы 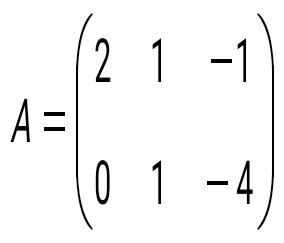 , , 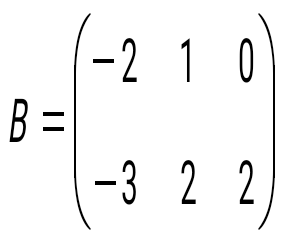
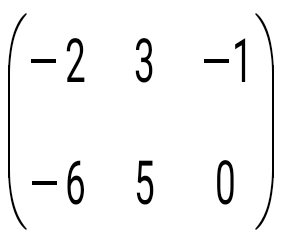
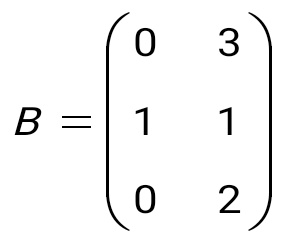  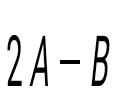 матрицасын табыңыз, мұндағы матрицасын табыңыз, мұндағы 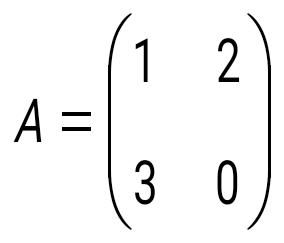 , ,
табу мүмкін емес
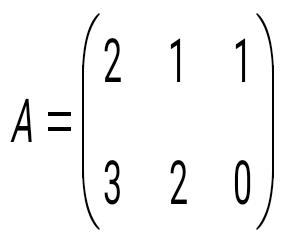 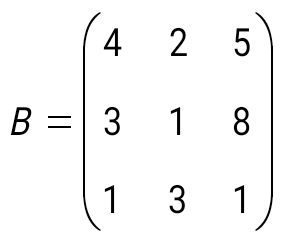 , және матрицаларының қосындысын табыңыз: , және матрицаларының қосындысын табыңыз:
қосу мүмкін емес
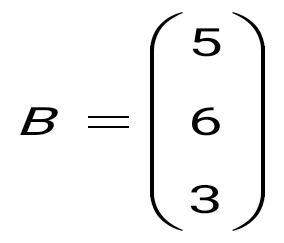 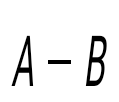 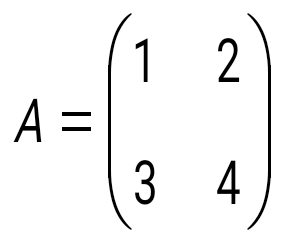 және матрицаларының айырымын табыңыз: және матрицаларының айырымын табыңыз:
азайту мүмкін емес
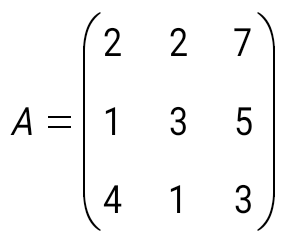 матрицасын 2-ге көбейтіңіз: матрицасын 2-ге көбейтіңіз:
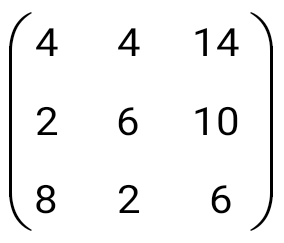
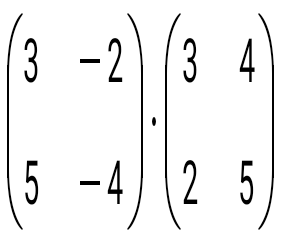 көбейтіндісін есептеңіз: көбейтіндісін есептеңіз:
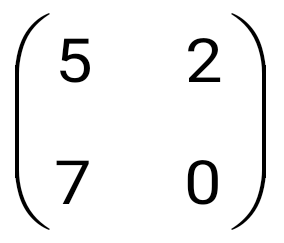
question> 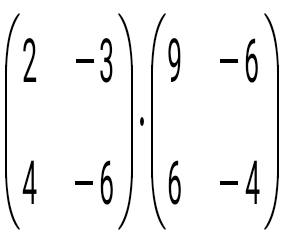 көбейтіндісін есептеңіз: көбейтіндісін есептеңіз:
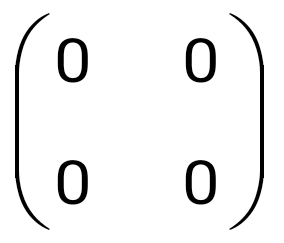
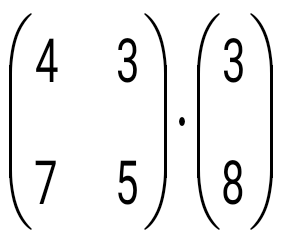 көбейтіндісін есептеңіз: көбейтіндісін есептеңіз:
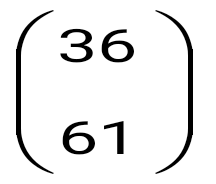
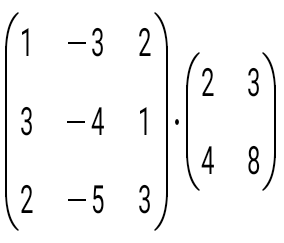 көбейтіндісін есептеңіз: көбейтіндісін есептеңіз:
көбейту мүмкін емес,
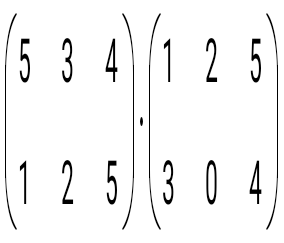 көбейтіндісін есептеңіз: көбейтіндісін есептеңіз:
көбейту мүмкін емес
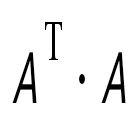 көбейтіндісін есептеңіз, мұндағы көбейтіндісін есептеңіз, мұндағы 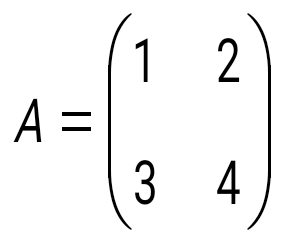 , , 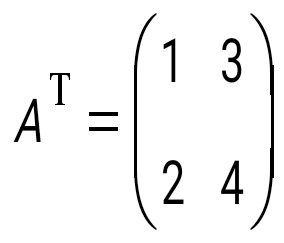 : :
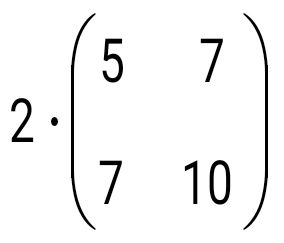
 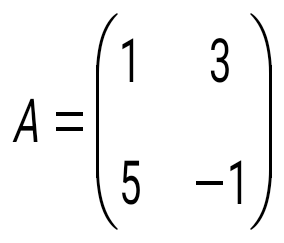
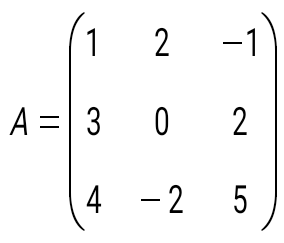 матрицасын бірлік матрицаға көбейтіңіз: матрицасын бірлік матрицаға көбейтіңіз:
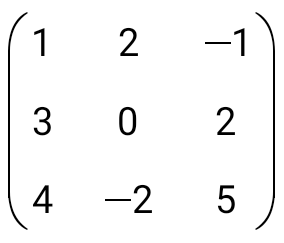
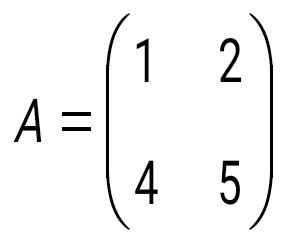 матрицасына кері матрицаны табыңыз: матрицасына кері матрицаны табыңыз:
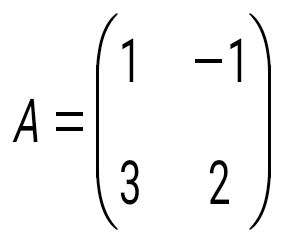 матрицасына кері матрицаны табыңыз: матрицасына кері матрицаны табыңыз:
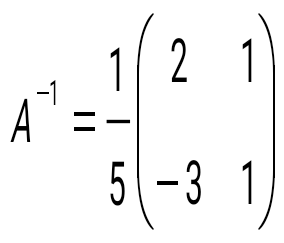
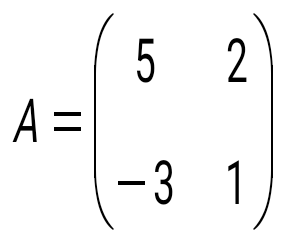 матрицасына кері матрицаны табыңыз: матрицасына кері матрицаны табыңыз:
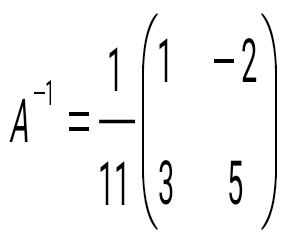
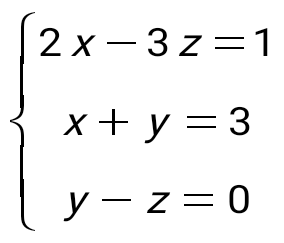 теңдеулер жүйесін шешіңіз: теңдеулер жүйесін шешіңіз:
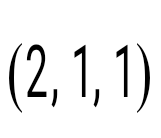
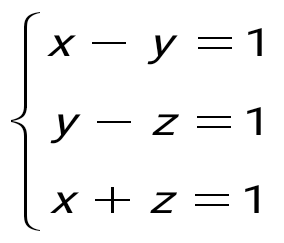 теңдеулер жүйесін шешіңіз: теңдеулер жүйесін шешіңіз:
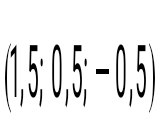
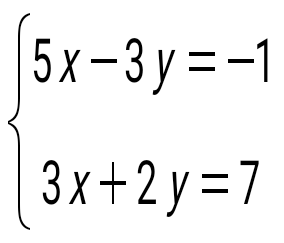 теңдеулер жүйесін шешіңіз: теңдеулер жүйесін шешіңіз:
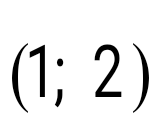
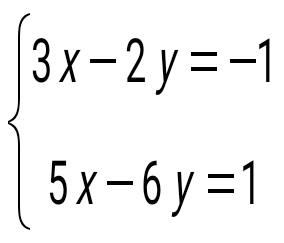 теңдеулер жүйесін шешіңіз: теңдеулер жүйесін шешіңіз:
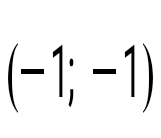
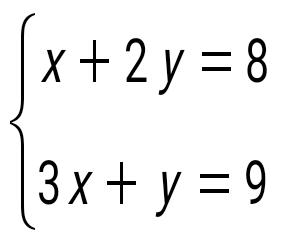 теңдеулер жүйесін шешіңіз: теңдеулер жүйесін шешіңіз:
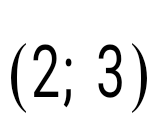
 (3;-2;6) және (3;-2;6) және 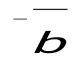 (-2;1 ;0) векторлары берілген. 2 (-2;1 ;0) векторлары берілген. 2 + З + З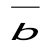 векторының координаттарын тап. векторының координаттарын тап.
(0;-l;12).
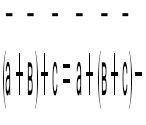 бұл векторлардың қасиеті: бұл векторлардың қасиеті:
ассоциативтілік.
Екі векторр тең деп аталады, егер:
векторлардың модульдері тең, коллинеар және бірдей бағытталған болса.
  (4;3;3) және (4;3;3) және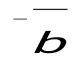 (3;2;4) векторлары берілген. және (3;2;4) векторлары берілген. және 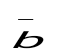 векторларының скаляр көбейтіндісін тап. векторларының скаляр көбейтіндісін тап.
30.
Егер 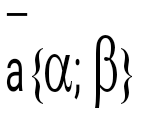 болса, онда бұл вектордың болса, онда бұл вектордың 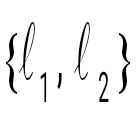 базисіндегі жіктелуі: базисіндегі жіктелуі:
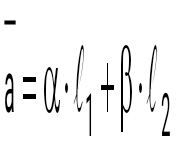 . .
question>  және және  векторларының арасындағы бұрыштың косинусын есептейтін формула: векторларының арасындағы бұрыштың косинусын есептейтін формула:
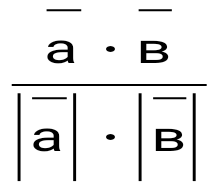 . .
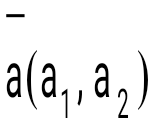 және және 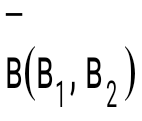 векторларының скаляр көбейтіндісі дегеніміз: векторларының скаляр көбейтіндісі дегеніміз:
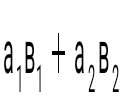 . .
Егер 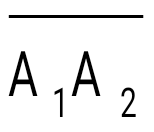 векторы А1(х1, у1, z1) басының координаттарымен және А2 (х2, у2, z2) ұшының координаттарымен берілсе, онда вектордың координаттары тең: векторы А1(х1, у1, z1) басының координаттарымен және А2 (х2, у2, z2) ұшының координаттарымен берілсе, онда вектордың координаттары тең:
ұшы мен басының сәйкес координаттарының айырмасына.
question> Егер 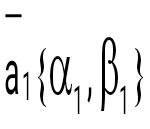 және және 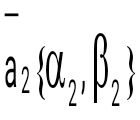 векторлары үшін векторлары үшін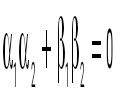 шарты орындалса, онда бұл векторлар: шарты орындалса, онда бұл векторлар:
перпендикуляр.
 (-2;6;-3) және (-2;6;-3) және |
 Скачать 1.82 Mb.
Скачать 1.82 Mb.