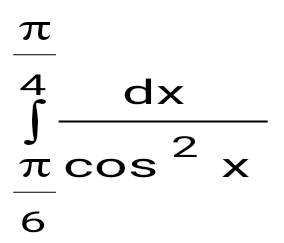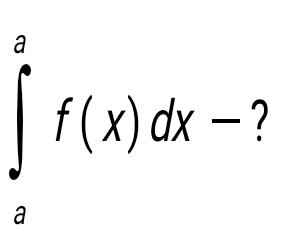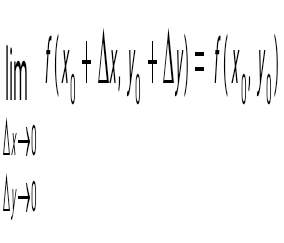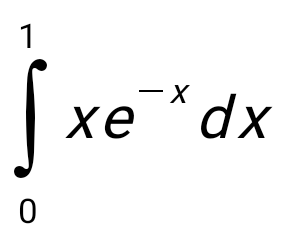 : :
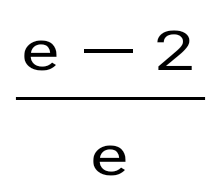 . .
Анықталмаған интегралды тап: 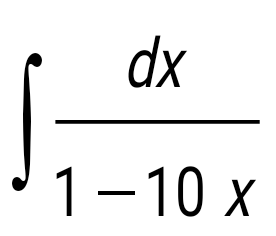 . .
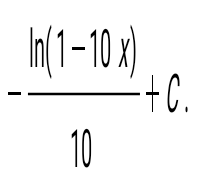
х = 5, у = 0, у =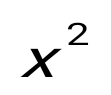 сызықтарымен шектелген фигураның ауданын тап: сызықтарымен шектелген фигураның ауданын тап:
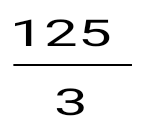 . .
question> х = 0, х = , у = 0, у = sinx сызықтарымен шектелген фигураның ауданын тап:
2.
х = 2, у = 0, у = 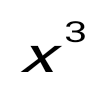 сызықтарымен шектелген фигураның ауданын тап: сызықтарымен шектелген фигураның ауданын тап:
4.
Есепте: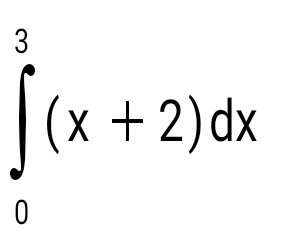 : :
10,5.
Интегралды тап: 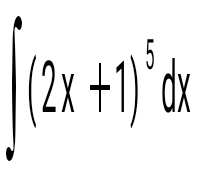 : :
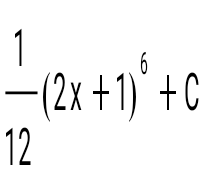 . .
question> Есепте: 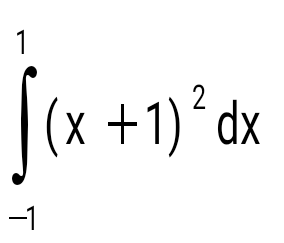 : :
8/3.
у = 0, у = 3х – 3, х = 2 сызықтарымен шектелген фигураның ауданын тап:
3/2.
у = 0, у = х, х = 4 сызықтарымен шектелген фигураның ауданын тап:
8.
Анықталмаған интегралды тап: 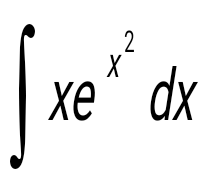 . .
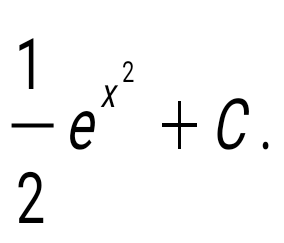
question> анықталған интегралдың мәні:
4
Есепте 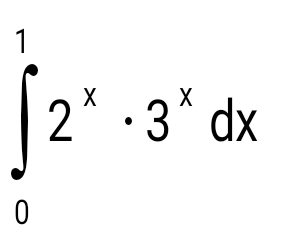 : :
5/ ln 6.
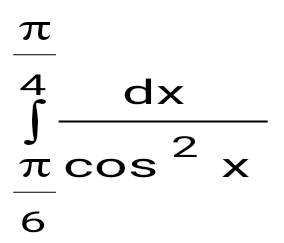 Есепте: : Есепте: :
1 -.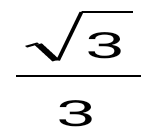
Есепте: 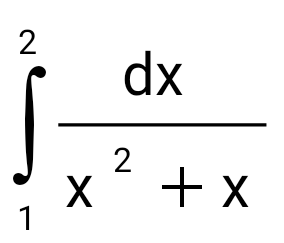 : :
ln 4/3.
Есепте: 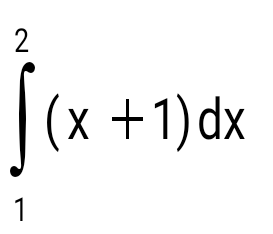 : :
5/2.
Ньютона-Лейбниц формуласы:
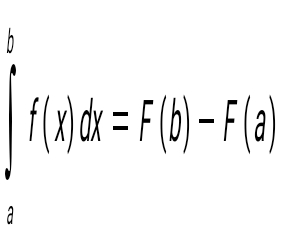 . .
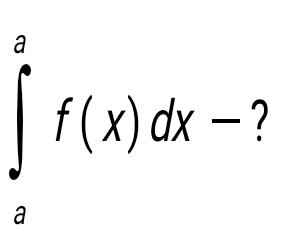 : :
0.
Анықталған интегралдың келесі қасиетін жалғастырып аяқта. Интегралдау шектерінің орнын ауыстырғанда:
интегралдың таңбасы өзгереді.
Денені Ох өсін айналдыра бұрғаннан пайда болған дененің көлемі қандай формула арқылы өрнектеледі?:
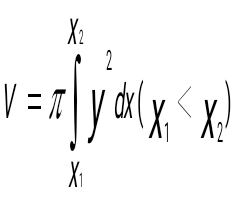 . .
Денені Оу өсін айналдыра бұрғаннан пайда болған дененің көлемі қандай формула арқылы өрнектеледі ?:
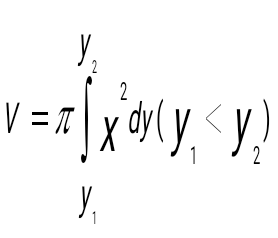 . .
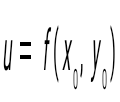 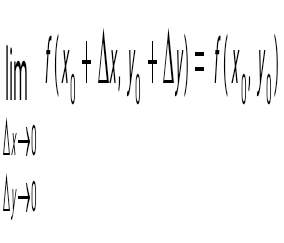 Сөйлемді аяқта: егер болса, онда функциясы Сөйлемді аяқта: егер болса, онда функциясы 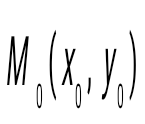 нүктесінде … болады: нүктесінде … болады:
дифференциалданатын.
Егер u=f(x,y) функциясының жоғарғы ретті үзіліссіз аралас туындылары бар болса, онда келесі қатынас орындалады:
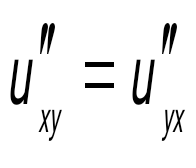 . .
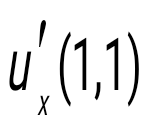 Егер Егер 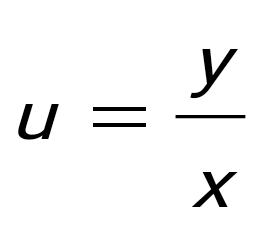 болса, - ті есепте: болса, - ті есепте:
–1
Егер Z=ylnx болса, 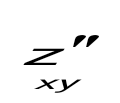 -ті есепте: -ті есепте:
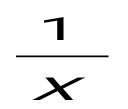
z=f(х,у) функцияның х бойынша дербес туындысы деп аталады:
∆х→0 ұмтылғанда функцияның х бойынша дербес өсімшесінің х аргументтің өсімшесіне қатынасының шегін айтады, бұл жағдайда қалған аргумент өзгеріссіз қалады.
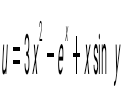 Егер болса, Егер болса, 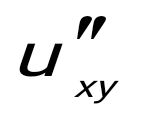 -ті есепте: -ті есепте:
cosy
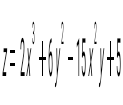 функциясы үшін А(1;-1) нүктесіндегі функциясы үшін А(1;-1) нүктесіндегі 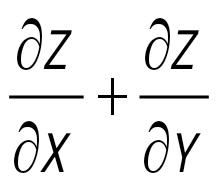 өрнегінің мәнін тап: өрнегінің мәнін тап:
9
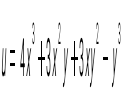 функциясы үшін функциясы үшін 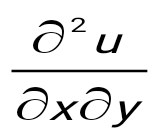 -ті тап: -ті тап:
6(x+y)
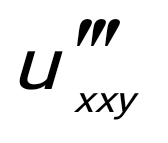 x=y=1 болғанда x=y=1 болғанда 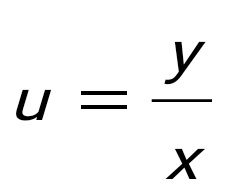 функциясы үшін -ті тап: функциясы үшін -ті тап:
2.
question> 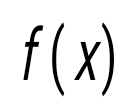 функциясы тақ деп аталады, егер : функциясы тақ деп аталады, егер :
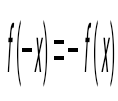 . .
f(x)=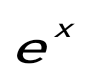 -1 функциясы берілген. f(-1)- ны табыңдар: -1 функциясы берілген. f(-1)- ны табыңдар:
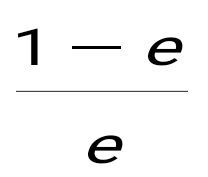 . .
у= 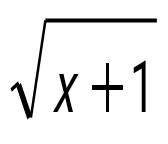 функцияның анықталу облысын табыңдар: функцияның анықталу облысын табыңдар:
х≥-1.
Тақ функцияның графигі неге қарағанда симметриялы болады?:
координата басына
question> у=1/(4-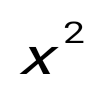 ) функцияның анықталу облысын табыңдар: ) функцияның анықталу облысын табыңдар:
(-∞;-2)U (-2;2) U(2;+∞).
Егер функцияның графигі координаттар басына қарағанда симметриялы болса, онда ол:
тақ.
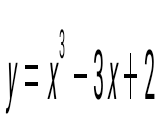 функцияның анықталу облысын табыңдар: функцияның анықталу облысын табыңдар:
(-∞;+∞).
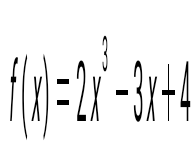 функциясы берілген. f(-2)-ні тап: функциясы берілген. f(-2)-ні тап:
–6.
question> 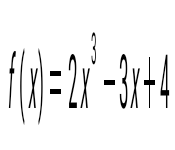 функциясы берілген. f(1)-ді тап: функциясы берілген. f(1)-ді тап:
3.
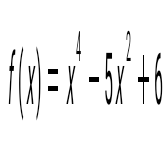 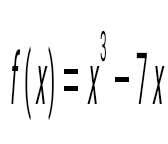 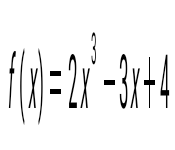 функциясы берілген. f(0)-ді тап: функциясы берілген. f(0)-ді тап:
4.
|
|
|
|
|
|
|
|
|
|
|
Функцияберілді1)
4)f(x)=sinx+ sinx/2;5)f(x)=cos2x sinx/2;5)f(x)=cos2x
|
6)
|
2)
|
3)f(x)=x-
.Жұпфункциялардыкөрсетіңдер:
|
1,5.
|
|
|
|
|
|
|
|
|
|
|
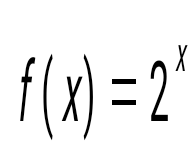 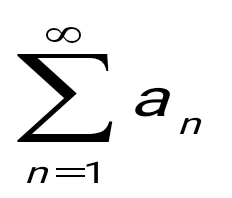 , мүшелірі оң санды қатардың, , мүшелірі оң санды қатардың, 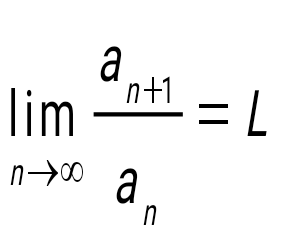 - Даламбер белгісі бойынша жинақталу егер : - Даламбер белгісі бойынша жинақталу егер :
L<1.
question> 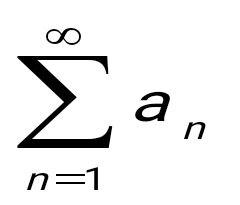 санды қатардың қажеттілік шарты: санды қатардың қажеттілік шарты:
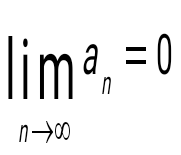 . .
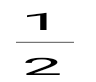   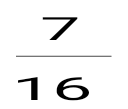 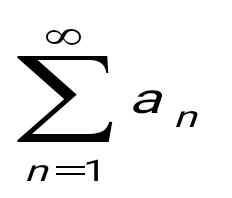 + + + +... қатарын түрінде жаз: + + + +... қатарын түрінде жаз:
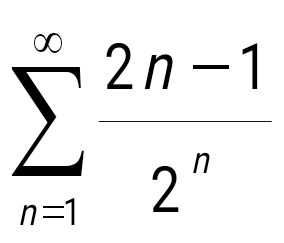
.
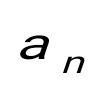 1+ 1+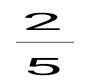 + +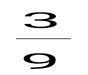 + +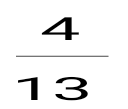 +... қатарын +... қатарын 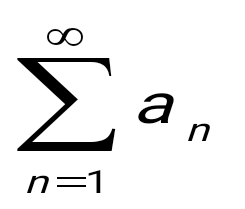 түрінде жаз, мұндағы -қатардың жалпы мүшесі. түрінде жаз, мұндағы -қатардың жалпы мүшесі.
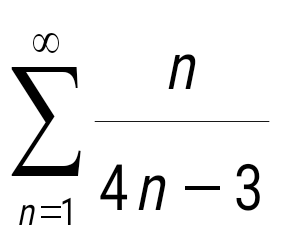 . .
.
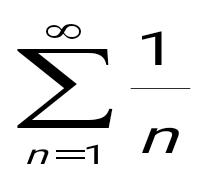 қатары қатары
Гармоникалық.
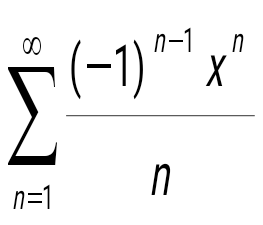 Жинақталу интервалын тап: Жинақталу интервалын тап:
.
(-1;1).
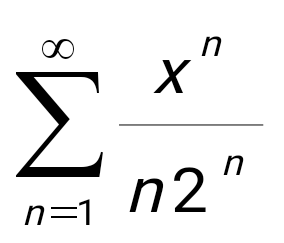 Жинақталу интервалын тап: Жинақталу интервалын тап:
.
(-2;2).
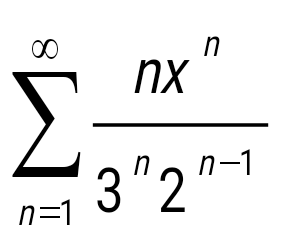 Жинақталу интервалын тап: . Жинақталу интервалын тап: .
(-6;6)
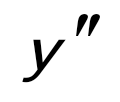 -тап , егер -тап , егер 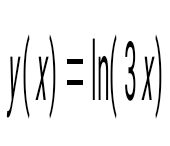 : :
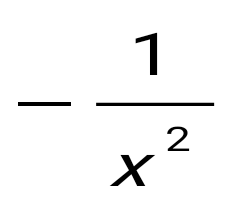
 : :
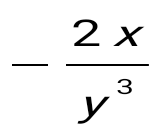 . .
|
 Скачать 1.82 Mb.
Скачать 1.82 Mb.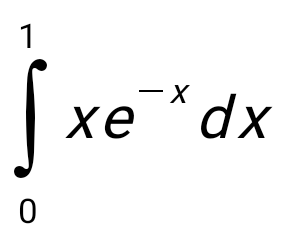 :
: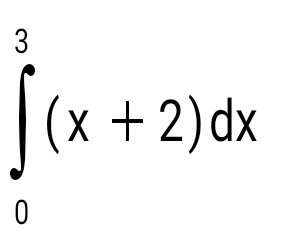 :
: