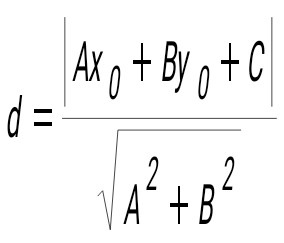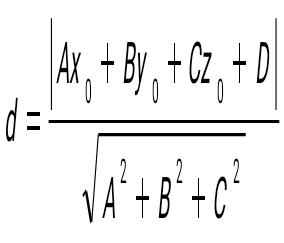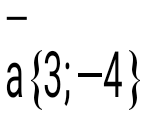 және және 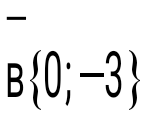 векторлары берілген. Олардың модульдерін тап: векторлары берілген. Олардың модульдерін тап:
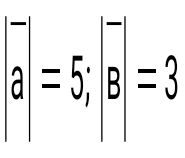 . .
А(1;-2;3), В(0;4;-1) және С(1;2;3) нүктелері берілген. АВ және AC векторларының скаляр көбейтіндісін тап.
24.
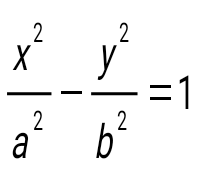 теңдеуі қандай қисықты береді? теңдеуі қандай қисықты береді?
Гипербола
эллипстін канондық теңдеуі
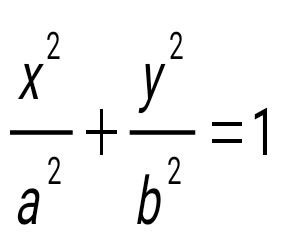
у2=-20х параболасының директриссасының теңдеуін көрсет:
х=-10.
3х-2у-7=0 және х+3у-6=0 түзулерінің қиылысу нүктесін тап.
(3; 1).
А(2; 0), В(4; 2), С(2; 6) нүктелері берілген. А А1 медианасының теңдеуін тап:
4х-у-8=0.
А(4; 3) нүктесінен 3х+4у-10=0 түзуіне дейінгі ара қашықтықты тап:
2,8.
Егер М(-3;-2) и N(l;6) болса, онда А(-2;1) нүктесі арқылы өтетін MN түзуіне параллель болатын түзудің теңдеуін тап.
2х-у+5=0.
question> АВ кесіндісінің ұштары берілген: А(-3; 7), В (5; 11). Кесіндінің ортасын тап:
(1; 9).
Егер А (-2; 0), С (4; 2) болса, онда АС кесіндісінің ұзындығын тап:
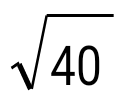 . .
(-3; 4) нүктесінен ОХ осіне дейінгі қашықтықты тап:
4.
Фокустары координаттар басына қатысты симметриялы болып абцисса осі бойында орналасатын гиперболаның теңдеуін құрыңыз, егер оның остері 2а=10, 2в=8:
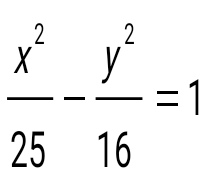 . .
 нүктелерінің ара қашықтығын есептейтін формула: нүктелерінің ара қашықтығын есептейтін формула:
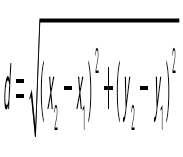 . .
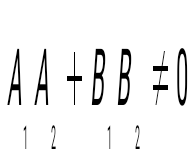 жағдайындағы жағдайындағы 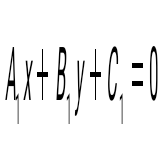 және және 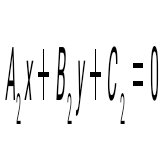 түзулерінің арасындағы бұрыштың тангенсының формуласын жазыңыз: түзулерінің арасындағы бұрыштың тангенсының формуласын жазыңыз:
tg α = 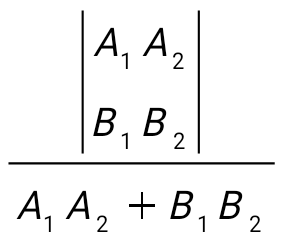 . .
x - 3y = 0 түзуінің k және b параметрлерін анықтаңыз:
k =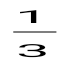 ; b = 0. ; b = 0.
Келесі түзулердің қайсысы координаттар басынан өтеді:
1) х + у = 0; 2) х – у = 0; 3) 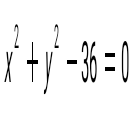 4) 4) 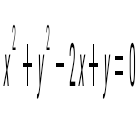 5) 5) 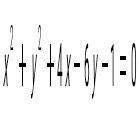
1) және 2).
Төбелері O(0;0), А(8;0) және В(0; 6) болатын үшбұрыштың ОМ медианасының ұзындығын анықта.
5.
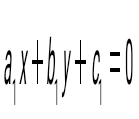 және және 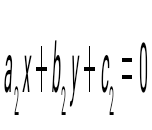 түзулерінің перпендикулярлық шарты: түзулерінің перпендикулярлық шарты:
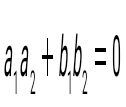
Центрі (0; 0) және радиусы 4 болатын шеңбердің теңдеуін жаз:
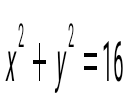
А (4; -1) нүктесіне Оy осіне қатысты симметриялы нүкте қандай?:
(-4; -1).
у = х + 4 түрінде берілген L түзуінің Оx осімен қиылысу бұрышын анықта:
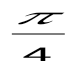 . .
2х – у = 6 түзуін кесінділер теңдеуі түрінде жаз:
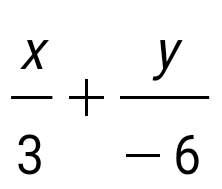 = 1. = 1.
х + у = -4 түзуіне қандай нүкте тиісті болады:
(-2; -2).
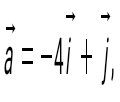 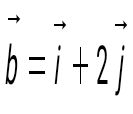 . Есепте . Есепте 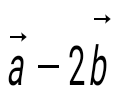 : :
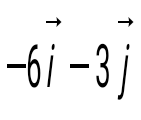 . .
Гиперболаның теңдеуі:
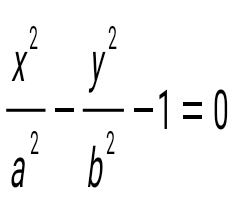 . .
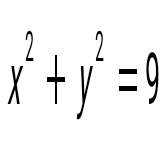 шеңберінің радиусы неге тең?: шеңберінің радиусы неге тең?:
3.
question> Егер А (2; 3; 4), В (5; 6; 8) болса, онда 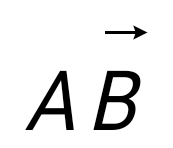 векторының координаттарын тап: векторының координаттарын тап:
(3; 3; 4).
у=3x-4 түзуіне параллель және М(2:1) нүктесі арқылы өтетін түзудің теңдеуін тап:
y=3x-5.
А(2;1;-1) нүктесі арқылы өтетін және нормаль векторы 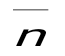 (1;-2;3) болатын жазықтықтың теңдеуін құр. (1;-2;3) болатын жазықтықтың теңдеуін құр.
x-2y+3z+3=0 .
k-ның қандай мәнінде 3x-5y+kz-3=0 және x-3y+2z+5=0 жазықтықтары перпендикуляр болады.
-9.
question> Бұрыштық коэффициенті 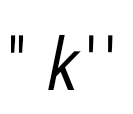 -ға тең, -ға тең, 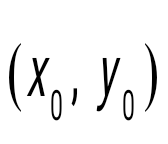 нүктесі арқылы өтетін түзудің теңдеуі келесі түрде жазылады нүктесі арқылы өтетін түзудің теңдеуі келесі түрде жазылады
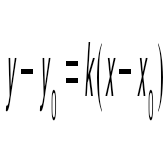
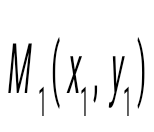 және және 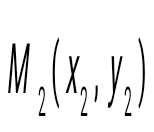 нүктелері арқылы өтетін түзудің теңдеуін көрсет нүктелері арқылы өтетін түзудің теңдеуін көрсет
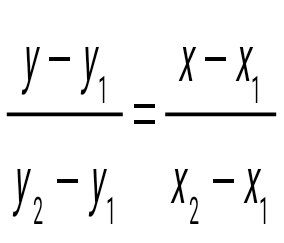
Түзудің жалпы теңдеуін көрсет
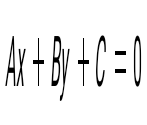
Бұрыштық коэффициентпен берілген түзудің теңдеуін көрсет
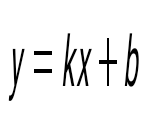
Түзудің кесінділік теңдеуін көрсет
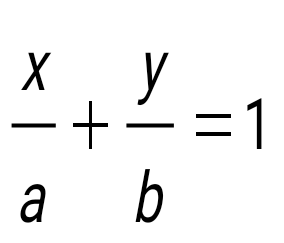
Берілген 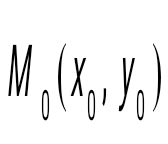 нүктеден берілген нүктеден берілген 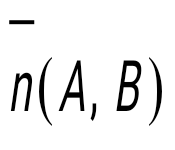 векторға перпендикуляр өтетін түзудің теңдеуін көрсет векторға перпендикуляр өтетін түзудің теңдеуін көрсет
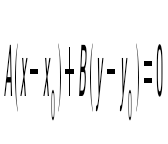
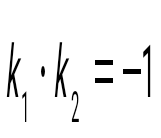 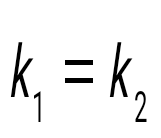 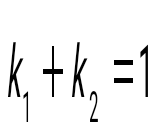 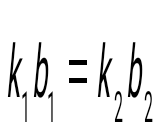 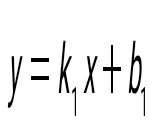 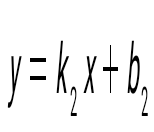 және түзулерінің перпендикулярлық белгісін көрсет және түзулерінің перпендикулярлық белгісін көрсет
Нүктеден түзуге дейінгі қашықтық қайсы формуламен есептелініледі:
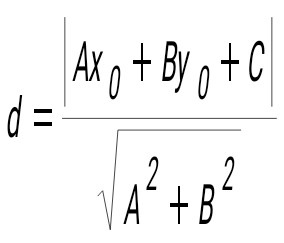
|
және
|
түзулерініңпараллельдікбелгісінкөрсет
|
|
Берілген
|
нүкте арқылы, берілген векторға
|
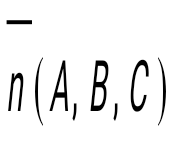 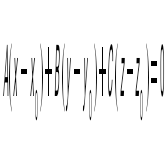 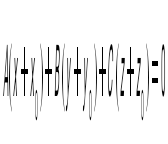 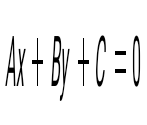 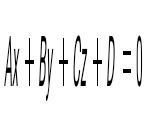 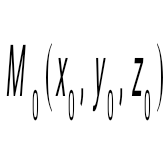    перпендикуляр өтетін жазықтықтың теңдеуін көрсет перпендикуляр өтетін жазықтықтың теңдеуін көрсет
Жазықтықтың жалпы теңдеуін көрсет
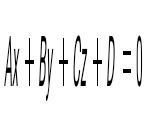
Жазықтықтың кесінділік теңдеуін көрсет
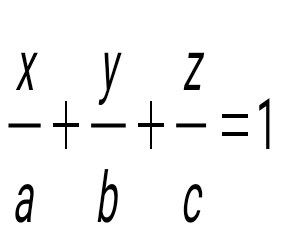
Нүктеден жазықтыққа дейінгі қашықтық қай формуламен есептелініледі:
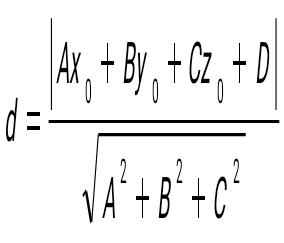
Екі |
 Скачать 1.82 Mb.
Скачать 1.82 Mb.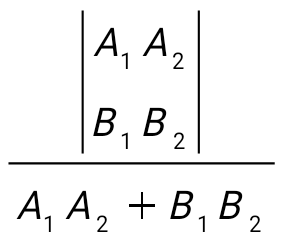 .
.