ПР3_5. Цель Изучить определения и формулы расчёта основных понятий комбинаторики (перестановки, размещения и сочетания) и научиться использовать их при решении типовых комбинаторных задач
 Скачать 97.3 Kb. Скачать 97.3 Kb.
|
|
(Где титульный лист?) Практическое задание №3 Перестановки, размещения и сочетания Цель: Изучить определения и формулы расчёта основных понятий комбинаторики (перестановки, размещения и сочетания) и научиться использовать их при решении типовых комбинаторных задач. ВАРИАНТ №1. Сколько различных «слов», состоящих не менее чем из четырех разных букв, можно образовать из букв слова ”ученик”: Слово УЧЕНИК состоит из 6-ти букв. По правилу произведения 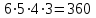 четырёхбуквенных слов, четырёхбуквенных слов, 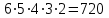 пятибуквенных и пятибуквенных и 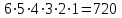 шестибуквенных слов. По правилу суммы всего можно составить шестибуквенных слов. По правилу суммы всего можно составить 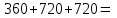 1 800 слов, состоящих не менее, чем из 4-х букв. 1 800 слов, состоящих не менее, чем из 4-х букв.Ответ: 1 800 слов. В магазине имеется 6 сортов шоколадных конфет и 4 сорта карамели. Сколько различных покупок конфет одного сорта можно сделать в этом магазине? Сколько можно сделать различных покупок, содержащих один сорт шоколадных конфет и один сорт карамели? По правилу суммы получаем, что можно сделать 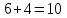 покупок конфет одного сорта, по правилу произведения покупок конфет одного сорта, по правилу произведения 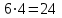 покупок, содержащих один сорт шоколадных конфет и один сорт карамели. покупок, содержащих один сорт шоколадных конфет и один сорт карамели. Ответ: 10 покупок; 24 покупки. Сколько можно получить различных четырехзначных чисел, вставляя пропущенные цифры в число *2*5? в число 3*7*? Между 2 и 5 можно вставить 10 цифр (от 0 до 9) Перед 2 можно вставить 9 цифр (от 1 до 9), т. к. число должно быть четырехзначным Всего 9 * 10 = 90 чисел (А вторую часть решать не надо?) У одного человека имеется 7 книг по математике, а у другого—9. Сколькими способами они могут осуществить обмен книги на книгу? Решение (А где же здесь обмен «книги на книгу»?) 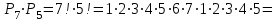 604 800. 604 800.Ответ: 604 800 способами. В букинистическом магазине продаются 6 экземпляров романа И. С. Тургенева «Рудин», 3 экземпляра романа «Дворянское гнездо» и 4 экземпляра романа «Отцы и дети». Кроме того, имеется 5 томов, состоящих из романов «Рудин» и «Дворянское гнездо», и 7 томов, состоящих из романов «Дворянское гнездо» и «Отцы и дети». Сколькими способами можно сделать покупку, содержащую по одному экземпляру каждого из этих романов? Сборник "Рудин" + "Дворянское гнездо" и отдельно "Отцы и дети". Всего 5*4 = 20 вариантов. 2) Сборник "Дворянское гнездо" + "Отцы и дети" и отдельно "Рудин". Всего 7*6 = 42 варианта. 3) Каждый роман отдельно. Всего 6*3*4 = 72 варианта. Итого 20 + 42 + 72 = 134 варианта. Имеется 4 чашки, 5 блюдец и 6 чайных ложек (все чашки, блюдца и ложки различные). Сколькими способами может быть накрыт стол для чаепития на трех человек, если каждый получит одну чашку, одно блюдце, одну ложку? Способов расставить 4 чашки: (размещения без повторений) 4*3*2=24 (А у Вас только три клиента. Поясните, что Вы делаете.) Способов расставить 5 блюдец: (размещения без повторений) 5*4*3=60 Способов расставить 6 ложек: (размещения без повторений) 6*5*4=120 Всего способов накрытия стола по правилу произведения 24*60*120=172800 Сколькими способами можно расставить 12 белых и 12 черных шашек на черных полях шахматной доски? Белые шашки можно расставить С 12 32 (Это как понимать?) способами. После выбора 12 полей для белых шашек остается 32-12=20 полей для черных шашек, на которые их можно поставить С 12 20 способами. Всего по правилу произведения С 12 32 С 12 20 способов. (Так подсчитайте.) Сколько можно построить различных прямоугольных параллелепипедов, если длина каждого его ребра может выражаться любым целым числом от 1 до 10? Длину параллелепипеда можно выбрать 10-тью способами, ширину параллелепипеда можно выбрать 10-тью способами, высоту параллелепипеда можно также выбрать 10-тью способами. Получаем общее количество способов: 10*10*10=1000 Значит число таких параллелепипедов равно 1000. (Где титульный лист? Оформляйте каждую работу отдельно.) Практическое занятие №4 Формула включений и исключений и бином Ньютона Цель: Изучить методику использования формулы включений и исключений для решения задач по определению количества элементов в множестве. Изучить методику разложения выражения 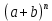 по формуле бинома Ньютона. по формуле бинома Ньютона.ВАРИАНТ №1. Из ста учеников девятых классов на первом экзамене получили отличные и хорошие оценки 80%, на втором экзамене - 72%, на третьем - 60%. Какое может быть наименьшее число учащихся, получивших отличные и хорошие оценки на всех трех первых экзаменах? На первом экзамене получили хор. оценки 100*0,8 = 80 учеников (множествоА) на втором 72 (множ-во Б) на третьем 60 (множ-во С) пусть во множество Б вошли 20 учеников плохо (Разве?) сдавших первый экзамен, и соответственно 52 человека которые сдали 1 и 2 экзамен хорошо. Таким образом, 20 учеников не сдали ни первый ни второй экзамен 52 сдали 1 и 2 экзамен 28 сдали хорошо только один из двух первых экзаменов. Пусть третьий экзамен сдали хорошо 20 человек не сдавших 1 и 2 (Это как понимать?) экзамен, 28 человек сдавших один из двух первых экзаменов (уже 48) и значит 12 человек сдавших и первый и второй экзамен хорошо. (Как получили?) Таким образом сдали все три экзамена на хорошо и отлично только 12 человек, а это 12% Каждый из учеников класса в зимние каникулы ровно два раза был в кинотеатре, при этом фильмы А, В, С видели соответственно 25,12 и 23 ученика. Сколько учеников в классе? Сколько из них видели спектакли А и В, А и С, В и С? Введем обозначения Пусть фильм A и B видели xAB учеников фильм A и С видели xAС учеников фильм B и C видели xBC учеников Тогда получаем xAB+xAC=25 (1) xAB+xBC=12(2) xAC+xBC=23 (3) xAB-xBC=2 (Поясните, это откуда?) xAB+xBC=12 xAC=23-xBC xAB=7 (Как получили?) xBC=5 xAC=18 всего в классе xAB+xBC+xAC=7+5+18=30 человек (Надо было пользоваться формулой «включения- исключения».) Практическая работа №5 Принцип математической индукции и рекуррентные соотношения Цель: Изучить принцип математической индукции и научиться использовать его для доказательства истинности утверждений занумерованных натуральными числами. Метод математической индукции Докажите методом математической индукции истинность следующих формул для любого натурального n. ВАРИАНТ №1 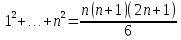 . . Проведём доказательство методом математической индукции. Обозначим А(n)=32n+1+2n+2. База индукции. Если n=1, то А(1)=33+23=35 и, очевидно, делится на 7. Предположение индукции. Пусть А(k) делится на 7. Индукционный переход. Докажем, что А(k+1) делится на 7, то есть справедливость утверждения задачи при n=k. А(k+1)=32(k+1)+1+2(k+1)+2=32k+1·32+2k+2·21=32k+1·9+2k+2·2= =32k+1·9+2k+2·(9–7)=(32k+1+2k+2)·9–7·2k+2=9·А(k)–7·2k+2. (Какое отношение это решение имеет к Вашему условию?) 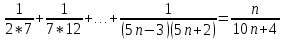 . .  (Какое отношение это решение имеет к Вашему условию?) Доказать, что при любом целом положительном n число n2+n является четным. n^2 + n = n(n + 1). Выражение представляет собой произведение двух последовательных целых чисел. Одно из них чётное, тогда и произведение является чётным. (Если n чётное, то условие выполнено. Если n нечётное, то следующее за ним (n + 1) непременно чётное) Список рекомендуемоЙ литературы Шевелев Ю. П. Дискретная математика. Учебное пособие - Спб.: Изд-во « Лань», 2008. Просветов Г. И. Дискретная математика : задачи и решения: учебное пособие. - М.: БИНОМ. Лаборатория знаний, 2008. Данилов В. Г., Дубнов В. Л., Лакерник А. Р., Райцин А. М. Дискретная математика. Учебное пособие для вузов. - М.: Горячая линия - Телеком, 2008. Андерсон Дж. Дискретная математика и комбинаторика. - М.; Спб., Киев: Вильямс, 2003. Кузнецов О. П. Дискретная математика для инженера. - СПб: Изд-во « Лань», 2005. |
