Курсовая. курсовая работа щелаков. Цель курсового проекта
 Скачать 165.57 Kb. Скачать 165.57 Kb.
|
 ВВЕДЕНИЕСистема автоматического управления (САУ) представляет собой комплекс программно-технических средств, реализованный в комплектном устройстве и предназначена для автоматизированного управления станком, машиной, агрегатом, линией. САУ может управлять электроприводами (сервоприводами), гидравликой, пневматикой. Актуальность курсового проекта заключается в закреплении и практическом применении полученных знаний для расчета и исследования системы автоматического регулирования. Цель курсового проекта – расчет и исследование системы автоматического регулирования. Задачи курсового проекта: дать понятие об устойчивости и о частотных критериях устойчивости систем автоматического регулирования; описать структурный состав заданной САР; рассчитать передаточные функции разомкнутой и замкнутой системы; построить временные и частотные характеристики системы; провести анализ устойчивости, разомкнутой и замкнутой систем; исследовать качество переходных процессов замкнутой системы автоматического регулирования. Объектом курсового проекта является система автоматического регулирования. Предмет курсового проекта – динамические свойства объекта. В результате выполнения курсового проекта реализовать следующие профессиональные компетенции (ПК): ПК 1.1. Осуществлять анализ имеющихся решений для выбора программного обеспечения для создания и тестирования модели элементов систем автоматизации на основе технического задания. ПК 1.2. Разрабатывать виртуальную модель элементов систем автоматизации на основе выбранного программного обеспечения и технического задания. ПК 1.3. Проводить виртуальное тестирование разработанной модели элементов систем автоматизации для оценки функциональности компонентов. ПК 1.4. Формировать пакет технической документации на разработанную модель элементов систем автоматизации. 1 ТЕОРЕТИЧЕСКАЯ ЧАСТЬ 1.1 Понятия об устойчивости. Для устойчивости линейной системы с характеристическим уравнением a0p3+a1p2+a2p+a3=0 необходимо выполнение двух условий: 1) все коэффициенты характеристического уравнения должны быть положительными; 2) произведение средних коэффициентов должно быть больше произведения крайних, т.е. a1a2> a0a3 Для определения устойчивости систем любого порядка применяют критерий Гурвица и критерий Рауса. По критерию немецкого математика Гурвица система будет устойчива, если определитель Гурвица, все его диагональные миноры и первый коэффициент характеристического уравнения a0 положительны т.е. a0>0; 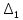 >0; >0; 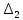 >0; …; >0; …; 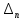 >0. (1) >0. (1)Определитель Гурвица строится по коэффициентам характеристического уравнения.  (2) (2)По главной диагонали определителя слева на право выписываются все коэффициенты характеристического уравнения от a1 до an, в порядке возрастания индексов. Столбцы вверх от главной диагонали дополняют коэффициентами характеристического уравнения с последовательно возрастающими индексами. А столбцы вниз - коэффициентами с последовательно убывающими индексами. Максимальный индекс коэффициента n (n - порядок характеристического уравнения), минимальный - нуль. Столбец заполняется до положенного числа n элементов нулями. Отмечая в определителе Гурвица диагональные миноры, получим определители низшего порядка 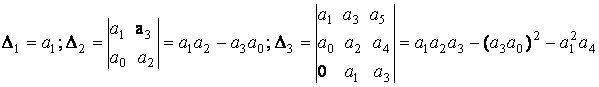 (3) (3)Номер диагонального минора определяется номером коэффициента по диагонали, для которого составляется минор. Исследуя с помощью критерия Гурвица устойчивость систем первого, второго, третьего и более высоких порядков, можно сделать вывод: для системы n – го порядка необходимым условием устойчивости является положительность всех коэффициентов. 1.2 Показатели качества переходного процесса замкнутой системы регулирования После обеспечения устойчивости системы необходимо обеспечить качество переходного процесса управления, которое оценивают по переходной функции h(t), представляющей собой реакцию системы на внешнее воздействие типа единичной ступенчатой функции 1(t). На примере переходной функции, представленной на рисунке 1, рассмотрим основные показатели качества переходного процесса –времярегулирования, перерегулирование, частотуколебаний, числоколебаний, максимальнуюскорость и максимальное ускорение регулируемой величины.  Рисунок 1 – Основные показатели качества Время регулирования tp определяется длительностью переходного процесса. Теоретически переходной процесс длится бесконечно долго, однако практически он заканчивается, как только отклонения регулируемой величины от нового ее установившегося значения не будут превышать допустимых пределов. Обычно принимают e=(3/5)%Hуст. Временем регулирования характеризуют быстродействие системы. Однако иногда быстродействие также характеризуют временем ty достижения переходной функцией первый раз нового установившегося значения или временем tmax достижения максимального значения hmax. Перерегулирование ∆hmax или выброс, представляет собой максимальное отклонение регулируемой величины от нового установившегося значения. Обычно первый максимум является наибольшим. Относительное перерегулирование, 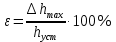 . (4) . (4)Время регулирования hmax и перерегулирование (основные показатели переходного процесса) тесно связаны между собой. Перерегулирование появляется вследствие того, что система к новому установившемуся состоянию подходит с определенной скоростью, которая графически отображается тангенсом угла наклона касательной в точке А. 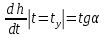 . (5) . (5)Чем больше эта скорость, тем дальше за новое установившееся положение «пройдет» система по инерции. Для уменьшения перерегулирования необходимо снизить скорость, с которой система подходит к новому установившемуся состоянию. Это приводит к увеличению времени регулирования. Если система подходит к новому установившемуся состоянию с нулевой скоростью, то перерегулирования не происходит, но время регулирования значительно возрастает. Таким образом, отсутствие и очень большое перерегулирование нежелательны. Поэтому перерегулирование допускают в пределах 20 – 30 % установившегосязначения. Приэтомчислополуколебанийпереходнойфункции 1.3 Описание структурного состава заданной САУ На рисунке (2) показана система автоматического регулирования, в соответствии с которой проводился расчёт и исследование.                      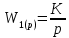 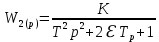 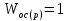 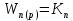 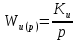       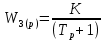 Рисунок 2 - Структурная схема системы автоматического регулирования САУ состоит из ПИ-регулятора и идеального интегрирующего, колебательного и апериодического звена первого порядка. Пропорционально-интегральный регулятор представляет собой параллельное соединение пропорционального, интегрирующего звена. Передаточная функция ПИ-регулятора имеет вид: 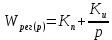 , (6) , (6)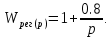 Идеальное интегрирующее звено охвачено единичной обратной связью и имеет следующую передаточную функцию: 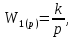 (7) (7)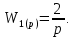 Колебательное звено параллельно звену запаздывания и имеет следующую передаточную функцию: 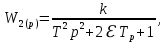 (8) (8)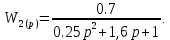 Апериодическое звено первого порядка и колебательное звено, параллельно идеальному интегрирующему звену, охваченному единичной обратной связью, звено запаздывания имеет следующую передаточную функцию: 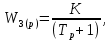 (9) (9)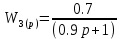 Система имеет замкнутую структуру, т.к. она охвачена отрицательной обратной связью. 2 РАСЧЕТНАЯ ЧАСТЬ 2.1 Расчет передаточной функции разомкнутой и замкнутой системы Произведем расчет передаточной функции разомкнутой системы автоматического регулирования, состоящей из идеального интегрирующего звена, охваченного обратной связью, колебательного звена, апериодического звена первого порядка, а также ПИ регулятора. Расчет передаточной функции идеального интегрирующего звена, охваченного обратной связью будет иметь вид: 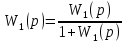 , (10) , (10)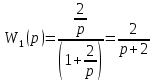 . .Идеально-интегрирующее звено, охваченное обратной связью, параллельно соединено с колебательным звеном, следовательно, передаточная функция будет иметь вид: 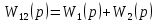 , (11) , (11)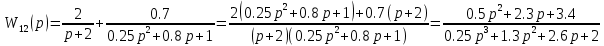 . .Идеально-интегрирующее звено, охваченное обратной связью, и колебательное звено параллельно соединены с апериодическое звеном первого порядка, следовательно, передаточная функция будет иметь вид: 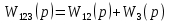 , (12) , (12)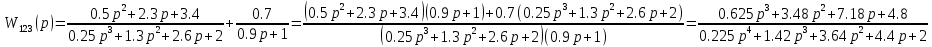 . .Зная, что разомкнутая система, включает в себя ПИ регулятор, произведем расчет разомкнутой системы: 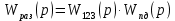 , (13) , (13)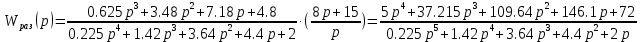 . .Зная передаточную функцию разомкнутой системы, а также наличие обратной связи, произведем расчет замкнутой системы: 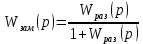 , (14) , (14)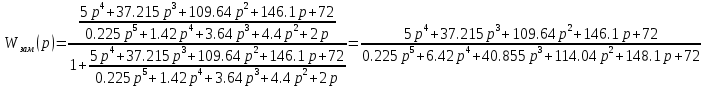 . .Первоначальная задача расчета САР сводится к определению ее передаточной функции, так как передаточная функция системы полностью определяет ее динамические свойства. 2.2 Определение и построение временных характеристик исследуемой системы Временные характеристики систем автоматического регулирования представляют собой переходные и импульсные переходные функции, и их графики, отражают зависимость изменения выходной величины системы от времени при подаче на ее вход единичного воздействия при нулевых начальных условиях. Исследуем переходную характеристику заданной САР с помощью программы MathCAD, ее обозначают через h(t), она имеет вид: 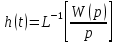 ,(15) ,(15)где 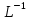 обратное преобразование Лапласа. обратное преобразование Лапласа.Найдем переходную характеристику использую в качестве передаточной функции передаточную функцию разомкнутой системы (Wраз). Переходная характеристика исследуемой системы определяется по формуле 15 и равна: 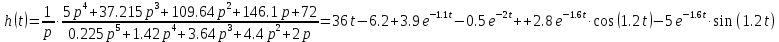 . .График изменения переходной характеристики по времени изображен на рисунке 2, и построенспомощьюпрограммы MathCAD, имеетследующийвид: 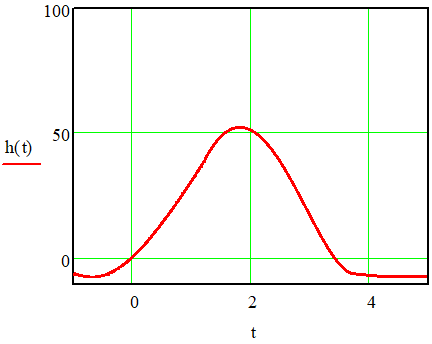 Рисунок 2 –Временнаяпереходнаяхарактеристика Импульсная переходная характеристика равна:  , (16) , (16)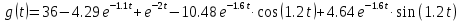 , ,график представлен на рисунке 3: 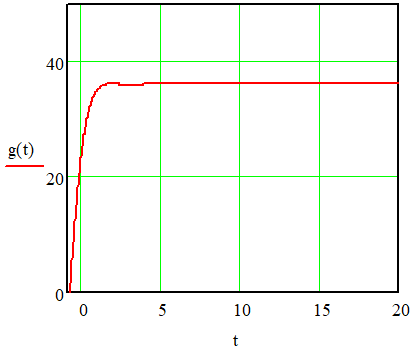 Рисунок 3 –Импульсная переходная характеристика Временные переходные характеристики определяют реакцию звена САР на возмущения произвольного вида и являются динамическим описанием свойств системы. 2.3 Определение и построение частотных характеристик исследуемой системы Частотные характеристики отображают изменение амплитуды и фазы выходной функции системы относительно синусоидального входного воздействия в установившемся режиме при изменении частоты. Для того чтобы определить частотные характеристики данной системы, построим графики амплитудно-частотной характеристики и фаза-частотной характеристики с помощью MathCAD. Для начала зададим диапазон изменения частоты 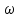 : :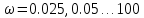 . (17) . (17)Далее определим комплексную переменную: 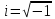 . (18) . (18)Выполним замену оператору Лапласа: 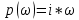 . (19) . (19)Зададим расчетное выражение передаточной функции с использованием определенной переменной p. 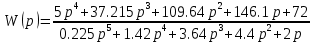 . .Определим выражения частотных характеристик. Выделим действительную и мнимую части выражения: 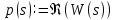 , (20) , (20)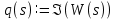 . (21) . (21)Взятие модуля выражения: 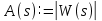 . (22) . (22)Взятие аргумента выражения в радианах: 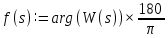 . (23) . (23)Получим график АЧХ, представленный на рисунке 4: 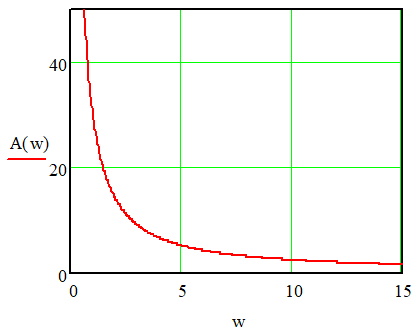 Рисунок 4 –Амплитудная частотнаяхарактеристика Получим график АФЧХ, представленный на рисунке 5: 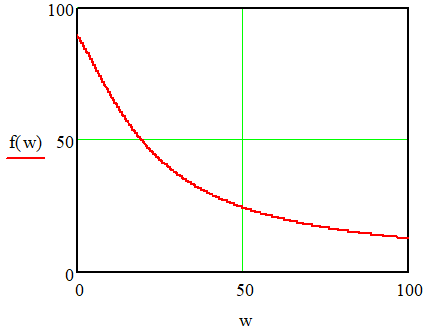 Рисунок 5 – Фазовая частотная характеристика АЧХ на некоторой частоте указывает, во сколько раз амплитуда сигнала этой частоты на выходе системы отличается от амплитуды выходного сигнала на другой частоте. ФЧХ показывает изменение частоты заданной системы во времени. 2.4 Проверка устойчивости системы по алгебраическому критерию Рауса-Гурвица Для того чтобы динамическая система была устойчивой, необходимо чтобы все коэффициенты характеристического уравнения были положительны. Критерий Рауса - Гурвица позволяет определить положении корней характеристического уравнения на комплексной плоскости, а, следовательно, говорит об устойчивости системы, не решая характеристического уравнения. Для определения устойчивости заданной системы по алгебраическому критерию Рауса-Гурвица, воспользуемся характеристическим уравнением разомкнутой системы: 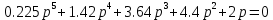 . .По характеристическому уравнению, составим определитель Гурвица и рассчитаем определители 1-5 порядков: 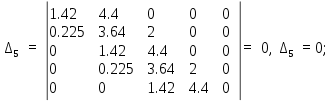 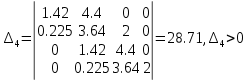 ; ;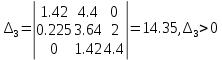 ; ;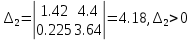 ; ;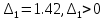 . .Так как значения определителей 1 - 4 порядка больше нуля, а определитель пятого порядка равен нулю, можно сказать, что исследуемая система находится на границе апериодической устойчивости. 2.5 Проверка устойчивости системы по частотным критериям Михайлова и Найквиста Выполним проверку устойчивости по частотным критериям. Построим годограф Михайлова по передаточной функции системы с помощью программы MathCad: 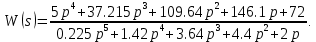 Возьмем характеристическое уравнение системы, зададим диапазон изменения частоты: 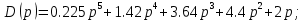  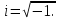 Получим годограф Михайлова, представленный на рисунке 6. 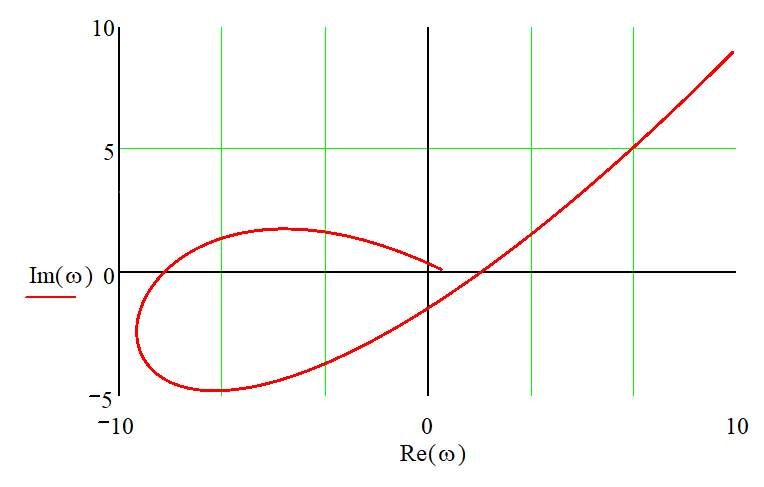 Рисунок 6 - ГодографМихайлова Из графика видно, что годограф Михайлова при изменении частоты от 0 до ∞, начинается на вещественной положительной полуоси, обходит против часовой стрелки последовательно 5 квадрантов координатной плоскости, не обращаясь в ноль. Условие устойчивости выполняется, система устойчива. Для проверки критерия устойчивости по критерию Найквиста построим АЧХ исследуемой системы. Для этого соберем схему САУ в программе VisSim, как показано на рисунке 7. 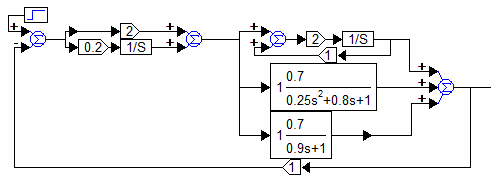 Рисунок 7 - Структурная схема САР в VisSim Получим график критерия устойчивости Найквиста, представленный на рисунке 8. 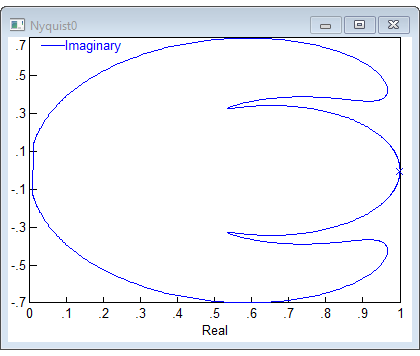 Рисунок 8 - Графиккритерияустойчивости Найквиста По полученному графику можно сказать, что система устойчива, так как АЧХ не охватывает точку с координатами (-1; j0) 2.6 Исследование качества переходного процесса замкнутой системы регулирования Качество регулирования представляет собой совокупность точности в установившемся режиме и качества переходных процессов. Построим схему исследуемого процесса в программе VisSim и получим график переходного процесса, представленный на рисунке 9. 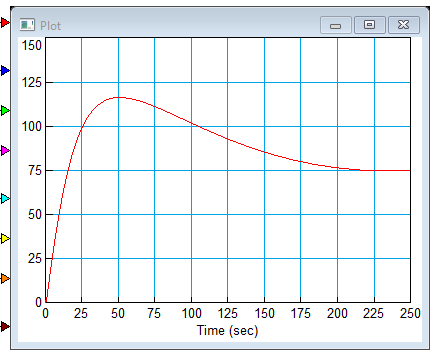 Рисунок 9 - ПереходныйпроцессисследуемойСАР Из графика видно, что характер переходного процесса затухающий колебательный, система устойчива. Время регулирования составляет 215 секунд. Для оценки качества с помощью интегрально-квадратичной оценки соберем схему согласно рисунку 10. 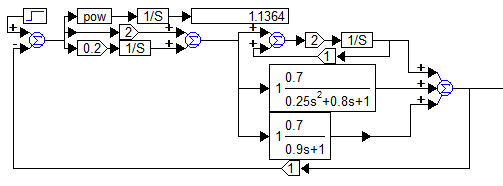 Рисунок 10 –Схемаполученияинтегральноквадратичнойоценки Промоделировав данную схему, получим величину интегрально-квадратичной оценки. Она равна 1.1364. Величина интегрально-квадратичной оценки достаточно мала. Качество переходного процесса удовлетворительно. ЗАКЛЮЧЕНИЕ В курсовом проекте на тему «Расчет и исследование системы автоматического регулирования, состоящей из идеального интегрирующего, колебательного и апериодического звена первого порядка с ПИ-регулятором» проведен расчет и исследование системы автоматического регулирования. В теоретической части курсового проекта дано понятие об устойчивости, о показателях качества переходного процесса замкнутой системы регулирования, описан структурный состав заданной САР. В расчетной части произведен расчет передаточных функций разомкнутой и замкнутой системы, поострены временные и частотные характеристики системы, проведен анализ устойчивости, разомкнутой и замкнутой систем, исследовано качество переходных процессов замкнутой системы автоматического регулирования. В ходе выполнения курсового проекта реализованы следующие профессиональные компетенции (ПК): ПК 1.1, ПК 1.2, ПК 1.3, ПК 1.4. Список использованных источников 1. Андреев С.М. Разработка и моделирование несложных систем автоматизации учетом специфики технологических процессов: учеб. пособие для студ. учреждений сред. проф. образования/ С.М. Андреев, Б.Н. Парсункин. - М.: Издательский центр «Академия», 2016. - 272 с. 2. Бородин И.Ф. Автоматизация технологических процессов и системы автоматического управления: учебник для СПО/ И.Ф. Бородин, С.А. Андреев. - 2 -е изд., испр. и доп. - М.: Издательство Юрайт, 2019. -386с. 3. Молоканова Н.П. Автоматическое управление. Курс лекций с решением задач и лабораторных работ: учебное пособие/ Н.П. Молоканова. - М.: Форум, 2017. - 224с. 4. Советов Б.Я. Моделирование систем / Б. Я. Советов, С. А. Яковлев- М.: Высшая школа, 2015. - 343 с. 5. Понятие об устойчивости[Электронный ресурс]: http://stellus.rgotups.ru/exec/learning_materials. 6. Показатели качества переходного процесса [Электронный ресурс]: http://stellus.rgotups.ru/exec/learning_materials. 7. Проверка устойчивости по критериям Михайлова и Найквиста [Электронный ресурс]: https://studme.org/246765/kriteriy_ustoychivosti_naykvista. |
