Моделирование систем. Цель работы Освоить программную реализацию имитационной модели нелинейной динамической системы. Исходные данные
 Скачать 0.83 Mb. Скачать 0.83 Mb.
|
|
Цель работы Освоить программную реализацию имитационной модели нелинейной динамической системы. Исходные данные Модель – система уравнений 5-ого порядка представлена на рисунке 1. Исходные данные – на рисунке 2. 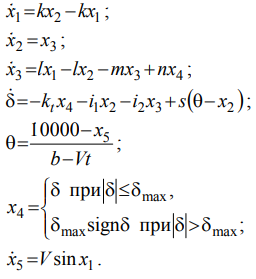 Рисунок 1 - Модель нелинейной динамической системы  Рисунок 2 – Исходные данные Задачи работы В соответствии с индивидуальным вариантом задания разработать и отладить программное приложение, обеспечивающее: 1. Решение системы дифференциальных уравнений на интервале [0; T] для T = 12 c с любым шагом, задаваемым пользователем в пределах (0; T). Для демонстрации результатов обеспечить вывод графиков xi(t), i=1, 2, …, n; значения указанной в задании переменной состояния в конце интервала интегрирования xk(T) и значения относительной погрешности его определения . 2. Анализ зависимости точности и трудоемкости решения задачи от шага интегрирования. Вывод графиков зависимостей относительной погрешности и оценки трудоемкости от величины шага h. 3. Автоматический выбор величины шага интегрирования для достижения относительной погрешности не более 1% с выводом итоговых результатов, перечисленных в п. 1, для найденного шага. Теоретические сведения Модель нелинейной динамической системы рассматривается в форме системы нелинейных нестационарных уравнений первого порядка представленной на рисунке 3.  Рисунок 3 – Система нелинейных нестационарных уравнений в общем виде При заданных начальных значениях переменных состояния xi(0)=xi(0), i=1, 2, …, n, путем интегрирования системы (1) могут быть определены законы их изменения во времени на любом требуемом интервале [0; T]. Системы нелинейных нестационарных уравнений, как правило, не поддаются аналитическому решению. Для их решения применяются приближенные (численные) методы. Спектр таких методов и реализующих их программных средств достаточно широк, но для изучения принципов и особенностей их применения в рамках данной лабораторной работы достаточно ограничиться методом Рунге–Кутта 1-го порядка (также именуемого методом Эйлера или методом прямоугольников). При этом программная реализация метода должна быть выполнена самостоятельно. Метод предусматривает решение уравнений в дискретном времени на основе преобразования модели (1) в рекуррентные соотношения (рисунок 4):  Рисунок 4 – Рекуррентные соотношения Точность решения, получаемого приближенными численными методами, повышается с уменьшением шага интегрирования, но при этом очевидно возрастает вычислительная трудоемкость решения задачи – количество шагов вычислений J и требуемое машинное время, а возможно, и объем используемой памяти компьютера при необходимости сохранения всего получаемого решения. Для моделей высокого порядка необоснованное уменьшение шага h может приводить к чрезмерному или недопустимому завышению требуемых ресурсов ЭВМ. Поэтому при реализации таких моделей вопрос выбора шага интегрирования для каждой модели требует отдельного решения с учетом необходимой точности получения результата и располагаемых вычислительных ресурсов. Выбор и обоснование величины шага интегрирования обычно возлагают на лицо, проводящее моделирование. Известны два основных подхода к контролю точности решения систем дифференциальных уравнений путем пошагового численного интегрирования. Первый предусматривает контроль точности в процессе интегрирования с уточнением величины каждого шага (контроль погрешности на шаге), второй – использование постоянной величины шага для всего интервала интегрирования и оценку погрешности по значениям переменных состояния только на правой границе интервала интегрирования t=T. В случае недопустимой величины погрешности процесс интегрирования повторяется с уменьшением величины шага. В рамках данной лабораторной работы предусматривается использование второго подхода с контролем точности по конечному значению одной из переменных состояния модели y=xk(T), указанной в индивидуальном варианте задания. Для оценки погрешности вычисления y с некоторым шагом h интегрирование повторяется с шагом h/2. Полученное с уменьшенным шагом значение y* принимается за эталонное. Тогда абсолютная погрешность вычисления y определяется как 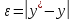 , относительная погрешность , относительная погрешность 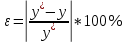 (4) (4) Для автоматизации выбора шага интегрирования в рамках данной лабораторной работы предусматривается использование следующего алгоритма: 1. Задается исходное значение шага интегрирования h. 2. Проводится решение системы дифференциальных уравнений на интервале [0; T] с шагом h. 3. Решение повторяется с шагом h/2. 4. Проводится оценка погрешности по соотношению (4). 5. Если погрешность не превышает допустимого значения, шаг h, считается достаточным для обеспечения требуемой точности. В противном случае в качестве нового проверяемого значения шага h принимается h/2 и производится переход к п. 3. Таким образом обеспечивается последовательное уменьшение шага интегрирования в 2m (m=1, 2, …) раз до достижения требуемой точности решения. Ход выполнения работы Разработанное решение представляет собой десктопной приложение на языке C# с применением технологии Windows Forms. Решение основной задачи представлено в файле Euler.cs (листинг 1), реализующем касс Euler. Связь с пользовательским интерфейсом описана в файле Forms1.cs (листинг 2). Решение системы дифференциальных уравнений на интервале [0; 12] с шагом h=0.01 представлено на рисунках 5-9. 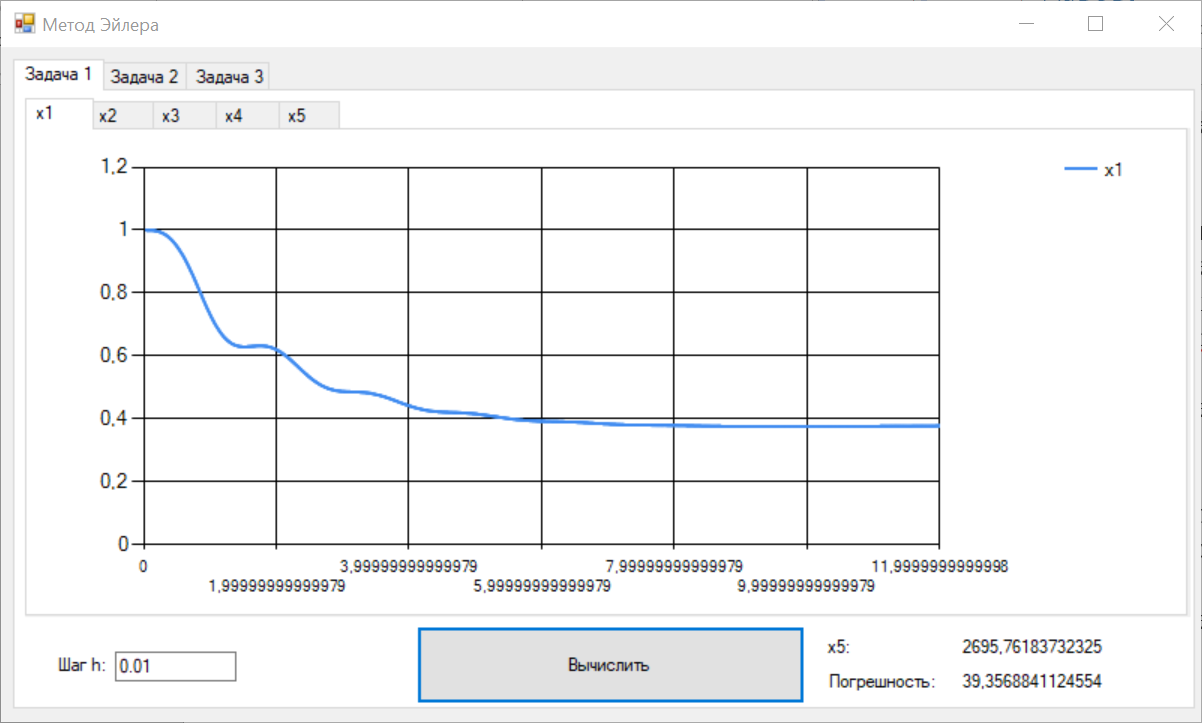 Рисунок 5 – Значения x1 при шаге h = 0.01 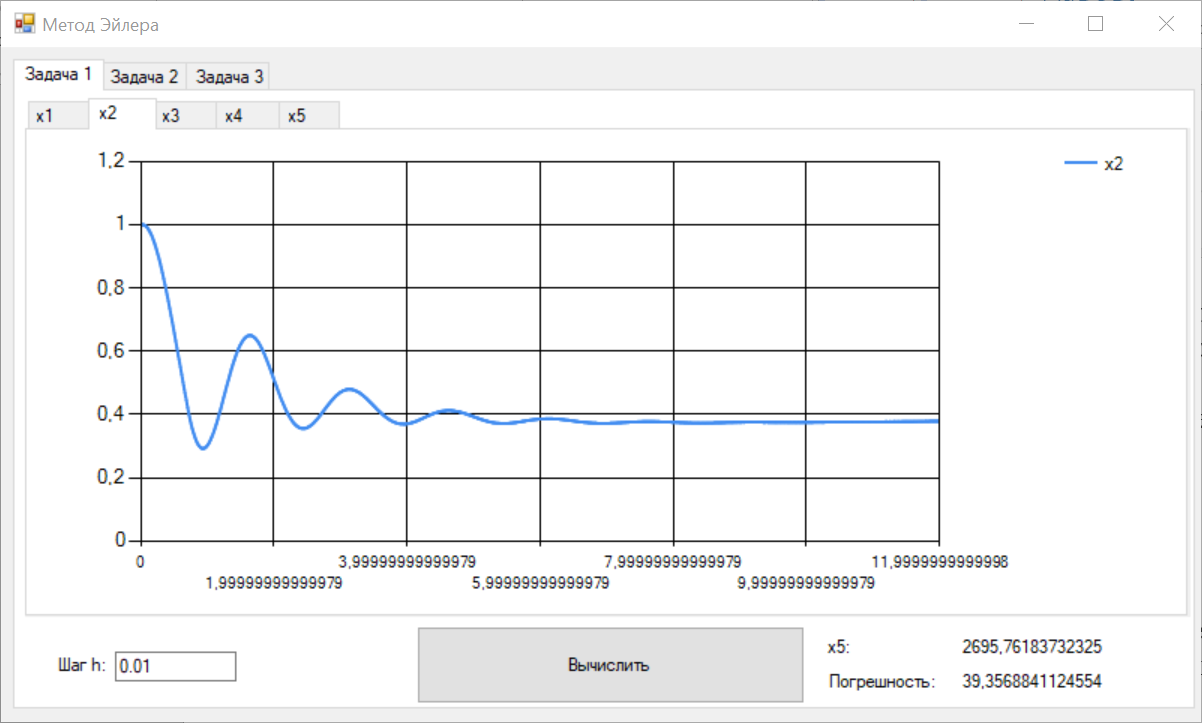 Рисунок 6 – Значения x2 при шаге h = 0.01 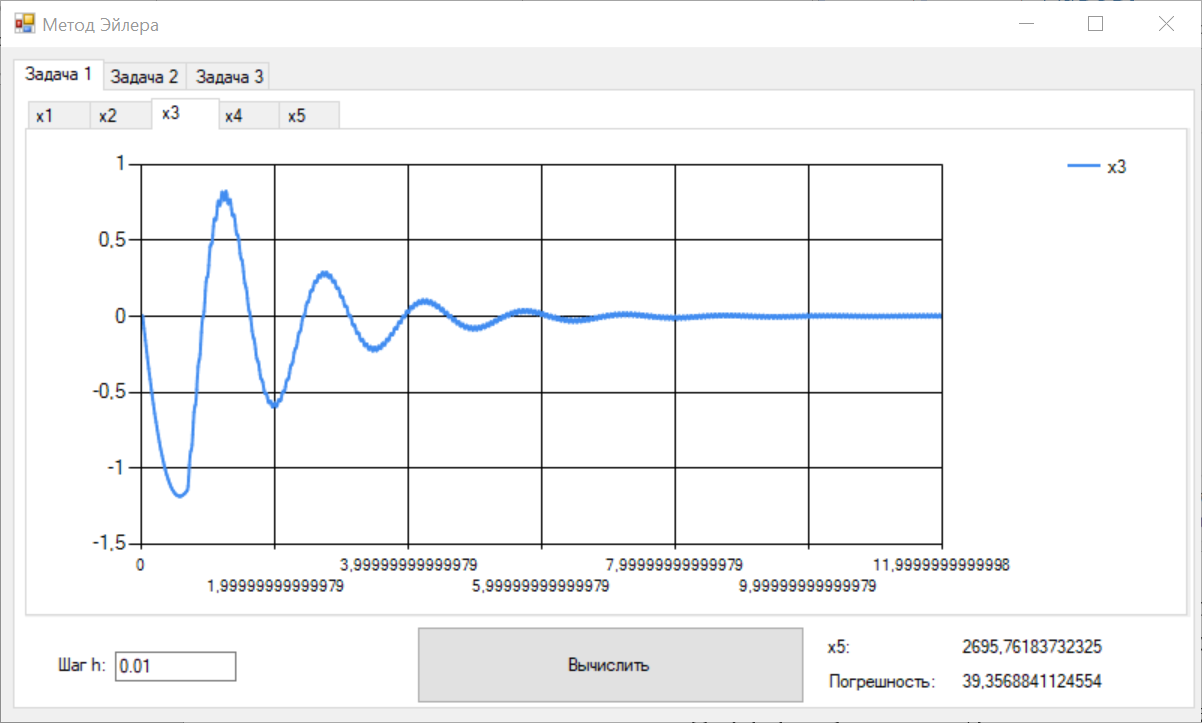 Рисунок 7 – Значения x3 при шаге h = 0.01 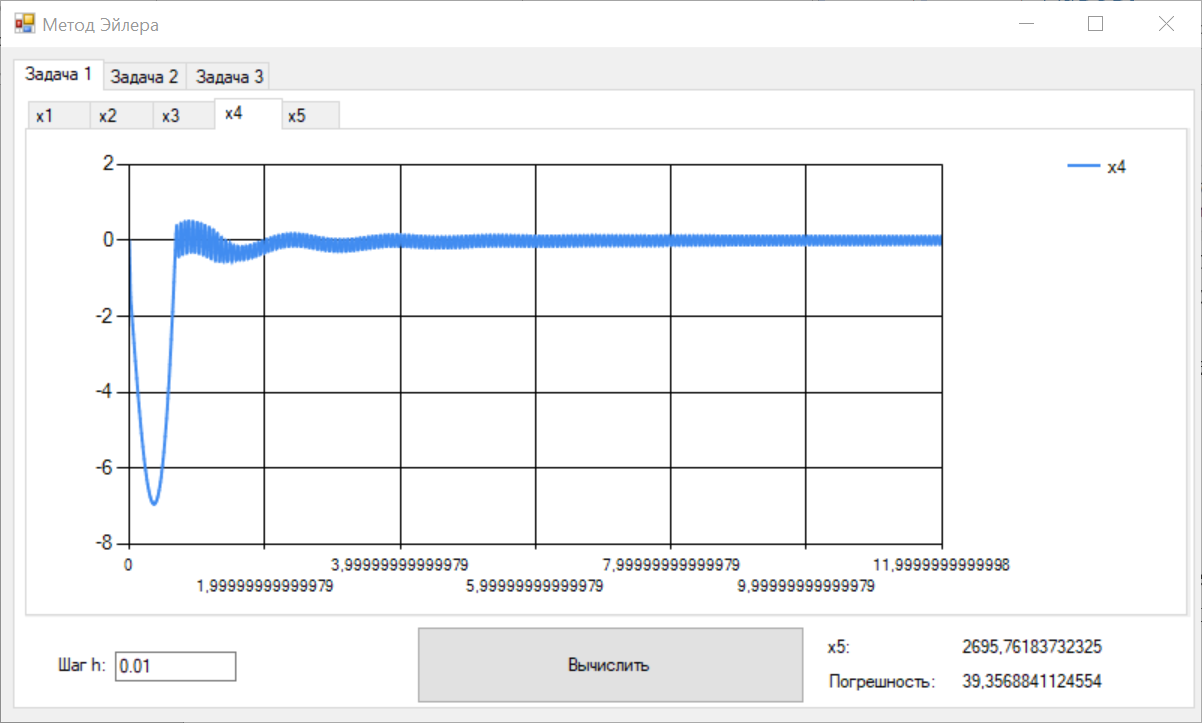 Рисунок 8 – Значения x4 при шаге h = 0.01 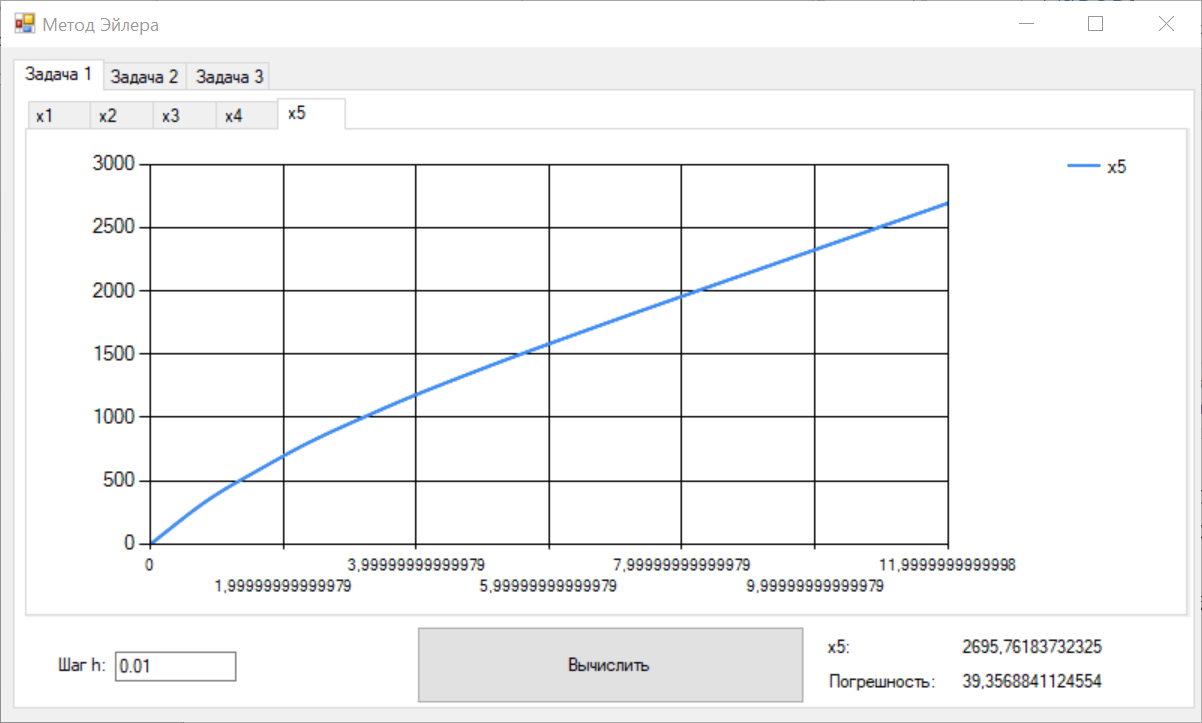 Рисунок 9 – Значения x5 при шаге h = 0.01 Анализ зависимости точности и трудоемкости решения задачи от шага интегрирования продемонстрирован на рисунках 10 и 11 соответственно. 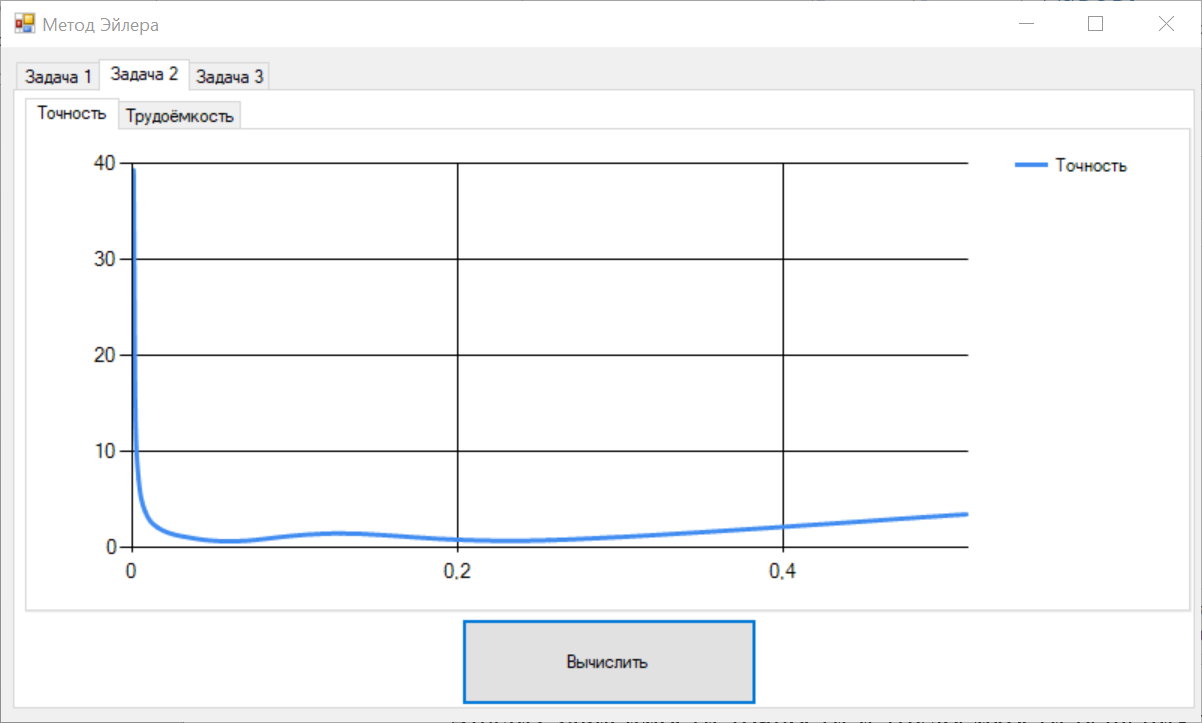 Рисунок 10 – Зависимость точности от шага на диапазоне h от 0.01 до 1 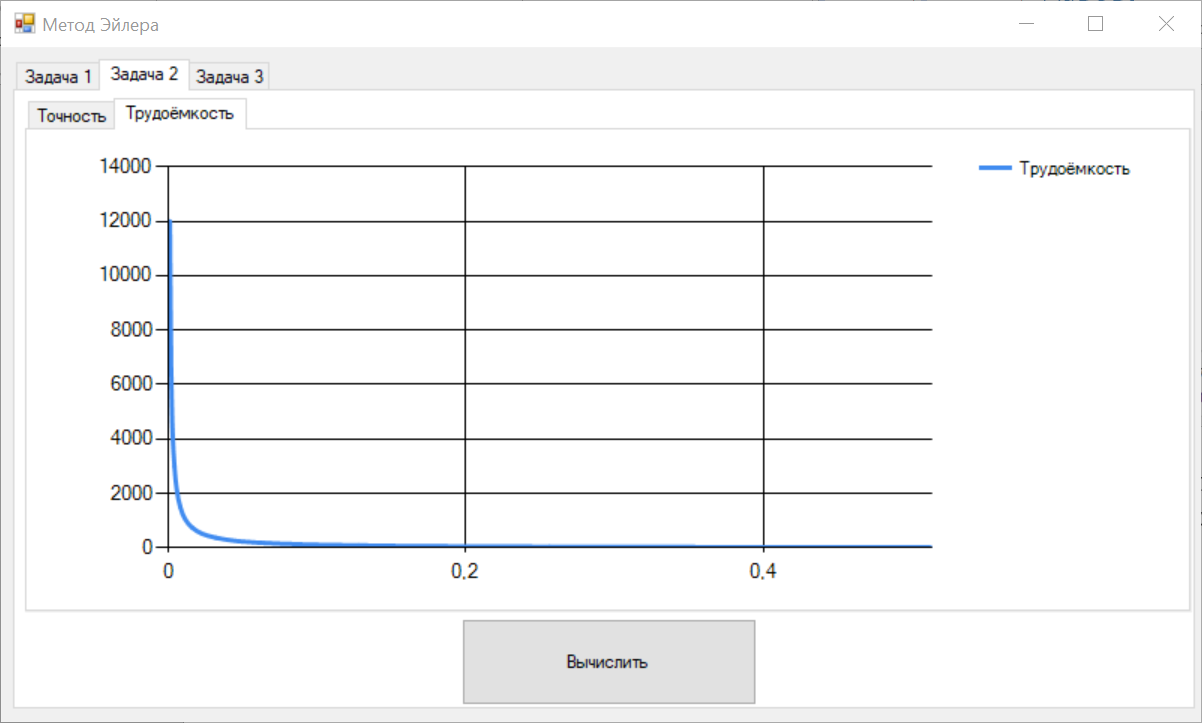 Рисунок 11 – Зависимость трудоёмкости от шага на диапазоне h от 0.01 до 1 Решение системы дифференциальных уравнений на интервале [0; 12] с автоматическим выбором шага и начальным значением шага h=0.01 представлено на рисунках 12-16. 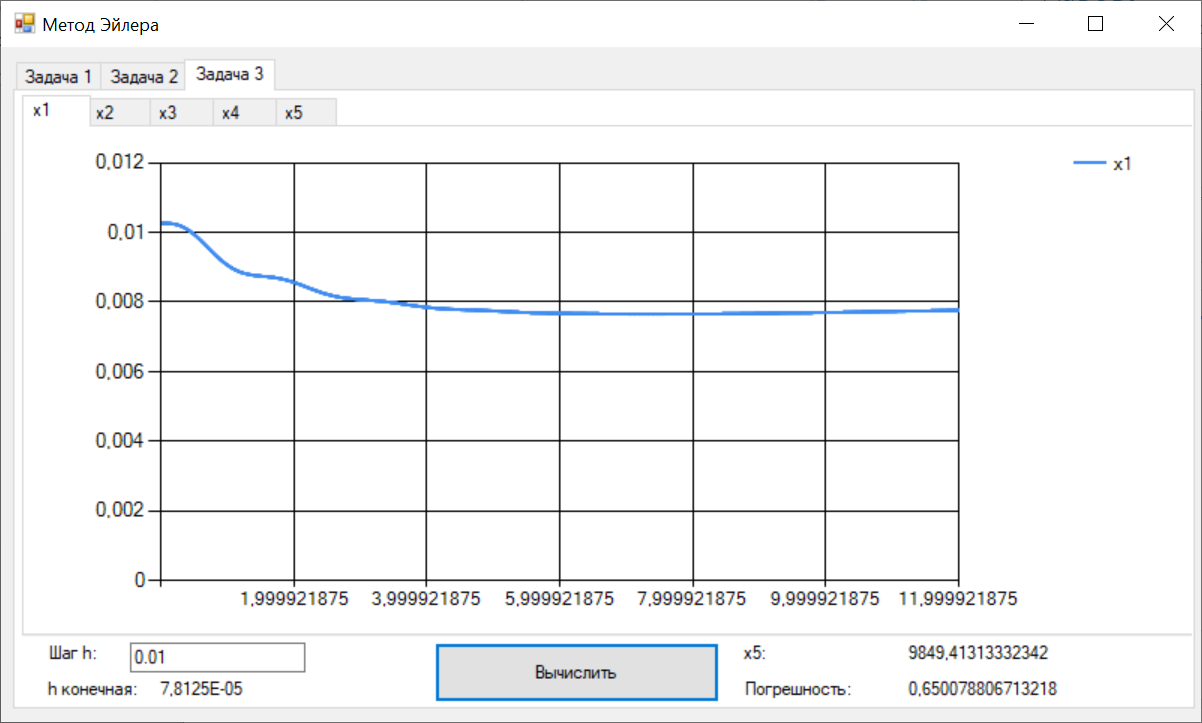 Рисунок 12 – Значения x1 при шаге h = 7,8125E-05 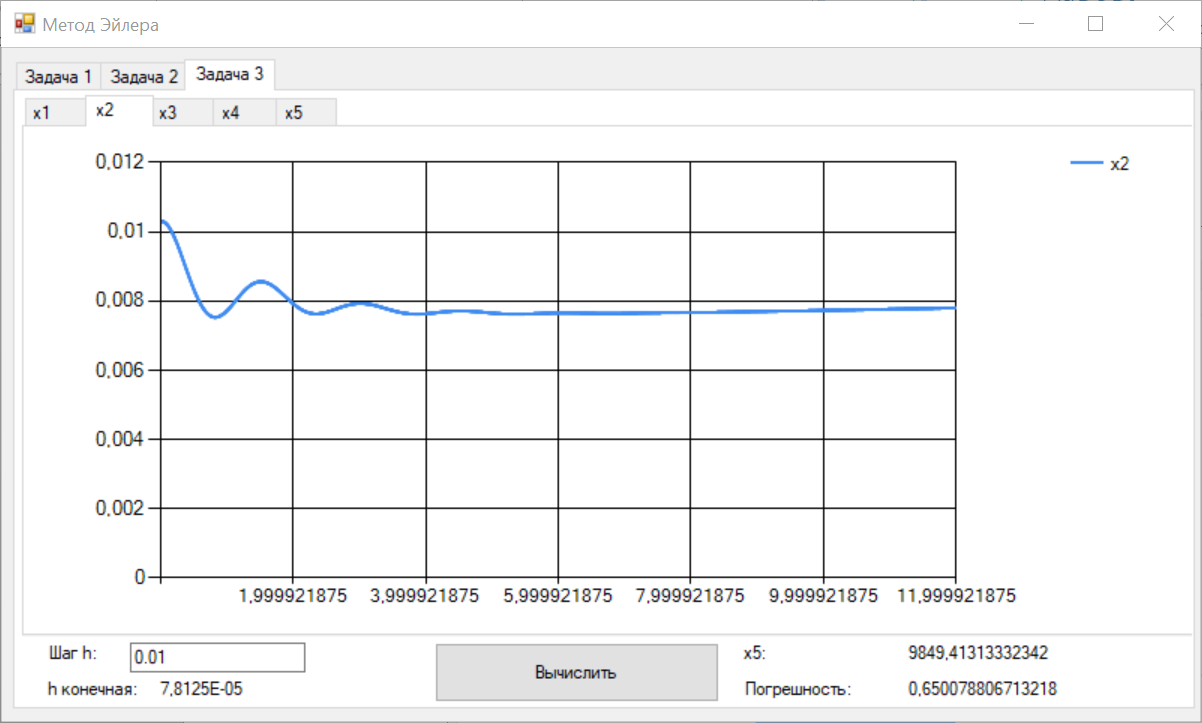 Рисунок 13 – Значения x2 при шаге h = 7,8125E-05 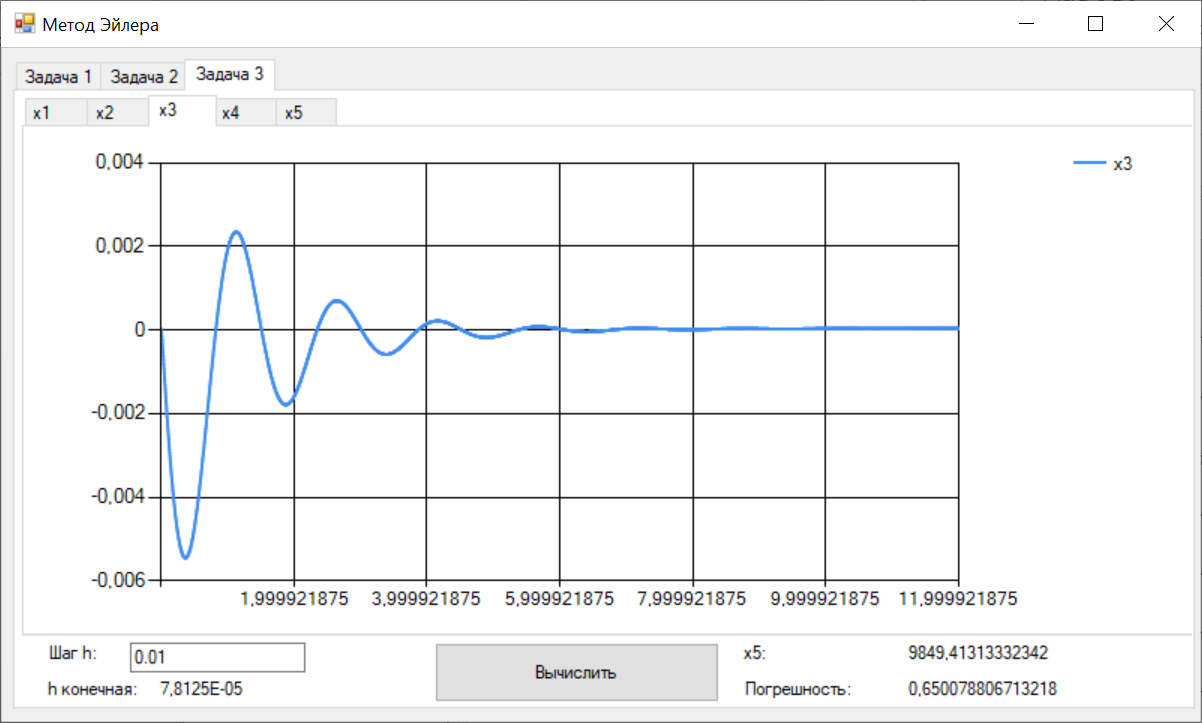 Рисунок 14 – Значения x3 при шаге h = 7,8125E-05 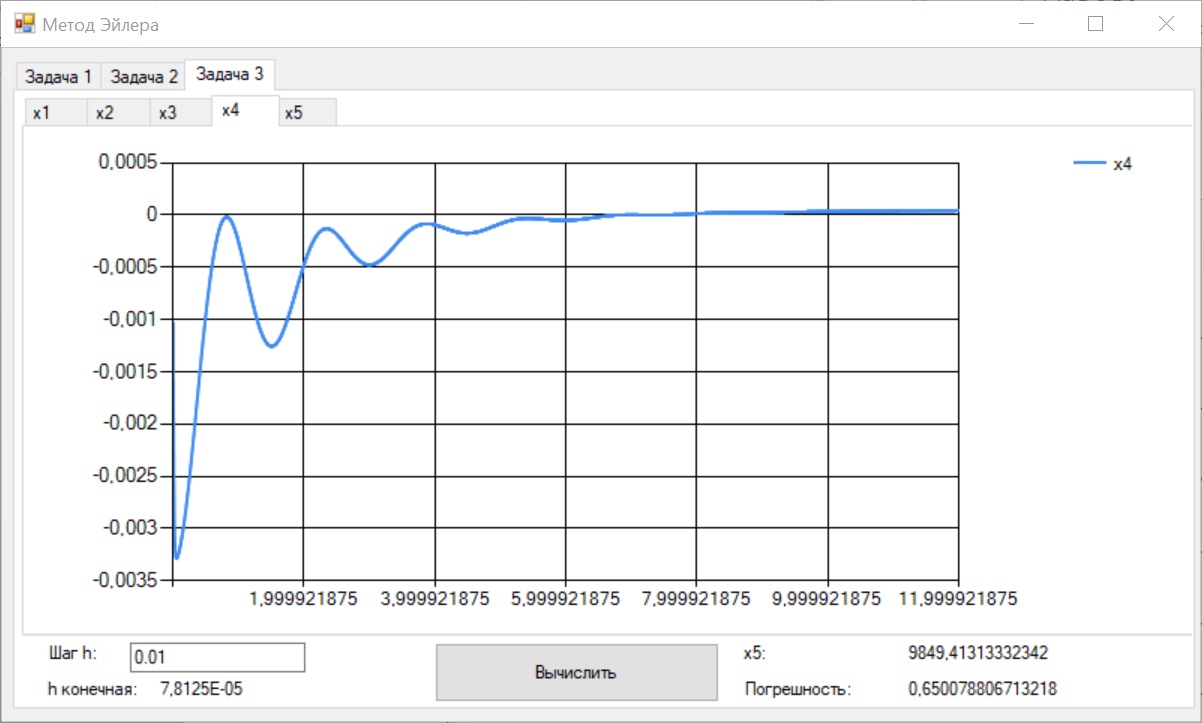 Рисунок 15 – Значения x4 при шаге h = 7,8125E-05 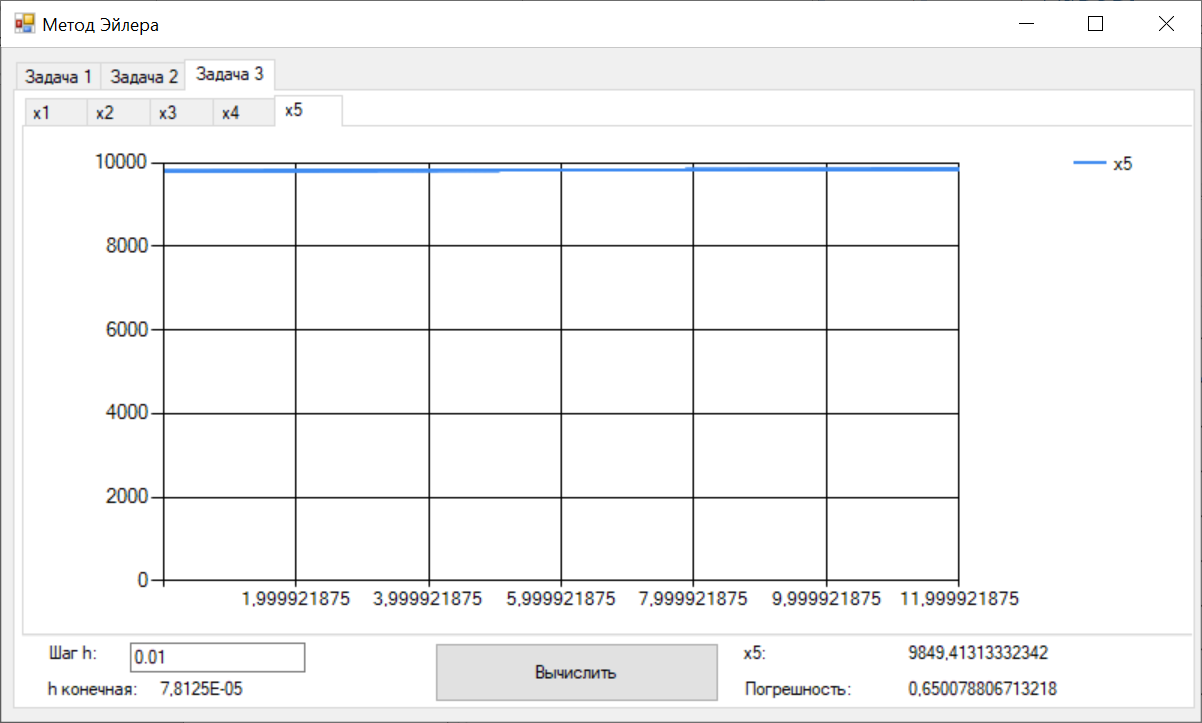 Рисунок 16 – Значения x5 при шаге h = 7,8125E-05 Листинг__1_–_Ф_айл__Euler.cs'>Листинг 1 – Файл Euler.cs using System; using System.Collections.Generic; namespace Method_Euler { class Euler { double[] xLast = { 1, 1, 0, 0, 0 }; // Метод Эйлера private double[] Eul(double[] xLast, double[] x, double h) { double[] res = new double[xLast.Length]; for (int i = 0; i < xLast.Length; i++) { res[i] = xLast[i] + x[i] * h; } return res; } // Решение систему дифференциальных уравнений с возвратом матрицы всех промежуточных решений public Dictionary { double[] xNext = new double[5]; double teta, x4; Dictionary for (double t = 0; t < T; t += h) { result.Add(t, xLast); // Добавление нового значения в новый момент времени в словарь результатов x4 = (Math.Abs(deltaLast) <= deltaMax) ? deltaLast : deltaMax * Math.Sign(deltaLast); teta = (10000 - xLast[4]) / (b - V * t); deltaLast = xLast[3]; xNext[0] = k * xLast[1] - k * xLast[0]; xNext[1] = xLast[2]; xNext[2] = l * xLast[0] - l * xLast[1] - m * xLast[2] + n * x4; xNext[3] = -kt * x4 - i1 * xLast[1] - i2 * xLast[2] + s * (teta - xLast[1]); xNext[4] = V * Math.Sin(xLast[0]); xLast = Eul(xLast, xNext, h); } result.Add(T, xLast); return result; } // Решение систему дифференциальных уравнений с возвратом конечного значения x5 public double getOnlyResult(double h, int k = 1, int l = 8, int m = 1, int n = 8, int kt = 100, int b = 22000, int i1 = 20, int i2 = 2, int s = 100, int V = 500, int T = 12, double deltaMax = 0.5d, double deltaLast = 0.0d) { double[] xNext = new double[5]; double teta, x4; for (double t = 0; t < T; t += h) { x4 = (Math.Abs(deltaLast) <= deltaMax) ? deltaLast : deltaMax * Math.Sign(deltaLast); teta = (10000 - xLast[4]) / (b - V * t); deltaLast = xLast[3]; xNext[0] = k * xLast[1] - k * xLast[0]; xNext[1] = xLast[2]; xNext[2] = l * xLast[0] - l * xLast[1] - m * xLast[2] + n * x4; xNext[3] = -kt * x4 - i1 * xLast[1] - i2 * xLast[2] + s * (teta - xLast[1]); xNext[4] = V * Math.Sin(xLast[0]); xLast = Eul(xLast, xNext, h); } return xLast[4]; } } } Листинг 2 – Файл Form1.cs using System; using System.Collections.Generic; using System.Windows.Forms; namespace Method_Euler { public partial class Form1 : Form { double T = 12; // Рассматриваемый временной период public Form1() { InitializeComponent(); } private void button1_Click(object sender, EventArgs e) { // Список объектов графиков var charts = new List // Предварительная очистка холстов графиков foreach (var chart in charts) { chart.Series[0].Points.Clear(); } double h = double.Parse(textBox1.Text.Replace('.', ',')); // Шаг Euler euler = new Euler(); Dictionary // Вывод графиков foreach (var point in show) { for (int i = 0; i < charts.Count; i++) { charts[i].Series[0].Points.AddXY(point.Key, point.Value[i]); } } var y1 = show[T][4]; var forError = euler.getResult(h / 2); var y2 = forError[T][4]; var error = Math.Abs((y2 - y1) / y2) * 100; // Погрешность label3.Text = y1.ToString(); label5.Text = error.ToString(); } private void button2_Click(object sender, EventArgs e) { // Предварительная очистка холстов графиков chart6.Series[0].Points.Clear(); chart7.Series[0].Points.Clear(); Euler euler = new Euler(); for (double h = 0.001; h <= 1; h *= 2) { var y1 = euler.getOnlyResult(h); var y2 = euler.getOnlyResult(h / 2); var error = Math.Abs((y2 - y1) / y2) * 100; // Погрешность chart6.Series[0].Points.AddXY(h, error); chart7.Series[0].Points.AddXY(h, T / h); } } private void button3_Click(object sender, EventArgs e) { // Список объектов графиков var charts = new List // Предварительная очистка холстов графиков foreach (var chart in charts) { chart.Series[0].Points.Clear(); } double h = double.Parse(textBox2.Text.Replace('.', ',')); // Начальный шаг Euler euler = new Euler(); double error; do { var y1 = euler.getOnlyResult(h); var y2 = euler.getOnlyResult(h / 2); error = Math.Abs((y2 - y1) / y2) * 100; h /= 2; } while (error > 1); Dictionary // Вывод графиков int counter = 0; foreach (var point in show) { counter++; if (counter % 50 != 0) // Вывод каждой 50-той точки для ускорения рендеринга графиков { continue; } for (int i = 0; i < charts.Count; i++) { charts[i].Series[0].Points.AddXY(point.Key, point.Value[i]); } } label8.Text = show[T][4].ToString(); label10.Text = error.ToString(); label12.Text = h.ToString(); } } } Выводы В ходе выполнения лабораторной работы была разработана программная имитационная модели нелинейной динамической системы. |
