матем 2-1. Цель закрепление знаний об основных фигурах на плоскости и их свойствах. Задание 1
 Скачать 0.93 Mb. Скачать 0.93 Mb.
|
|
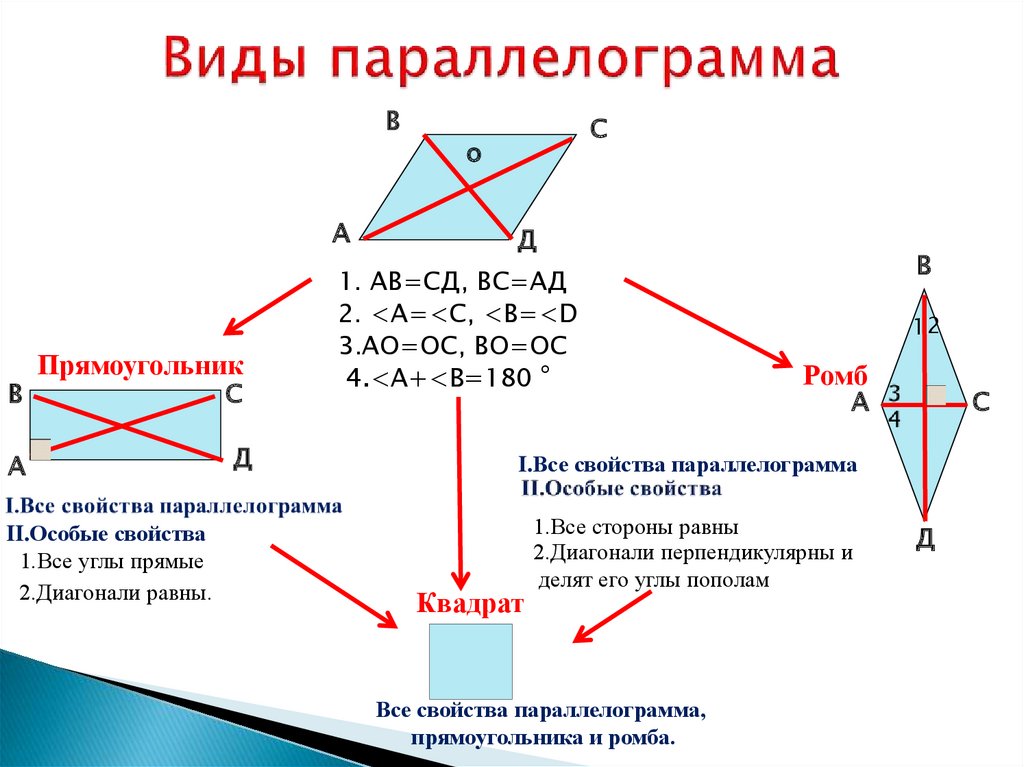
Самостоятельная работа по теме 2.1. Цель: закрепление знаний об основных фигурах на плоскости и их свойствах. Задание 1. 1)Постройте произвольные параллелограмм общего вида, квадрат, прямоугольник, ромб. 2)Укажите основные элементы фигур (диагонали, высоты). 3)Проверьте и напишите свойства каждой построенной фигуры 4) Вычислите площади каждой построенной фигуры, используя различные формулы площадей (через высоту, угол между сторонами, угол между диагоналями) Ответ округлите до сотых. 5) Вычислите периметры каждой построенной фигуры Задание 2 Задание 3 В треугольнике ABC сторона AB=4 см, AС=8 см, а угол A равен 600. Найдите все стороны и все углы треугольника. Задание 4 Меньшее основание равнобедренной трапеции равно 6. Высота трапеции равна 10. Тангенс острого угла равен 2. Найдите большее основание. Задание 5 Докажите, что в равнобедренном треугольнике биссектрисы, проведённые к его боковым сторонам, равны Задание 6. Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении 3:4, считая от вершины тупого угла. Найдите большую сторону параллелограмма, если его периметр равен 88. 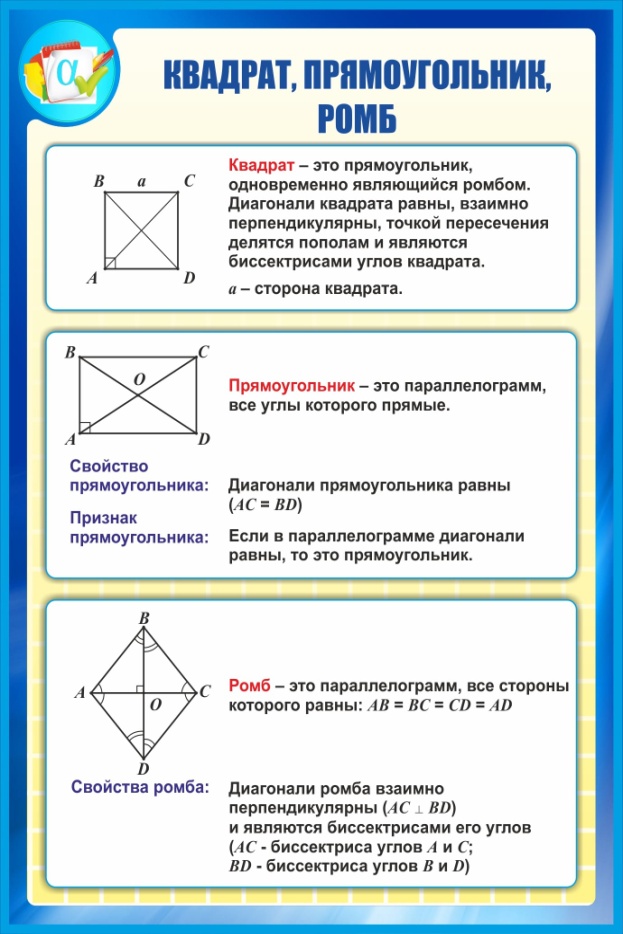 Узнать площадь прямоугольника помогут следующие формулы: Узнать площадь прямоугольника помогут следующие формулы:S = a × b, где a, b — ширина и высота прямоугольника 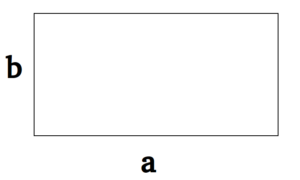 2. S = a × √(d2 - а2), где а — известная сторона, d — диагональ. 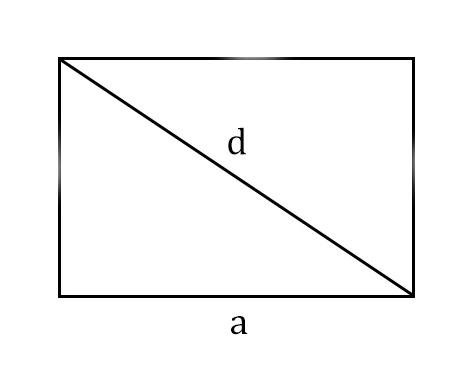 Диагональ — это отрезок, который соединяет противоположные вершины фигуры. Он есть во всех фигурах, число вершин которых больше трех. S = 0,5 × d2 × 𝑠𝑖𝑛(𝑎), где d — диагональ. 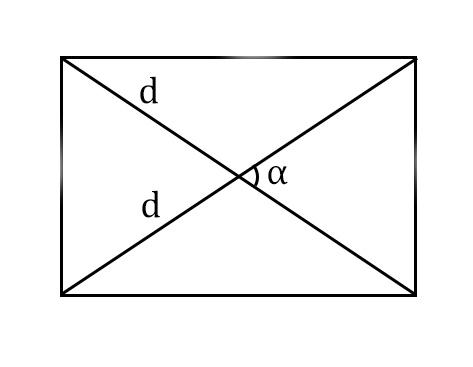 Периметр прямоугольника — сумма длины и ширины, умноженная на два. P = 2 × (a + b), где a — ширина, b — высота. 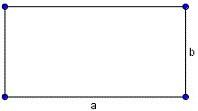 Найти площадь квадрата легко: S = а2, где a — сторона квадрата. 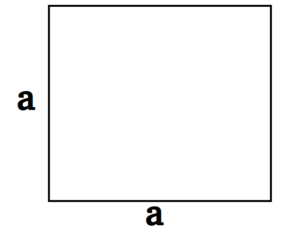 2. S = d2 : 2, где d — диагональ. 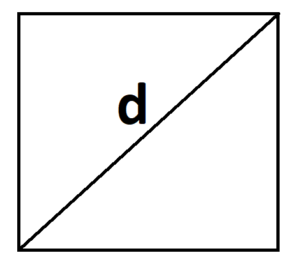 Периметр квадрата — это длина стороны, умноженная на четыре. P = 4 × a, где a — длина стороны.  Общие формулы расчета площади фигур: S = a × h, где a — сторона, h — высота 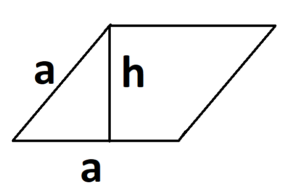 2. S = a × b × sinα, где a и b — две стороны, sinα — синус угла между ними. В случае с ромбом стороны равны, поэтому формула примет вид S = a × a × sinα или S = a2 × sinα. 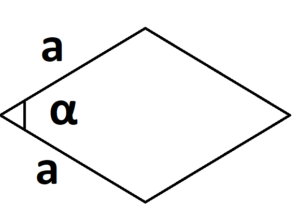 3. Для ромба: S = 0,5 × (d1 × d2), где d1,d2 — две диагонали. Для параллелограмма: S = 0,5 × (d1 × d2) × sinβ, где β — угол между диагоналями. 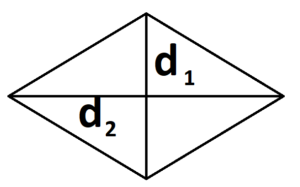 Периметр ромба — это произведение длины стороны на четыре. P = 4 × a, где a — длина стороны.  Периметр параллелограмма — сумма длины и ширины, умноженная на два. P = 2 × (a + b), где a — ширина, b — высота.  4) Вычислите площади каждой построенной фигуры, используя различные формулы площадей (через высоту, угол между сторонами, угол между диагоналями) Ответ округлите до сотых. У нас есть прямоугольник A . Одна его сторона A равна 5 см, вторая B равна 3 см. Нам нужно найти его площадь S  Чтобы найти площадь S, нужно умножить сторону A на сторону B и получаем: S = 5 ⋅ 3 Ответ: S = 15 S = 15S=15 см2. Дан прямоугольник A B C D. Его диагональ A C равна 8 см, а острый угол между диагоналями 30°. Найдите площадь фигуры. Используем приведенную выше формулу и получаем: S = 1/2 ⋅ 8 2 ⋅ sin 30∘ = 1/2 ⋅ 64 ⋅ 1/2 = 64/4 = 16 Ответ: S=16 см2. Расчет Через сторону и высоту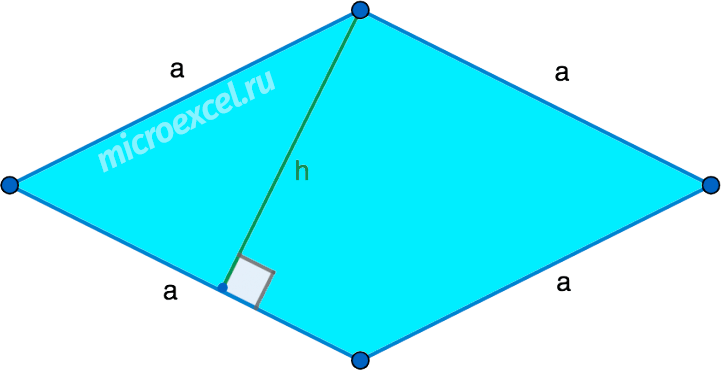 Сторона a: 8 см Высота h:10 см Площадь (S) ромба:80 см Формула расчета S = a ⋅ h 8*10=80 см Через стороны и угол между ними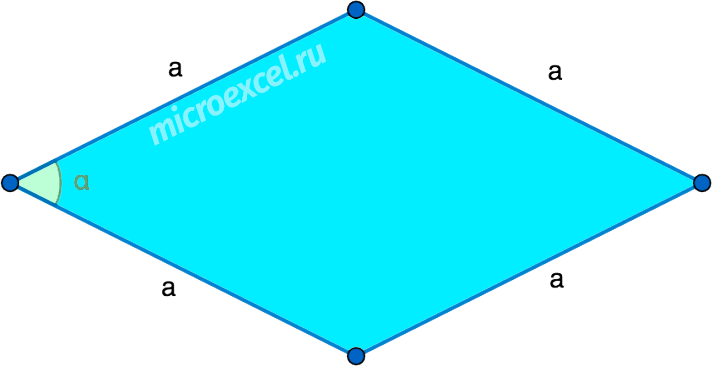 Сторона a: 8 см Угол α в (°): 30° Площадь (S) ромба: 32 см Формула расчета S = a2⋅ sinα 82 * sin30°=32 Через диагонали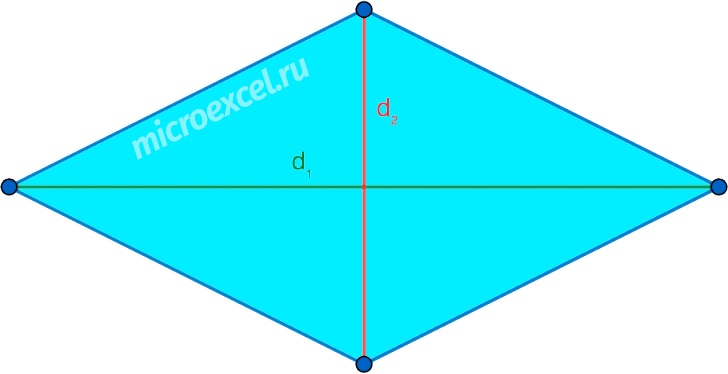 Диагональ d1: 16 см Диагональ d2: 8 см Площадь (S) ромба: 64 см Формула расчета 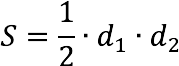 ½ * 16*8=64 5) Вычислите периметры каждой построенной фигуры | ||||||||||||||||||||||||||||||
| Решение | P = 4a = 4 · 4 = 16 |
| | |
| Ответ | P = 16 |
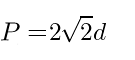
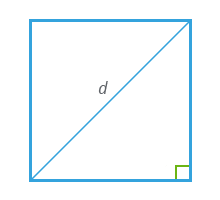
| Решение | P = 2√2d = 2 · √2 · 4 = 11,313708499 |
| | |
| Ответ | P = 11,313708499 |
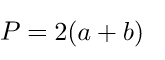

| Решение | P = 2 · (a + b) = 2 · (3 + 5) = 16 |
| | |
| Ответ | P = 16 |
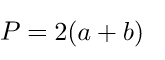
| Решение | P = 2 · (a + b) = 2 · (3 + 8) = 22 |
| | |
| Ответ | P = 22 |
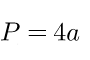
| Решение | P = 4a = 4 · 8 = 32 |
| | |
| Ответ | P = 32 |
Задание 2
Задание 3
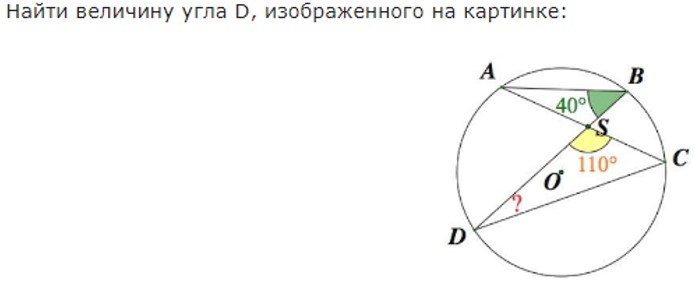
В треугольнике ABC сторона AB=4 см, AС=8 см, а угол A равен 600. Найти все стороны и все углы треугольника.
Угол ASB=DSC = 110 º, как вертикальные
Из треугольника АВС: угол DFS = = 180 º- 110 º - 40 º= 30 º.
Угол ВАС = ВDC = 30 º, так как опираются на одну и ту же дугу
Ответ: 30 º.
Задание 4
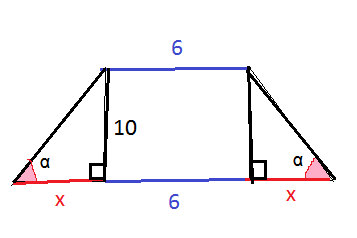
Меньшее основание равнобедренной трапеции равно 6. Высота трапеции равна 10. Тангенс острого угла равен 2. Найдите большее основание.
Проведем высоты из вершин верхнего основания. Получим два равных прямоугольных треугольника и прямоугольник.
tgα=10/x ( отношение противолежащего катета к прилежащему)
По условию
10/х=2
x=10:2=5
a=x+x+b=5+5+6=16
О т в е т. 16
Задание 5
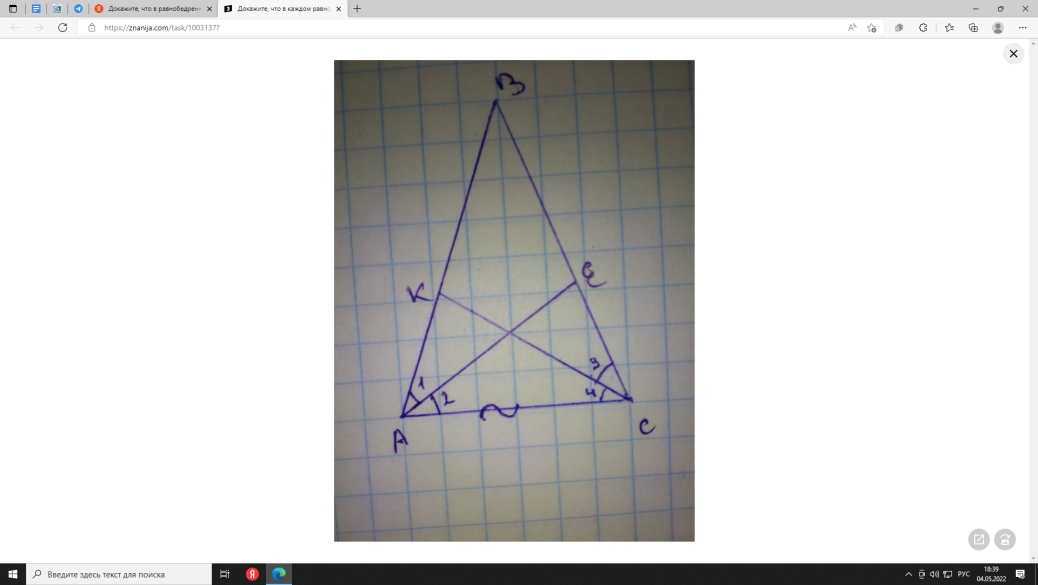
Докажите, что в равнобедренном треугольнике биссектрисы, проведенные к его боковым сторонам, равны
Треугольник АВС - равнобедренный, след-но углы при основании равны, след-во и углы 1, 2, 3, 4 раны(т.к. АЕ и СК - биссектрисы). Треуг.АКС=треуг.АЕС (угл 2=углу 4, угл ВАС = углу ВСА, сторона АС - общая) по стороне и прилежащим к ней углам, след-но КС=АЕ. :)
Задание 6.
Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении 3:4, считая от вершины тупого угла. Найдите большую сторону параллелограмма, если его периметр равен 88.
Пусть BL - данная биссектриса.
∠ABL = ∠LBC - по условию;
∠ALB = ∠LBC - как накрест лежащие;
Значит, ∠ALB = ∠ABL. Тогда ΔABL - равнобедренный ⇒ AB = AL.
Пусть
Тогда
Тогда и
Зная, что P = 88, составим уравнение:
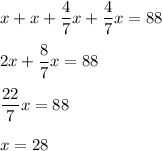
Найденная сторона будет большей.
Ответ: 28.