еонтрольная работа. Методическое пособие по Финансовым вычислениям в MS Excel (ВСЕ).. Частное образовательное учреждение высшего образования

• Название: Частное образовательное учреждение высшего образования
• Анкор: еонтрольная работа
• Дата: 23.11.2021
• Размер: 372.93 Kb.
• Имя файла: Методическое пособие по Финансовым вычислениям в MS Excel (ВСЕ)..docx
• Тип: Документы; #280022
• страница: 2 из 3

Лабораторная работа №2. Оценка инвестиционных процессов

Особенности инвестиционных процессов как объекта финансовой математики

Инвестиции – это долгосрочные финансовые вложения экономических ресурсов с целью создания и получения выгоды в будущем, которая должна быть выше начальной величины вложений.

При анализе потоков платежей используются обобщающие показатели:

• 
  наращенная стоимость;
  
• 
  приведенная стоимость;
  
• 
  норма доходности.
  

Чистый приведенный доход

Поскольку денежные средства распределены во времени, то и здесь фактор времени играет важную роль.

При оценке инвестиционных проектов используется метод расчета чистого приведенного дохода, который предусматривает дисконтирование денежных потоков: все доходы и затраты приводятся к одному моменту времени.

Центральным показателем в рассматриваемом методе является показатель чистого приведенного дохода NPV(net present value) – текущая стоимость денежных потоков за вычетом текущей стоимости денежных оттоков.

Это обобщенный конечный результат инвестиционной деятельности в абсолютном измерении.

При разовой стартовой инвестиции расчет чистого приведенного дохода можно представить следующим выражением:

n

NPV _

^Rk  IC

где

IC– стартовые инвестиции;

i– ставка дисконтирования.

k1 ^{1  i}

R_k– годовые денежные поступления в течение nлет,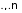

k 1, 2, – моменты времени.
Важным моментом является выбор ставки дисконтирования, которая должна отражать ожидаемый усредненный уровень ссудного процента на финансовом рынке.

Если проект предполагает не разовую инвестицию, а последовательное ^{инвестирование финансовых ресурсов в течение нескольких (} m ^{) лет, то} формула для расчета очевидным образом модифицируется:

n


m
NPV _

R_{k  }





IC<sub>j

j</sub> IC₀

k1 ^{1  i} j1 ^{1  i}
Показатель NPV является абсолютным приростом, поскольку оценивает, на сколько приведенный доход перекрывает приведенные затраты:

• 
  при
  
• 
  при
  
• 
  при
  

NPV 0

NPV 0

NPV 0

проект следует принять (приносит прибыль); проект не принимается (убыточен),

проект не имеет ни прибыли, ни убытков.

Одно из важных свойств данного критерия в том, что показатель NPVразличных проектов можно суммировать, поскольку он аддитивен во времени. Это позволяет использовать его при анализе оптимальности инвестиционного портфеля.

Пример:

Фирма рассматривает целесообразность инвестиционного проекта, стоимость которого составляет 210 тыс. долларов.

По прогнозам ежегодные поступления составят 55 тыс. долларов. Проект рассчитан на 5 лет.

Необходимая норма прибыли составляет 8%. Следует ли принять этот проект?

Решение:

Чистая стоимость проекта (чистый приведенный доход) равна:

n

NPV _

^k _k IC₀ 

R
k1 ^{1  i}

_ 55000 _ 55000 _ 55000 _ 55000 _ 55000 _{ 210000  5735}



1,08¹ 1,08² 1,08³ 1,08⁴ 1,08⁵

Поскольку величина чистой текущей стоимости проекта оказалась равна

–5735 долларов, т.е.

NPV 0 , то проект должен быть отвергнут.

Как правило, основываются на том, что величина NPVнаходится на начало реализации инвестиционного проекта (чистая текущая стоимость проекта). Однако можно определять эту величину на момент завершения процесса вложений или на иной момент времени.

Несмотря на изменение абсолютного результата, знак данной величины не меняется от изменения момента приведения. Следовательно, вывод о принятии проекта не зависит от момента приведения.

Часто возникают ситуации оценки инвестиционного проекта, который, начиная с некоторого момента времени n₀ , будет приносить постоянный доход

R_k R

или доход с постоянным темпом роста h: R_k

^{ R}^{1  h}^k

(инвестиции в

предприятия, торговлю и т.п.). В этом случае имеет место инвестиционный проект с бесконечным периодом получения доходов. Обобщая формулу для чистого приведенного дохода на бесконечное количество моментов времени, получим:


^ R _1  h_^{k m}

IC_j

NPV

 _

kn₀

^{1  i}^k



j1 ^{1  i} ^j

• 
  IC₀
  

Если ставка дисконтирования больше, чем темп роста дохода ( i h), то бесконечную сумму можно выразить по формуле для бесконечной геометрической прогрессии с убывающими членами:

j1
_ 1  h_ⁿ⁰

_1  i_ ^{m IC}_j

 
NPV

 R _{ 1  i}

^ _i h_ ^{ }_{1  i} ^j

• 
  IC₀
  

Для постоянного дохода Rформулы справедливы при

Пример:

h  0 .

Инвестор рассматривает целесообразность вложения 150 млн. руб. в покупку магазина, который приносит доход 10 млн. руб. в год и этот доход растет наравне с инфляцией с темпом роста 8% в год. Необходимая норма прибыли инвестора составляет 15%.

Следует ли принять этот проект?

Решение:

Заметим, что в этом случае период начала поступления дохода n₀  1, а

инвестиции вкладываются лишь однократно и равны сумме покупки.

Так как i 0,15  h 0,08, то можно воспользоваться формулой для


 
чистого приведенного дохода на бесконечном количестве периодов.

_ 1 h_ⁿ⁰

^{1 i}

 ^{1 0, 08} ¹

^{1 0,15}

NPV

 R_{ 1 i}

^ ^{i h} ^{ IC0  10  1 0,15 }

 150  4, 29

0,15  0, 08

млн.р.

^{ }  

Чистый приведенный доход от объекта вложения положителен, следовательно проект рекомендуется принять.

Если ожидаемый темп роста доходов не ниже ставки дисконтирования ( i  h ), то такой проект, очевидно, является выгодным, а чистый приведенный доход по нему равен бесконечности.

Срок окупаемости

Для анализа инвестиций применяют и такой показатель, как срок (период) окупаемости (payback period method) – продолжительность времени, в течение которого дисконтированные на момент завершения инвестиций прогнозируемые денежные поступления равны сумме инвестиций. В этом

случае, очевидно,

NPV 0

и получаем:

^tок