 Частное образовательное учреждение высшего образования Частное образовательное учреждение высшего образования «Казанский инновационный университет имени В. Г. Тимирясова (ИЭУП)» Кафедра высшей математики З.Ш. Аглямова, Д.Т. Суючева, Е.А. Храмкова, Д.В. ШевченкоМетодическое пособиепо финансовым вычислениям в MS Excel Оглавление
Введение 3
Лабораторная работа №1. Использование финансовых функций в
финансовых операциях. Операции наращения и дисконтирования в EXCEL . 4 Лабораторная работа №2. Оценка инвестиционных процессов 14
Введение
Использование пакетов прикладных программ для финансовых расчетов является неотъемлемой частью изучения дисциплины «Финансовая математика». В результате обучения студенты должны уметь обрабатывать данные финансовых вычислений с помощью финансовых функций EXCEL, использующих базовые модели финансовых операций, опирающиеся на математический аппарат методов финансово-экономических расчетов.
Финансовые функции EXCEL предназначены для проведения финансово-коммерческих расчетов по кредитам и займам, финансово- инвестиционного анализа, ценным бумагам.
При работе с финансовыми функциями необходимо учитывать специфику задания значения аргументов:
все расходы денежных средств (платежи) представляются отрицательными числами, а все поступления денежных средств – положительными числами;
процентная ставка вводится с использованием знака %;
все даты как аргументы функций имеют числовой формат.
Весь учебный материал разделен на 2 занятия. Каждое занятие содержит разобранные задания и задания для самостоятельного решения, которые позволят студенту наиболее полно и глубоко изучить материал.
Лабораторная работа №1. Использование финансовых функций в финансовых операциях. Операции наращения и
дисконтирования в EXCEL
Операции наращения
Функции, обслуживающие расчеты по операциям наращения позволяют рассчитать будущую стоимость разовой суммы по простым и сложным процентам, а также будущее значение потока платежей, как на основе постоянной процентной ставки, так и на основе переменной процентной ставки.
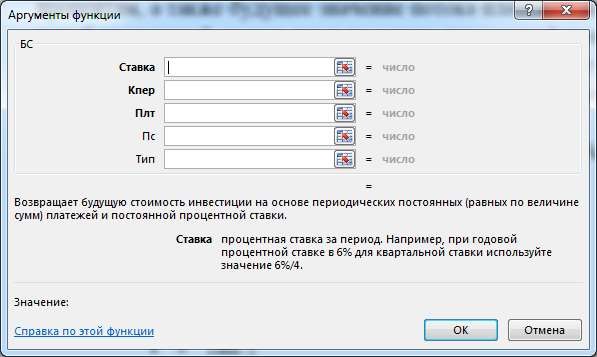 Функция БС – будущая стоимость – рассчитывает наращенную величину разовой денежной суммы и/или периодических постоянных платежей на основе постоянной процентной ставки. Функция БС – будущая стоимость – рассчитывает наращенную величину разовой денежной суммы и/или периодических постоянных платежей на основе постоянной процентной ставки.
С ее помощью можно упростить расчет FV или FVA. Аргументы данной функции:
ставка;
число периодов;
периодическая выплата;
приведенная (или нынешняя) стоимость;
тип.
Для правильного ввода аргументов необходимо идентифицировать их с классическими обозначениями:
ставка – процентная ставка (i);
число периодов – срок финансовой операции или общее число раз начисления процентов за весь срок финансовой операции (n или m • n);
периодическая выплата – член финансовой ренты (R);
приведенная стоимость – начальное значение, т.е. первоначальная сума долга (PV);
тип – вид финансовой ренты в зависимости от метода выплаты платежей: платежи в конце периода, т.е. обычная рента или пренумерандо – число 1, платежи в начале периода, т.е. постнумерандо
Для решения задач наращения без исследования периодических потоков платежей следует помнить, что не все аргументы рассматриваемой функции используются в этом случае.
Рабочими аргументами являются:
Остальные аргументы не используются.
Пример:
Определить наращенную сумму для вклада в размере 5000 руб., размещенного под 12% годовых на один год.
Решение:
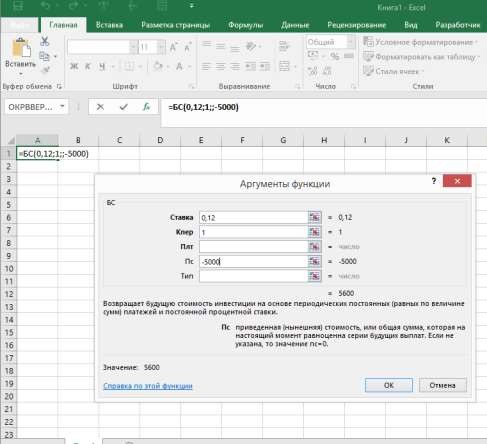
В верхней части диалогового окна Ввода аргументов функции в ячейке "Значение" появится ответ: 5600,00.
Таким образом, через год наращенная сумма составит 5'600,00 руб.
лет.
Обратите внимание, что в аргументах годовой процент и целое число
Если продолжительность финансовой операции представлена в днях, то
необходимо ввести корректировку в процентную ставку, т.е. аргумент норма будет представлен как t / T • i%. Пример: Вклад размером в 2000 руб. положен с 06.06 по 17.09 невисокосного года под 30% годовых. Найти величину капитала на 17.09 по различной практике начисления процентов. Решение: Германская практика начисления процентов: 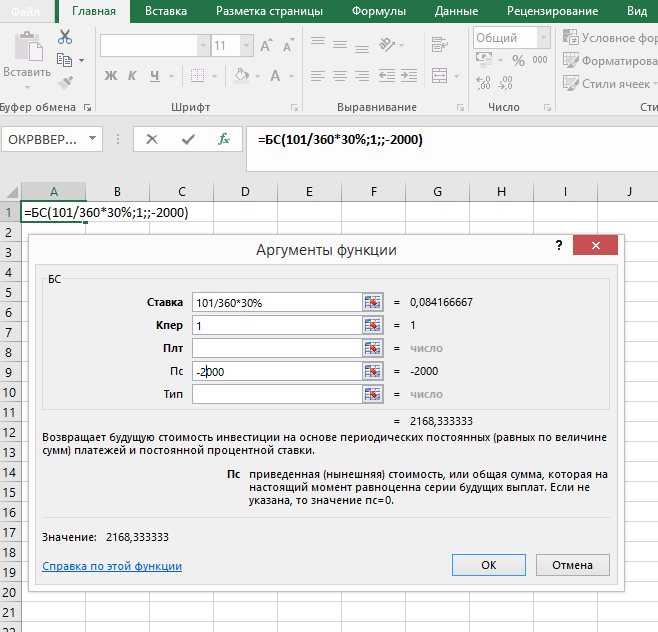
Английская практика начисления процентов:
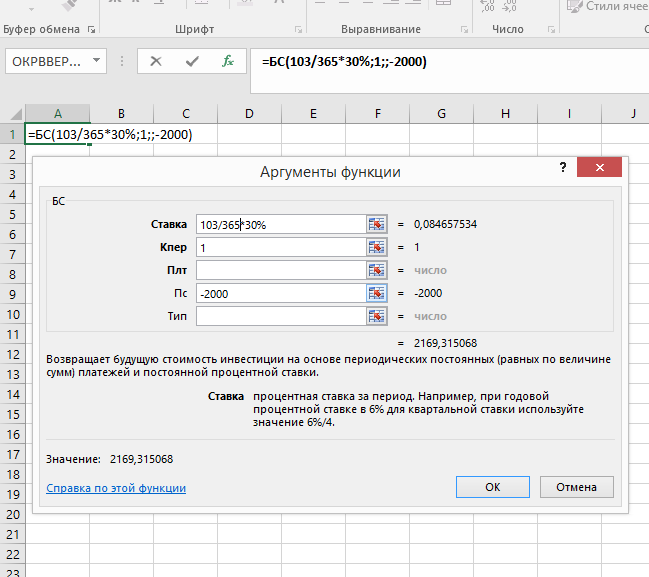
Значение 2169,32.
Французская практика начисления процентов:

Таким образом, начисление процентов по германской практике приведет к получению суммы в размере 2168,33 руб., по английской практике – 2169,32 руб., по французской практике – 2171,67 руб.
Сложныепроценты.
При использовании сложных процентов используются те же аргументы, что и в простых процентах, с использованием годовой процентной ставки и целого числа лет.
Пример:
Какая сумма будет на счете через три года, если 5000 руб. размещены под 12% годовых.
Решение:
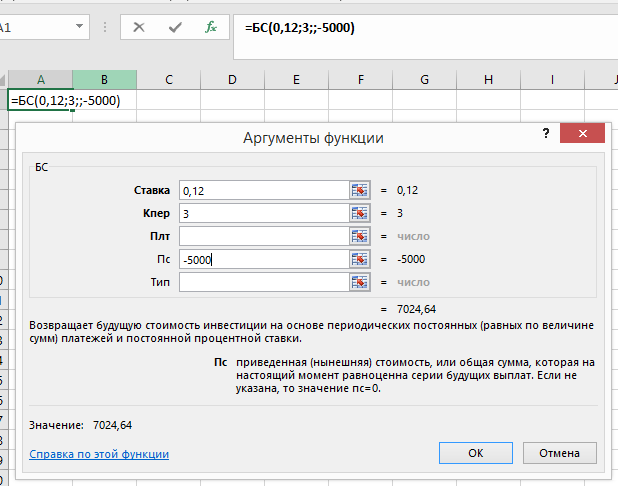
Значение 7024,64.
Таким образом, через три года на счете будет 7'024,64 руб.
Если же период начисления процентов будет меньше года, то необходимо модифицировать аргументы норма и число периодов:
норма – берется ставка процентов за период начисления, т.е. используется номинальная годовая ставка процентов, скорректированная на число раз начисления процентов в течение года j% / m;
число периодов – указывается общее число раз начисления процентов за весь срок финансовой операции n • m.
Пример:
Используем условия предыдущего примера, но проценты будут начисляться каждые полгода.
Решение:
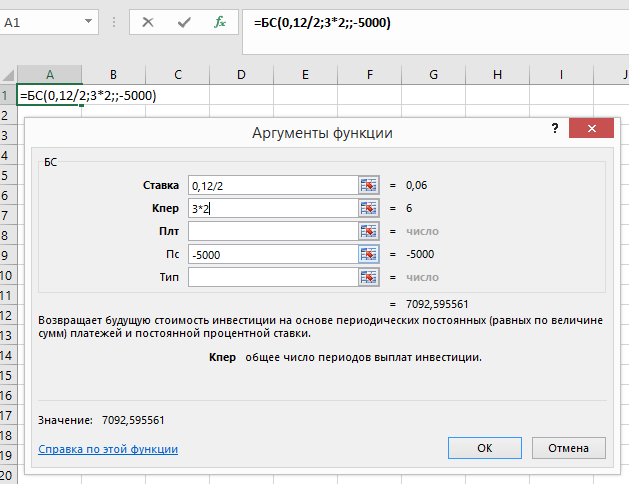
Значение 7092,60.
Следовательно, при полугодовом начислении процентов на счете будет 7'092,60 руб.
Операции дисконтирования
Для многих финансовых операций необходимо использовать данные о приведенных или современных денежных величинах, как разовой суммы, так и потоков фиксированных периодических платежей.
Для облегчения расчетов используется функция ПС – первоначальная стоимость (PV).
Аргументы функции:
ставка;
Кпер;
Плт;
БС;
тип.
Этот расчет является обратным к определению наращенной суммы при помощи функции БЗ, поэтому сущность используемых аргументов в этих функциях аналогична.
Вместе с тем, вводится новый аргумент БС – будущая стоимость или будущее значение денежной суммы (FV), а также иное обозначение числа периодов – кпер – (n или n • m).
Рассматриваемая функция может быть использована для расчета по простым и сложным процентам.
Пример:
Через 125 дней следует накопить сумму в размере 2,5 тыс. руб. Какой должен быть размер вклада, размещаемый под 5%?
Решение:
Определяем первоначальную сумму долга:
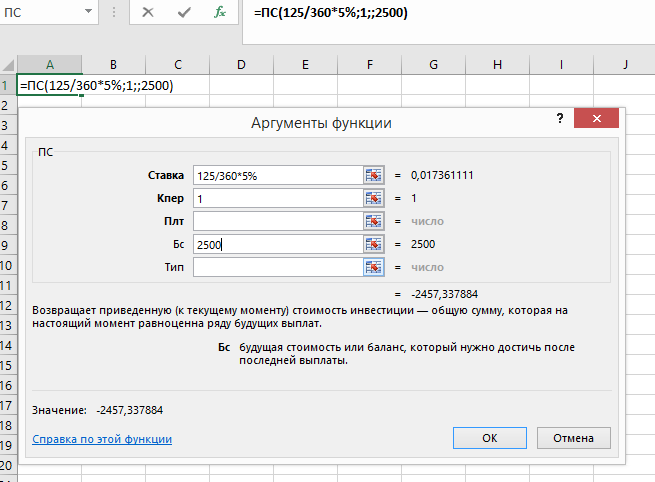
*Положительное значение означает поступление денег. Значение -2457,34
На указанных условиях следует положить 2'457,34 руб., что позволит через 125 дней получить 2'500 ,00 руб.
Текущее значение единой суммы вклада с использованием сложных процентов и неоднократным начислением процентов в течение года рассчитывается аналогично.
Пример:
Требуется получить на лицевом счете 50 тыс. руб. через три года. Выбрать варианты размещения средств:
под 26% с полугодовым начислением процентов;
под 24% годовых с ежеквартальным начислением процентов.
Решение:
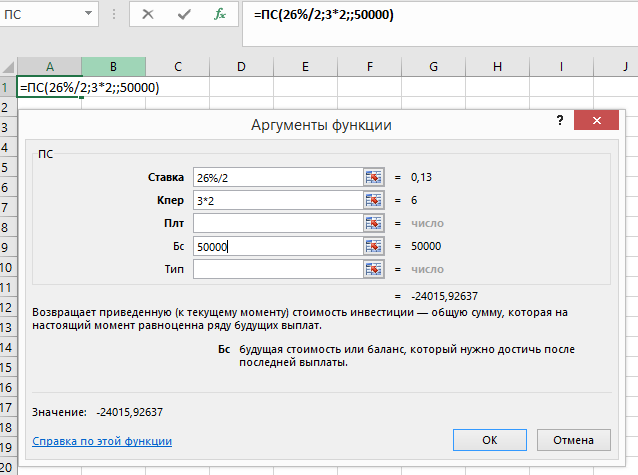 Используем функцию ПЗ. Для первого варианта: Используем функцию ПЗ. Для первого варианта:
Значение -24015,93. Для второго варианта:
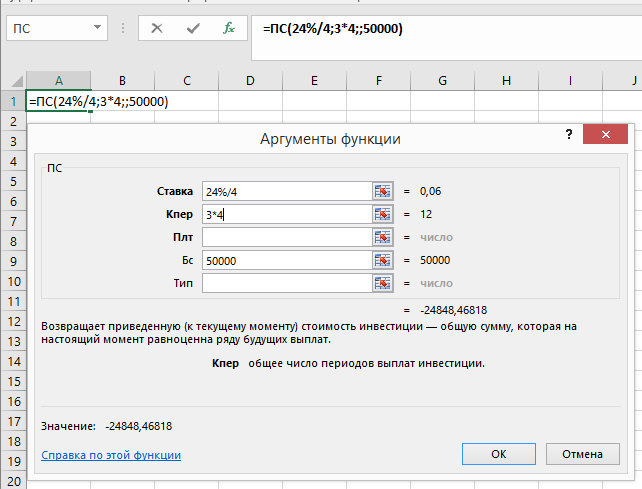
Значение -24848,47.
Таким образом, предпочтителен первый вариант, поскольку имеет меньшую первоначальную величину.
Задачи для самостоятельного решения
Применяя финансовые функции EXCEL выполните следующие задания:
Задача 1
Ссуда, размером 150 000 руб., выдана на срок с 21 января 2019 г. до 3 марта 2019 г. при ставке простых процентов, равной 25% годовых. Найти сумму начисленных процентов по германской, французской и британской практике.
Задача 2
В кредитном договоре на сумму 1 000 000 руб. и сроком на 4 года зафиксирована ставка сложных процентов, равная 20% годовых. Определить наращенную сумму.
Задача 3
Ссуда 20 млн руб. предоставлена на 28 месяцев. Проценты сложные, ставка 18% годовых. Проценты начисляются ежеквартально. Вычислить наращенную сумму по истечении срока.
Задача 4
Через 90 дней после подписания договора должник уплатит 1 млн.руб. Кредит выдан под 15% годовых (проценты обыкновенные). Рассчитать первоначальную сумму и дисконт.
Задача 5
Через 5 лет предприятию будет выплачена сумма 650 тыс.руб. Определить его современную стоимость при условии, что применяется ставка сложных процентов в 14% годовых.
|
 Скачать 372.93 Kb.
Скачать 372.93 Kb.