МХТП контрольная 1. Чернева А. В., Охт16. 01
 Скачать 69.91 Kb. Скачать 69.91 Kb.
|
|
Чернева А.В., ОХТ-16.01 2. Для теплообменника, указанного в задаче 1, принять: движение потока в трубном пространстве характеризуется моделью идеального вытеснения, в межтрубном – однопараметрической диффузионной моделью. Построить модель с учетом тепловой инерционности стенок трубного пространства. Потерями в окружающую среду пренебречь.                δ δ  TХ  qХ D TХ+ΔT qХ D TХ+ΔT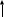 VХ VХ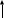             ΔX qТ ΔX qТ X D - внутренний диаметр трубы; qx, qт – тепловые потоки; Tх – температура хладагента; Vх – объем хладагента; δ – толщина стенки. Математическую модель строим для одиночной трубы, принимая, что в каждой трубе процесс протекает одинаково. Запишем уравнение закона сохранения тепла в общем виде: 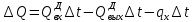 (1) (1)где 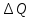 – накопление тепла в выделяемом элементарном объеме [Дж]; – накопление тепла в выделяемом элементарном объеме [Дж]; 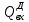 , , 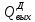 – тепловые потоки, характеризующие продольное перемешивание на входе и выходе элементарного объема [Вт]; – тепловые потоки, характеризующие продольное перемешивание на входе и выходе элементарного объема [Вт]; 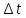 – элементарный промежуток времени [с]. – элементарный промежуток времени [с].Определим отдельные слагаемые этого уравнения: 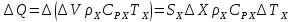 (2) (2)где 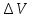 – элементарный объем теплообменного пространства; – элементарный объем теплообменного пространства; 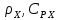 – плотность и теплоемкость хладагента; – плотность и теплоемкость хладагента; 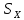 – сечение, в котором движется хладагент. – сечение, в котором движется хладагент.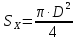 (3) (3)Для определения 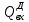 и и 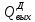 используем первый закон Фика (распределение температуры совпадает с распределением массы) в виде: используем первый закон Фика (распределение температуры совпадает с распределением массы) в виде: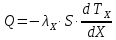 (4) (4)где 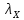 – коэффициент продольного перемешивания по температуре. – коэффициент продольного перемешивания по температуре.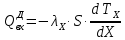 (5) (5)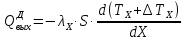 (6) (6)Используя закон теплоотдачи Ньютона, определим 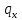 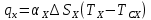 (7) (7)где 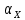 – коэффициент теплоотдачи со стороны хладагента. – коэффициент теплоотдачи со стороны хладагента.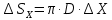 (8) (8)Таким образом, получим следующее уравнение теплового баланса: 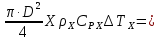 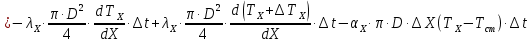 (9) (9)Разделим это уравнение на 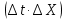 и перейдем к пределу при и перейдем к пределу при 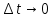 , , 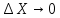 . Учитывая, что . Учитывая, что 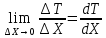 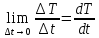 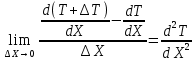 Получим: 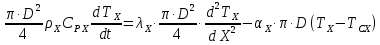 (10) (10)Составим уравнение теплового баланса для хладагента. Уравнение составляем для всего объема жидкости. Это уравнение имеет вид: 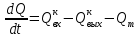 (11) (11)где 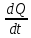 – скорость накопления тепла в объеме жидкости; – скорость накопления тепла в объеме жидкости; 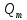 – полное количество тепла, принимаемое всей поверхностью трубы к жидкости в единицу времени. – полное количество тепла, принимаемое всей поверхностью трубы к жидкости в единицу времени.Используя закон теплопередачи, определим 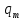 как как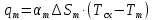 (12) (12)где 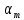 – коэффициент теплоотдачи со стороны теплоносителя; – коэффициент теплоотдачи со стороны теплоносителя; 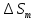 – элемент поверхности теплоотдачи со стороны теплоносителя. – элемент поверхности теплоотдачи со стороны теплоносителя.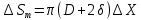 (13) (13)По определению 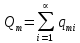 , поэтому , поэтому 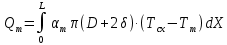 (14) (14)где 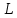 – длина труб. – длина труб.В соответствии с допущениями 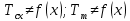 , следовательно , следовательно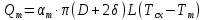 (15) (15)Определим остальные слагаемые уравнения теплового баланса 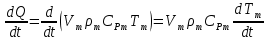 (16) (16)где 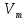 – объем жидкости. – объем жидкости.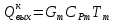 (17) (17)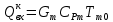 (18) (18)окончательно получим: 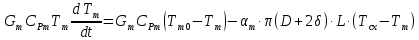 (19) (19)В уравнениях 17, 19 3 неизвестных величины: 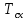 , , 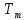 , , 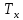 – поэтому составляем третье уравнение – тепловой баланс стенки. Уравнение составляем для элементарного объема стенки – поэтому составляем третье уравнение – тепловой баланс стенки. Уравнение составляем для элементарного объема стенки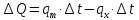 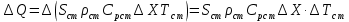 (20) (20)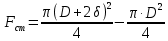 (21) (21)где 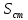 – сечение стенки, – сечение стенки, 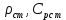 – плотность и теплоемкость материала стенки. Комбинируя уравнения 7, 12, 21, выполнив соответствующие сокращения, разделив на – плотность и теплоемкость материала стенки. Комбинируя уравнения 7, 12, 21, выполнив соответствующие сокращения, разделив на 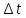 и переходя к пределу и переходя к пределу 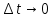 , получим: , получим: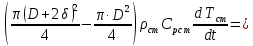 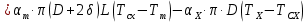 (22) (22)по условию задачи необходимо построить модель с учетом тепловой инерционности стенки, поэтому 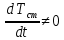 . Таким образом, построена математическая модель заданного процесса, представляющая собой следующую систему дифференциальных уравнений: . Таким образом, построена математическая модель заданного процесса, представляющая собой следующую систему дифференциальных уравнений: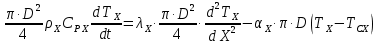 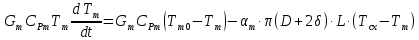 (22) (22)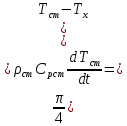 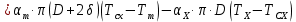 Трубное пространство представлено моделью идеального вытеснения, межтрубное – однопараметрической диффузионной моделью. Для синтеза системы автоматического управления удобнее представить математическую модель проточного бака в виде системы передаточных функций. Передаточные функции можно получить только из дифференциальных уравнений в обычных производных, поэтому модель идеального смешения для трубного пространства, которая описывается дифференциальным уравнением в частных производных, необходимо заменить на ячеечную модель. Ячеечная модель описывается системой дифференциальных уравнений в обычных производных. При правильном выборе количества ячеек замена диффузионной модели гидродинамики потока на ячеечную не приводит к потере адекватности модели объекта. При решении задачи рекомендуется разбивать объект на три ячейки. Схематическое изображение трубы показано на рис. 1.  Рис. 1. - Схематическое изображение трубы в виде ячеек. Дифференциальные уравнения, описывающие ячеечную модель трубного пространства, можно получить непосредственно из уравнения 10. Членом, учитывающим идеальное вытеснения, можно пренебречь, т.к. для каждой ячейки принимается модель идеального перемешивания, и производная 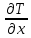 заменяется на разностное выражение заменяется на разностное выражение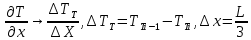 (23) (23)где 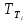 – температура на выходе i-той ячейки; L – длина трубы в аппарате. – температура на выходе i-той ячейки; L – длина трубы в аппарате.Для первой ячейки: 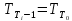 . .Система уравнений, описывающая ячеечную модель, будет иметь: 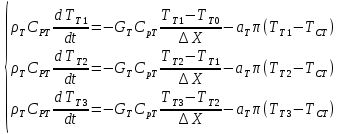 (24) (24)Изменится уравнение, описывающее стенку (третье уравнение системы 22). 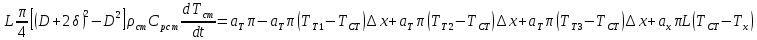 (25) (25) Общая система уравнений, описывающая теплообменный процесс в баке, будет состоять из уравнений 24, 25 второго уравнения системы 22. Из каждого дифференциального уравнения математической модели можно получить несколько передаточных функций. Рассмотрим методику получения передаточных функций на примере первого уравнения: 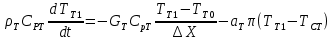 (26) (26)Выходной переменной в этом уравнении является 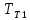 . .Входными параметрами будут: 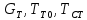 , то есть переменные, изменение которых приводит к изменению выходной переменной. Следовательно, из рассматриваемого уравнения можно получить три передаточные функции: , то есть переменные, изменение которых приводит к изменению выходной переменной. Следовательно, из рассматриваемого уравнения можно получить три передаточные функции: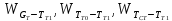 . .Для нахождения линейной передаточной функции 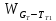 по каналу по каналу 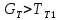 , из нелипейного уравнения 26 необходимо дать приращения по переменным канала, то есть уравнения 26 вместо , из нелипейного уравнения 26 необходимо дать приращения по переменным канала, то есть уравнения 26 вместо 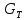 и и 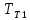 подставить выражения: подставить выражения: 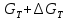 и и 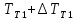 соответственно. соответственно.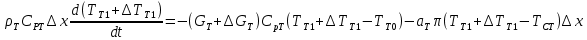 , (27) , (27)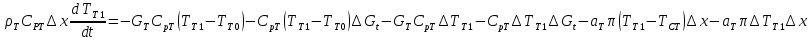 . (28) . (28)Для получения уравнения в приращениях необходимо вычесть из уравнения 28 уравнение 26, получим: 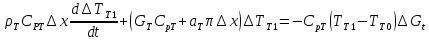 . (29) . (29)Членом - 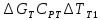 – можно пренебречь, т.к. это величина второй степени малости (произведение двух малых величин - – можно пренебречь, т.к. это величина второй степени малости (произведение двух малых величин - 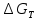 и и 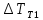 ), тогда: ), тогда: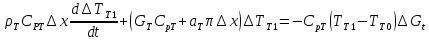 (30) (30)После преобразования по Лапласу уравнение 26, передаточная функция примет вид: 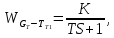 где 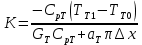 ; ;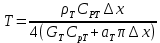 Аналогичным образом необходимо получить все передаточные функции: Из первого уравнения 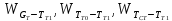 Из второго уравнения 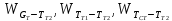 Из третьего уравнения 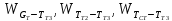 Из четвертого уравнения 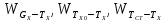 Из пятого уравнения 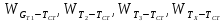 |
