Ответы на вопросы. Численные методы Найти абсолютную погрешность равенства 0,33

• Название: Численные методы Найти абсолютную погрешность равенства 0,33
• Анкор: Ответы на вопросы
• Дата: 10.02.2022
• Размер: 235.62 Kb.
• Имя файла: Chislen_Metody.docx
• Тип: Документы; #356905
• страница: 5 из 9

Решаем уравнение f(x) = 0 методом касательных. Какое значение x принимаем за подвижный конец?

Правильный ответ:
x = b

457. 
     
     Решаем уравнение f(x) = 0 методом половинного деления. Какое значение x принимаем за нулевое приближение?
     

Правильный ответ:
x =

458. 
     Решаем уравнение f(x) = 0 методом итераций, представив в виде
     
     x = (x). Какое значение x принимаем за нулевое приближение?
     

Правильный ответ:
x – любое число из промежутка (a; b)

459. 
     Процесс нахождения приближенных значений корней уравнения разбивается на …
     

Правильный ответ:
отделение корней и уточнение корней до заданной степени точности

460. 
     Количество действительных положительных корней алгебраического уравнения Pn(x) = 0 с действительными коэффициентами (подсчитываемыми каждый столько раз, какова его кратность) либо равно числу перемен знака в последовательности коэффициентов уравнения, либо на четное число меньше.
     Это правило …
     

Правильный ответ:
Декарта

461. 
     Верхняя граница положительных корней уравнения Pn(x) = 0 по методу Лагранжа находится по формуле …
     

Правильный ответ:
, m – номер первого отрицательного коэффициента, B – наибольшая из абсолютных величин отрицательных коэффициентов Pn(x)

462. 
     К способам уточнения корней не относится …
     

Правильный ответ:
метод проб, метод хорд, метод касательных, метод итераций

463. 
     Число отрицательных корней уравнения Pn(x) = 0 равно числу …
     

Правильный ответ:
перемен знака в последовательности коэффициентов Pn(-x) или на четное число меньше

464. 
     Верхняя граница положительных корней уравнения Pn(x) = 0 по методу Ньютона находится по формуле …
     

Правильный ответ:
, при котором Pn(x) и все производные принимают положительные значения

465. 
     Идея метода хорд состоит в том, что на достаточно малом промежутке [a, b] дуга кривой y = f(x) заменяется стягивающей ее хордой. В качестве приближенного значения корня принимается точка пересечения хорды с осью Ox. Координаты этой точки определяются формулой …
     

Правильный ответ:

466. 
     Если уравнение полное, то …
     

Правильный ответ:
количество его положительных корней равно числу перемен знака в последовательности коэффициентов или на четное число меньше, а количество отрицательных корней – числу постоянств знака или на четное число меньше

467. 
     Верхняя граница положительных корней уравнения Pn(x) = 0 по правилу кольца находится по формуле …
     

Правильный ответ:

468. 
     Если для получения значения функции по данному значению аргумента нужно выполнить арифметические операции и возведение в степень с рациональным показателем, то функция называется …
     

Правильный ответ:
алгебраической

469. 
     Идея метода касательных состоит в том, что на достаточно малом промежутке [a, b] дуга кривой y = f(x) заменяется касательной к этой кривой. В качестве приближенного значения корня принимается точка пересечения хорды с осью Ox. Координаты этой точки определяются формулой …
     

Правильный ответ:

470. 
     Число действительных корней уравнения 5x3 - 20x + 3 = 0 по правилу Штурма равно …
     

Правильный ответ:
два положительных корня, один отрицательный корень

471. 
     Если для получения значения функции по данному значению аргумента нужно выполнить арифметические операции и возведение в степень с целым показателем, то функция называется …
     

Правильный ответ:
рациональной

472. 
     Идея метода итерации состоит в том, что уравнение (x) = 0 заменяется равносильным ему уравнением x = f(x). В качестве приближенного значения корня принимается значение, которое определяется формулой …
     

Правильный ответ:

473. 
     Отделение корней уравнения 5x3 - 20x + 3 = 0 по правилу Штурма в интервалах до длины, равной 1, показало, что корни расположены в интервалах …
     

Правильный ответ:
(-3; -2); (0; 1); (1; 2)

474. 
     Дано уравнение 2x3 - 5x2 + 4x - 3 = 0. Для того, чтобы отделить корни графически …
     

Правильный ответ:
строим графики y = 2x3 и y = 5x2 - 4x + 3

475. 
     Корень уравнения 2x3 - 5x2 + 4x - 3 = 0 отделен на промежутке (1; 2). По методу хорд, за неподвижный конец промежутка принимаем:
     

Правильный ответ:
x = 2

476. 
     Корень уравнения f(x) = 0 отделен на промежутке (-2; -1). По методу половинного деления за нулевое приближение принимаем x =:
     

Правильный ответ:

477. 
     Отделить корень уравнения lgx = 1 – x2.
     

Правильный ответ:
x (0;1)

478. 
     Корень уравнения 2x3 - 5x2 + 4x - 3 = 0 отделен на промежутке (1; 2). По методу половинного деления за нулевое приближение принимаем:
     

Правильный ответ:
x = 1,5

479. 
     Корень уравнения f(x) = 0 отделен на промежутке (-2; -1). Пусть
     f '(x) < 0 f(-2) < 0 на (-2; -1). По методу хорд за нулевое приближение принимаем x =:
     

Правильный ответ:

480. 
     Отделить корень уравнения sinx = x - 2.
     

Правильный ответ:
x (1;3)

481. 
     Дано уравнение 2x3 - 5x2 + 4x - 3 = 0. Если корень отделен, то для того, чтобы решить уравнение методом итераций, …
     

Правильный ответ:
записываем уравнение в виде x = (x), …

482. 
     Корень уравнения 2x3 - 5x2 + 4x - 3 = 0 отделен на промежутке
     (1; 2). По методу хорд, за неподвижный конец принимаем:
     

Правильный ответ:
x = 2

483. 
     Корень уравнения f(x) = 0 отделен на промежутке (-2; -1). Пусть
     f ''(x) < 0 f(-2) < 0 на (a; b). По методу касательных за нулевое приближение принимаем x =:
     

Правильный ответ:

484. 
     Отделить корень уравнения cosx + x = 0.
     

Правильный ответ:
x (-1;0)

485. 
     Дано уравнение 2x3 - 5x2 + 4x - 3 = 0. Если корень отделен, то для того, чтобы решить уравнение методом хорд …
     

Правильный ответ:
находим вторую производную, определяем ее знак, …

486. 
     Корень уравнения 2x3 - 5x2 + 4x - 3 = 0 отделен на промежутке
     (1; 2). По методу касательных, за подвижный конец принимаем:
     

Правильный ответ:
x = 1

487. 
     Отделить корень уравнения = 5 - x.
     

Правильный ответ:
x (3;4)

488. 
     Используя метод Эйлера, найти значения функции y, определяемой дифференциальным уравнением y' = xy + 2 при начальном условии y(0) = 1; шаг h = 0,1. Найти только y1:
     

Правильный ответ:
1,2

489. 
     Используя метод Эйлера, найти значения функции y, определяемой дифференциальным уравнением y'' = y' + xy + 1 при начальных условиях y(0) = 1; y'(0) = 0 шаг h = 0,1. Найти только y1:
     

Правильный ответ:
0,1

490. 
     Используя метод Эйлера, найти значения функции y, определяемой дифференциальным уравнением y''' = xy' + 1 при начальных условиях y(1) = 1; y'(1) = 0; y''(1) = 1 шаг h = 0,1. Найти только y1:
     

Правильный ответ:
1,1

491. 
     Используя метод Эйлера, найти значения функции y, определяемой дифференциальным уравнением y' = x2 - y при начальном условии y(0) = 1; шаг h = 0,1. Найти только y1:
     

Правильный ответ:
0,9

492. 
     Используя метод Эйлера, найти значения функции y, определяемой дифференциальным уравнением y'' = yy' + x при начальных условиях y(0) = 1; y'(0) = 0 шаг h = 0,1. Найти только y1:
     

Правильный ответ:
0

493. 
     Используя метод Эйлера, найти значения функции y, определяемой дифференциальным уравнением y''' = xy'' + y' при начальных условиях y(1) = 1; y'(1) = 0; y''(1) = 1 шаг h = 0,1. Найти только y1:
     

Правильный ответ:
1,1

494. 
     Используя метод Эйлера, найти значения функции y, определяемой дифференциальным уравнением y' = 5x + y + 3 при начальном условии y(0) = 1; шаг h = 0,1. Найти только y1:
     

Правильный ответ:
1,4

495. 
     Используя метод Эйлера, найти значения функции y, определяемой дифференциальным уравнением y'' = y' + y + 1 при начальных условиях y(0) = 1; y'(0) = 0 шаг h = 0,1. Найти только y1:
     

Правильный ответ:
0,2

496. 
     Используя метод Эйлера, найти значения функции y, определяемой дифференциальным уравнением y''' = x2y'' + 2 при начальных условиях y(1) = 1; y'(1) = 0; y''(1) = 1 шаг h = 0,1. Найти только y1:
     

Правильный ответ:
1,3

497. 
     Используя метод Эйлера, найти значения функции y, определяемой дифференциальным уравнением y' = y2 - x при начальном условии y(0) = 1; шаг h = 0,1. Найти только y1:
     

Правильный ответ:
1,1

498. 
     Используя метод Эйлера, найти значения функции y, определяемой дифференциальным уравнением y'' = y + y' + 2 при начальных условиях y(0) = 1; y'(0) = 0 шаг h = 0,1. Найти только y1:
     

Правильный ответ:
0,3

499. 
     Используя метод Эйлера, найти значения функции y, определяемой дифференциальным уравнением y''' = xy - y' + y'' + 2 при начальных условиях y(1) = 1; y'(1) = 0; y''(1) = 1 шаг h = 0,1. Найти только y1:
     

Правильный ответ:
1,4

500. 
     По методу Пикара любое приближение решения дифференциального уравнения определяется по формуле …
     

Правильный ответ:

501. 
     По методу Эйлера n - e приближение решения дифференциального уравнения определяется по формуле …
     

Правильный ответ:

502. 
     График решения обыкновенного дифференциального уравнения называется …
     

Правильный ответ:
интегральной кривой

503. 
     По методу Эйлера-Коши приближение решения дифференциального уравнения определяется по формуле …
     

Правильный ответ:

504. 
     Всякое решение, которое может быть получено из общего при определенных числовых значениях произвольных постоянных, входящих в общее решение, называется …
     

Правильный ответ:
частным решением дифференциального уравнения

505. 
     По методу Эйлера-Коши приближение решения дифференциального уравнения определяется по формуле …
     

Правильный ответ:

506. 
     Задача отыскания решения дифференциального уравнения, удовлетворяющего начальным условиям, называется задачей …
     

Правильный ответ:
Коши

507. 
     По методу Рунге-Кутта приближенное решение дифференциального уравнения определяется по формуле …
     

Правильный ответ:

508. 
     Найти абсолютную погрешность равенства: ≈ 0,33.
     

Правильный ответ:
0,0033

509. 
     Дано приближенное число x и его абсолютная погрешность Δ. x = 2,71
     Δ = 0,007. Найти относительную погрешность δ этого числа.
     

Правильный ответ:
0,26%

510. 
     Дано приближенное число x и его относительная погрешность δ.
     x = 25,6 δ = 0,31%. Найти абсолютную погрешность Δ этого числа.
     

Правильный ответ:
0,08

511. 
     Выполнить сложение со строгим учетом погрешностей:
     
     x = 25±0,1 y = 13±0,2 x + y = ?
     

Правильный ответ:
38±0,3

512. 
     Выполнить умножение со строгим учетом погрешностей:
     
     x = 0,17±0,001 y = 6,2±0,05 x · y = ?
     

Правильный ответ:
1,054±0,0147

513. 
     Выполнить вычитание со строгим учетом погрешностей:
     x = 12,7±0,02 y = 10,3±0,01.
     

Правильный ответ:
2,4±0,01

514. 
     Выполнить деление со строгим учетом погрешностей:
     x = 1,428±0,0001 y = 0,14±0,001.
     

Правильный ответ:
10,2±0,075

515. 
     Извлечь корень со строгим учетом погрешности: 156,25±0,001.
     

Правильный ответ:
= 12,500±0,0004

516. 
     Возвести в куб со строгим учетом погрешностей: 1,56±0,003.
     

Правильный ответ:
3,796±0,022

517. 
     Выполнить действия над приближенными числами по правилам подсчета цифр: 25,42 - .
     

Правильный ответ:
642

518. 
     Найти абсолютную погрешность равенства: ≈ 0,14.
     

Правильный ответ:
0,0029

519. 
     Дано приближенное число x и его абсолютная погрешность Δ. x = 3,54 Δ = 0,004. Найти относительную погрешность δ этого числа.
     

Правильный ответ:
0,11%

520. 
     Дано приближенное число x и его относительная погрешность δ.
     x = 17,4 δ = 0,40%. Найти абсолютную погрешность Δ этого числа.
     

Правильный ответ:
0,07

521. 
     Выполнить сложение со строгим учетом погрешностей:
     
     x = 17,1±0,01 y = 16,2±0,03 x + y = ?
     

Правильный ответ:
33,3±0,04

522. 
     Выполнить умножение со строгим учетом погрешностей:
     
     x = 0,17±0,002 y = 6,2±0,01 x · y = ?
     

Правильный ответ:
1,054±0,0147

523. 
     Выполнить вычитание со строгим учетом погрешностей
     x = 12,7±0,07 y = 10,3±0,04.
     

Правильный ответ:
2,4±0,03

524. 
     Выполнить деление со строгим учетом погрешностей
     x = 1,428±0,0002 y = 0,14±0,002.
     

Правильный ответ:
10,2±0,15

525. 
     Извлечь корень со строгим учетом погрешности: 156,25±0,005.
     

Правильный ответ:
= 12,500±0,0002

526. 
     Возвести в куб со строгим учетом погрешностей: 1,56±0,001.
     

Правильный ответ:
3,796±0,007

527. 
     Выполнить действия над приближенными числами по правилам подсчета цифр: 25,412 - .
     

Правильный ответ:
642,91

528. 
     Найти абсолютную погрешность равенства: ≈ 0,059.
     

Правильный ответ:
0,00018

529. 
     Дано приближенное число x и его абсолютная погрешность Δ. x = 17,4 Δ = 0,07. Найти относительную погрешность δ этого числа.
     

Правильный ответ:
0,40%

530. 
     Дано приближенное число x и его относительная погрешность δ.
     x = 3,54 δ = 0,26%. Найти абсолютную погрешность Δ этого числа.
     

Правильный ответ:
0,009

531. 
     Выполнить сложение со строгим учетом погрешностей:
     
     x = 0,27±0,001 y = 0,31±0,002 x + y = ?
     

Правильный ответ:
0,58±0,003

532. 
     Выполнить вычитание со строгим учетом погрешностей:
     x = 12,7±0,01 y = 10,3±0,02.
     

Правильный ответ:
2,4±0,01

533. 
     Выполнить деление со строгим учетом погрешностей:
     x = 1,428±0,0003 y = 0,14±0,005.
     

Правильный ответ:
10,2±0,37

534. 
     Извлечь корень со строгим учетом погрешности: 156,25±0,004.
     

Правильный ответ:
= 12,500±0,0002

535. 
     Возвести в куб со строгим учетом погрешностей: 1,56±0,002.
     

Правильный ответ:
3,796±0,015

536. 
     Выполнить действия над приближенными числами по правилам подсчета цифр: 25,4152 - .
     

Правильный ответ:
643,2

537. 
     Найти абсолютную погрешность равенства: ≈ 0,3.
     

Правильный ответ:
0,014

538. 
     Дано приближенное число x и его абсолютная погрешность Δ. x = 25,6 Δ = 0,08. Найти относительную погрешность δ этого числа.
     

Правильный ответ:
0,31%

539. 
     Дано приближенное число x и его относительная погрешность δ.
     x = 2,71 δ = 0,26%. Найти абсолютную погрешность Δ этого числа.
     

Правильный ответ:
0,007

540. 
     Выполнить сложение со строгим учетом погрешностей:
     
     x = 0,17±0,001 y = 0,19±0,002 x + y = ?
     

Правильный ответ:
0,36±0,003

541. 
     Выполнить вычитание со строгим учетом погрешностей:
     x = 12,7±0,04 y = 10,3±0,07.
     

Правильный ответ:
2,4±0,11

542. 
     Выполнить деление со строгим учетом погрешностей:
     x = 1,428±0,0004 y = 0,14±0,003.
     

Правильный ответ:
10,2±0,22

543. 
     Возвести в куб со строгим учетом погрешностей: 1,56±0,005.
     

Правильный ответ:
3,796±0,037

544. 
     Выполнить действия над приближенными числами по правилам подсчета цифр: 25,412 - .
     

Правильный ответ:
642,91

545. 
     В методе Гаусса приведение системы линейных уравнений к треугольному виду –
     

Правильный ответ:
прямой ход

546. 
     Решить систему линейных алгебраических уравнений можно …
     

Правильный ответ:
Методом Гаусса (по схеме единственного деления)

547. 
     В методе Гаусса для решения систем линейных уравнений последовательное определение неизвестных по формулам –
     

Правильный ответ:
обратный ход

548. 
     Приближенное значение в точке можно вычислить …
     

Правильный ответ:
По формулам Лагранжа

549. 
     Вычисляют интеграл по выбранной квадратурной формуле с шагом n, затем с шагом h/2, т. е. удваивают число шагов –
     

Правильный ответ:
двойной пересчет

550. 
     Приближенное значение определенного интеграла можно найти …
     

Правильный ответ:
По формулам Ньютона-Котеса

551. 
     Способ находить по известному приближению решения следующее, более точное приближение –
     

Правильный ответ:
простая итерация

552. 
     Задачу Коши для дифференциального уравнения можно решить …
     

Правильный ответ:
Методом Эйлера

553. 
     Норма матрицы A = {aij} – это …
     

Правильный ответ:
число

554. 
     Норма 2 матрицы равна …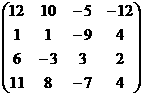
     

Правильный ответ:
30

555. 
     Процесс построения значения корней системы с заданной точностью в виде предела последовательности некоторых векторов называется …
     

Правильный ответ:
итерационным

556. 
     Процесс Зейделя для линейной системы X = β + αX сходится к единственному решению при любом выборе начального приближения, если какая-нибудь из норм матрицы α …
     

Правильный ответ:
меньше единицы

557. 
     Максимальная сумма модулей элементов матрицы по строкам есть …
     

Правильный ответ:
норма 1

558. 
     Норма 3 матрицы равна …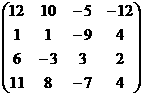
     

Правильный ответ:
28,6356

559. 
     Итерационный процесс построения приближений по формуле называется …
     

Правильный ответ:
методом итерации

560. 
     Процесс Зейделя для линейной системы X = β + αX сходится к единственному решению при любом выборе начального приближения, если …
     

Правильный ответ:
какая-нибудь из норм матрицы α меньше единицы

561. 
     Максимальная сумма модулей элементов матрицы по столбцам есть …
     

Правильный ответ:
норма 2

562. 
     Норма 3 матрицы равна …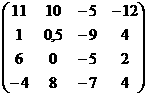
     

Правильный ответ:
26,4244

563. 
     Итерационный процесс построения приближений по формуле называется …
     

Правильный ответ:
методом Зейделя

564. 
     Для оценки погрешности метода Зейделя применяется формула …
     

Правильный ответ:

565. 
     Корень квадратной из суммы квадратов модулей всех элементов матрицы есть …
     

Правильный ответ:
норма 3

566. 
     Норма 2 матрицы равна …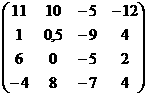
     

Правильный ответ:
26

567. 
     Процесс интеграции для системы X = β + αX сходится к единственному решению независимо от выбора начального вектора, если сумма модулей элементов строк или сумма модулей столбцов …
     

Правильный ответ:
меньше единицы

568. 
     Норма 1 матрицы равна …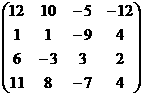
     

Правильный ответ:
39

569. 
     Норма 1 матрицы равна …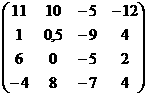
     

Правильный ответ:
38

570. 
     Для оценки погрешности метода итерации применяется формула …
     

Правильный ответ:

571. 
     Формулы для нахождения многочлена, принимающего в данных точках xi(i=0; 1; … n) данные значения Pn(xn) называются:
     

Правильный ответ:
интерполяционными

572. 
     Интерполяционный многочлен Ньютона находится по формуле
     Pn(x) = …
     

Правильный ответ:

573. 
     Интерполяционный многочлен, соответствующей таблице:
     y = 2x2 – 5x +1. Найти: y0; y1; y2.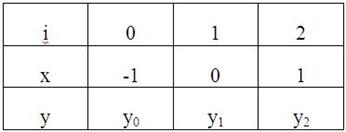
     

Правильный ответ:
8; 1; -2

574. 
     Какой интерполяционный многочлен соответствует таблице: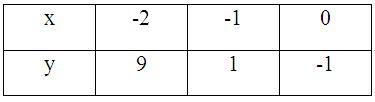
     

Правильный ответ:
y = 3x2 + x - 1

575. 
     Какой интерполяционный многочлен соответствует таблице: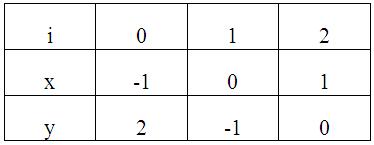
     

Правильный ответ:
y = 2x2 - x - 1

576. 
     Функция задана таблицей: Найти Δ2y0.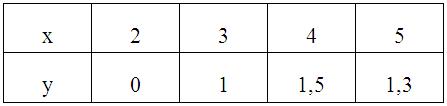
     

Правильный ответ:
-0,5

577.