Метод годунова. Численный метод Годунова первого порядка точности. Численный метод Годунова первого порядка точности
 Скачать 161 Kb. Скачать 161 Kb.
|
|
Численный метод Годунова первого порядка точности. Известно, что решение задачи взаимодействия ударных волн, которая описывается гиперболическими системами уравнений, может быть гладким в одних областях и разрывным в других. Такие свойства решений налагают на алгоритмы численного решения гиперболических систем уравнений достаточно противоречивые требования. С одной стороны, численный метод должен уметь сохранять свойство монотонности в тех областях, где искомые решения имеют большие перепады значений. С другой стороны, тот же метод должен обладать высоким порядком точности в тех областях, где решение является гладким. Теорема Годунова показывает, что в рамках линейных разностных схем эти два требования одновременно удовлетворены быть не могут. Для преодоления этих трудностей воспользуемся конечно-объемной схемой аппроксимирующей гиперболические системы уравнений, записанные в интегральной форме и выражающие законы сохранения. В этом случае, несмотря на ошибки аппроксимации, схема обеспечивает точное выполнение законов сохранения в расчетной области, при записи их в дивергентном виде. К таким схемам относится численный метод решения уравнений газовой динамики предложенный С. К. Годунов, который существенно основан на использовании точного или приближенного решения задачи Римана (.**.1), (**.2). 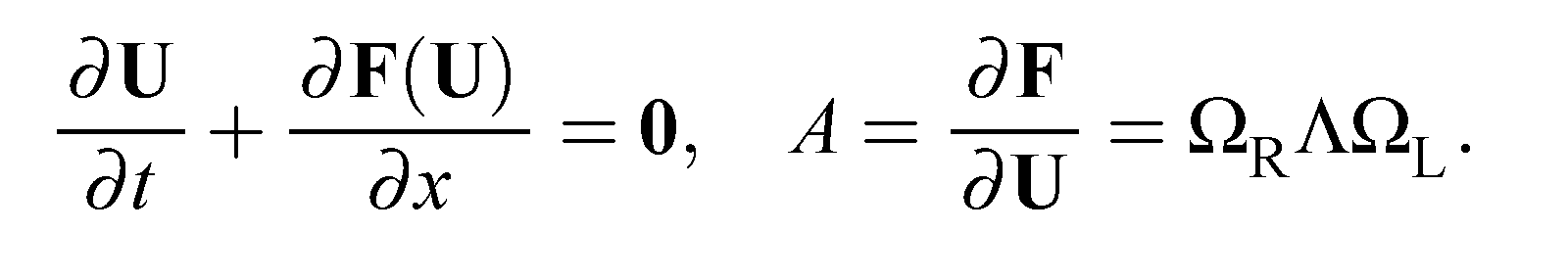 **.1 **.1Здесь U = U(t,x) = [U1...,Un]T, F(U) = [F1... ,Fn]T, t ≥ 0, -∞ 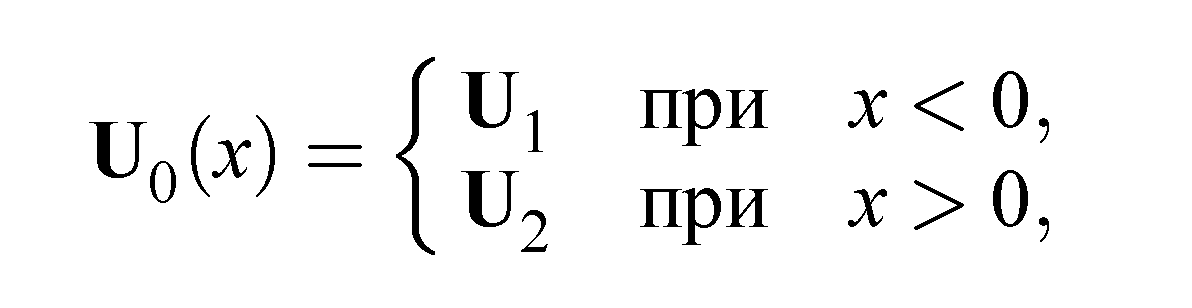 **.2 **.2где U1 и U2 - постоянные векторы. Этот метод формулируется следующим образом. Рассмотрим равномерную пространственную сетку с шагом Δх. Значения сеточной функции будем обозначать как 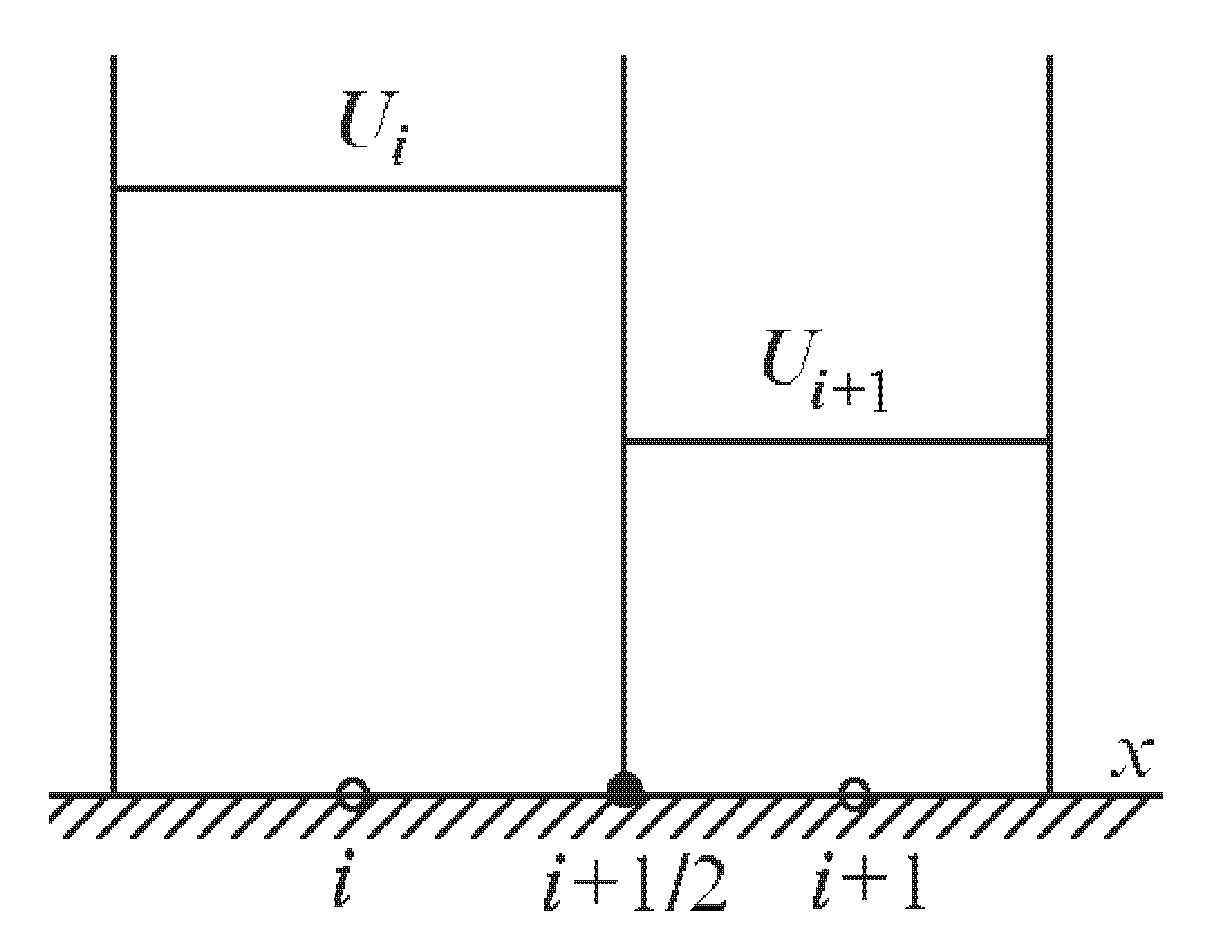 Рисунок. ***. Кусочно-постоянное распределение функции U Полуцелые нижние индексы i±1/2 обозначают значения сеточной функции на границе между ячейками с номерами i и i ± 1. Верхний целый индекс k = 0,1,2,... обозначает номер слоя (шага) по времени. Положим, что все сеточные функции являются постоянными внутри каждой из дискретных ячеек (рис. 2.1). Тогда на границе с номером i + 1 /2 на каждом шаге по времени будем решать задачу Римана со следующими начальными данными: 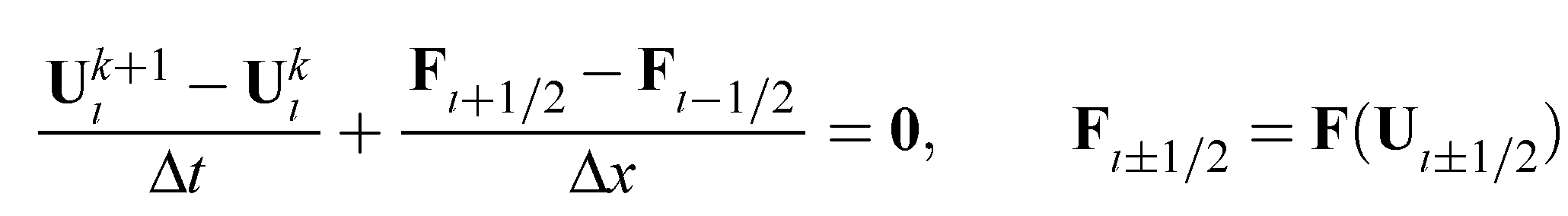 **.3 **.3Здесь Δt — шаг по времени; 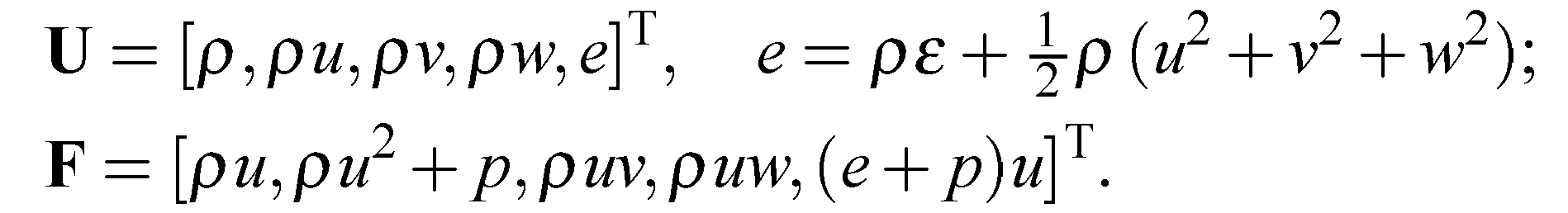 Эта схема обладает первым порядком точности по времени и по пространству. Условие устойчивости схемы имеет вид 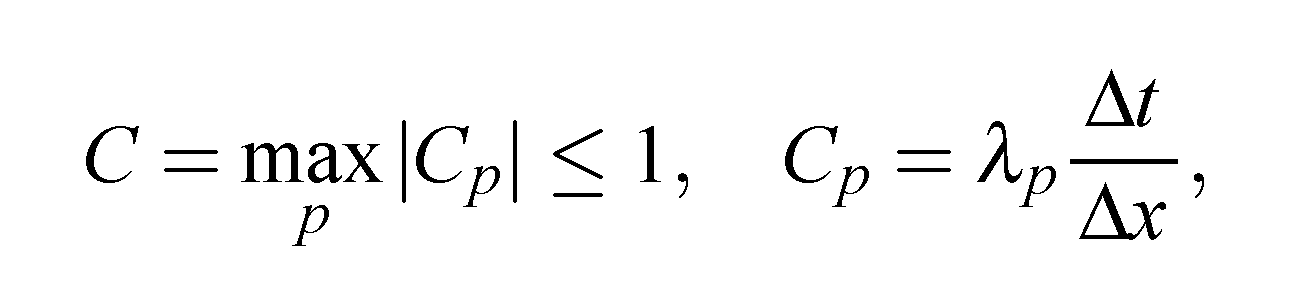 **.4 **.4где λр — собственные значения якобиевой матрицы А для уравнений (**.1). Неравенство (**.4) называется условием устойчивости Куранта-Фридрихса-Леви (Courant, Friedrichs, Lewy, 1928), а С — числом Куранта. Физическая интерпретация условия устойчивости состоит в обеспечении того, чтобы малые возмущения, распространяющиеся от одной границы дискретной ячейки, за время Δt не достигли другой. Метод Годунова для уравнений газовой динамики в случае трехмерного пространства Интегральная форма уравнений газовой динамики имеет вид Здесь G — это конечная область в трехмерном пространстве (x,y,z), dG = dxdydz — элемент объема, S—поверхность, ограничивающая область G, dS = n dS— ориентированный элемент поверхности S, где n — внешняя нормаль к S, a dS—элемент площади; а • b обозначает скалярное произведение двух векторов а и b. Для построения схемы Годунова для уравнений (**.5-**.7), записанных в интегральной форме, применим метод конечных объемов, который также называют интегро- интерполяционным методом. Для этого покроем всю вычислительную область дискретными ячейками состоящими из произвольных выпуклых конечных многогранников с объемами Gl где l = 1,2,..., и с числом граней m = m(i), каждая из которых имеет площадь Sj, где j = 1,..., m(i). Аппроксимируем интегральные уравнения в каждом из многогранников следующим образом: 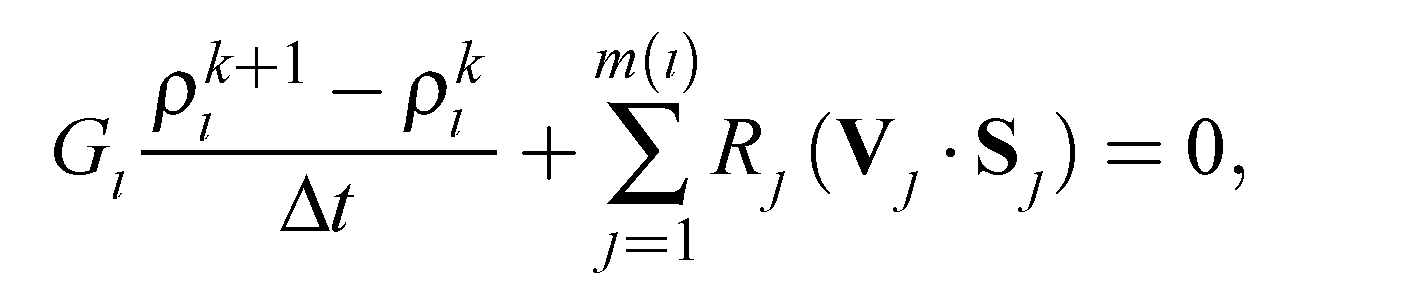 **.8 **.8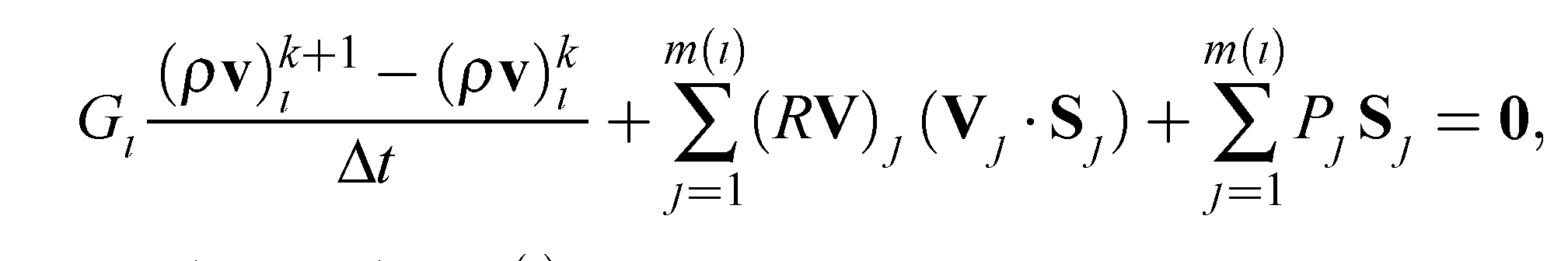 **.9 **.9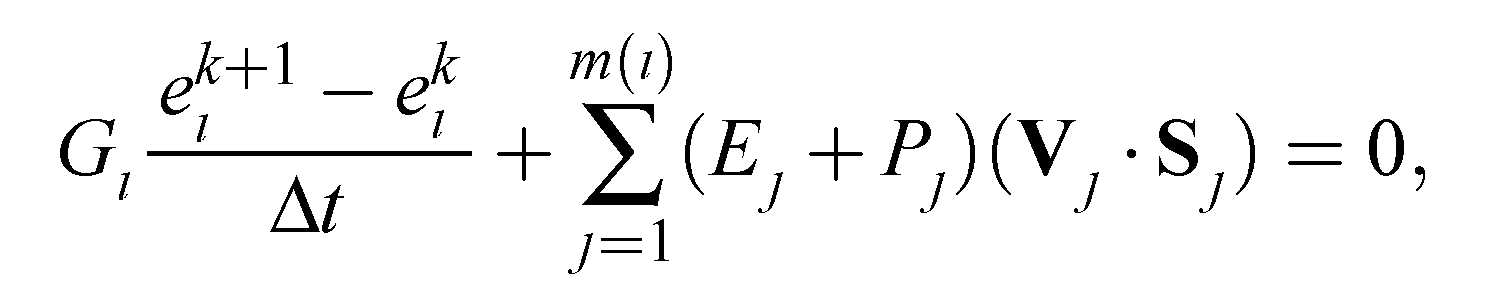 **.10 **.10где Sj = njSj, a Δt — шаг по времени. Нижний целый индекс i в уравнениях (**.8- **.10) обозначает величины функций, отнесенные к центру масс i -го многогранника, а нижний целый индекс j обозначает величины функций, отнесенные к центру j -й грани дискретной ячейки. Верхний целый индекс к обозначает номер шага по времени. Соответствующие большие буквы в формулах обозначают плотность R, скорость V, давление Р и полную энергию Е на гранях дискретной сеточной ячейки. Эти "большие" величины вычисляются путем решения задачи Римана для уравнений газовой динамики на этих гранях. Все возможные конфигурации решения суммированы в таблице Таблица **.1. Конфигурации точного решения задачи Римана о распаде произвольного газодинамического разрыва   |
