ПАРНАЯ РЕГРЕССИЯ И КОРРЕЛЯЦИЯ. Парная регрессия и корреляция
 Скачать 135.71 Kb. Скачать 135.71 Kb.
|
|
Федеральное государственное бюджетное образовательное учреждение высшего образования «ОМСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ» Кафедра "Математические методы и информационные технологии в экономике" ЗАДАНИЕ № 1 по дисциплине «Эконометрика» на тему ПАРНАЯ РЕГРЕССИЯ И КОРРЕЛЯЦИЯ Выполнил ст. гр. ПИ- ПИ-192___ Шарапов К. В. "____"___________2022 г. Принял ст.пр. Шевелева О.Г. "____"___________2022 г. Омск 2022 Вариант 3 Данные для расчётов:
Рис 1. Таблица с исходными данными Требуется: 1. Для характеристики зависимости y от x рассчитать параметры следующих функций: а) линейной; б) степенной; в) показательной; г) равносторонней гиперболы. 2. Оценить каждую модель с помощью средней ошибки аппроксимации  и F-критерия Фишера. и F-критерия Фишера.3. Построить графики исходной и расчетной зависимости, выбрав подходящий тип диаграммы. Для линейной и степенной функции добавить линию тренда для исходных данных, сравнить уравнение линии тренда с рассчитанными функциями. Линейная функция 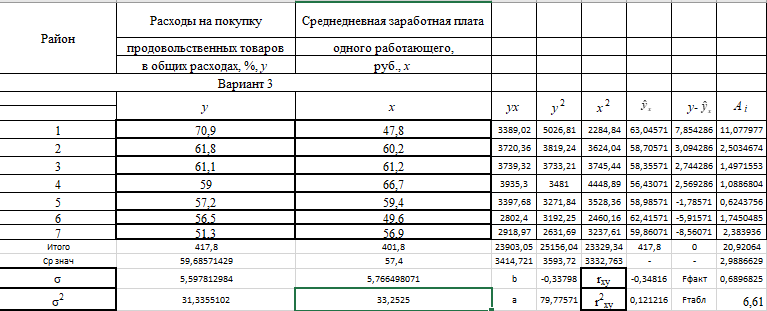 Рис 2. Таблица расчётов линейной функции 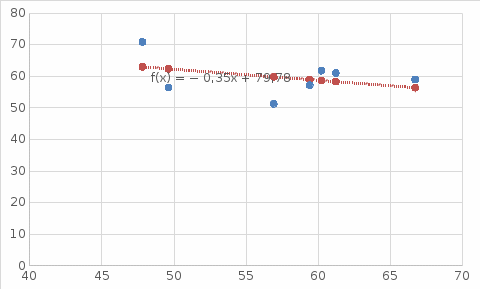 Рис 3. График функции Линейный коэффициент парной корреляции: -0,35 Можем сделать вывод, что связь слабая прямая Вариация результата: 12,12% Fфакт = 0,68 < Fтабл = 6,61, = 0,05, v1 = m = 1, v2 = n – m – 1= 7 – 1 – 1 = 5. Следовательно, принимается гипотезаH0 о статистически незначимых параметрах этого уравнения. Этот результат можно объяснить сравнительно невысокой теснотой выявленной зависимости и небольшим числом наблюдений. Степенная функция 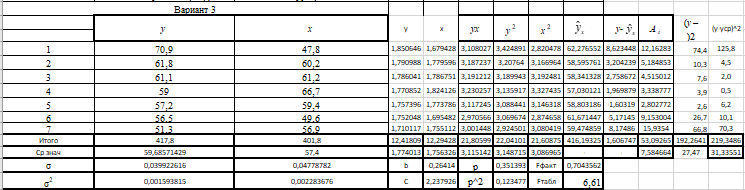 Рис 4. Таблица расчётов степенной функции 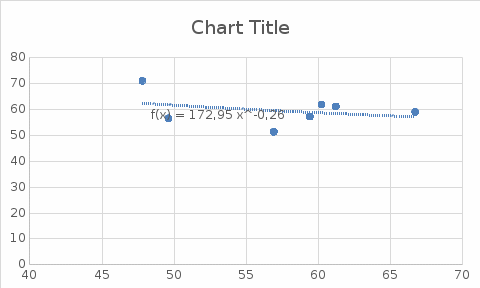 Рис 5. График степенной функции p = 0,35 - связь слабая Fфакт =0.7 < Fтабл = 6,61, = 0,05. Принимается гипотеза H0 о статистически незначимых параметрах этого уравнения. Характеристики степенной модели указывают, что она несколько лучше линейной функции описывает взаимосвязь. Показательная функция 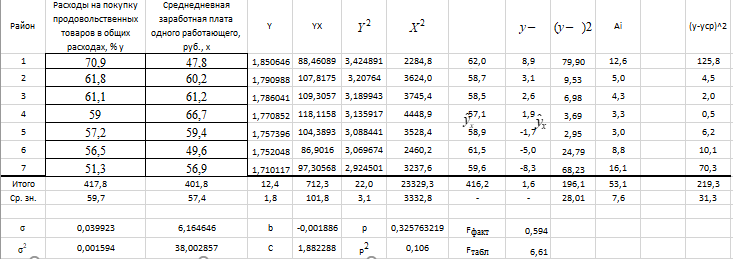 Рис 6. Таблица расчётов показательной функции 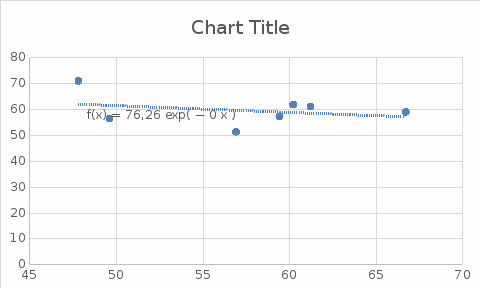 Рис 7. График для показательной функции 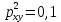 связь слабая. связь слабая.Fфакт=0,594< Fтабл = 6,61, = 0,05. Принимается гипотеза H0 о статистически незначимых параметрах этого уравнения. Показательная функция чуть хуже, чем степенная описывает изучаемую зависимость. Равносторонняя гипербола 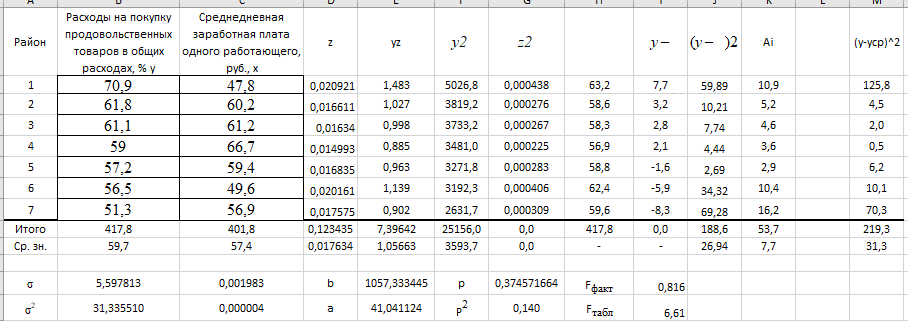 Рис 8. Таблица расчётов для равносторонней гиперболы 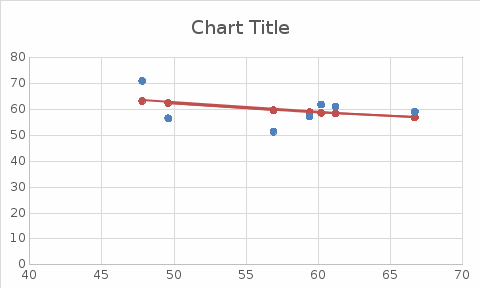 Рис 9. График для функции равносторонняя гипербола Связь слабая. 2xy = 0,14 По уравнению равносторонней гиперболы получена наибольшая оценка тесноты связи по сравнению с линейной, степенной и показательной регрессией. Fфакт = 0.816< Fтабл = 6,61, = 0,05. Следовательно, принимается гипотеза H0 о статистически незначимых параметрах этого уравнения. Этот результат можно объяснить сравнительно невысокой теснотой выявленной зависимости и небольшим числом наблюдений. Вывод При оценке критериев с помощью парной регрессии и корреляции можно сделать вывод, что не один из методов Фишера не принимает данную гипотезу, но наиболее точным является метод равносторонняя гипербола. |
