1) ЧП. Классификация.
ЧП – цепь, имеющая две пары внешних выводов (четыре полюса) с помощью которых он может присоединиться к другим цепям или источникам. Четырехполюсниками являются фильтры, трансформаторы, усилители, каскады радиопередатчиков и радиоприемников, линии связи и т. д.
Классификация: активные, пассивные, линейные, нелинейные, симметричные, несимметричные, автономные, неавтономные.
|
2) Уравнения четырехполюсников (в y-, z-, a-, b-, h- и g-параметрах)
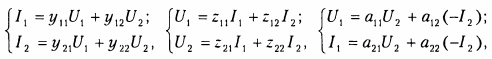
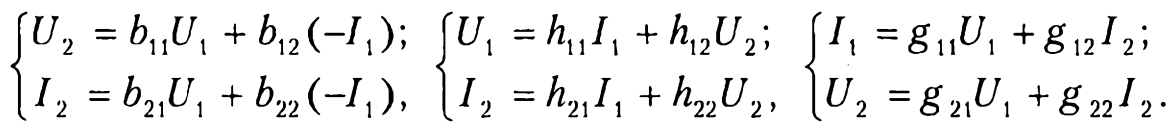
|
3) Схемы замещения четырехполюсников (Г-, П-и Т-образные, мостовые)
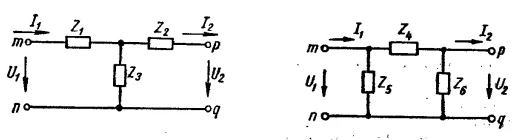 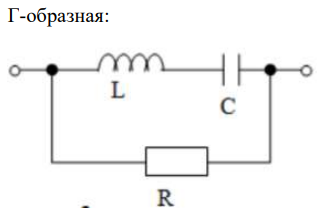
|
4) Входное сопротивление четырехполюсника.
Сопротивление холостого хода и четырехполюсника
Входное сопротивление четырехполюсника. Если к одной паре зажимов четырехполюсника подключить произвольное сопротивление, то со стороны другой пары зажимов четырехполюсник можно рассматривать как двухполюсник с входным сопротивлением, которое называют входным сопротивлением четырехполюсника. Zвх = U1 / I1
|
5) Уравнения передачи четырехполюсника
- Свойства ЧП как системы передачи энергии полностью определяются соотношениями между напряжениями на входе и выходе и токах I1 и I2.
Передача по U: Hu = U2 / U1 , По I: Hi = I2 / I1
|
6) Соединения четырехполюсника. Регулярные соединения.
|
7) Цепи с зависимыми источниками
Для пассивных цепей, составленных из RLC-элементов и независимых источников, справедлив принцип взаимности (обратимости) у12 = у21. На практике, однако, преобладают цепи, где этот принцип несправедлив. Такие цепи называют
активными (необратимыми) цепями, а схемы их замещения обязательно содержат хотя бы один необратимый элемент, называемый зависимым источником.
10) Постоянная передачи четырехполюсника. Собственное ослабление и фазовая постоянная.
Постоянная передачи Г — это комплексная безразмерная величина характеризует изменение напряжения и тока при согласованной нагрузке как по значению, так и по фазе.
Собственное ослабление — это физическая безразмерная величина ее единицей измерения служит непер (Нп), характеризует как отношение напряжений, так и отношение токов на входных и выходных выводах и показывает ослабление абсолютных значений напряжения и тока.
Фазовая постоянная – это сдвиг по фазе между токами, который равен сдвигу фаз между напряжениями.
14) k- и m-фильтры
|
8) Необратимые четырехполюсники
У необратимых ЧП независимы все 4 параметра, поэтому эквивалентная схема замещения необратимого ЧП должна содержать 4 элемента, из которых хотя бы один — зависимый источник.
Схемы и формулы:
11) Уравнение передачи четырехполюсника в собственных (характеристических) параметрах.
12) Фильтры
Фильтр – ЧП, у которого в некоторой полосе частот, находящейся в районе максимума АЧХ и называемой полосой пропускания (ПП), сигналы проходят на выход с малым затуханием, а в остальной полосе частот сигналы на выход практически не проходят. Граничные частоты ПП называются частоты среза. При идеализации частотных характеристик (ЧХ) часто используют понятие идеальных фильтров, у которых в полосе пропускания A(ω)=K=const или A(ω)=1, а в полосе задержания (ПЗ) A(ω)=0.
13) Классификация фильтров по пропускаемому спектру частот
1. Фильтр нижних частот
2. Фильтр высоких частот
3. Полосовой пропускающий фильтр
4. Полосовой заграждающий фильтр
|
9) Собственные (характеристические) параметры четырехполюсника
Собственное (характеристическое) сопротивление четырехполюсника. При передаче сигналов на большие расстояния электрическая цепь может состоять из большого числа каскадно включенных четырехполюсников. Основным требованием к передающей цепи является обеспечение минимальных потерь мощности передаваемого сигнала в самой цепи при условии, что мощность сигнала, выделяемая в нагрузке на приемном конце, должна быть максимально возможной.
Известно, что генератор сигналов с внутренним сопротивлением Zг, отдает максимальную мощность в такую нагрузку, сопротивление которой Zн согласованно с его внутренним сопротивлением, т.е. при Zг = Zн. Для выполнения этого условия необходимо обеспечить передачу максимальной мощности от генератора в четырехполюсник и передачу максимальной мощности от четырехполюсника в нагрузку. Это означает, что необходимо согласовать входное сопротивление четырехполюсникаZвх1 с внутренним сопротивлением генератора, т.е. выполнить условие Zвх1 = Zг и согласовать входное сопротивление четырехполюсника Zвх2 с сопротивлением нагрузки, т.е. выполнить условие Zвх2 = Zн. Если при включении четырехполюсника выполняется условие Zвх1=Zг и Zвх2 = Zн, то четырехполюсник будет работать в режиме согласованного включения.
Входные сопротивления четырехполюсника Zвх1 и Zвх2, при которых наступает режим согласованного включения, называются собственными (характеристическими) сопротивлениями четырехполюсника и обозначаются Zс1 и Zс2.
Формулы:
|
15) Безындукционные фильтры
Не содержат L-элемент, не содержат индуктивных катушек. Применяют, когда сопротивление нагрузки велико по сравнению с сопротивлением фильтра. Также применяют для низких частот, дабы не изготавливать катушки с высокой добротностью.
|
1) Нелинейные электрические цепи постоянного тока.
Нелинейными называются цепи, в состав которых входит хотя бы один нелинейный элемент. Нелинейными называются элементы, параметры которых зависят от величины и (или) направления связанных с этими элементами переменных (напряжения, тока, магнитного потока, заряда, температуры, светового потока и др.).
|
2) Особенности расчета нелинейных электрических цепей постоянного тока: статические и дифференциальные параметры НЭ, замена нелинейного сопротивления эквивалентным линейным сопротивлением и ЭДС
Цепь, содержащая хотя бы один нелинейный элемент, называется нелинейной. Параметры НЭ зависят от значений его токов или напряжений, например, RНЭ(i) или GНЭ(i). Основной особенностью является расчёт двумя способами графическим и аналитическим.
Графический метод эффективен при расчете простых цепей, в частности, с одним нелинейном элементом В начале метода находятся все результирующую ВАХ далее определение всех рабочих точек на всех ВАХ при определённом значение.
Аналитический метод последовательность расчета: 1. Аппроксимируют ВАХ НЭ удобным аналитическим выражением. 2. Составляют систему независимых уравнений Кирхгофа, т.е. записывают уравнение соединения. 3. Исключают из системы промежуточные переменные и находят нелинейное функциональное уравнение для отыскания реакции
|
3) Графический метод расчета нелинейных электрических цепей постоянного тока
|
4) Нелинейные магнитные цепи постоянного тока
Магнитная цепь – совокупность элементов, возбуждающих магнитное поле (пост. магниты, катушки), и магнитопроводов, а также ферромагнитных тел, образующих замкнутые пути основной части линий магнитного поля, предназначенные для создания магнитного поля определенной интенсивности магн. инд. B, конфигурации и направления. (Лановенко)
Совокупность объектов, включающих ферромагнитные тела, по которым при наличии магнитодвижущей силы (МДС) замыкаются линии магнитной индукции, называется магнитной цепью. (Учебник ТОЭ)
|
5) Законы нелинейных магнитных цепей постоянного тока: закон полного тока, закон Ома, законы Кирхгофа
Закон полного тока: Количественная связь между линейным интегралом от вектора напряженности Н, вдоль любого проводящего контура длинной L и алгебраической суммой токов, охваченными этим контуром определяется как: 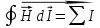
Закон Ома для магнитной цепи:
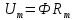 , Этот способ неудобен, т.к. нужно считать напряжение на каждой цепи, поэтому используют Закон Кирхгофа , Этот способ неудобен, т.к. нужно считать напряжение на каждой цепи, поэтому используют Закон Кирхгофа
Закон Кирхгофа для магнитных цепей Первый закон: Алгебраическая сумма магнитных потоков в узле равна нулю:
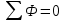
Второй закон: Алгебраическая сумма магнитных напряжений на каждом участке магнитного контура, равна сумме МДС каждого контура.
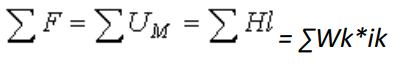
|
6) Порядок расчета нелинейных магнитных цепей постоянного тока.
Первый закон Кирхгофа для магнитных цепей – алгебраическая сумма магнитных потоков в узле магнитной цепи равна нулю. Закон полного тока применяется к замкнутому контуру, образованному средними магнитными линиями магнитной цепи.
Второй закон Кирхгофа для магнитных цепей – алгебраическая сумма магнитных напряжений в замкнутом контуре магнитной цепи равна алгебраической сумме магнитодвижущих сил в том же контуре.
Алгоритм прямой задачи расчета неразветвленной магнитной цепи 1. Разбиваем магнитную цепь на однородные участки постоянного сечения и определяем длины lk и площади поперечного сечения Sk участков. Длины участков берем по средней силовой линии. 2. Исходя из постоянства потока вдоль всей неразветвленной магнитной цепи, по заданному магнитному потоку Ф и сечениям Sk участков находим магнитные индукции на каждом участке: 3. По найденным магнитным индукциям Bk участков цепи и кривой намагничивания материала kго участка цепи определяем напряженности поля Hk на каждом участке магнитной цепи. 4. Подсчитаем сумму падений магнитных напряжений UMk=Hklk вдоль всей магнитной цепи
|
7) Нелинейные электрические цепи переменного тока: разновидности, особенности таких цепей
Нелинейными электрическими цепями переменного тока называют электрические цепи переменного тока, в состав которых входит один или несколько нелинейных элементов.
Нелинейными электрическими цепями переменного тока называются цепи, в состав которых входят один или несколько нелинейных сопротивлений (нелинейных элементов) переменного тока.
Характерной чертой нелинейных элементов переменного тока являются нелинейная-амперная, кулон-вольтная, вебер-амперная и другие характеристики.
Переменному току оказывают сопротивление активные сопротивления, индуктивности и ёмкости.
В соответствии с этим нелинейные сопротивления переменного тока могут быть разделены на три группы:
1) группа нелинейных активных сопротивлений;
2) группа нелинейных индуктивных сопротивлений;
3) группа нелинейных емкостных сопротивлений.
|
8) Особенности цепей с нелинейным активным сопротивлением
Эти сопротивления имеют нелинейную вольтамперную характеристику U = I(i). В качестве нелинейных активных сопротивлений широкое распространение получили полупроводниковые выпрямители, лампы накаливания, магнитные усилители и др. Группа этих нелинейных элементов способствуют созданию несинусоидальных токов в электрических цепях;
9) Особенности цепей с нелинейным индуктивным элементом
Под нелинейными индуктивными элементами понимают индуктивные катушки (индуктивности) с обмотками, намотанными на замкнутые сердечники из ферромагнитного материала, для которых зависимость магнитного потока в сердечнике от протекающего по обмотке тока нелинейна. Индуктивное сопротивление таких катушек, оказываемое прохождению переменного тока, не постоянно; оно зависит от значения переменного тока. Условимся называть их нелинейными индуктивными катушками или нелинейными индуктивностями.
Нелинейные индуктивности подразделяют на управляемые и неуправляемые, но деление на безынерционные и инерционные на них не распространяется, так как их нелинейность обусловлена свойствами ферромагнитного материала, а не тепловым эффектом.
|
10) Особенности цепей с нелинейным емкостным элементом
В обычных конденсаторах обкладки разделены веществом, диэлектрическая проницаемость которого не является функцией напряженности электрического поля. Для них зависимость мгновенного значения заряда q на одной обкладке от мгновенного значения напряжения и между
|
обкладками (кулон-вольтная характеристика) представляет собой прямую линию (рис. 15.5), а их емкость не зависит от напряжения и. Для нелинейных конденсаторов зависимость q от и нелинейна (рис. 15.6).
Нелинейные конденсаторы называют еще варикондами. На электрических схемах вариконды изображают в соответствии с рис. 15.7, а.
|
Пространство между обкладками вариконда заполняют сегнетодиэлектриком. Сегнетодиэлектриками называют вещества, диэлектрическая проницаемость которых является функцией напряженности электрического поля. Название «сегнетодиэлектрики» им присвоено потому, что впервые это свойство было обнаружено у кристаллов сегнетовой соли.
|
1) Электромагнитное поле. Уравнения Максвелла. Физический смысл уравнений Максвелла
Электромагнитное поле - это фундаментальное физическое поле, взаимодействующее с электрически заряженными телами, представимое как совокупность электрического и магнитного полей, которые могут при определенных условиях порождать друг друга. Электромагнитное поле (его изменение со временем) описывается в электродинамике в классическом приближении посредством системы уравнений Максвелла.
Уравнения Максвелла Уравнения Дж. Максвелла создают основу для предложенной им теории электромагнитных явлений, которая объяснила все известные в то время эмпирические факты, некоторые эффекты предсказала. Главным выводом теории Максвелла стало положение о существовании электромагнитных волн, которые распространяются со скоростью света.
Физический смысл уравнений Максвелла Уравнение (1) системы указывает на то, что двумя возможными источниками магнитного поля являются токи проводимости (j→) и токи смещения (∂D→/∂t). Уравнение (2) является законом электромагнитной индукции и отображает тот факт, что переменное магнитное поле - один из источников возникновения электрического поля. Следующим источником электрического поля служат электрические заряды, что и отображает уравнение (4), которое является, по сути, законом Кулона. Уравнение (3) означает, что линии магнитной индукции не имеют источников (они либо замкнуты, либо уходят в бесконечность), что приводит к выводу об отсутствии магнитных зарядов, которые создают магнитное поле.
|
2) Электростатическое поле. Закон Кулона
Электростатическое поле и заряды существуют в идеальном диэлектрике, вообще лишенном проводимости (γ = 0). Внутри проводящих тел поле отсутствует, а заряды располагаются на поверхности тел.
Закон Кулона Два точечных заряда q1 и q2 в вакууме взаимодействуют друг с другом с силой F , прямо пропорционально произведению зарядов q1 и q2м обратно пропорциональна квадрату расстояний R между ними. Эта сила направлена по линии, соединяющей точечные заряды (рис1). Заряды имеющие одинаковые знаки стремятся оттолкнуться друг от друга, а заряды противоположных знаков сблизиться.
3) Напряженность электрического поля. Силовые линии
Характеристикой ЭП является именно напряжённость, так как она зависит только от заряда, создающего поле, внесённый пробный заряд на неё не влияет.
Силовые линии электростатического поля имеют следующие свойства: 1. Всегда незамкнуты: начинаются на положительных зарядах (или на бесконечности) и заканчиваются на отрицательных зарядах (или на бесконечности). 2. Не пересекаются и не касаются друг друга. 3. Густота линий тем больше, чем больше напряжённость, то есть напряжённость поля прямо пропорциональна количеству силовых линий, проходящих через площадку единичной площади, расположенную перпендикулярно линиям.
|
4) Потенциал. Связь напряженности и потенциала
Потенциал произвольной точки может быть взят как работа, совершенная силами поля по переносу единичного заряда из данной точки поля в точку с нулевым потенциалом (бесконечно далека). Эквипотенциальные поверхности – совокупность т-к поля, имеющих один и тот же потенциал. Если мысленно рассечь электростат. поле какой-либо секущей поверхностью, то в полученном сечении можно наблюдать эквипотенциальные линии. Эквипотенциальные линии и силовые линии в любой т-ке поля пересекаются под углом в 90°. Эквипотенциальные линии замыкаются сами на себя.
Напряжённость в какой-либо точке электрического поля равна градиенту потенциала в этой точке, взятому с обратным знаком. Знак «минус» указывает, что напряженность E направлена в сторону убывания потенциала
5) Уравнения Пуассона и Лапласа для электростатики
7) Поле внутри проводящего тела
Все точки поверхности проводящего тела имеют 1 и тот же потенциал => между 2 любыми близкими точками ∆𝜑 = 0, но так же ∆𝜑 = 𝐸𝑡𝑑𝑙 = 0, т.к. 𝑑𝑙 ≠ 0 → 𝐸𝑡 = 0, 𝐸 = 𝐸𝑛 = − 𝑑𝜑′′ 𝑑𝑛 , где n – нормаль. Всегда отсутствует тангенсальная составляющая. Внутри проводящего тела 𝐸⃗ = 0, т.к. 𝐸𝑡 = 0 внешнее поле компенсируется полем зарядов, расположенных на поверхности тела (разделение зарядов => электро-магнитной индукции) Отрицательные заряде смещаются на поверхность, обращенную в сторону более высокого потенциала
|
8) Условия на границе раздела проводящего тела и диэлектрика в электростатике
|
9) Условия на границе раздела двух диэлектриков в электростатике.
|
10) Электрическая емкость. Емкости простейших систем
Электрическая емкость. Емкости простейших систем. Для проводников электрической ёмкостью называется величина, которая характеризует способность тела накапливать электрический заряд, Электроемкость любого предмета зависит от его формы и геометрических размеров. С = q /
где q - заряд, - потенциал, емкость измеряется в Фарадах (Кл/В)
Одной из простейших систем является конденсатор – это такая система, где проводящие тела находятся в диэлектрике, а заряды тел равны по величине и обратны по знаку, а потенциалы – U1 и U2
|
11) Метод зеркальных изображений
Используется для расчёта полей, ограниченных какой-либо проводящей поверхностью правильной формы или границей между двумя д/э правильной формы. Поле прямоугольного заряда с плотностью +τ, расположенном на расстоянии h от проводящей среды. Мысленно устраним проводящую среду и заменим её заряженным проводом, являющимся зеркальным изображением реального провода, но с противоположным знаком. Рассчитанное по двухпроводной системе поле справедливо для исходного задания в верхней п/плоск.
|
12) Электрическое поле постоянных токов. Виды токов
Постоянный ток — это физический процесс, заключающийся в равномерном движении электрических зарядов в проводнике под действием постоянного электрического поля
Электрическое поле постоянного тока, как и поле электростатическое, является потенциальным, безвихревым и напряженность такого поля направлена в сторону убывания потенциала.
Виды токов: 1. Ток проводимости. 2. Ток смещения. 3. Ток переноса.
|
13) Закон Ома в дифференциальной форме.
|
14) Законы Кирхгофа в дифференциальной форме
|
15) Закон Джоуля-Ленца в дифференциальной форме
|
16) Уравнения Лапласа для электрического поля в проводящей среде
|
17) Условия на границе раздела двух проводящих тел. Следствия условий
При переходе тока через поверхность раздела сред с различными удельными проводимостями g1 и g2 направление тока изменяется, если только линии тока не направлены нормально к поверхности раздела (рис. 2.1). При этом, на поверхности раздела равны между собой касательные составляющие напряженности поля
20) Закон полного тока в интегральной и дифференциальной формах
|
18) Метод электростатической аналогии
Аналогия электростатического поля в области, где нет свободных зарядов, и поля стационарных токов в проводящих средах, где нет сторонних сил, обусловлена полной аналогией соответствующих уравнений и граничных условий
Таблица:
21) Принцип непрерывности магнитного потока
|
19) Магнитное поле постоянных токов. Основные силовые характеристики
Магнитное поле образуется только вокруг движущихся электрических зарядов, и его действие распространяется тоже лишь на движущиеся заряды. Магнитное и электрические поля неразрывны и образуют совместно единое электромагнитное поле. Всякое изменение электрического поля приводит к появлению магнитного поля и, наоборот, всякое изменение магнитного поля сопровождается возникновением электрического поля. Графически магнитное поле изображают магнитными силовыми линиями, которые проводят так, чтобы направление силовой линии в каждой точке поля совпадало с направлением сил поля; магнитные силовые линии всегда являются непрерывными и замкнутыми.
Величиной, характеризующей магнитные свойства среды, служит абсолютная магнитная проницаемость. Единицей ее измерения является генри на метр (1 Гн/м = 1 Ом*с/м). В среде с большей магнитной проницаемостью электрический ток определенной силы создает магнитное поле с большей индукцией. Напряжённость магнитного поля, векторная физическая величина (Н), являющаяся количественной характеристикой магнитного поля. Н. м. п. не зависит от магнитных свойств среды. В вакууме Н. м. п. совпадает с магнитной индукцией В
|
22) Скалярный потенциал магнитного поля
|
23) Векторный потенциал магнитного поля
|
24) Уравнения Пуассона для вектора А
|
25) Условия на границе раздела двух сред с различными 𝜇
29) Индуктивность.
30) Уравнения Максвелла в комплексной форме
|
26) Векторный потенциал элемента с током
Векторный потенциал – это векторное поле, ротор которого равен заданному векторному полю. Известны математические выражения, описывающие векторный потенциал в виде поля вектора А, существующего в окрестности объемного или линейного токовых элементов.
Векторный потенциал по размерности и по системному расположению связан с силой тока смещения через магнитную постоянную и они оба имеют совпадающее направление то есть векторного потенциала то же направление что и у вектора плотности тока смещения, на основании того что магнитная индукция – это ротор векторного потенциала, а произведение магнитной индукции на площадь есть магнитный поток, то циркуляция векторного потенциала по контуру образует поток его ротора проходящего через поверхность, натянутую на этот контур и этот поток называется магнитным потоком.
31) Теорема Умова-Пойнтинга для мгновенных значений
|
27) Магнитное экранирование
МАГНИ́ТНОЕ ЭКРАНИ́РОВАНИЕ, предназначено для уменьшения напряжённости постоянного или низкочастотного магнитного поля в к.-л. области пространства либо для локализации магнитного поля в заданной области пространства. Производится путём помещения этой области в замкнутую оболочку из ферромагнитных материалов. Ослабление магнитного поля до его полного исчезновения невозможно.
28) Метод зеркальных изображений для магнитного поля постоянных токов
Метод применяют для расчета магнитных полей в неферромагнитных средах, ограниченных какой-либо ферромагнитной поверхностью правильной формы или в которых есть геометрически правильной формы граница между двумя средами с различными магнитными проницаемостями. Рассмотрим поле прямолинейного провода с током I, расположенным на расстоянии h от плоской ферромагнитной поверхности (рис. 3.35). Устраним мысленно ферромагнитную среду и заменим ее проводом, являющимся зеркальным изображением реального провода в поверхности раздела и имеющим ток такого же направления и такой же величины, как и ток реального провода (рис. 3.35). Действительный провод и его зеркальное изображение составляют двухпроводную линию. Поле от такой системы проводников с токами в области над проводящей средой останется таким же, как и в действительных условиях. В этом и заключается метод зеркальных изображений.
|
32) Теорема Умова-Пойнтинга в комплексной форме
|
33) Переменное электромагнитное поле в проводящей среде
Переменное электромагнитное поле – это совокупность изменяющихся во времени и взаимно связанных и обуславливающих друг друга электрического и магнитного полей. Оно определяется двумя векторными величинами напряженностью электрического поля E и напряженностью магнитного поля H .
|
35) Плоская электромагнитная волна
Плоская электромагнитная волна - в общем случае под э/м волной понимают волну, векторы которой распложены в плоскости XoY┴Z и изменяется только в ф-ии z времени t.
|
36) Распространение плоской электромагнитной волны в проводящем полупространстве
|
37) Электромагнитное экранирование
Принцип действия электромагнитного экранирования иллюстрируется на рисунке 6. Если на пути равномерного переменного магнитного поля (рисунок 6, а) поместить медный цилиндр (экран), то в нем возбудятся переменные ЭДС, которые, в свою очередь, создадут переменные индукционные вихревые токи. Магнитное поле этих токов будет замкнутым (рисунок 6, б); внутри цилиндра оно будет направлено навстречу возбуждающему полю, а за его пределами – в ту же сторону, что и возбуждающее поле. Результирующее поле (рисунок 6, в) оказывается ослабленным у цилиндра и усиленным вне его, т. е. происходит вытеснение поля из пространства, занимаемого цилиндром, в чем и заключается его экранирующее действие.
|
38) Распространение электромагнитной волны в диэлектрике
|
39) Векторный и скалярный потенциалы в переменном электромагнитном поле.
|
40) Запаздывающие потенциалы переменного электромагнитного поля
|
|
|
 Скачать 120 Kb.
Скачать 120 Kb.