РАДИАННАЯ МЕРА УГЛА. КР математика радинная. Чпоу скп контрольная работа дисциплина математика Тема радианная мера Пушкарский Д. И. Специальность Информационная безопасность Группа иб 223
 Скачать 90.71 Kb. Скачать 90.71 Kb.
|
|
ЧАСТНОЕ ПРОФЕССИОНАЛЬНОЕ ОБРАЗАВАТЕЛЬНОЕ УЧЕРЕЖДЕНИЕ «СУРГУТСКИЙ КОЛЛЕДЖ ПРЕДПРИНИМАТЕЛЬСТВА» (ЧПОУ «СКП») КОНТРОЛЬНАЯ РАБОТА Дисциплина: математика Тема: радианная мера Выполнил: Пушкарский Д.И. Специальность Информационная безопасность Группа: ИБ 22/3 Зачетная книжка № Проверил – преподаватель ------------------------------------ Дата: «14» ноября 2022 г. Оценка: Сургут, 2022 г. Оглавление Радианная мера угла…………………………………………………………………………3 Таблица градусов в радианах…………………………………………………………..4 Краткая история радиана…………………………………………………………………5 Радианная мера угла Для его измерения рассмотрим единичную окружность, где вершина угла совпадает с его центром. Затем нарисуем дугу, равную радиусу окружности и соединим концы дуги с центром. 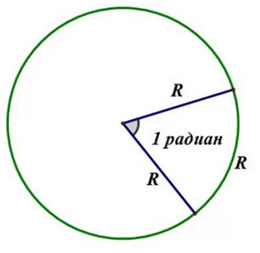 Радиан- угол, соответствующий дуге, длина которой ровна её радиусу. Выразим 1 радиан в градусах. Для этого разделим левую и правую части радиуса на пи. 1 рад=180π° - град. мера угла в 1 радиан равна 180π. Также можно выразить один градус в радианах. Чему равен 1 радиан и во что он будет переходить? Вот простой расчет. 1°=π180рад Можно произвести приблизительные вычисления величин угла в радианах и наоборот. Для этого возьмем значения числа π с точностью до десятитысячных и подставим в полученные формулы. Можно произвести приблизительные вычисления величин угла в радианах и наоборот. Для этого возьмем значения числа π с точностью до десятитысячных и подставим в полученные формулы. 1 рад=180π°=1803,1416°=57,2956° Значит, в одном радиане примерно 57 градусов 1°=π180рад=3,1416180рад=0,0175 рад Один градус содержит 0,0175 радиана. Пример 1. Перевод косинуса угла из радианов в градусы Пусть α=3,2 рад. Нужно узнать градусную меру этого угла. Применим формулу перехода от радианов к градусам и получим: 3,2 рад=3,2·180π°≈3,2·1803,14°≈5763,14°≈183,4° Пример 2. Перевод из градусов в радианы Переведем 47 градусов в радианы. Согласно формуле, умножим 47 на пи и разделим на 180. 47°≈47·3,14180≈0,82 рад Таблица градусов в радианах  Краткая история радиана Слово "радиан" было придумано Томасом Муиром или Джеймсом Томпсоном около 1870 года, математики измеряли углы таким образом в течение длительного времени. Например, Леонард Эйлер (1707-1783) в своих исследованиях в алгебре измерял углы по длине дуги, отрезанной в единичной окружности. Это ему было необходимо для того, чтобы дать его знаменитую формулу с комплексными числами, которая связывает функции косинусов с экспоненциальной функцией. 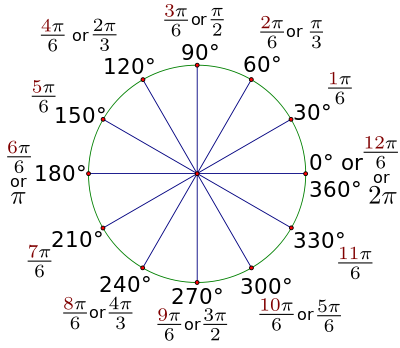 https://myalfaschool.ru/articles/radiannaya-mera-ugla https://zaochnik.com/spravochnik/matematika/trigonometrija/gradusy-i-radiany/ |
