начерт. Что изучает начертательная геометрия

• Название: Что изучает начертательная геометрия
• Дата: 16.01.2019
• Размер: 1.53 Mb.
• Имя файла: начерт .docx
• Тип: Документы; #63928
• страница: 2 из 3

Поворот вокруг оси

Для того, чтобы отрезок стал параллелен плоскости проекции и без искажения отразился на ней, он может быть повернут вокруг проецирующей прямой, проходящей через один из его концов.

Определим длину произвольного отрезка MN. Для этого через точку N проводим горизонтально проецирующую прямую i. Вокруг неё поворачиваем MN так, чтобы его проекция M'N' заняла положение M'₁N'₁, параллельное оси X.

По линиям связи находим точку M''₁. При этом исходим из того, что M'' в процессе вращения движется параллельно горизонтальной плоскости.

Точка N не изменит своего положения, так как лежит на оси поворота. Поэтому осталось только соединить N''₁ и M''₁ искомым отрезком. На рисунке он выделен красным цветом.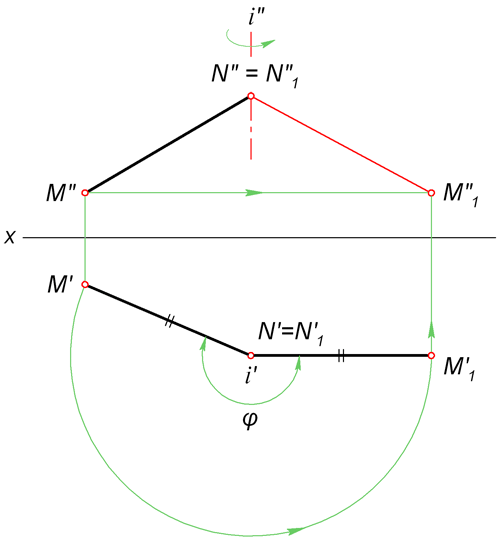



Метод замены плоскостей проекции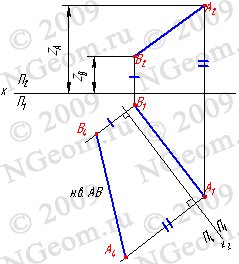


6. Перечислите способы определения натуральной величины угла между двумя пересекающимися прямыми

Чтобы определить натуральную величину угла, нужно перевести его в положение, в котором его стороны будут параллельны плоскости проекции. Наиболее рациональный путь решения данной задачи – использовать способ вращения вокруг линии уровня. Более трудоемкими вариантами являются метод замены плоскостей проекций и параллельное перемещение.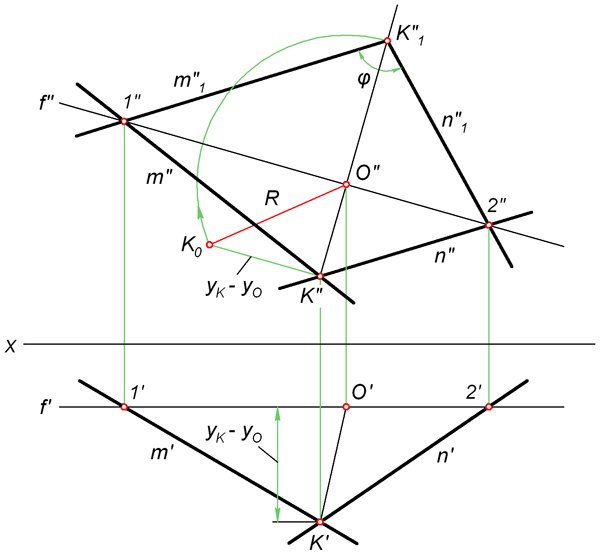



Последовательность построений:

1. 
   В произвольном месте чертежа проводим фронталь f. Она пересекает прямые m и n в точках 1 и 2. Определяем их недостающие проекции.
   
2. 
   Через точку K'' проводим перпендикуляр к f''. На пересечении этого перпендикуляра с фронталью находится проекция центра вращения O''. По линии связи определяем положение т. O'.
   
3. 
   Находим величину радиуса R поворота точки K. Для этого перпендикулярно O''K'' откладываем отрезок K''K₀ = y_k – y_o. Таким образом, R равен O''K₀ – гипотенузе прямоугольного треугольника O''K''K₀.
   
4. 
   Проводим дугу радиусом R до её пересечения с перпендикуляром O''K'' в точке K''₁. Соединяем K''₁ c точками 1'' и 2''. Натуральная величина угла между прямыми m и n равна углу ϕ при вершине K''₁.
   

7. Как определить углы наклона отрезка прямой общего положения к плоскостям проекций? Показать на примере

Углы наклона прямой общего положения по двум ее проекциям находятся попутно при определении действительной величины отрезка способом прямоугольного треугольника. В отличие от отрезков прямых частного положения, проецирующихся хотя бы на одну из плоскостей проекций в натуральную величину, отрезок прямой общего положения на плоскости проекций проецируется с искажением. Для того чтобы найти его натуральную величину, необходимо провести ряд преобразований.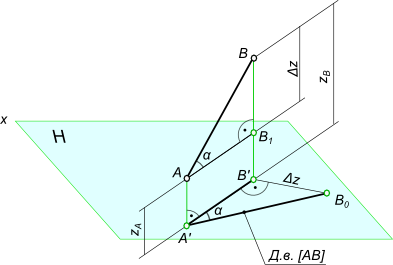



Углы наклона прямой

1.	tg α= BB1/AB1=(BB`−B`B1)/AB1=(zB−zA)/A`B`

Возьмем прямую общего положения АВ и спроецируем ее на горизонтальную плоскость проекций . Через точку А проведем линию, параллельную плоскости . Таким образом в пространстве получим прямоугольный треугольник , один из катетов которого (AB₁) равен длине проекции отрезка, а угол между отрезком и этим катетом является углом наклона заданного отрезка к плоскости проекций (рис.).

Для определения натуральной величины отрезка прямой общего положения и угла наклона ее к плоскости проекций на эпюре (КЧ) необходимо построить прямоугольный треугольник:
- первый катет этого треугольника равен проекции отрезка на плоскости проекций (обычно прямоугольный треугольник пристраивают к проекции отрезка, однако в некоторых задачах целесообразно прямоугольный треугольник строить в стороне от проекций геометрических объектов);
- из проекции любого конца отрезка под прямым углом к проекции отрезка проводится луч, на котором откладывается длина второго катета, равная разности расстояний от концов отрезка до данной плоскости проекций;
- гипотенуза полученного таким образом прямоугольного треугольника равна действительной величине заданного отрезка;
- угол наклона отрезка к той или иной плоскости проекций равен углу между гипотенузой – натуральной величиной и катетом – проекцией на эту плоскость проекций.

Углы наклона прямой, отрезка общего положения всегда будут меньше их ортогональных проекций.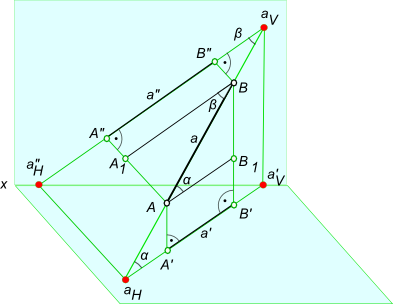



Для графического определения на эпюре Монжа действительной величины отрезка достаточно построить прямоугольный треугольник, взяв за один его катет горизонтальную (фронтальную, профильную) проекцию отрезка, а за другой катет - разность удаления концов отрезка от горизонтальной (или соответственно фронтальной, профильной) плоскости проекции.

2.	tg α= BB1/AB1=(BB`−B`B1)/AB1=(zB−zA)/A`B`
3.	tg β= AA1/BA1=(AA"−A"A1)/BA1=(yA−yB)/A"B"

Графическое определение действительной величины отрезка [AB] путем построения прямоугольных треугольников ΔA`B`B₀ или ΔA"B"A₀ и попутно углов его наклона:
- α к горизонтальной плоскости проекции;
- β к фронтальной плоскости проекции.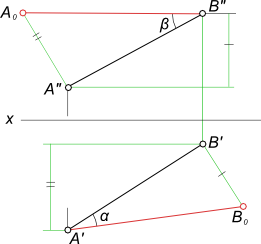



Углы наклона прямой к плоскости проекций проецируется на эпюре без искажений, когда она занимает положение прямой уровня, это может быть:
- Горизонтальная прямая;
- Фронтальная прямая;
- Профильная прямая
8. Какие плоскости называются проецирующими? Перечислите их основные особенности

Одним из частных случаев расположения плоскости является

расположение перпендикулярное к одной из плоскостей проекции;

Плоскости, перпендикулярные к плоскостям проекции, называют проецирующими.

горизонтально-проецирующая плоскость α⊥H;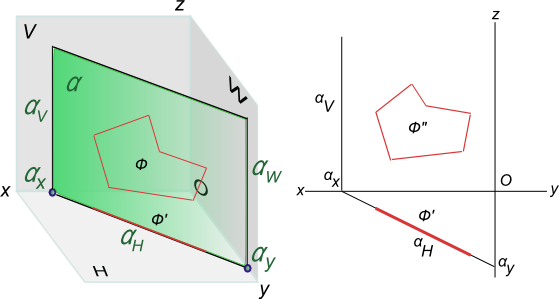



Проецирующая плоскость

фронтально-проецирующая плоскость α⊥V;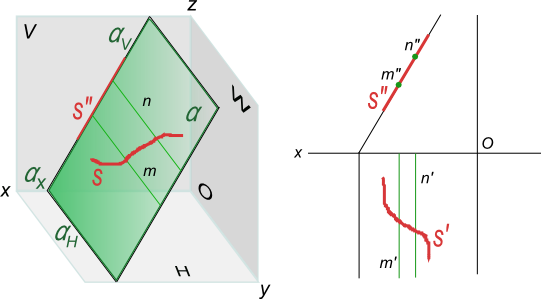



Проецирующая плоскость

профильно-проецирующая плоскость α⊥W;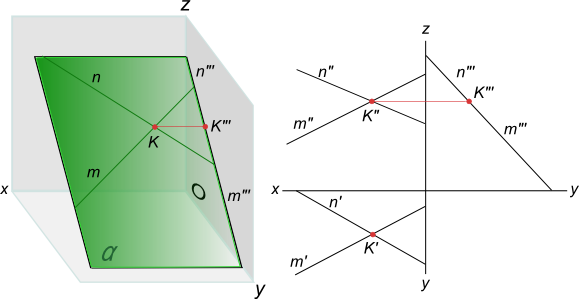



Проецирующая плоскость

Проецирующая плоскость имеет одно важное свойство , заключающееся в том, что проекция точек, а следовательно, и любых геометрических фигур, принадлежащих горизонтально проецирующей плоскости, принадлежат горизонтальному следу этой плоскости.

Аналогичное утверждение справедливо и для фронтально проецирующей и для профильно проецирующей плоскостей.
9. Какие линии называются главными линиями плоскости? Как они строятся на эпюре?

Кроме прямых общего положения в плоскости можно выделить линии частного положения, которые называют главными линиями плоскости – это линии уровня и линии наклона плоскости.

1. Горизонтали плоскости h – прямые, принадлежащие плоскости и параллельные плоскости p₁ (рис. 4.6).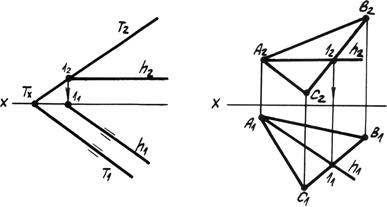

 
Рис. 4.6. Горизонтали плоскости.

На эпюре фронтальная проекция горизонтали h₂ параллельна оси x, а горизонтальная проекция горизонтали h₁параллельна горизонтальному следу плоскости h₁ || Т₁, т.е. горизонтальный след плоскости – это тоже её горизонталь.

2. Фронтали плоскости ¦ – прямые, принадлежащие плоскости и параллельные плоскости p₂ (рис. 4.7).

На эпюре горизонтальная проекция фронтали ¦₁ параллельна оси x₁, а фронтальная проекция фронтали параллельна фронтальному следу плоскости ¦₂ || Г₂, т.е. фронтальный след плоскости – это тоже фронталь плоскости.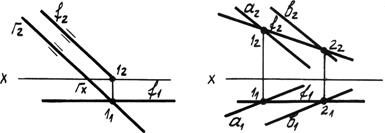

 
Рис. 4.7. Фронтали плоскости.

3. Профильные прямые плоскости p – прямые, принадлежащие плоскости и параллельные плоскости p₃ (рис. 4.8).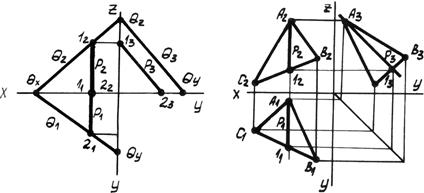

 
Рис. 4.8. Профильные прямые плоскости.

На эпюре горизонтальная и фронтальная проекции профильной прямой р₁ и р₂ перпендикулярны оси x, а профильная проекция профильной прямой р₃ параллельна профильному следу р₃ || q₃, т.е. профильный след плоскости – это тоже её профильная прямая.

10. Что такое линия наибольшего ската плоскости? Следы и точки схода следов плоскости

Линия наибольшего наклона плоскости l – это прямая, принадлежащая плоскости и перпендикулярная к соответствующей линии уровня плоскости. С  помощью линии наибольшего наклона определяется угол наибольшего наклона плоскости к соответствующей плоскости проекции.

Линия l, перпендикулярная горизонтальной плоскости, определяет угол наклона плоскости к плоскости p₁ (рис. 4.9).

Если плоскость задана следами, то горизонтальная проекция линии наибольшего наклона плоскости перпендикулярна горизонтальному следу l₁ (рис. 4.9). Если плоскость задана другим способом, необходимо построить горизонталь плоскости, тогда горизонтальная проекция линии наибольшего наклона определяется перпендикулярно горизонтальной проекции горизонтали, l₁ ^ h₁.

Аналогично можно построить линии наибольшего наклона к другим плоскостям проекции.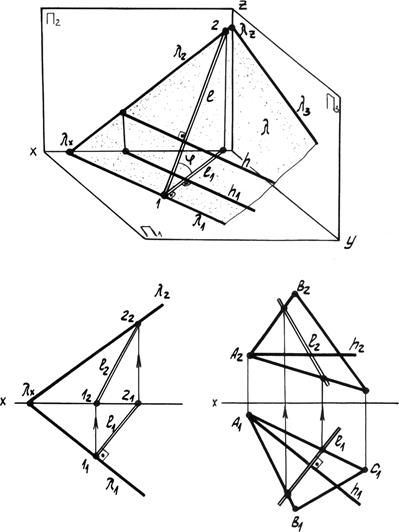

 
Рис. 4.9. Линия наибольшего наклона плоскости.


След плоскости Р – это линия пересечения ее с данной плоскостью или поверхностью (рис. 36).

Линию пересечения плоскости Р с горизонтальной плоскостью называют горизонтальным следом и обозначают P_h, а линию пересечения с фронтальной плоскостью – фронтальным следом и обозначают Р_v (рис. 37).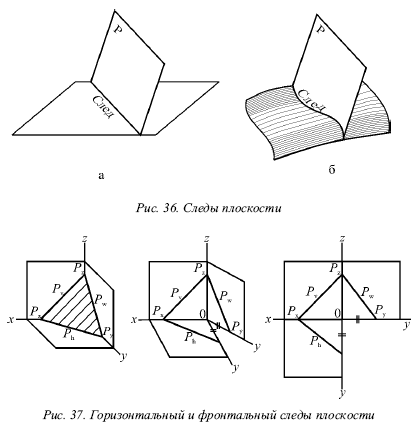



Иногда применяется и профильный след P_w – линия пересечения данной плоскости с профильной плоскостью.

Точки, в которых пересекается плоскость Р с осями проекций, называют точками схода следов. Р_х – точка схода следов на оси х, P_у – на оси у, а Р_z – на оси z (рис. 37). в точке Р пересекаются следы P_h и P_v и т. д.

Следы P_h и P_v плоскости Р являются прямыми, которые и лежат на горизонтальной и фронтальной плоскостях. Они имеют по одной из своих проекций, которые совпадают с осью х: горизонтальный след P_h – фронтальную, а фронтальный P_v– горизонтальную проекции.

Любую плоскость Р можно задать на эпюре с помощью указания положения двух ее следов – горизонтального и фронтального (рис. 38).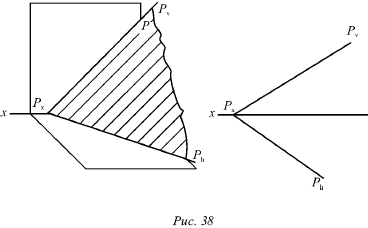



Следы P_h и P_v чаще всего изображаются парой пересекающихся или параллельных прямых и поэтому могут определять положение плоскости в пространстве.

Построение следов плоскости

Построение следов плоскости бывает необходимо, когда плоскость задана прямыми, точкой и прямой и тремя точками.
Построение следов плоскости производят из условия: если прямая общего положения лежит в плоскости, то ее следы лежат на одноименных следах этой плоскости.
Построение следов плоскости α, заданной двумя пересекающимися прямыми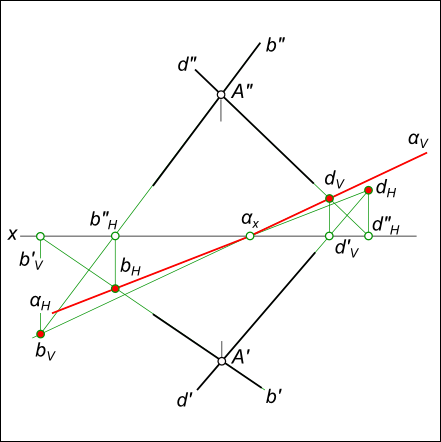



Построение следов плоскости

выполняют исходя из того что следы плоскости - это пересекающиеся прямые. Для проведения каждого следа на эпюре необходимы две точки:
- для горизонтального следа αH найдены bH и dH, горизонтальные следы прямых b и d соответственно;
- для фронтального следа αV найдены dV и αx, фронтальный след прямой d и точка схода следов соответственно.

Построение следов плоскости α, заданной двумя параллельными прямыми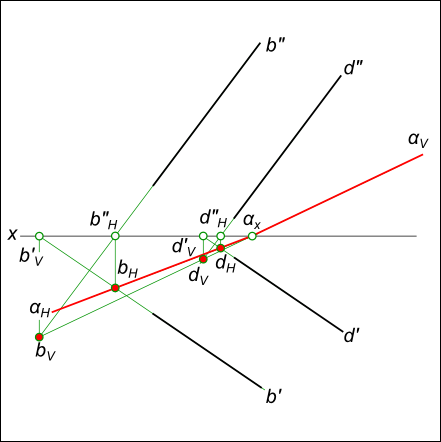



Построение следов плоскости

Для проведения каждого следа на эпюре необходимы две точки:
- для горизонтального следа αH найдены bH и dH, горизонтальные следы прямых b и d соответственно;
- для фронтального следа αV найдены bV и αx, фронтальный след прямой d и точка схода следов соответственно.

Построение следов плоскости α, заданной пересекающимися горизонталью и фронталью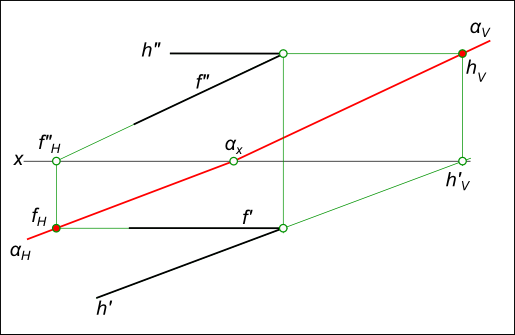



Построение следов плоскости

Для проведения каждого следа на эпюре необходима одна точка:
- для горизонтального следа αH найдены fH ;
- для фронтального следа αV могут быть использованы hV или αx, фронтальный след прямой h или точка схода следов соответственно.

Если требуется выполнить построение следов плоскости, заданной тремя точками, тогда следует соединить одноименные проекции точек прямыми линиями, которые или пересекаются или параллельны между собой . Дальнейший ход решения показан в выше изложенных примерах.

Построение следов плоскости заданной одним из следов и точкой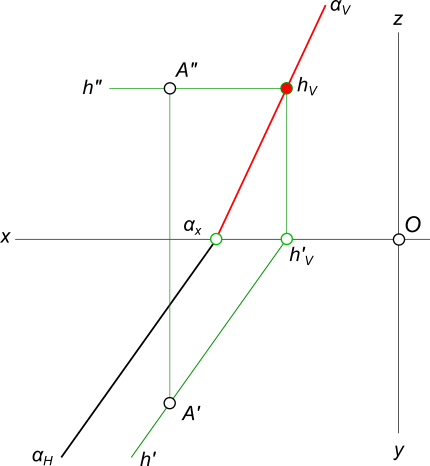



Построение следов плоскости

Через точку A проводим горизонталь h плоскости и находим ее след hV.
Проводим фронтальный след плоскости α через след прямой hV и точку схода следов αx.

или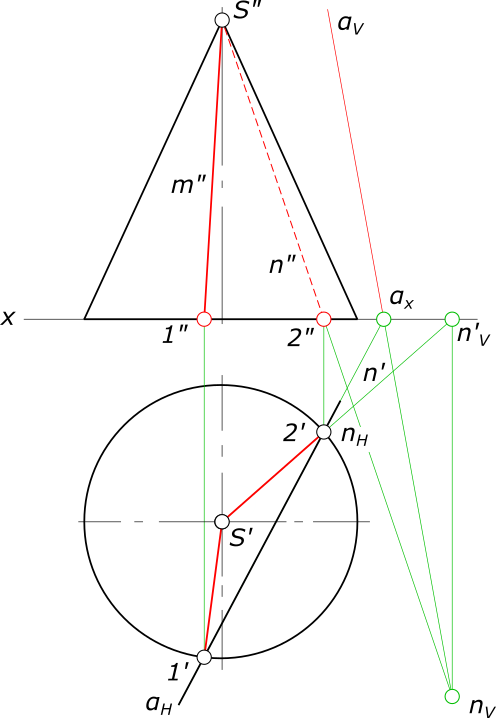



Построение следов плоскости

Построение следов плоскости бывает необходимо, из условия принадлежности точки или прямой плоскости.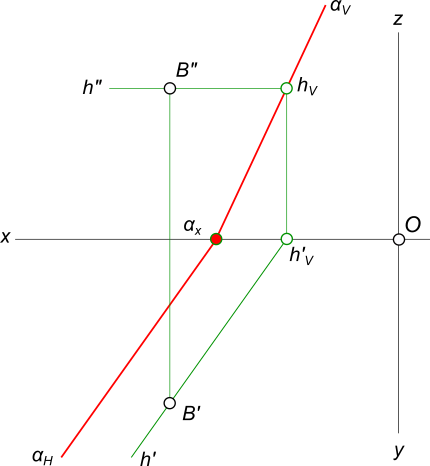



Построение следов плоскости

Через точку B проводим произвольную прямую h - горизонталь плоскости и находим ее след hV.
Проводим фронтальный след αV через след hV произвольного направления. Проводим горизонтальный след αH через точку схода следов αx.


8) Какие плоскости называются проецирующими? Перечислите их основные особенности.

Плоскости перпендикулярные перпендикулярные к плоскостям проекции, называются проецирующими.

Проецирующая плоскость имеет одно важное свойство , заключающееся в том, что проекция точек, а следовательно, и любых геометрических фигур, принадлежащих горизонтально проецирующей плоскости, принадлежат горизонтальному следу этой плоскости.
10) Линия наибольшего ската плоскости? Следы и точки схода следов плоскости?

Это прямая, принадлежащая плоскости и перпендикулярная одной из линий уровня плоскости. С её помощью определяют угол наклона заданной плоскости к одной из плоскостей проекций.

Следом плоскости называется линия пересечения плоскости с плоскостью проекций. В зависимости, от того с какой из плоскостей проекций пересекается данная плоскость, различают: горизонтальный, фронтальный и профильный следы плоскости. Каждый след плоскости является прямой линией, для построения которых необходимо знать две точки, либо одну точку и направление прямой.

Точки пересечения плоскости α с координатными осями X, Y, Z называются точками схода следов и обозначаются соответственно S_x, S_y, S_z

11)Как в плоскости строится точка?

Как построить на чертеже точку, лежащую в заданной плоскости? Для того чтобы сделать это, предварительно строят прямую, лежащую в заданной плоскости, и на этой прямой берут точку.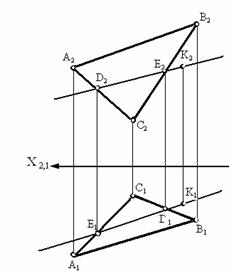




Например, требуется найти фронтальную проекцию точки D, если задана ее горизонтальная проекция D' и известно, что точка D должна лежать в плоскости, определяемой треугольником АВС (рис. 110).

Сначала строят горизонтальную проекцию некоторой прямой так, чтобы точка D могла оказаться на этой прямой, а последняя была бы расположена в данной плоскости. Для этого проводят прямую через точки А' и D' и отмечают точку М', в которой прямая A'D' пересекает отрезок В'С'. Построив фронтальную проекцию М" на В"С", получают прямую AM, расположенную в данной плоскости: эта прямая проходит через точки А и М, из которых первая заведомо принадлежит данной плоскости, а вторая в ней построена.

Искомая фронтальная проекция D" точки D должна быть на фронтальной проекции прямой AM.

Другой пример дан на рис. 111. В пл. β, заданной параллельными прямыми АВ и CD, должна находиться точка К, для которой дана лишь горизонтальная проекция — точка К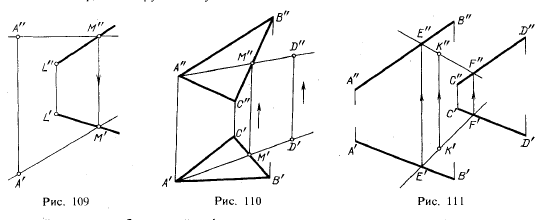

Через точку К' проведена некоторая прямая, принимаемая в качестве горизонтальной проекции прямой в данной плоскости. По точкам E' и F' строим Е" на А"В" и F" на C"D". Построенная прямая EF принадлежит пл. β, так как проходит через точки Е и F, заведомо принадлежащие плоскости. Если взять точку К" на E"F", го точка К окажется в пл.β

12) Когда прямая параллельна плоскости

Прямая параллельна плоскости, если она параллельна прямой b, принадлежащей этой плоскости.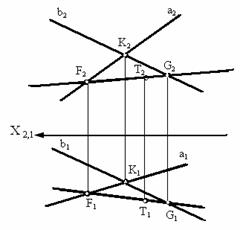

Прямые, параллельные плоскостям, заданным:


а – плоскостью треугольника АВС;
б – двумя пересекающимися прямыми а∩b;

в – горизонтальным h0α и фронтальным f0α следами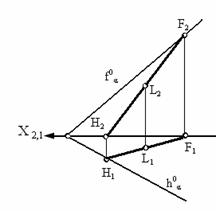



К числу прямых, занимающих особое положение в плоскости, отнесем горизонтали, фронтали

Горизонталями плоскости называются прямые, лежащие в пей и параллельные горизонтальной плоскости проекций.

Фронталями плоскости называются прямые, лежащие в ней и параллельные плоскости проекций π2.
Построение прямой, параллельной заданной плоскости, основано на следующем положении, известном из геометрии: прямая параллельна плоскости,если эта прямая параллельна любой прямой в плоскости.

Через заданную точку в пространстве можно провести бесчисленноемножество прямых линий, параллельных заданной плоскости: Для полученияединственного решения требуется какое-нибудь дополнительное условие.
Например, через точку (рис. 180) требуется провести прямую,

параллельную плоскости, заданной треугольником ABC, и плоскости проекций !

(дополнительное условие).

Очевидно, искомая прямая должна быть параллельна линии пересечения

обеих плоскостей, т.е. должна быть параллельна горизонтальному следу

плоскости, заданной треугольником ABC. Для определения направления этого следа можно воспользоваться горизонталью плоскости, заданной треугольником

ABC. На рис. 180 проведена горизонталь DC и затем через точку M проведена

прямая, параллельная этой горизонтали.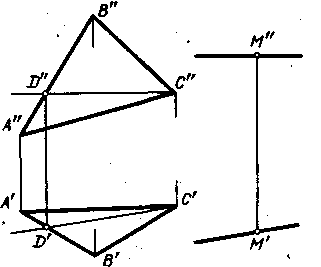

Поставим обратную задачу: через заданную точку провести плоскость,

параллельную заданной прямой линии. Плоскости, проходящие через некоторую

точку А параллельно некоторой прямой ВС, образуют пучок плоскостей, осью

которого является прямая, проходящая через точку А параллельно прямой ВС.

Для получения единственного решения требуется какое-либо дополнительное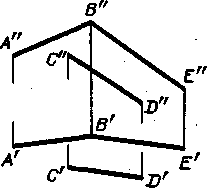

условие.


72


Например, надо провести плоскость, параллельную прямой CD, не через

точку, а через прямую АВ (рис. 181). Прямые АВ и CD - скрещивающиеся. Если

через одну из двух скрещивающихся прямых требуется провести плоскость,

параллель-

ную другой, то задача имеет единственное решение. Через точку В

проведена прямая, параллельная прямой CD; прямые АВ и BE определяют

плоскость, параллельную прямой CD.
Как установить, параллельна ли данная прямая данной плоскости?

Можно попытаться провести в этой плоскости некоторую прямую параллельно данной прямой. Если такую прямую в плоскости не удается построить, то заданные прямая и плоскость не параллельны между собой.

Можно попытаться найти также точку пересечения данной прямой с данной плоскостью. Если такая точка не может быть найдена,, то заданные прямая и плоскость взаимно параллельны.
13)Как строится прямая перпендикулярная плоскости?

Из всех возможных положений прямой, пересекающей плоскость, отметим

случай, когда прямая перпендикулярна к плоскости, и рассмотрим свойства

проекций такой прямой.

На рис. 185 задана плоскость, определяемая двумя пересекающимися
прямыми AN и AM, причем AN является горизонталью, a AM -- фронталью этой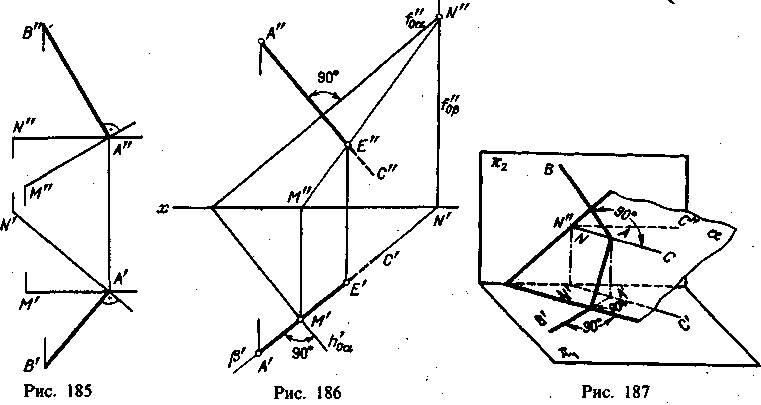

плоскости. Прямая АВ, изображенная на том же чертеже, перпендикулярна к AN и к AM и, следовательно, перпендикулярна к определяемой ими плоскости.

Перпендикуляр к плоскости перпендикулярен к любой прямой, проведенной в

этой плоскости. Но чтобы при этом проекция перпендикуляра к плоскости общего

положения оказалась перпендикулярной к одноименной проекции какой-либо

прямой этой плоскости, прямая должна быть горизонталью, или фронталью, или

профильной прямой плоскости. Поэтому, желая построить перпендикуляр к

плоскости, берут в общем случае две такие прямые (например, горизонталь и

фронталь, как это показано на рис. 185).

Итак, у перпендикуляра к плоскости его горизонтальная проекция

перпендикулярна к горизонтальной проекции горизонтали, фронтальная проекция

перпендикулярна к фронтальной проекции фронтали, профильная проекция

перпендикулярна к профильной проекции профильной прямой этой плоскости.

Очевидно, в случае, когда плоскость выражена следами (рис. 186), мы

получаем следующий вывод: если прямая перпендикулярна к плоскости, то

горизонтальная проекция этой прямой перпендикулярна к горизонтальному следу

плоскости, а фронтальная проекция перпендикулярна к фронтальному

следу плоскости.

Итак, если в p1, p2 горизонтальная проекция прямой

перпендикулярна к горизонтальному следу и фронтальная проекция прямой

перпендикулярна к фронтальному следу плоскости, то в случае плоскостей

общего положения (рис. 186), а также горизонталъно-и фронтально-проецирующих

прямая перпендикулярна к плоскости. Но для профильно-проецирующей плоскости

может оказаться, что прямая к этой плоскости не перпендикулярна, хотя

проекции прямой соответственно перпендикулярны к горизонтальному и

фронтальному следам плоскости. Поэтому в случае профильно-проецирующей

плоскости надо рассмотреть также взаимное положение профильной проекции

прямой и профильного следа данной плоскости и лишь после этого установить,

будут ли перпендикулярны между собой данные прямая и плоскость.

Очевидно (рис. 187), горизонтальная проекция перпендикуляра к плоскости

сливается с горизонтальной проекцией линии ската, проведенной в плоскости

через основание перпендикуляра.

На рис. 186 из точки А проведен перпендикуляр к пл. (А"С" перпендикулярно f"o, AC перпендикулярно h'o) и показано построение точки Е, в которой перпендикуляр АС пересекает

пл. . Построение выполнено с помощью горизонтально-проецирующей пл. ,

проведенной через перпендикуляр АЕ.

На рис. 188 показано построение перпендикуляра к плоскости,

определяемой треугольником ABC. Перпендикуляр'проведен через точку А.

Так как фронтальная проекция перпендикуляра к плоскости должна быть

перпендикулярна к фронтальной проекции фронтали плоскости, а его

горизонтальная проекция перпендикулярна к горизонтальной проекции

горизонтали, то в плоскости через точку А проведены фронталь с проекциями

A'D' и A"D" и горизонталь А"Е", А'Е'. Конечно, эти прямые не обязательно

проводить именно через точку А.

Далее проведены проекции перпендикуляра: M"N"% A"D", M'N'% A'E'. Почему

проекции на рис. 188 на участках A"N" и А'М' показаны штриховыми линиями?

Потому, что здесь рассматривается плоскость, заданная треугольником ABC, а

не только этот треугольник: перпендикуляр находится частично перед

плоскостью, частично за ней.

На рис. 189 и 190 показано построение плоскости, проходящей через точку

А перпендикулярно к прямой ВС. На рис. 189 плоскость выражена следами.

Построение начато с проведения через точку А горизонтали искомой плоскости:

так как горизонтальный след плоскости должен быть перпендикулярен к В'С, то

и горизонтальная проекция горизонтали должна быть перпендикулярна к В'С.

Поэтому A'N'% В'С'. Проекция A"N" \\ оси х, как это должно быть у

горизонтали. Затем проведен через точку " (" - фронтальная проекция

фронтального следа горюонтали AN) след f"o% В"С", получена точка X, и

проведен след h'o" II-4'-V' (h^LB'C).

На рис. 190 плоскость определена ее фронталью AM и горизонталью AN. Эти

прямые перпендикулярны к ВС (А"М"% В"С", A'N' %

В'С); определяемая ими плоскость перпендикулярна к ВС.

Так как перпендикуляр к плоскости перпендикулярен к каждой прямой,

проведенной в этой плоскости, то, научившись проводить плоскость

перпендикулярно к прямой, можно воспользоваться этим для проведения

перпендикуляра из некоторой точки А к прямой общего положения ВС. Очевидно,

можно наметить следующий план построения проекций искомой прямой:

1) через точку А провести плоскость (назовем ее ), перпендикулярную к

ВС;

2) определить точку К пересечения прямой ВС с ил. ;

соединить точки А и К отрезком прямой линии.

Прямые АК и ВС взаимно перпендикулярны.

Пример построения дан на рис. 191. Через точку А проведена плоскость

(), перпендикулярная к ВС. Это сделано при помощи фронтали, фронтальная

проекция

A"F" которой проведена перпендикулярно к фронтальной проекции В"С", и

горизонтали, горизонтальная проекция которой перпендикулярна к В'С.

Затем найдена точка К, в которой прямая ВС пересекает пл. . Для этого

через прямую ВС проведена горизонтально-проецирующая плоскость (на чертеже

она задана только горизонтальным следом 1). Пл. пересекает пл.

по прямой с проекциями 1'2' и 1 "2". В пересечении этой прямой с прямой ВС

получается точка К. Прямая АК является искомым перпендикуляром к ВС.

Действительно, прямая АК пересекает прямую ВС и находится в пл. ,

перпендикулярной к прямой ВС', следовательно, AKLBC.

14)Как в общем случае строится линия пересечения двух плоскостей ; прямойи плоскости?

в общем случае для построения линии пересечения двух

плоскостей надо найти какие-либо две точки, каждая из которых принадлежит обеим плоскостям; эти точки определяют линию пересечения плоскостей.

Общий случай построения линии пересечения двух плоскостей. Пусть одна из плоскостей, β, задана двумя пересекающимися прямыми, а другая, γ,— двумя параллельными прямыми. Построение показано на рис. 166. В результате взаимного пересечения плоскостей β и γ получена прямая K1K2. Выразим это записью: β × γ = К1K2.

Для определения положения точек K1 и К2 возьмем две вспомогательные фронтально-проецирующие плоскости (α1, и α2), пересекающие каждую из плоскостей β и γ. При пересечении плоскостей β и γ плоскостью α1. получаем прямые с проекциями 1"2", 1'2' и 3"4", 3'4'. Эти прямые, расположенные в пл. α1, в своем пересечении определяют первую точку, К1, линии пересечения плоскостей β и γ.

Введя, далее, ил. α2, получаем в ее пересечении с β и γ прямые с проекциями 5"6", 5'6' и 7"8", 7'8'. Эти прямые, расположенные в пл. α2, в своем пересечении определяют вторую точку, К2, общую для β и γ.

Получив проекции К'1 и К'2 находим на следах и α"1 и α"2 проекции К"1 и К"2. Этим определяются проекции К'1К'2 и К"1К"2 искомой прямой пересечения плоскостей β и γ(проекции проведены штрихпунктирной линией).




Для построения точки пересечения прямой с плоскостью общего положения

надо выполнить следующее (рис. 158):

1) через данную прямую (АВ) провести некоторую вспомогательную

плоскость (α),

2) построить прямую (MN) пересечения плоскости данной (β) и

вспомогательной (α),

3) определить положение точки (К) пересечения прямых -- данной (АВ) и

построенной (MN).

На рис. 172 показано построение точки пересечения прямой FK с

плоскостью общего положения, заданной двумя пересекающимися прямыми АВ и CD,

Через прямую FK проведена вспомогательная фронтально-проецирующая

плоскость . Выбор фронтально-проецирующей плоскости объясняется удобством

построения точек пересечения ее фронтального следа с проекциями А"В" и

С"D". По точкам М" и " найдены горизонтальные проекции М' и N' и

тем самым определена прямая , по которой

вспомогательная пл. пересекает

данную пл. . Затем найдена точка К', в которой горизонтальная проекция

прямой непосредственно или

при своем продолжении пересекает проекцию M'N'. После этого остается

найти фронтальную проекцию точки пересечения -- точку К".

На рис. 173 показано построение точки пересечения прямой MN с

плоскостью, заданной треугольником ABC. Ход построения не отличается от

рассмотренного на рис. 172. Но вспомогательная (на этот раз

горизонтально-проецирующая) плоскость в данном .случае указана только одним

следом ', проходящим через проекцию M'N'. Пл. γ пересекает ABC no прямой

DE. Но можно обойтись и без γ ': мысленно представляя себе

вспомогательную.горизонтально-проецирующую плоскость, проходящую через MN ,

выражаем проекциями E'D' и E"D" отрезок ED, по которому проведенная через MN

горизонтально-проецирующая плоскость пересекает треугольник.

Считая, что в пространстве заданы прямая и непрозрачный треугольник,

определим видимые и невидимые части прямой MN относительно плоскостей p1 и pw

В точке E' на пл. p1 совмещаются горизонтальные проекции двух точек, из

которых одна принадлежит прямой MN (фронтальная проекция E"1), а другая --

стороне треугольника А С (фронтальная проекция E").

Из расположения фронтальных проекций Е'1 и Е" следует, что на участке

КМ прямая находится над треугольником и, следовательно, на горизонтальной

проекции отрезок М'К' -- весь видимый, а отрезок K'D' -- невидимый.

На фронтальной проекции в точке F" совмещаются фронтальные проекции

двух точек, из которых одна принадлежит прямой MN, а другая -- стороне

треугольника АВ. По расположению горизонтальных проекций F' и F( заключаем,

что прямая MN на участке К находится за треугольником и, следовательно, на

фронтальной проекции отрезок F"K" -- невидимый, а отрезок K"N" -- видимый.

15)Как строится линия пересечения плоскостей, заданных следами?

На рис. 174-- 176 даны примеры построения точки пересечения прямой с

плоскостью общего положения, выраженной следами. В первом примере через

прямую AB проведена горизонтально-проецирующая пл. , а во втором (рис. 175)

-- горизонтальная плоскость, что оказалось 'возможным сделать, так как в

этом примере прямая AB -- горизонтальная.


Изображенная на рис. 176 прямая перпендикулярна к пл. ,.

Горизонтальные проекции всех точек

этой прямой сливатся в одну точку.

Следовательно, положение проекции К' искомой точки пересечения прямой AB с

пл. известно. Положение проекции К" определено при помощи горизонтали.
16)Для чего используются преобразование проекций? Какие способы преобразования проекций вы знаете?

Преобразование проекций используется для наиболее выгодного изображения геометрических фигур при их исследовании и для решения метрических и позиционных задач. После преобразования чертежа объекты занимают частное положение относительно плоскостей проекций. Существует несколько способов преобразования проекций:
- способ замены плоскостей проекций;
- способ вращения вокруг проецирующих прямых и прямых уровня;
- способ плоскопараллельного перемещения.
Принципиальное отличие первого способа (замены плоскостей проекций) от других заключается в том, что объект не меняет своего положения в пространстве, а вводятся новые дополнительные плоскости проекций. При использовании способов вращения и плоскопараллельного перемещения система плоскостей остаётся неизменной, а объект перемещается относительно системы плоскостей.