начерт. Что изучает начертательная геометрия
 Скачать 1.53 Mb. Скачать 1.53 Mb.
|
|
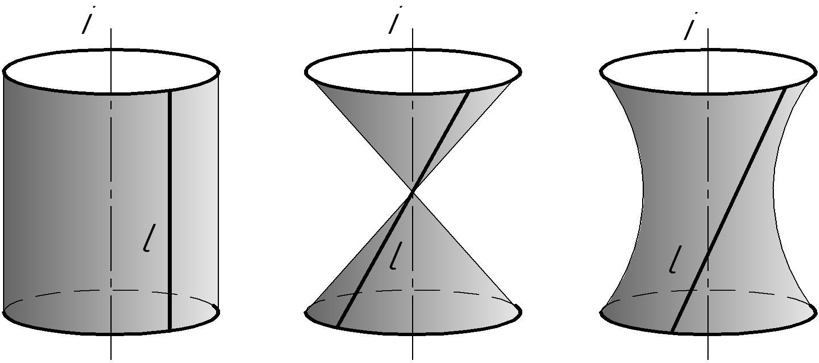
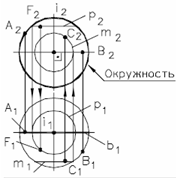
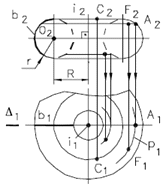
17) В чем заключается способ замены плоскостей проекций? Этот способ заключается в том, что заданную систему плос костей проек ций заменяют новой системой так, что предмет (прямая или плоскость), не изменяя своего положения в про странстве, оказывается в частном положении относительно новой системы плоскостей проекций. Плоскости проекций обра зуют новую ортогональную систему. В зависимости от условий задачи приходится заменять либо одну из заданных плоскостей проекций, либо обе, если заменой одной плоскости проекций не удается получить необходимого расположения проецируемого предмета относительно плоско сти проекций. (стр.11 в рабочке) 18) В чем заключается способ вращения? Сущность способа вращения заключается в том, что заданные точка, линия или плоская фигура вращаются вокруг оси, перпендикулярной к одной из плоскостей проекций, до требуемого положения относительно какой-либо плоскости проекций. Если вращается фигура или тело, то каждая их точка будет перемещаться по окружности. В качестве осей вращения удобнее всего выбирать проецирующие прямые или прямые уровня, тогда точки будут вращаться в плоскостях, параллельных или перпендикулярных плоскостям проекций. Пример: На рис. 232, а ось вращения I проведена через точку А перпендикулярно плоскости Н. При вращении точка В отрезка АВ описала дугу окружности с центром в точке, которая проецируется на плоскость Н в точку а, в эту же точку проеци руется ось I(i). Траектория точки В на плос кость Н спроецировалась без искажения, а ее фронтальная проекция совпала с осью Ох. так как точка В лежит в плоскости Н. Движение точки В остановлено в тот момент, когда го ризонтальная проекция ab отрезка АВ стала параллельной оси Ох. Отрезок расположился параллельно плоскости V и проецируется на нее в натуральную величину. На рис. 232, б ось вращения проведена пер пендикулярно плоскости V через точку С. Ее фронтальная проекция совпала с фронтальной проекцией с' точки С и проекцией оси враще ния I (i') точки D. Фронтальная проекция c'd׳ отрезка CD повернута до положения, параллельного оси Ох. Отрезок стал парал лельным плоскости Н и спроецировался на нее в натуральную величину. Траектория точки D при вращении проецируется на плоскость И отрезком dd\yпараллельным оси Ох. 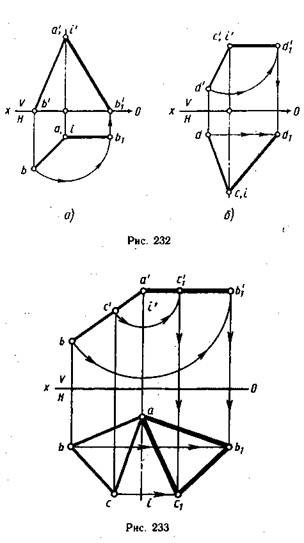 19) В чем заключается способ совмещения? 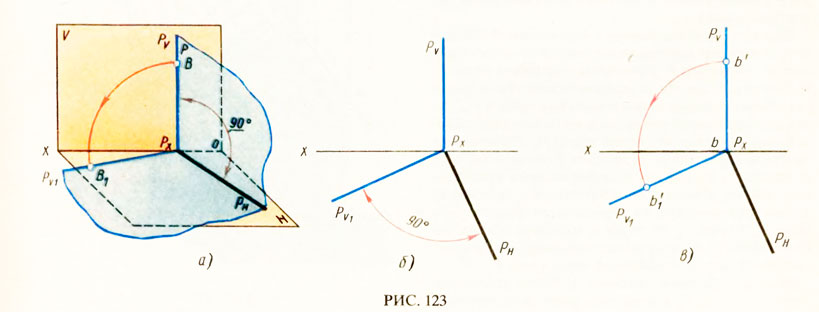 Сущность способа совмещения заключается в том, что плоскость, заданную следами, вращают вокруг одного из следов этой плоскости до совмещения с соответствующей плоскостью проекций, например, вокруг следа Рн до совмещения с горизонтальной плоскостью проекций. Изображения отрезка прямой или плоской фигуры, лежащей в заданной плоскости Р, получаются без искажения. (стр. 12 в рабочке) 20) Что такое определитель поверхности? Определителем поверхности называют совокупность условий, задающих поверхность. Поверхность считается заданной, если относительно любой точки пространства можно однозначно решить вопрос о ее принадлежности данной поверхности. Определитель поверхности состоит из двух частей: геометрической и алгоритмической. В геометрическую часть определителя входят геометрические образы и параметры постоянной формы, положения и величины. 21) По каким основным признакам производится классификация поверхностей? Поверхности классифицируются по многим признакам. Некоторые из них: 1) Кривизна: каждому направлению поверхности от заданной точки соответствует своя форма сечения, которая и определяет кривизну; 2) Наличие касательной к поверхности: обычно касательная к поверхности - это плоскость. В некоторых случая через одну точку поверхности можно провести сколь угодно много касательных. Наличие касательной у какой-либо поверхности влияет на ее гладкость; 3) Метрика и внутренняя геометрия; 4) Нормаль: за нормаль к поверхности принимают единичный вектор, перпендикулярный касательной плоскости в заданной точке. Существует так же нормальное сечение; 5) Геодезические линии: кривая на поверхности называется геодезической линией, если во всех её точках главная нормаль к кривой совпадает с нормалью к поверхности; 6) Площадь: площадь в общем смысле - это числовая характеристика. Существуют поверхности с бесконечной площадью, например параболоид; 7) Ориентация: ориентированной называется двусторонняя поверхность с выбранным направлением нормали. 22. Какие поверхности называются линейчатыми? Линейчатой поверхностью называется поверхность, образованная при перемещении прямой линии в пространстве по какому-либо закону. Характер движения прямолинейной образующей определяет вид линейчатой поверхности. Обычно закон движения образующей задаётся с помощью направляющих линий. Линейчатые поверхности образуются непрерывным движением прямой по некоторой направляющей (прямая, ломаная или кривая линия). Рассмотрим поверхности, образованные движением образующей, один конец которой проходит через неподвижную т-ку S, а второй - перемещается по направляющей m. Определительтакой поверхности имеет вид: Σ (S, m), где S – конечная точка, m – направляющая. Поверхности, образующиеся в данной группе: а) коническая поверхность, где направляющая – кривая, образуется движением прямолинœейной образующей ℓ, скользящей по ней m и проходящей во всœех своих положениях через одну фиксированную т-ку S (не лежащую на криволинœейной направляющей), называемую вершиной конической поверхности. 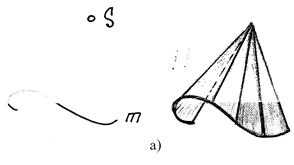 S – конечная точка m – кривая линия частный случай: конус, где m - окружность б) пирамидальная поверхность образуется движением прямолинœейной образующей ℓ по ломаной направляющей m и проходящей через фиксированную т-ку (вершину) S. 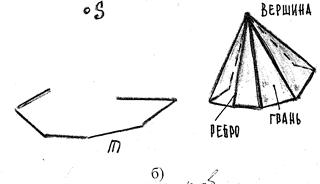 S S – конечная точка; M m – ломаная линия частный случай: пирамида, где m – правильный многоугольник в) цилиндрическая поверхностьобразуется движением прямой ℓ, имеющей постоянное направление ↑ , S бесконечно удалена, ᴛ.ᴇ. всœе образующие двигаются относительно друг-друга параллельно. 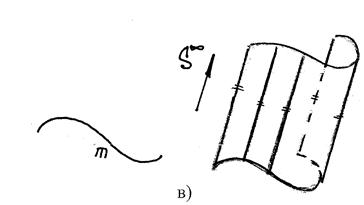 S∞–бескон.удаленная точка S∞–бескон.удаленная точкаm – кривая линия частный случай: цилиндр, где m – окружность, i – ось вращения г) призматическая поверхность образуется движением прямолинœейной образуюей по некоторой ломаной направляющей, при этом S бесконечно удалена. S∞ – бесконечно удаленная точка m – ломаная линия Рис.32. частный случай: призма, где m - ломаная 23. Какие поверхности называются развертываемыми? Поясните на примерах Развертывание поверхности - преобразование поверхности, при котором она совмещается с плоскостью без разрывов и складок. Развертка - плоская фигура, в которую преобразуется поверхность путем совмещения с плоскостью без разрывов и складок. При этом поверхность рассматривают как гибкую, нерастяжимую пленку. Поверхность называется развертываемой на плоскость, если между точками поверхности и плоскости можно установить взаимно однозначное соответствие, при котором: - каждой точке поверхности соответствует точка на развертке; - длины соответствующих линий на поверхности и на развертке равны между собой; - замкнутая линия на поверхности и соответствующая ей линия на развертке ограничивают одинаковую площадь; - угол между линиями на поверхности равен углу между соответствующими им линиям на развертке; - отрезку прямой линии на развертке соответствует геодезическая линия поверхности, кратчайшим путем соединяющая две точки на данной поверхности (рис.1). 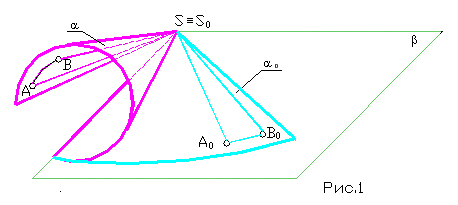 К развертываемым поверхностям относят поверхности: - многогранников; -линейчатые поверхности с параллельными или пересекающимися образующими, а именно - цилиндрические, конические и поверхности с ребром возврата. Развертки многогранников относят к точным разверткам. Развертки линейчатых развертываемых поверхностей выполняют как приближенные. Развертки неразвертываемых поверхностей выполняют условно. 24.Какие поверхности называются поверхностями вращения? Каковы их основные свойства? Поверхность вращения - это поверхность, образованная вращением некоторой линии, называемой образующей поверхности, вокруг неподвижной прямой - оси вращения. При этом образующая, вращаясь вокруг оси, пересекает окружность, называемую направляющей поверхности. Образующей поверхности вращения может быть прямая или кривая линия. В зависимости от этого различают соответственно поверхности вращения линейчатые и криволинейные. К линейчатым поверхностям вращения относятся цилиндр и конус. К криволинейным поверхностям вращения относятся: - сфера (образующая окружность); - эллипсоид (образующая эллипс); - одно и двуполостные гиперболоиды (образующая гипербола); - параболоид (образующая парабола); - торовые (образующая окружность). Все названные виды поверхностей вращения, кроме торовых, являются поверхностями второго порядка (по порядку образующей или направляющей). Торовые поверхности вращения относятся к поверхностям четвертого порядка (по произведению порядков двух окружностей - образующей и направляющей). 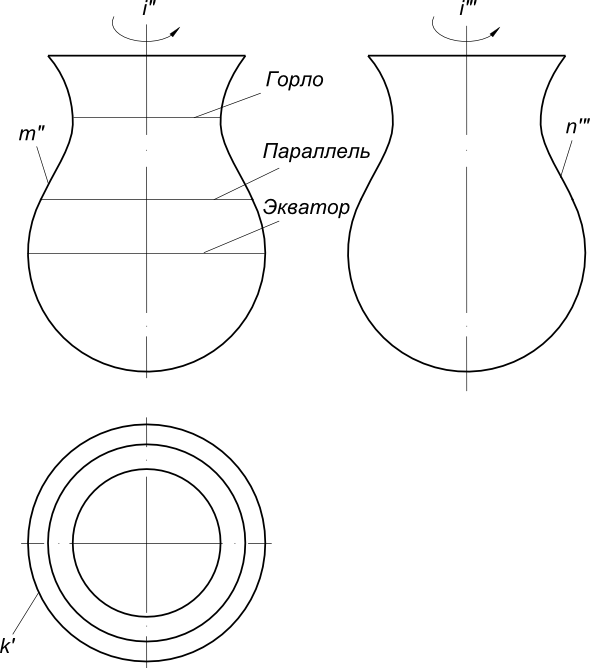 Поверхность вращения На рисунке изображена поверхность вращения общего вида, образующая которой кривая линия вращается вокруг горизонтально-проецирующей оси i. Все точки образующей вращаются вокруг оси i по окружностям соответствующего радиуса, называемыми параллелями поверхности. На фронтальную и профильную плоскости проекций эти параллели проецируются в прямые линии, перпендикулярные оси вращения i. На горизонтальную плоскость проекций параллели проецируются в виде окружностей. Некоторые параллели получили характерные наименования: горло - это параллель наименьшего радиуса; экватор - это параллель наибольшего радиуса. Проекции поверхности вращения образуются следующим образом: - горизонтальная проекция или горизонтальный очерк определяется окружностью экватора; - фронтальная проекция или фронтальный очерк образуется замкнутой линией главного фронтального меридиана m", полученного при пересечении поверхности вращения фронтальной плоскостью уровня, проходящей через ее ось вращения; - профильная проекция или профильный очерк образуется замкнутой линией главного профильного меридиана n`", полученного при пересечении поверхности вращения профильной плоскостью уровня, проходящей через ее ось вращения; Вращением прямой линии образуются: – цилиндр вращения, если прямая l параллельна оси i (рис. 43 а); – конус вращения, если прямая l пересекает ось i (рис. 43 б); – однополостный гиперболоид, если прямая l скрещивается с осью i (рис. 43 в).
К поверхностям вращения, образованным вращением кривых второго порядка вокруг оси относятся: – сфера образуется вращением окружности вокруг ее диаметра (рис. 44 а); – эллипсоид вращения образуется вращением эллипса вокруг большой или малой оси (44 б, в); – тор образуется вращением окружности вокруг внешней оси (рис. 44 г);
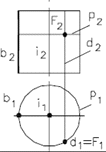
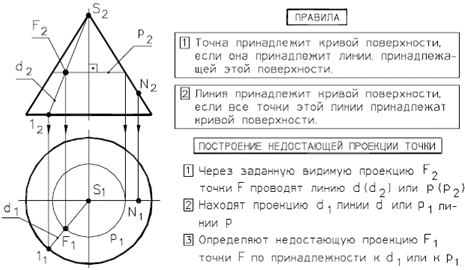
– 38 параболоид вращения образуется вращением параболы вокруг ее оси (рис. 44 д); – однополостный гиперболоид вращения образуется вращением гиперболы вокруг ее мнимой оси. Эта поверхность образуется также вращением прямой (рис. 44 е).  25. Как строится точка на поверхности вращения? Поясните на примере сферической поверхности. Определим недостающие проекции точек на поверхностях вращения. Образующей цилиндра является прямая, па раллельная оси вращения. Образующей конуса является прямая, пере секающая ось вращения. Образующей сферы является окружность, центр которой лежит на оси вращения. Образующей кольца (тора) является окружность, центр которой не лежит на оси вращения. Точка принадлежит кривой поверхности, если она принадлежит линии, принадлежащей этой поверхности.
Построение точек на поверхностях сферы или тора выполняют при помощи параллели или меридиана, проходящих через эту точку. 26. Как образуется прямая винтовая поверхность? Винтовая поверхность может быть образована прямой линией или ее отрезком, окружностью или ее дугой, сферической поверхностью, какой либо кривой и т. п. Винтовая поверхность, образованная винтовым движением прямой линии, относится к поверхностям, называемым линейчатыми геликоидами. Среди них различают прямой геликоид (винтовой коноид), наклонный или архимедов геликоид, эвольвентный и конволютный геликоид. Винтовая поверхность имеет применение в резьбовых изделиях. Прямая винтовая поверхность или прямой геликоид образуется при вращении производящей прямой линии ι, которая пересекает ось i геликоида под прямым углом, вокруг этой оси и одновременном перемещении вдоль нее на расстояние пропорциональное углу поворота. Производящая прямая ι последовательно занимает 12 положений ι0, ι1, ι2, ..., ι12. Пpи одном повороте вокруг оси и эта прямая переместится вдоль нее на расстояние равное шагу h, т. е. на величину расстояния между точками 0 и 12. Производящая прямая при своем перемещении образует геликоидную поверхность, ограниченную двумя соосными винтовыми линиями - направляющими геликоида. 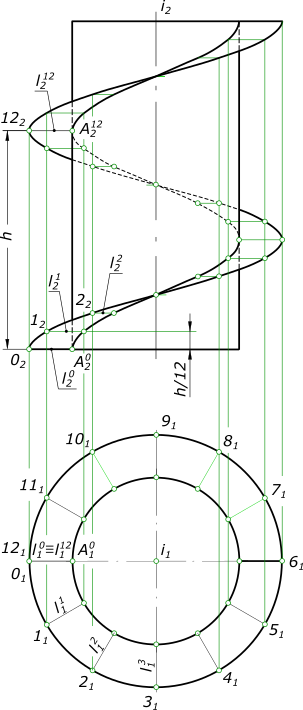 27. Как построить цилиндрическую винтовую линию?  28. Как строится точка пересечения прямой с плоскостью? 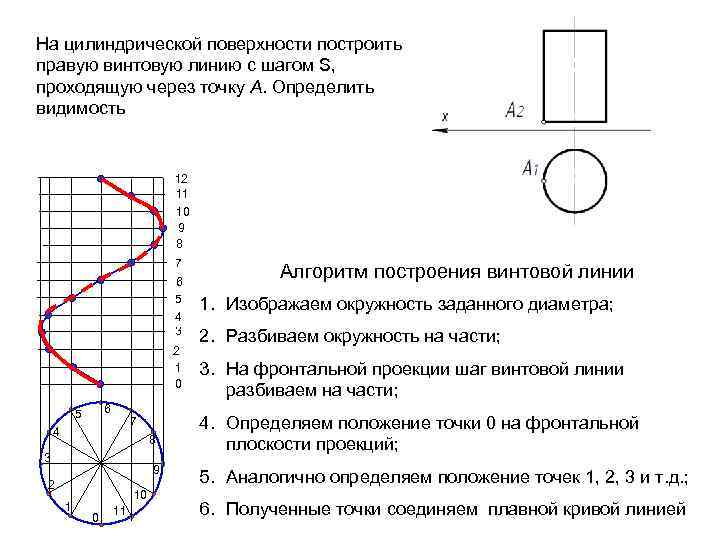 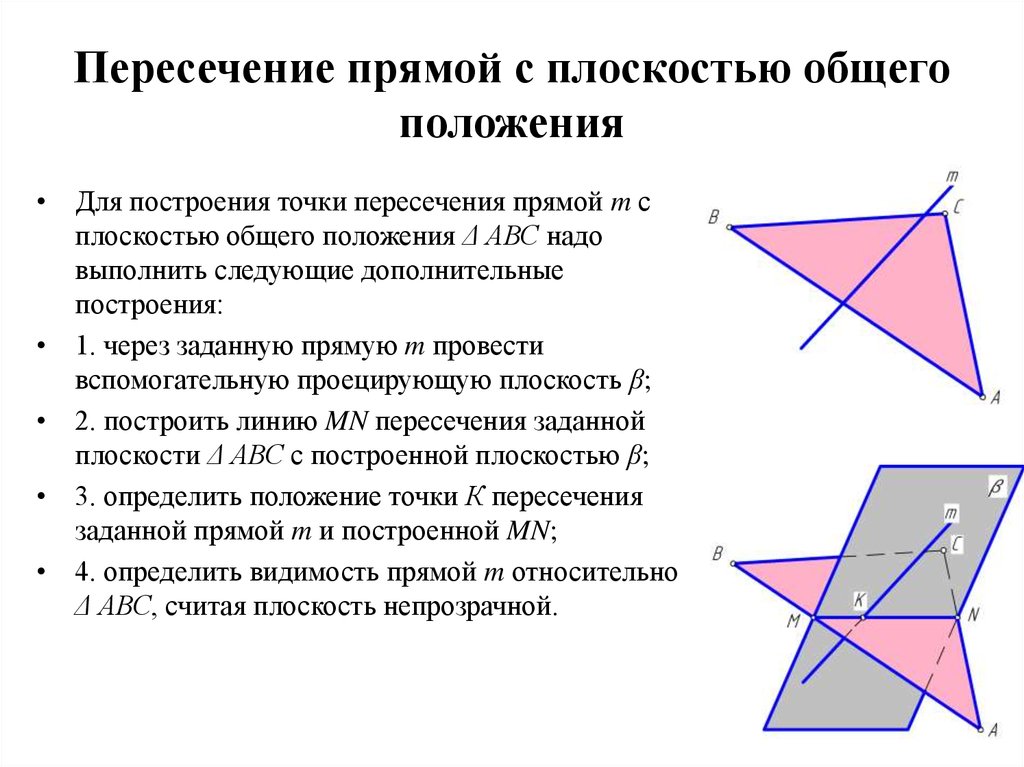 29. Что такое простейшая секущая плоскость? 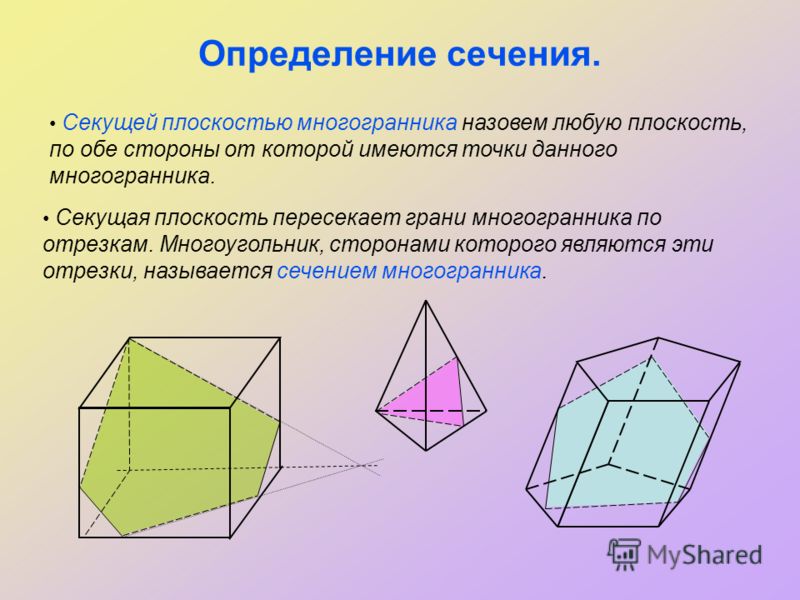 30. Сформулируйте теорему Монжа. Поясните на примере. Теорема : Если две поверхности вращения (второго порядка) описаны вокруг третьей или вписаны в нее, то линия пересечения их распадается на две плоские кривые 2-го порядка. Плоскости этих кривых проходят через точки пересечения линий касания. 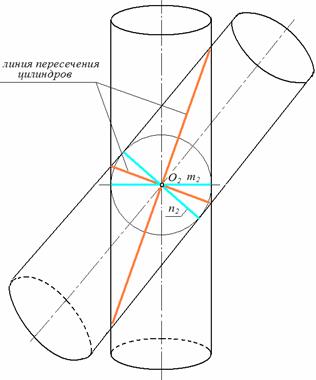 Оси цилиндров пересекаются в точке О. Обе поверхности описаны вокруг третьей – сферы. Сфера пересекает вертикальный цилиндр по окружности m , наклонный цилиндр – по окружности n (в пространстве), на чертеже эти окружности проецируются в прямые, перпендикулярные соответствующим поверхностям . В соответствии с теоремой Монжа, линии пересечения самих цилиндров представляют собой плоские фигуры (эллипсы), которые проходят через общую точку О и точки пересечения линий касания. Оси цилиндров пересекаются в точке О. Обе поверхности описаны вокруг третьей – сферы. Сфера пересекает вертикальный цилиндр по окружности m , наклонный цилиндр – по окружности n (в пространстве), на чертеже эти окружности проецируются в прямые, перпендикулярные соответствующим поверхностям . В соответствии с теоремой Монжа, линии пересечения самих цилиндров представляют собой плоские фигуры (эллипсы), которые проходят через общую точку О и точки пересечения линий касания. | |||||||||||||||||||||||||||||||||||||||||||