начерт. Что изучает начертательная геометрия
 Скачать 1.53 Mb. Скачать 1.53 Mb.
|
Начертательная геометрия является одной из фундаментальных наук, составляющих основу инженерно-технического образования. Она изучает методы изображений пространственных геометрических фигур на плоскостях и способы решения, на основании этих изображений, ме- трических и позиционных задач.
Проецирование– это построение изображения объекта на плоскости (рис. 2.1) с помощью проецирующих лучей, исходящих из одной точки (центра). Полученное в результате проецирования изображение геометрического образа, называют его проекцией,а плоскость, на которую падают проецирующие лучи –плоскость проекций. Проекция любой геометрической фигуры есть множество проекций всех ее точек на соответствующие плоскости проекций. Направление проецирующей прямой l и положение плоскости π1 определяют аппа- рат проецирования. 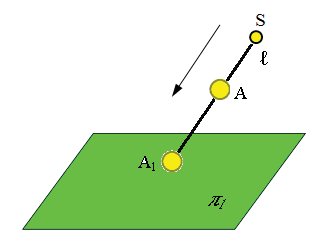
Центральным проецированием называется такое проецирование, при котором все проецирующие лучи исходят из одной точки S – центра проецирования 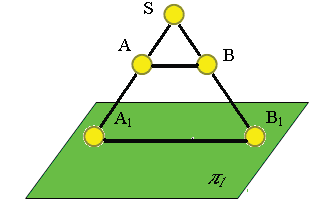 Параллельное проецирование является частным случаем центрального, когда центр проецирования удален в бесконечность от плоскости проекций π1 и все проецирующие прямые параллельны, заданному направлению проецирования S. При заданном аппарате проецирования каждой точке пространства соответствует одна и только одна точка на плоскости проекций. 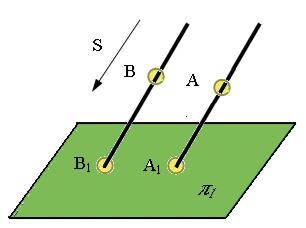
Ортогональное проецирование — это частный случай параллельного проецирования. При ортогональном проецировании проецирующие лучи перпендикулярны к плоскости проекций.
Метод прямоугольного треугольника Прямая общего положения на плоскости проекций отображается с искажением (рис.4.6). Для того чтобы найти её натуральную величину, необходимо воспользоваться правилом прямоугольного треугольни- ка, согласно которому на комплексном чертеже натуральной величи- ной прямой является гипотенуза прямоугольного треугольника, по- строенного на двух катетах. Один из этих двух катетов – это проекция рассматриваемой прямой, а вторым катетом является разность координат начала и конца этой прямой или разность координат z то- чек А и В (Δz = zA – zB). Из точки B1 под углом 900 проводим отрезок |B1B1*|=DZ, полученный в результате построений отрезок A1B1* и будет натуральной величиной отрезка АВ, 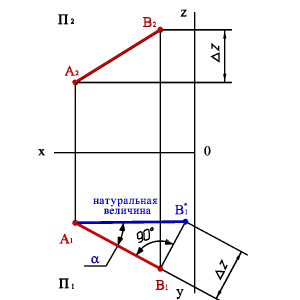 Способ параллельного переноса Параллельный перенос представляет собой перемещение геометрической фигуры параллельно одной из плоскостей проекций. При этом величина проекции фигуры на эту плоскость не меняется. Например, если перемещать отрезок EF параллельно горизонтальной плоскости П1, то длина его проекции E'F' не изменится, когда она займет новое положение E'1F'1 (как это показано на рисунке ниже). Чтобы определить действительный размер отрезка EF, на свободном месте чертежа строим его новую горизонтальную проекцию E'1F'1 = E'F' так, чтобы она была параллельна оси X . Затем по линиям связи находим точки E''1 и F''1. Расстояние между ними и есть искомая величина, поскольку мы перенесли EF в положение, параллельное фронтальной плоскости. 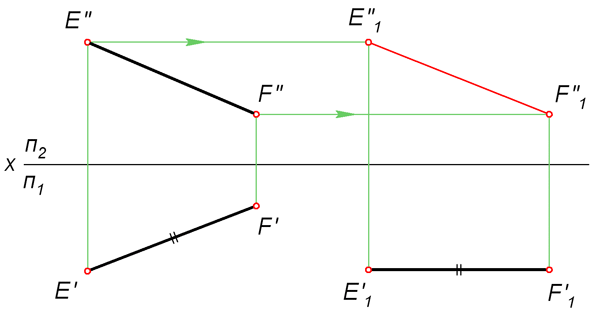 |
