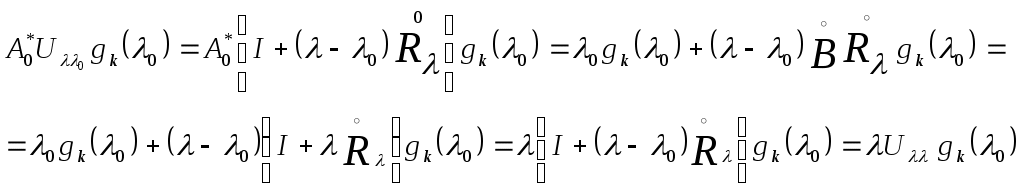является собственным значением кратности является собственным значением кратности  . .
Доказательство. Пусть 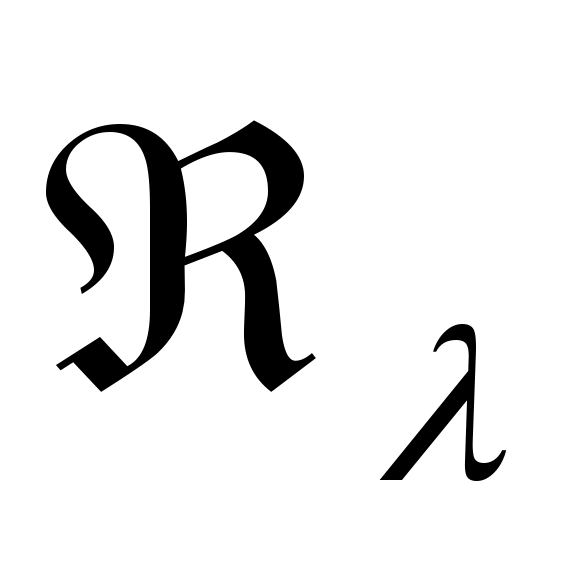 означает линейное многообразие всех решений уравнения означает линейное многообразие всех решений уравнения
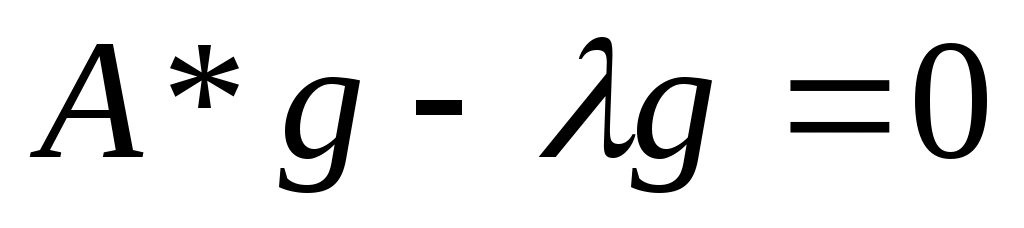 . .
В силу теоремы об инвариантности дефектного числа в поле регулярности число измерений многообразия 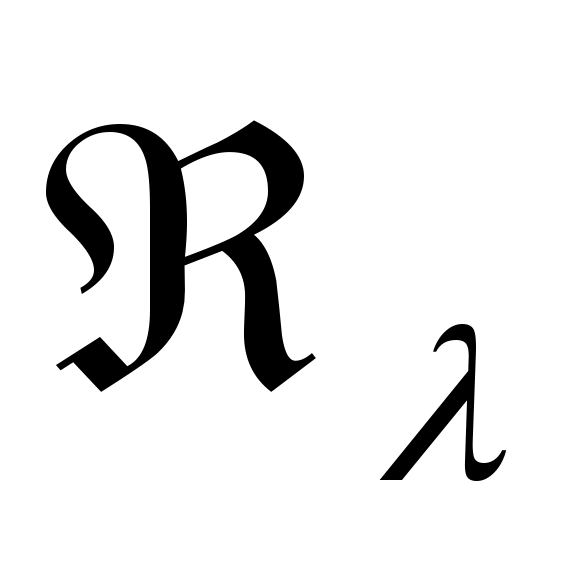 линейно независимы, ибо в противном случае число линейно независимы, ибо в противном случае число  было бы собственным значением оператора А. было бы собственным значением оператора А.
Положим
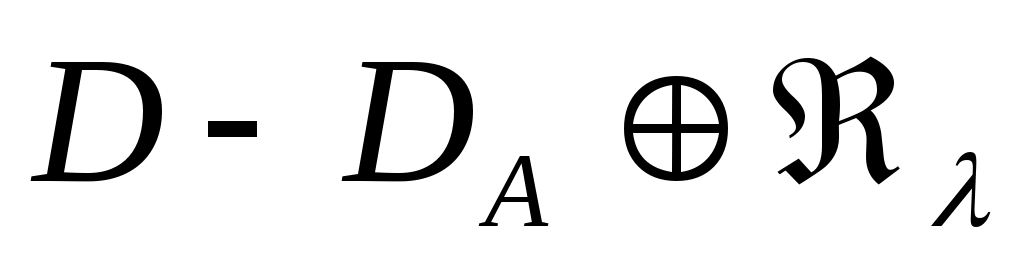 (1) (1)
и пусть 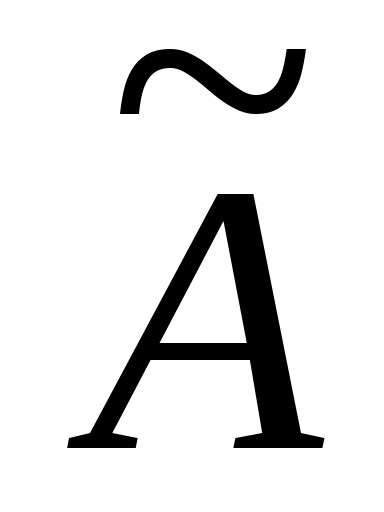 означает оператор, совпадающий с оператором А* на означает оператор, совпадающий с оператором А* на 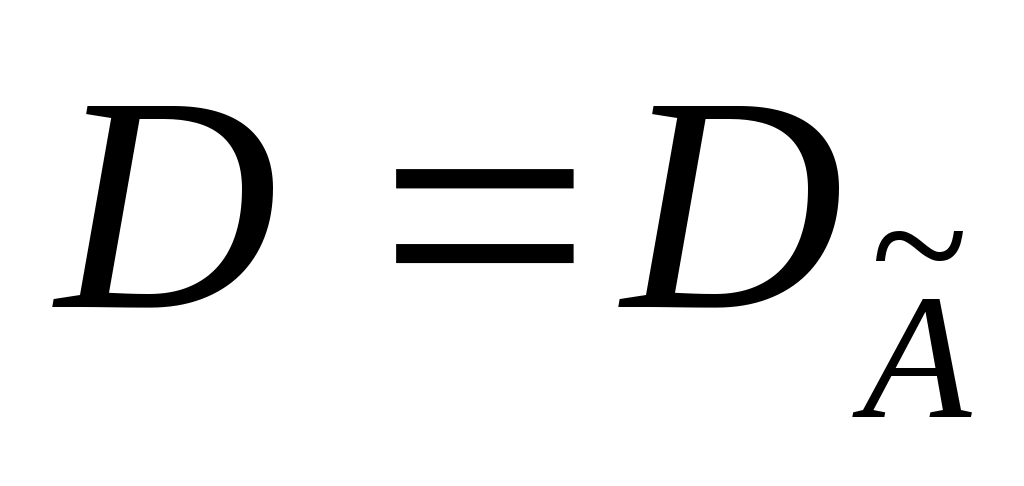 , так что число , так что число  будет собственным значением оператора будет собственным значением оператора 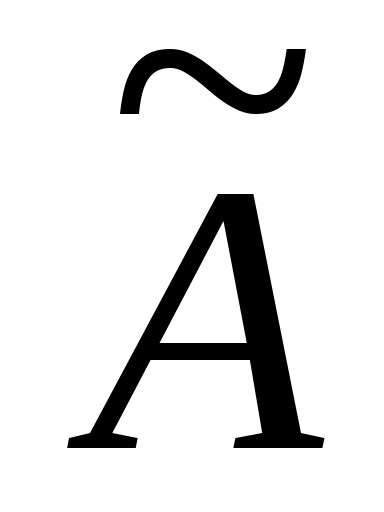 кратности кратности  . .
Покажем, что оператор 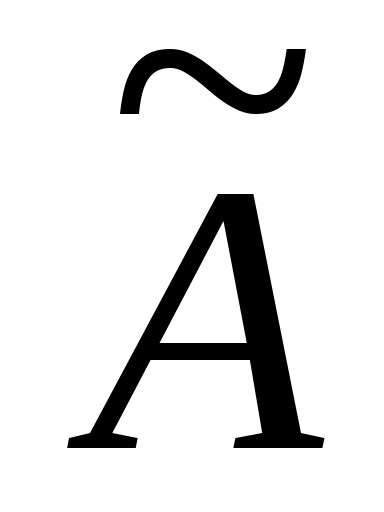 самосопряженный. самосопряженный.
Для этого достаточно установить, что оператор 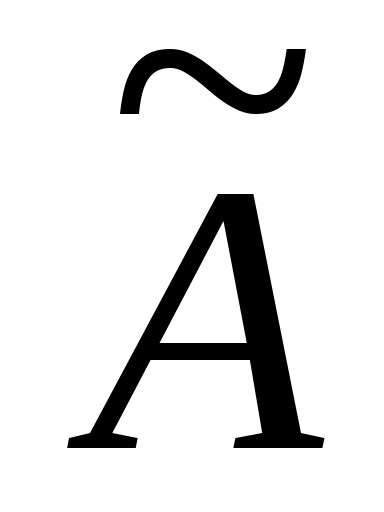 симметрический, ибо из (1) следует, что симметрический, ибо из (1) следует, что
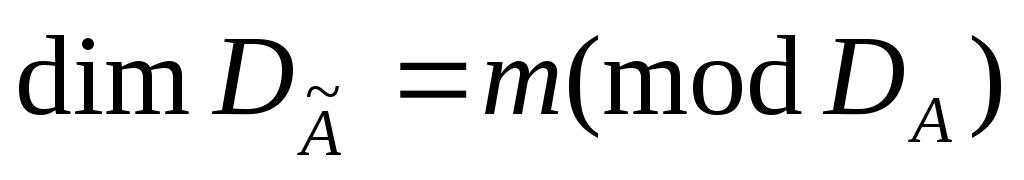 . .
Если  и и 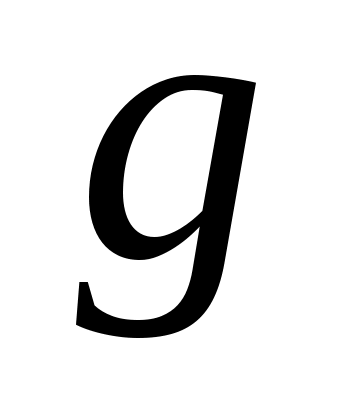 - произвольные элементы из - произвольные элементы из 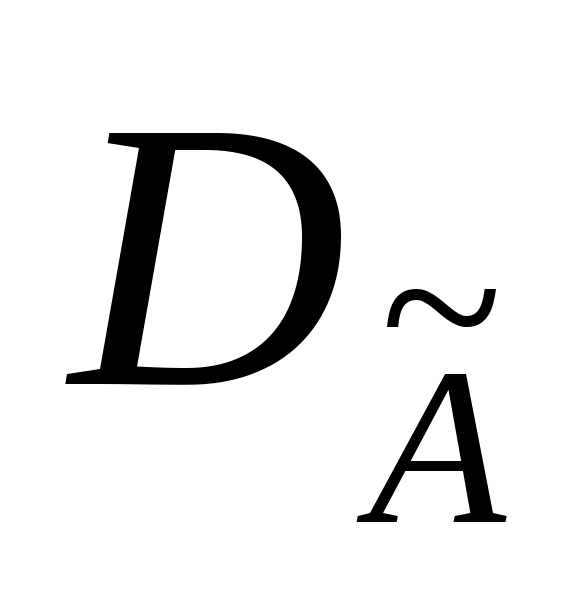 и и
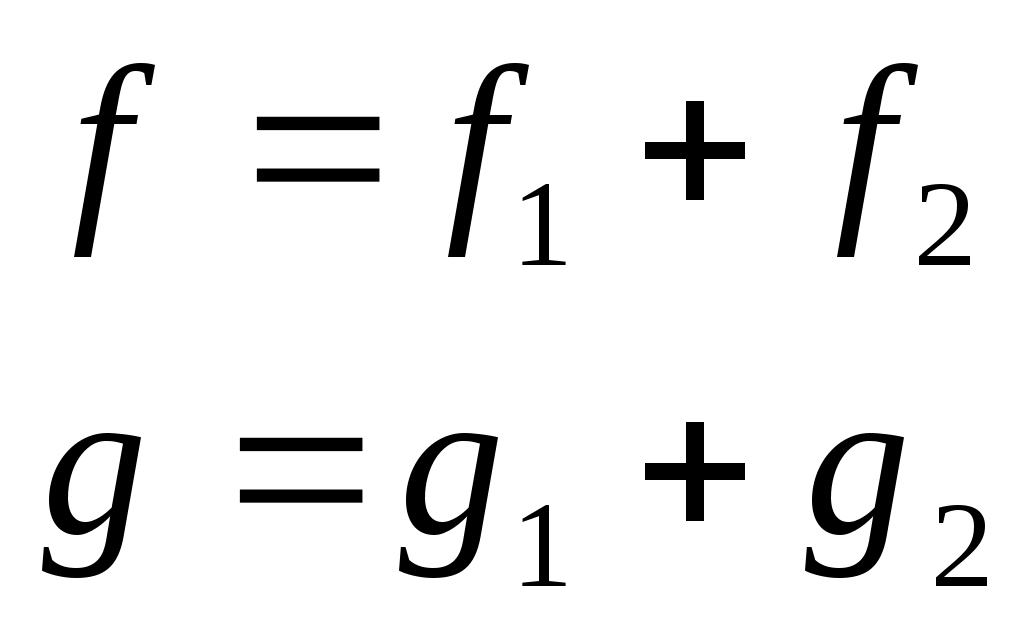 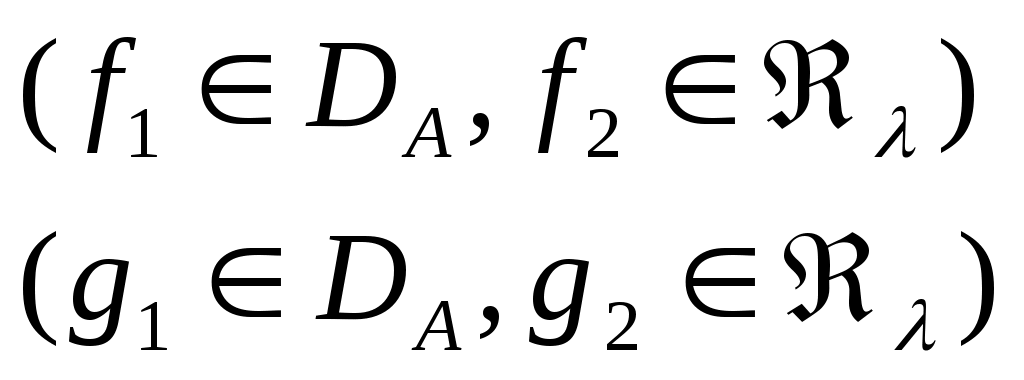
то
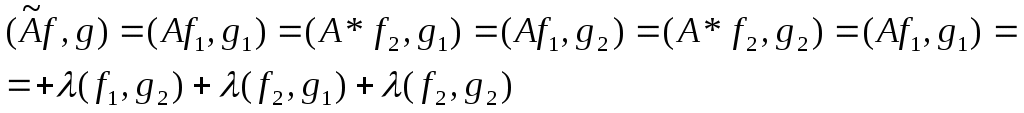
откуда следует симметричность оператора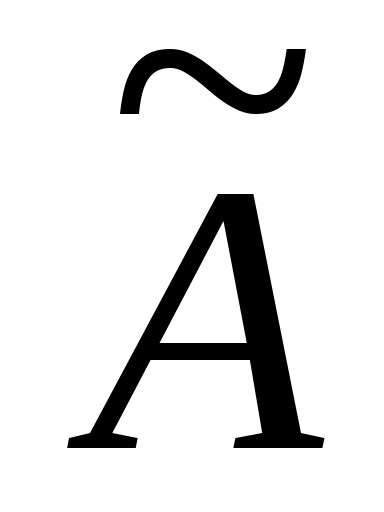 . .
В заключении отметим еще одну теорему, относящуюся к числу решений уравнения
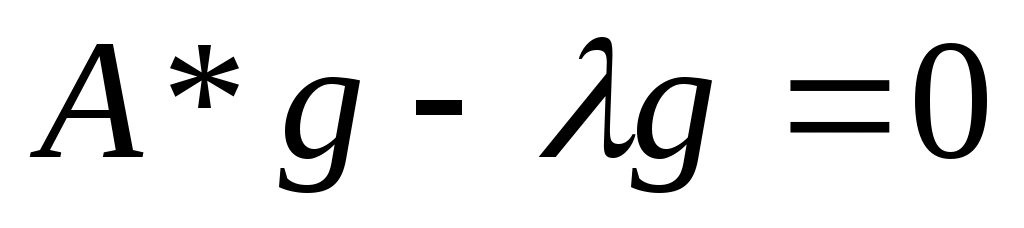
при вещественных  . .
Теорема. Если А – симметрический оператор с индексами дефекта 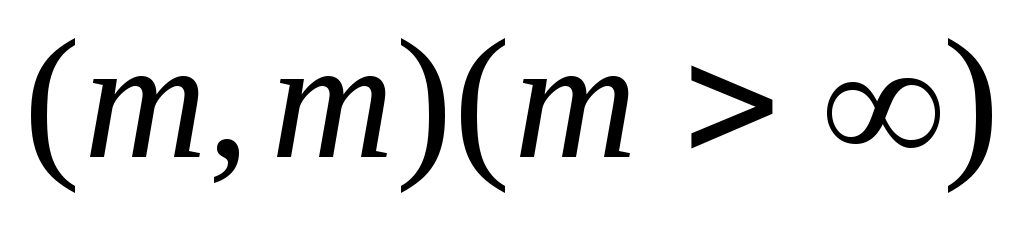 и и  - вещественное число, не принадлежащее точечному спектру оператора А, то число - вещественное число, не принадлежащее точечному спектру оператора А, то число 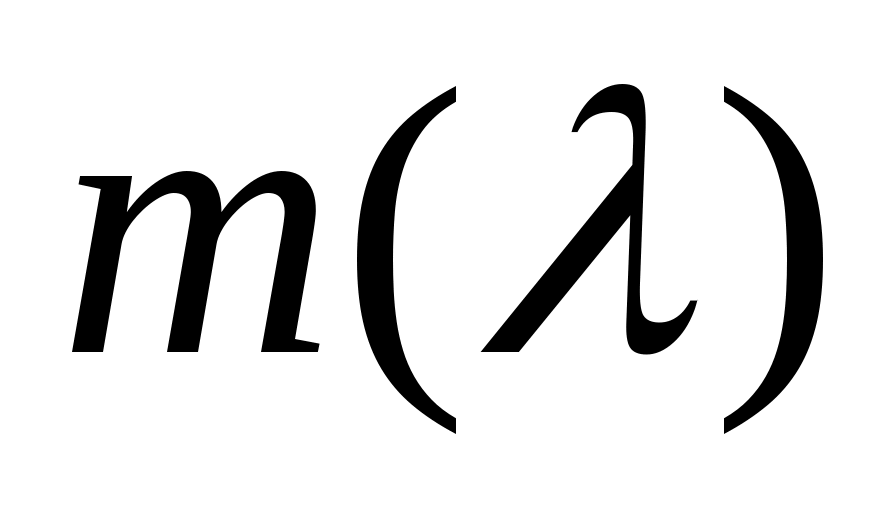 решений уравнения решений уравнения
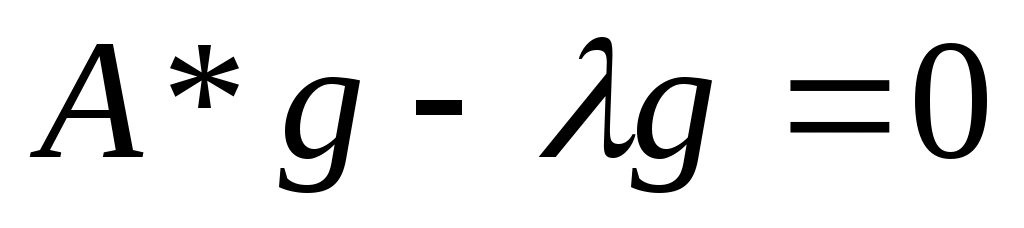 (2) (2)
не превосходит дефектного числа  . .
Для доказательства достаточно построить с помощью многообразия 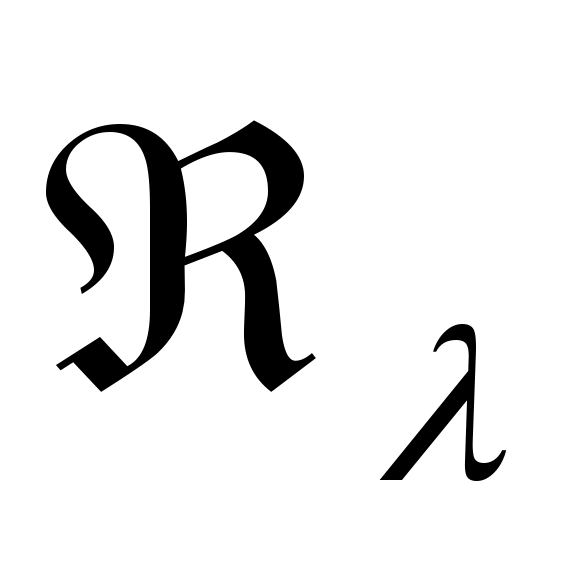 решения уравнения (2) область решения уравнения (2) область 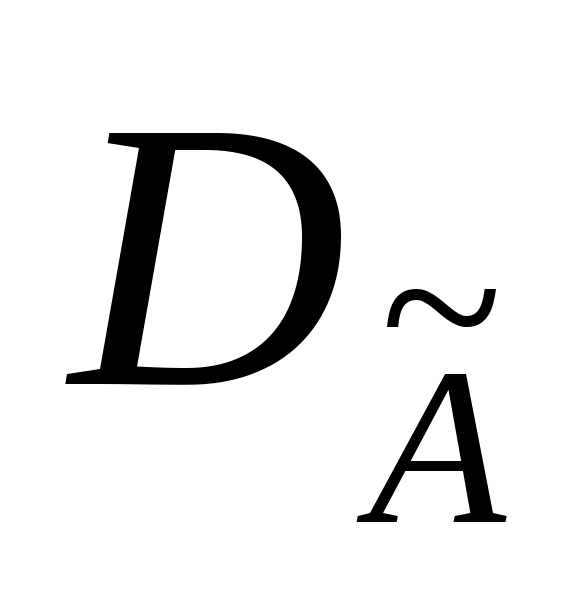 по формуле (1), где основа по формуле (1), где основа  . .
Из доказательства предыдущей теоремы следует, что оператор 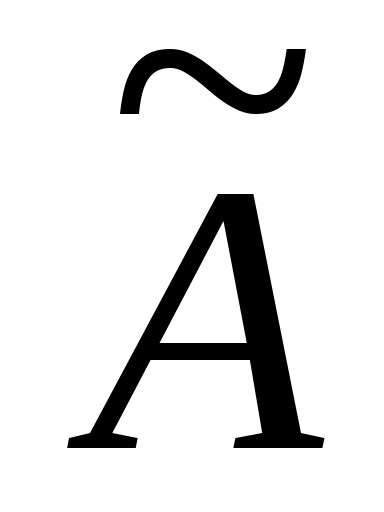 является расширением оператора А и, следовательно является расширением оператора А и, следовательно
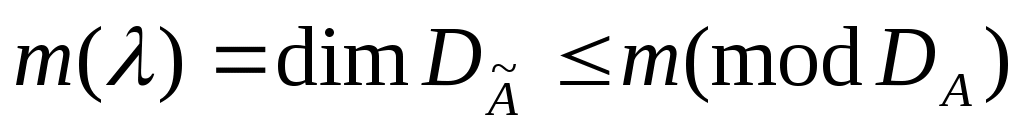 . .
Теорема доказана.
Пусть А1 и А2 – два самосопряженных расширения симметричного оператора А с индексом дефекта 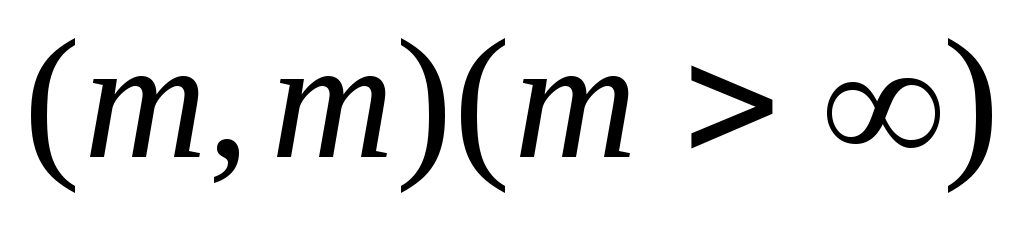 , ,
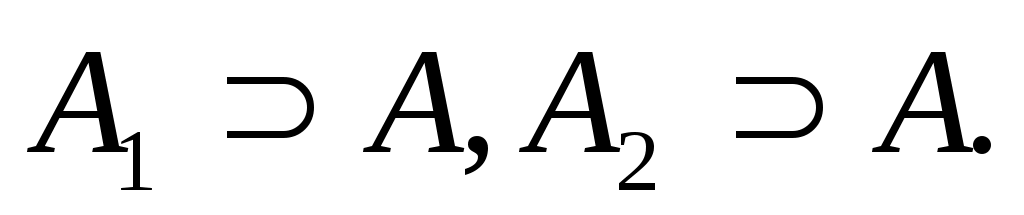
Всякий оператор С, удовлетворяющий условиям
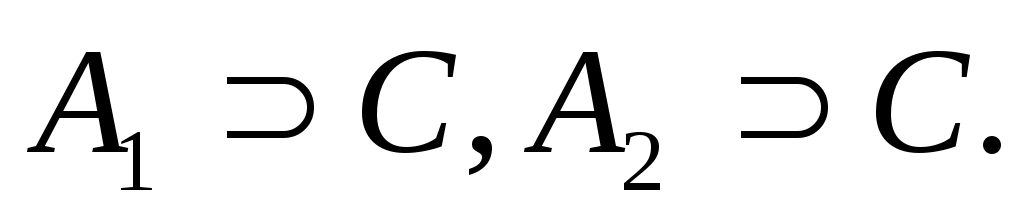 (3) (3)
естественно называть общей частью операторов А1 и А2.
Среди операторов С, удовлетворяющих условиям (3), существует, очевидно, такой, который является расширением любой общей части операторов А1 и А2; такой оператор назовем максимальной общей частью операторов А1 и А2. Максимальная общая часть либо является расширением оператора А, либо совпадает с А; в последнем случае расширения А1 и А2 будем называть взаимно простыми.
Для того чтобы расширения А1 и А2 были взаимно простыми, необходимо и достаточно, чтобы одновременное выполнение условий
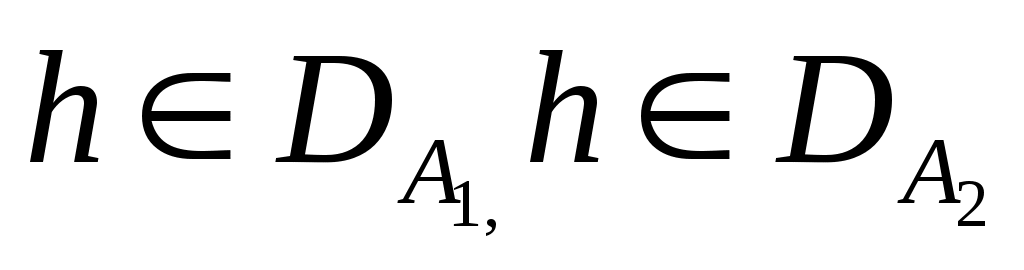 (4) (4)
вело принадлежность  к к 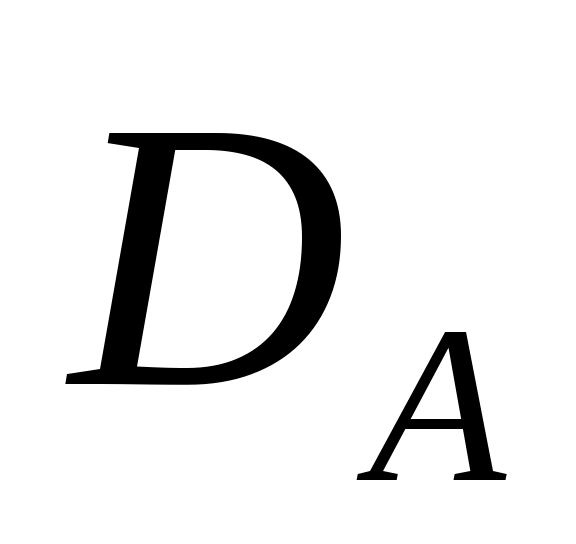 . .
Если максимальное число линейно независимых по модулю 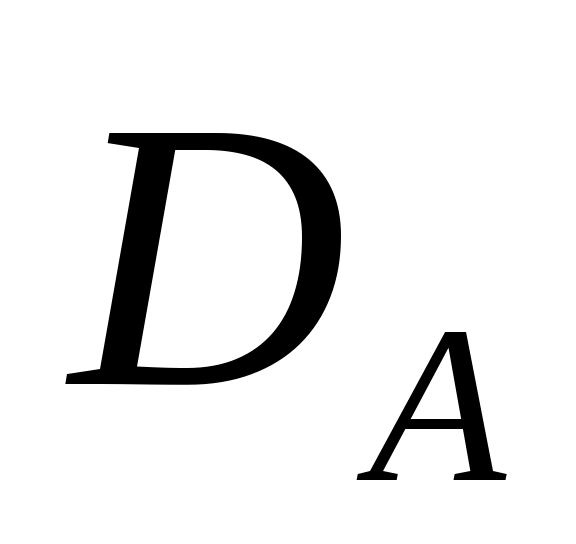 векторов, удовлетворяющих условиям (4), равно векторов, удовлетворяющих условиям (4), равно 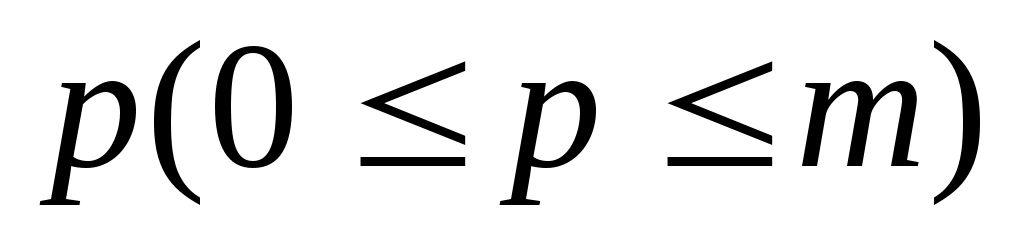 , то максимальная общая часть А0 операторов А1 и А2 имеет индексы дефекта , то максимальная общая часть А0 операторов А1 и А2 имеет индексы дефекта 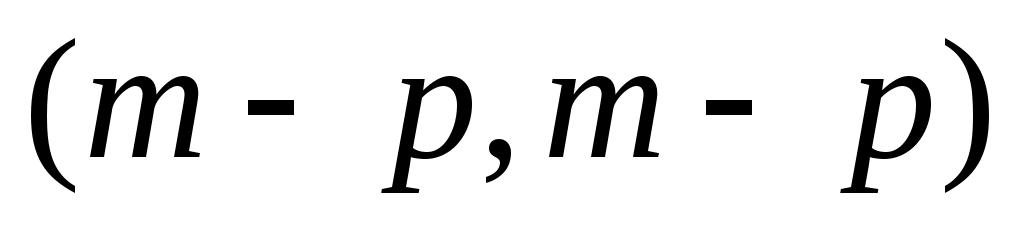 . В этом случае операторы А1 и А2 могут рассматриваться как взаимно простые самосопряженные расширения оператора А0. . В этом случае операторы А1 и А2 могут рассматриваться как взаимно простые самосопряженные расширения оператора А0.
Задачей настоящего пункта является вывод формулы, связывающей резольвенты двух самосопряженных расширений оператора А. Пусть 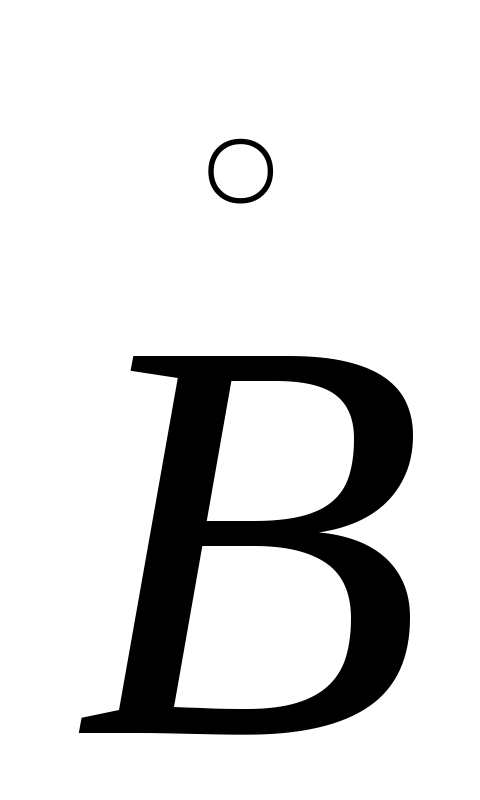 - фиксированное самосопряженное расширение, а - фиксированное самосопряженное расширение, а 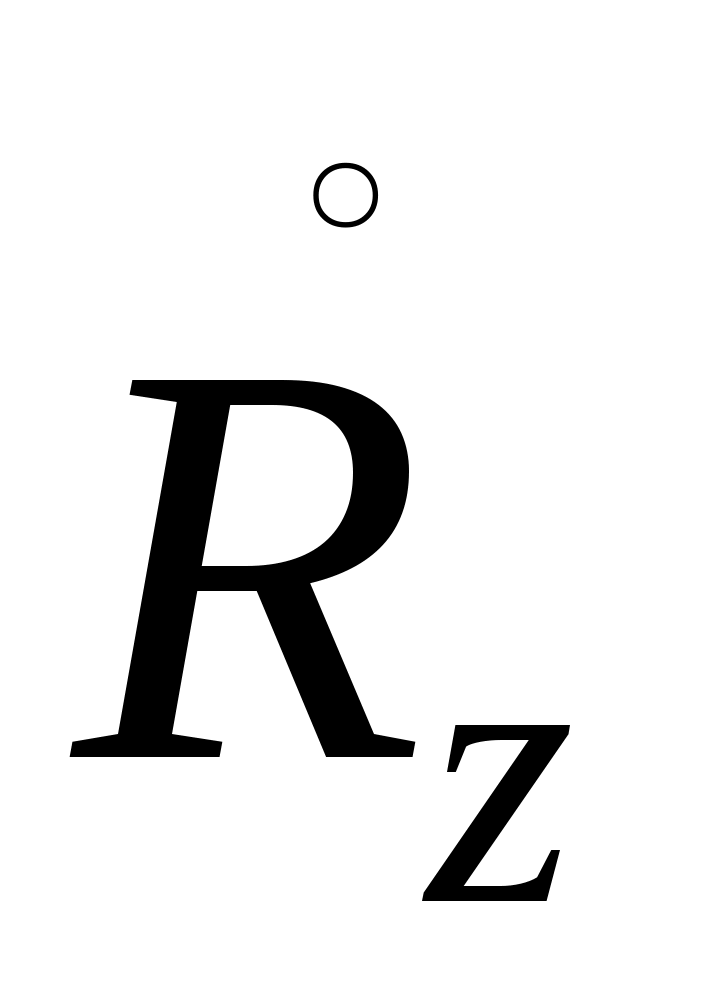 и и 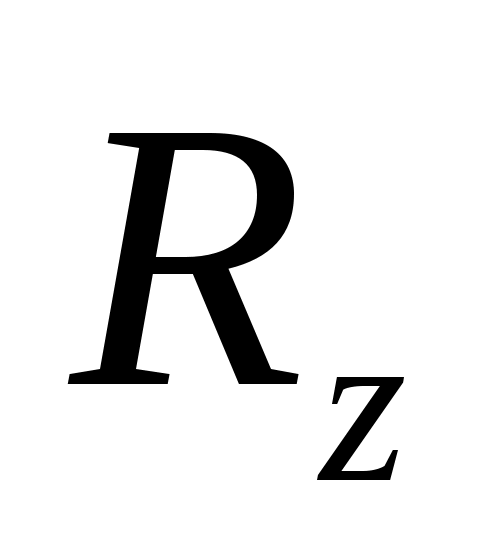 - их резольвенты. Пусть, далее - их резольвенты. Пусть, далее  - любая общая точка регулярности операторов - любая общая точка регулярности операторов  и В (в частности, и В (в частности,  может быть произвольным невещественным числом). может быть произвольным невещественным числом).
Чтобы не выделять случая, когда  и В не являются взаимно простыми расширениями оператора А, будем рассматривать их как взаимно простые расширения их максимальной общей части А0, имеющей индексы (r, r), где и В не являются взаимно простыми расширениями оператора А, будем рассматривать их как взаимно простые расширения их максимальной общей части А0, имеющей индексы (r, r), где 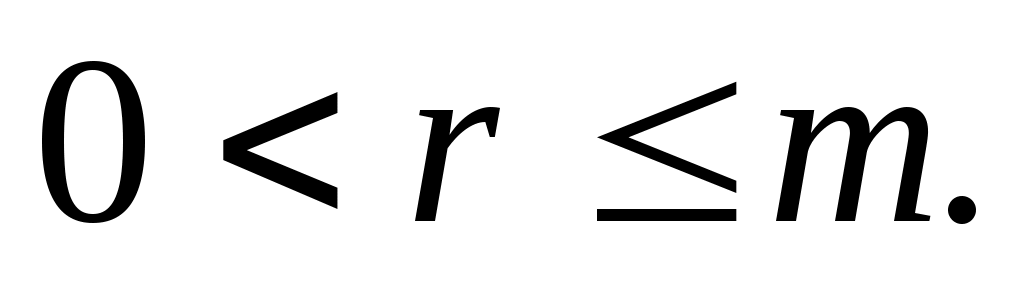
Положим 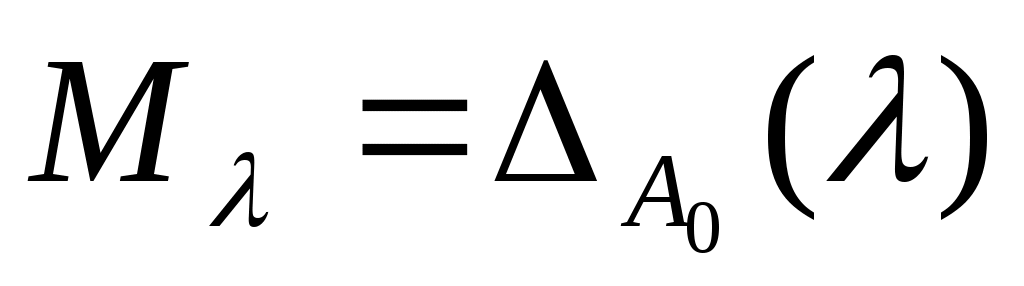 и и 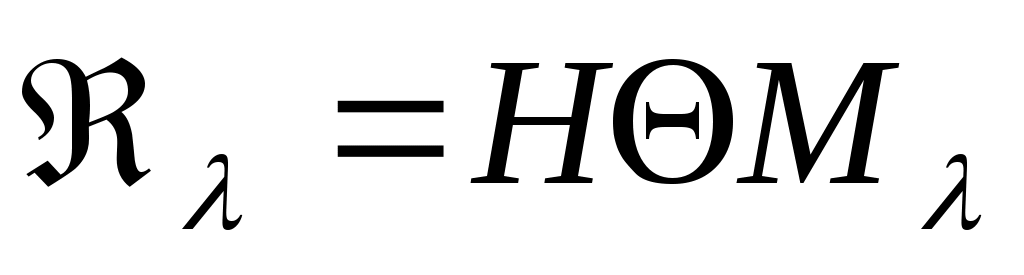 . Для разности резольвент будем иметь . Для разности резольвент будем иметь
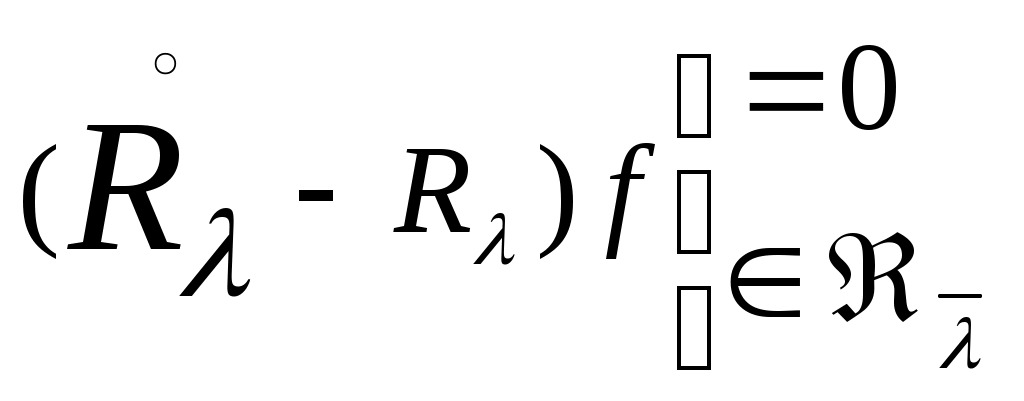 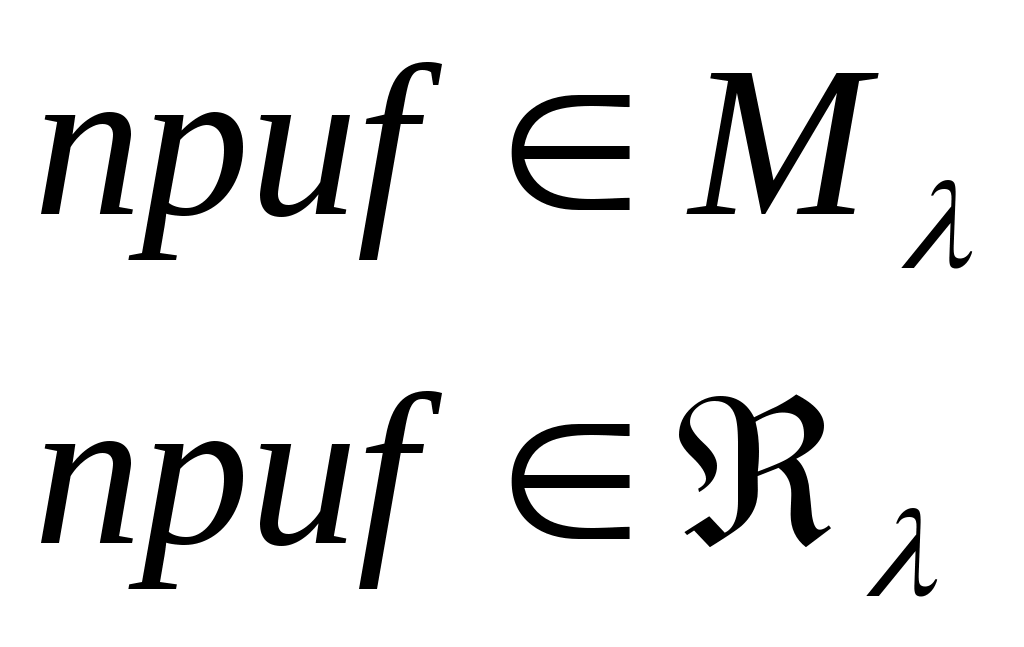 (5) (5)
Последнее вытекает из того, что при любом 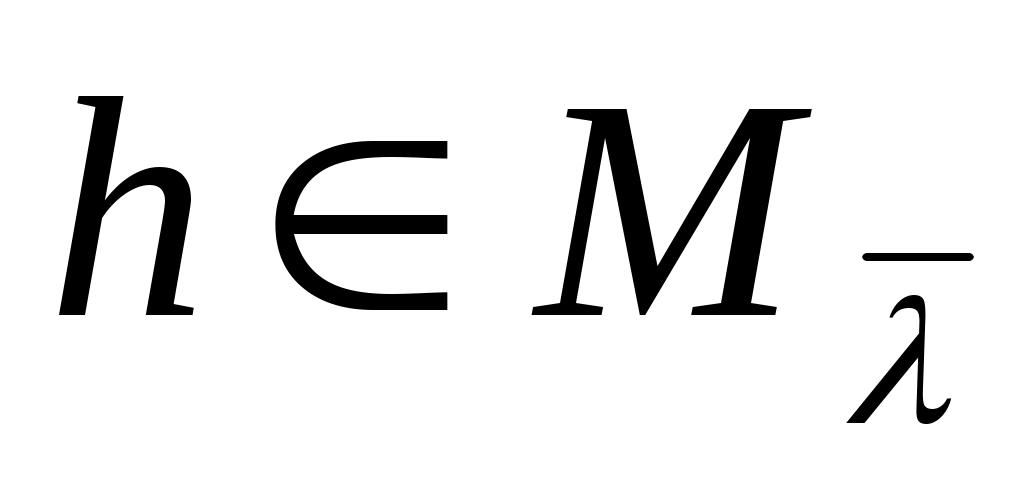
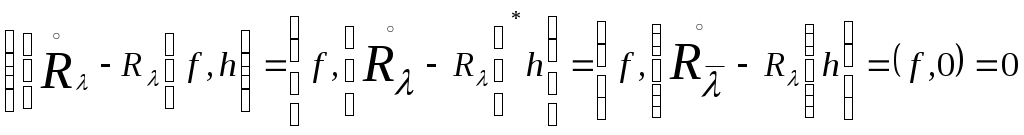 . .
Выберем как-нибудь  линейно независимых векторов линейно независимых векторов 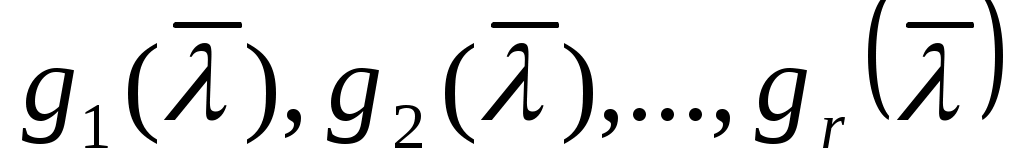 из из 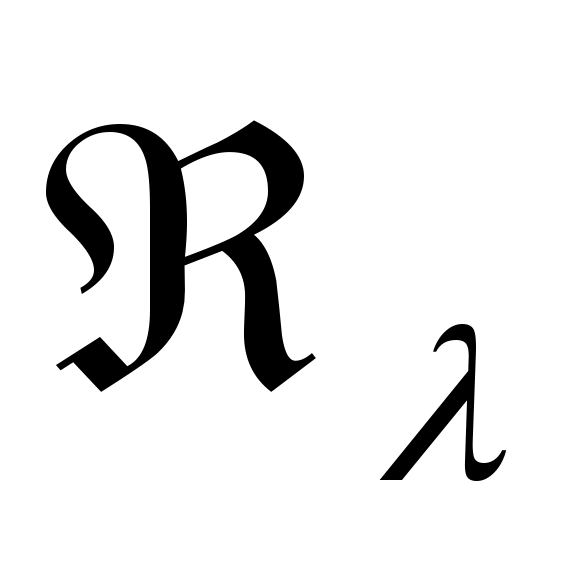 и и  линейно независимых векторов линейно независимых векторов 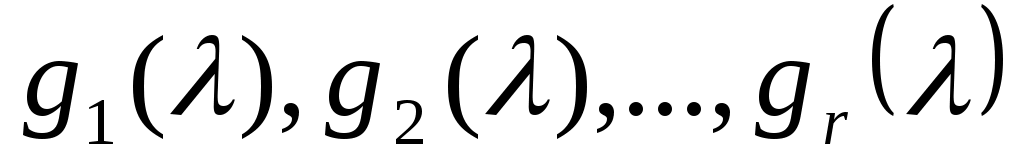 из из  . Из (3) для любого . Из (3) для любого  следует следует
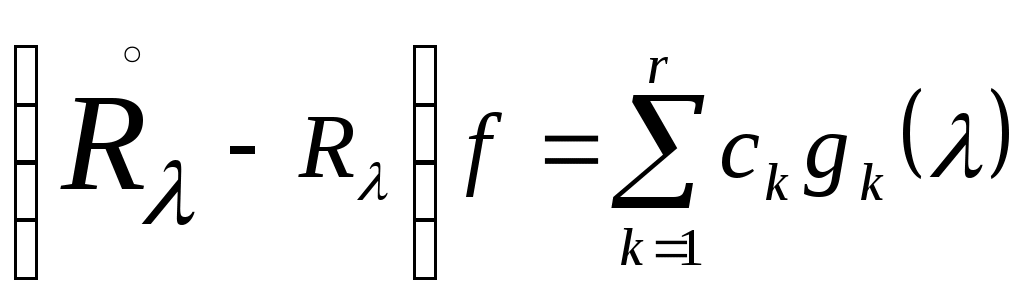 . (6) . (6)
Согласно (4) константы 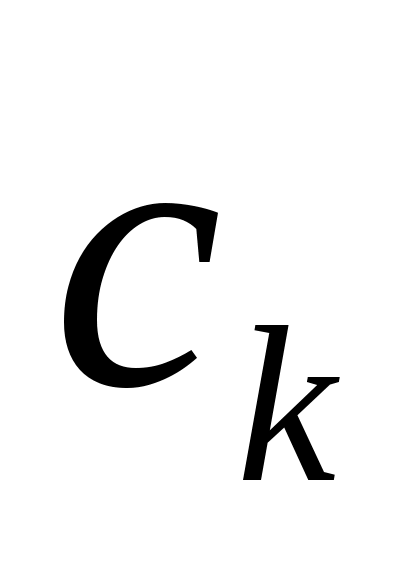 являются линейными функционалами от являются линейными функционалами от  , и можно положить , и можно положить 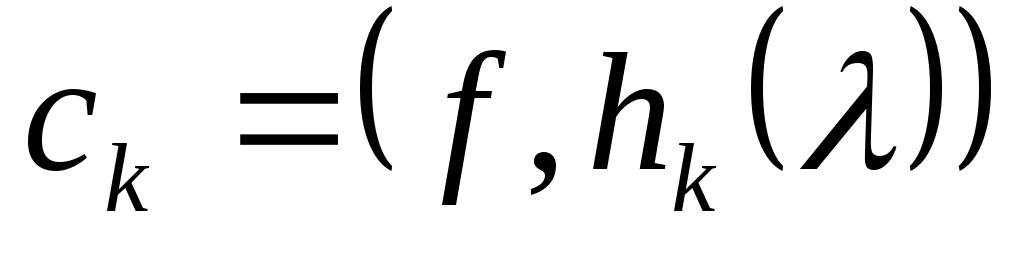 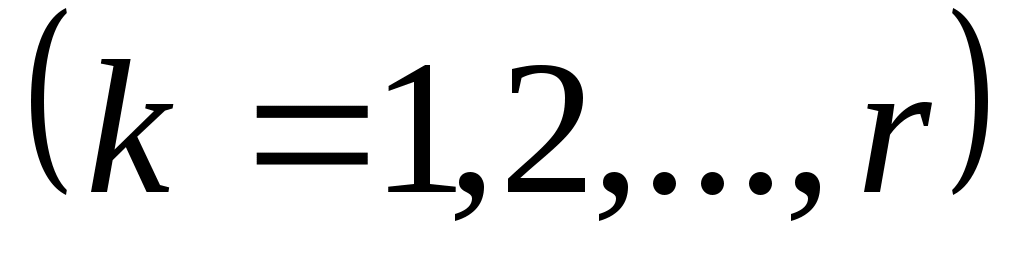 . .
Так как, в силу (5) и линейной независимости векторов 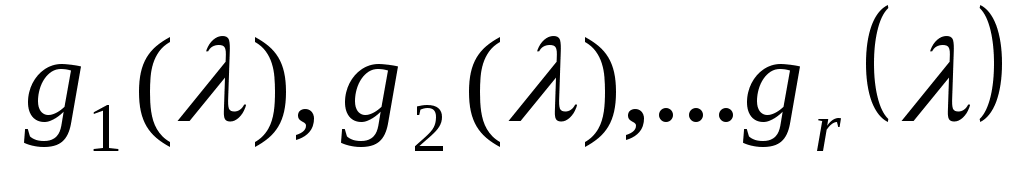 , при любом , при любом  , ортогональном к , ортогональном к  , должно быть , должно быть
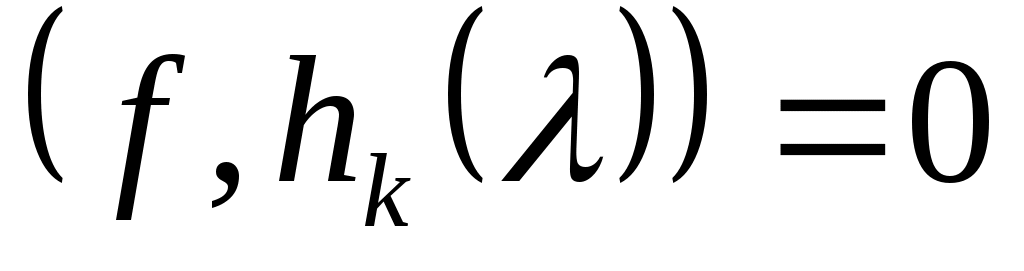 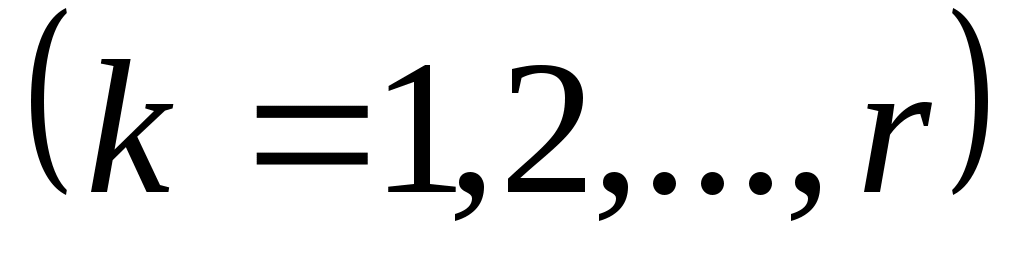 , ,
то 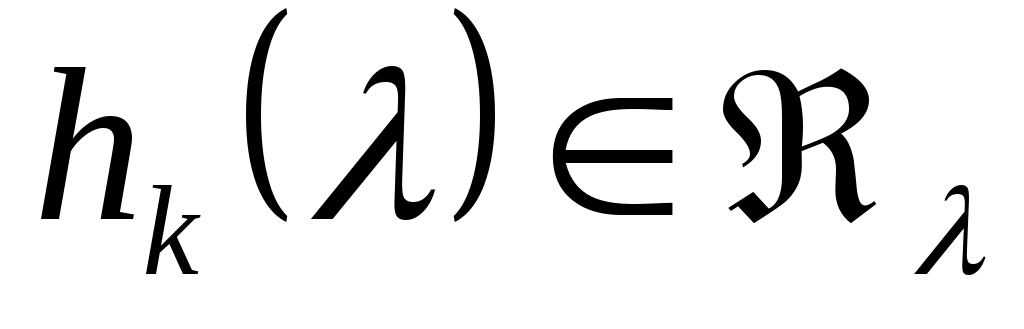 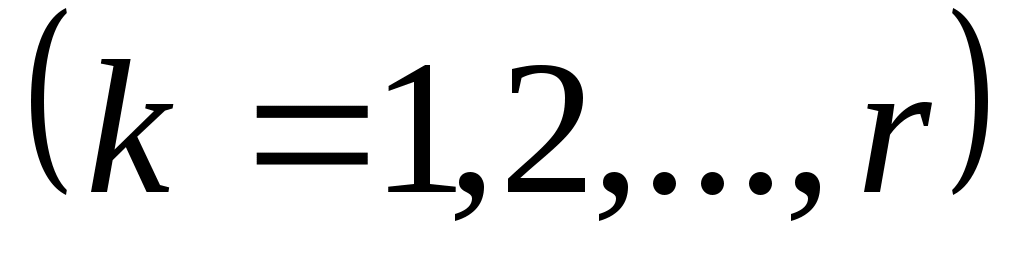 , ,
т.е. 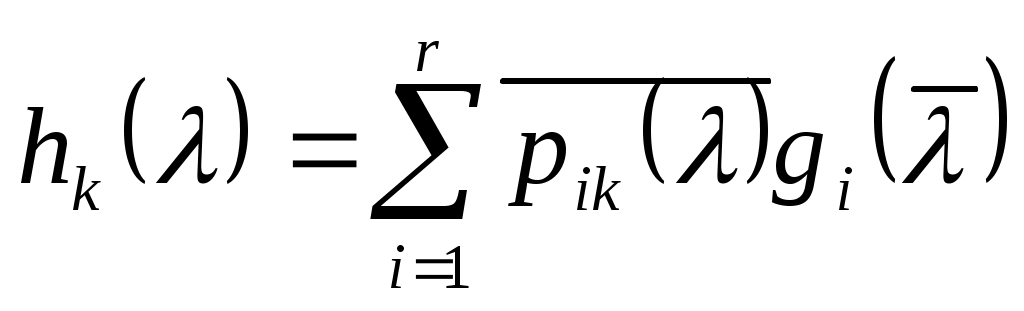 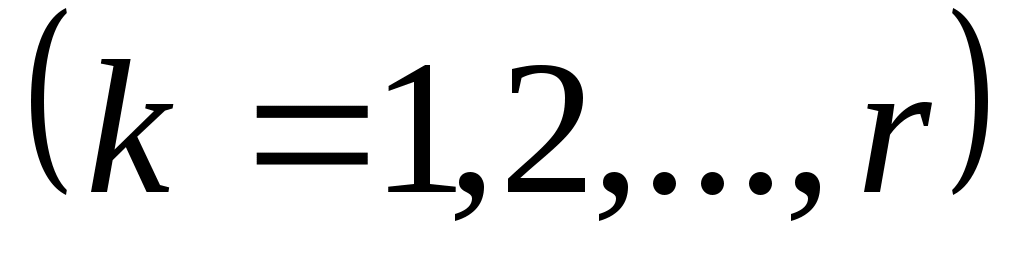 , (7) , (7)
и (4) принимает вид
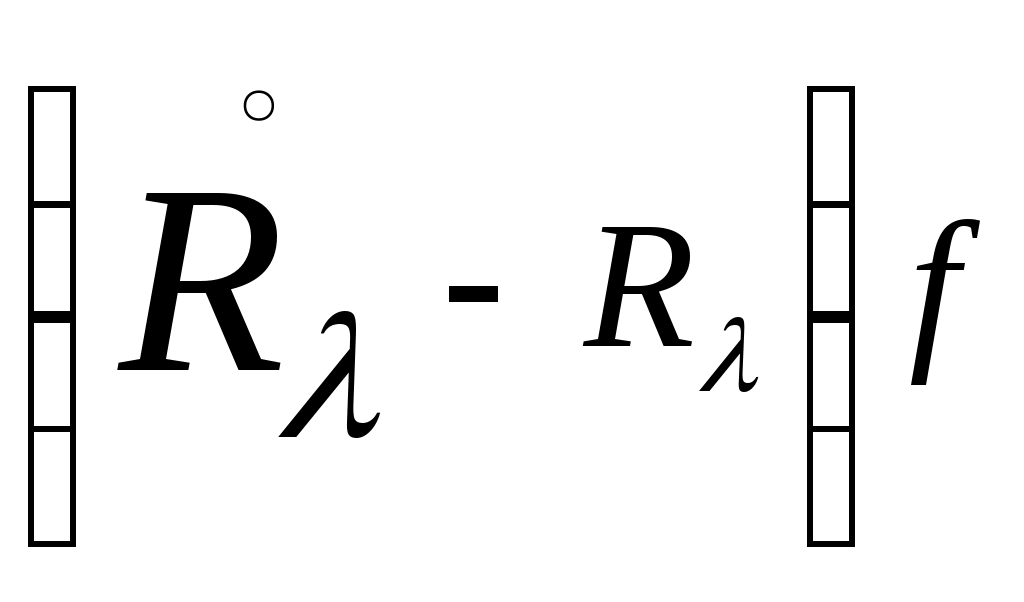 = =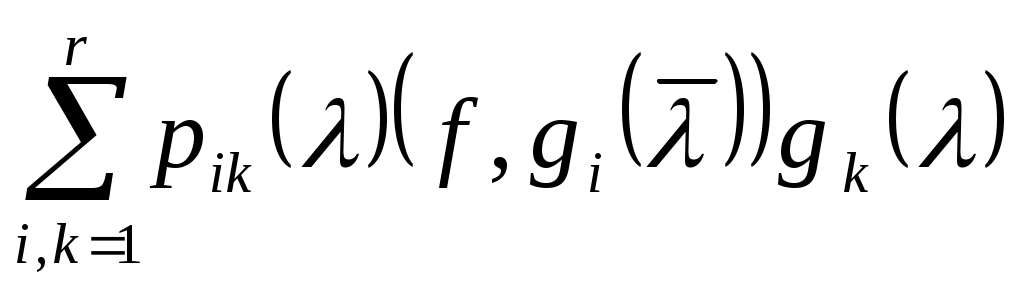 . (8) . (8)
Заметим, что матричная функция 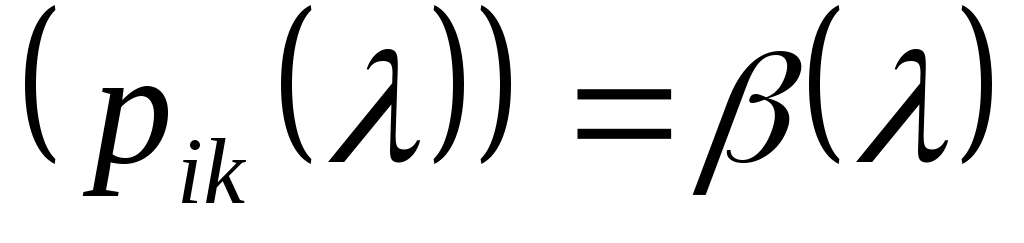 , определенная на множестве общих точек регулярности операторов , определенная на множестве общих точек регулярности операторов  и и  , является неособенной. , является неособенной.
Предположение 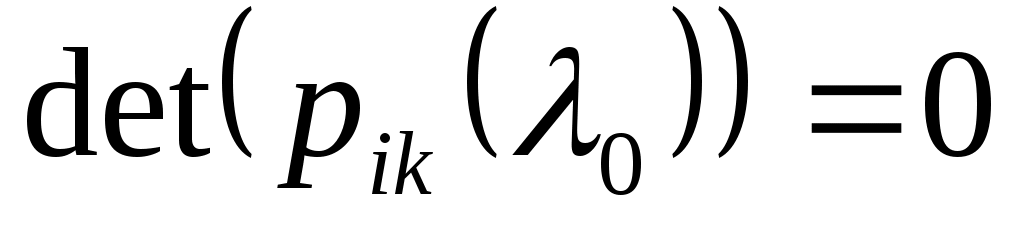 влечет в силу (7) линейную зависимость векторов влечет в силу (7) линейную зависимость векторов 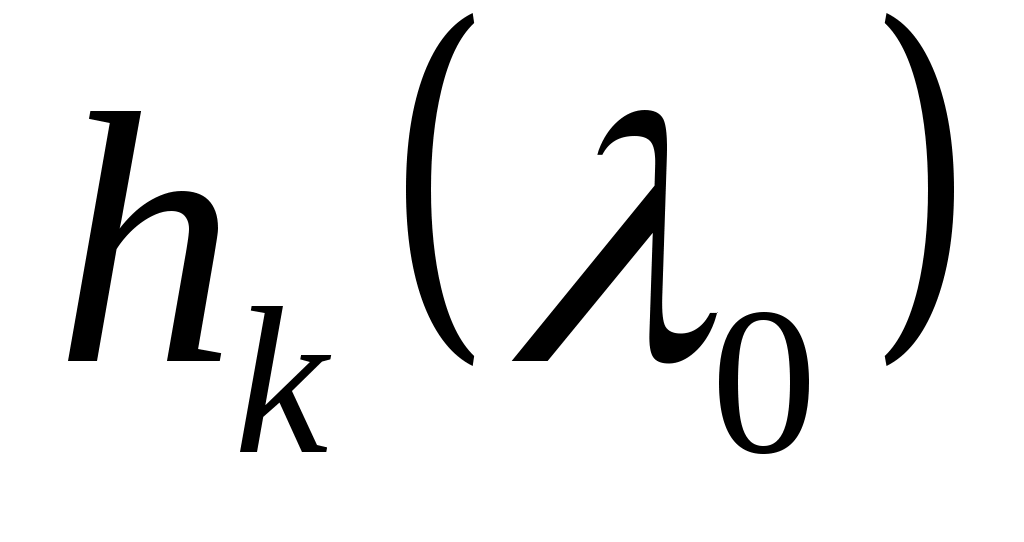 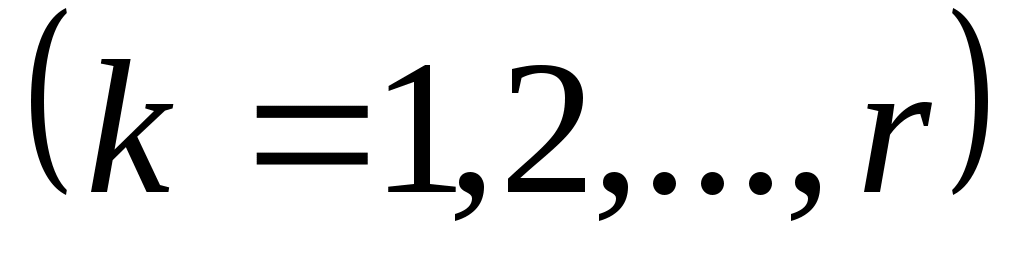 , что означает существование вектора , что означает существование вектора 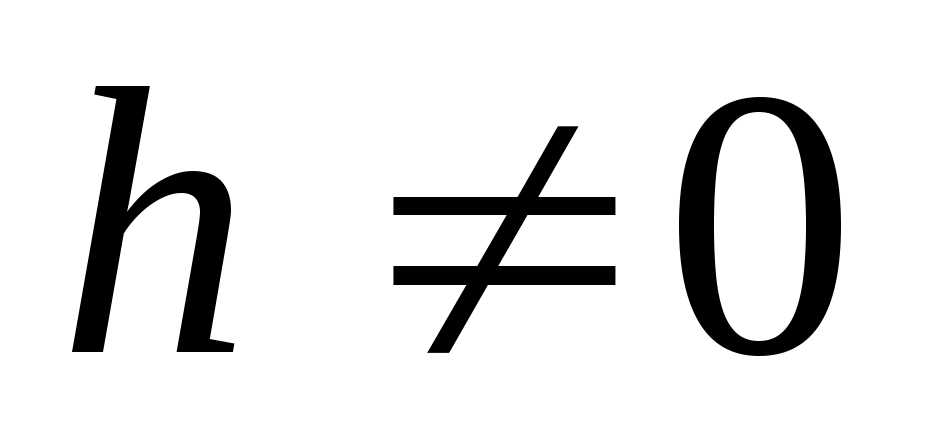 , удовлетворяющего условиям , удовлетворяющего условиям 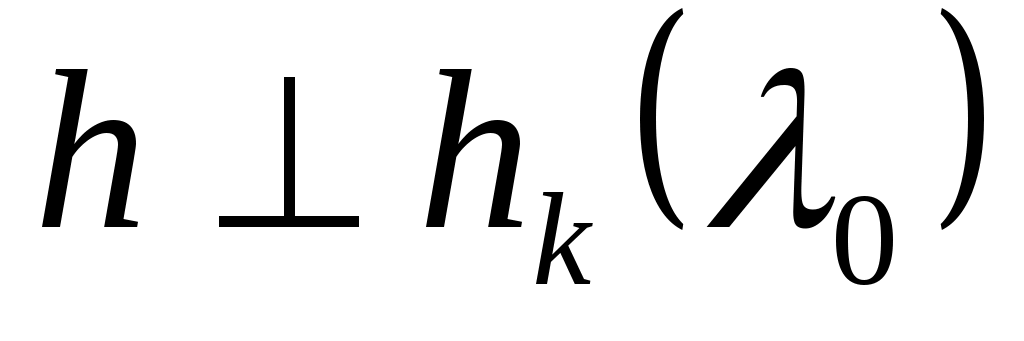 , ,  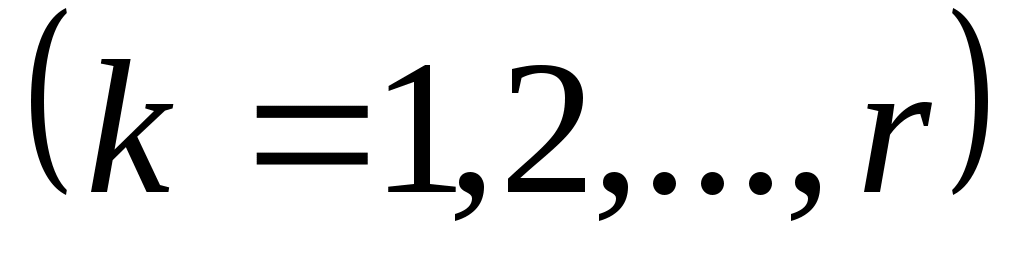 . .
Для вектора  получаем из (6) получаем из (6) 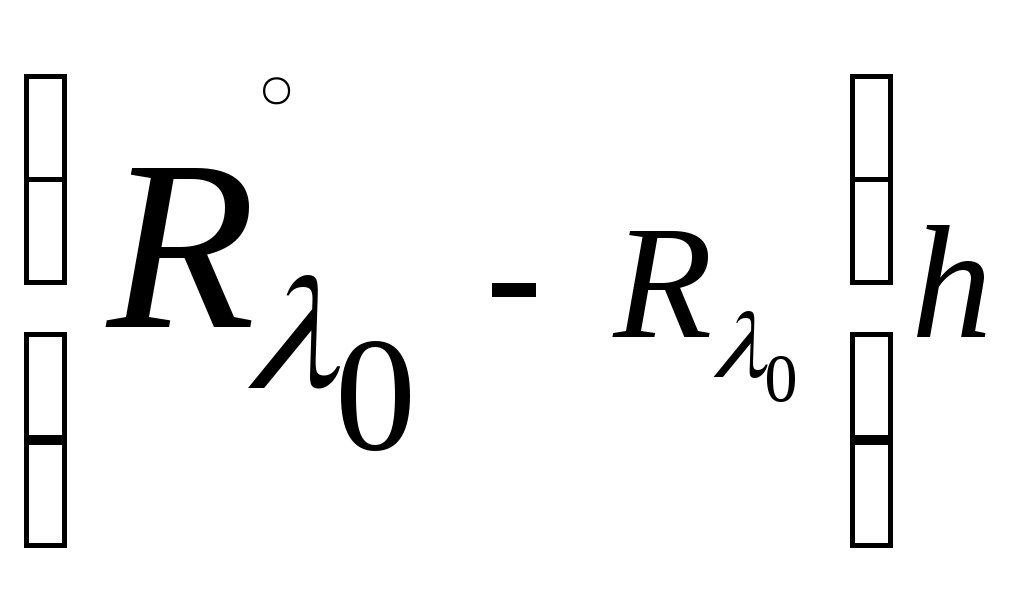 =0, а это противоречит взаимной простоте операторов =0, а это противоречит взаимной простоте операторов 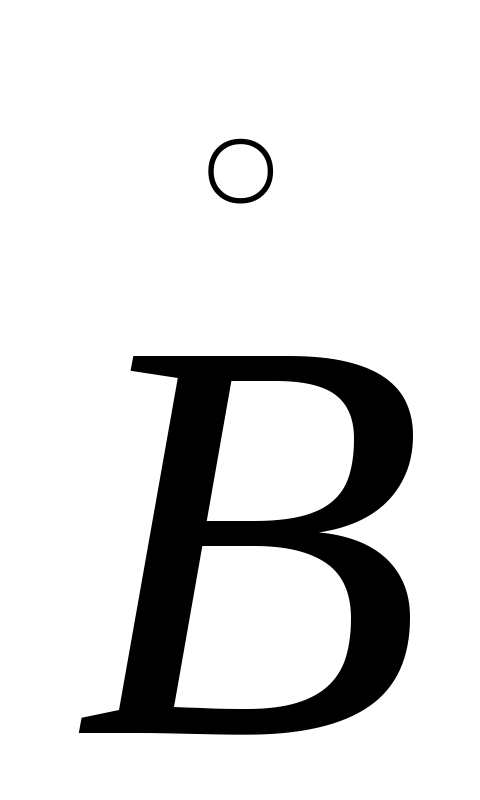 и и 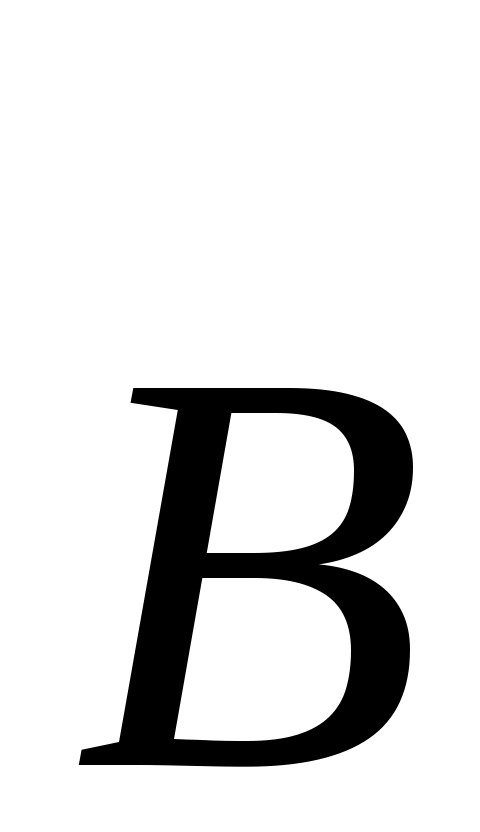 , как расширений оператора , как расширений оператора 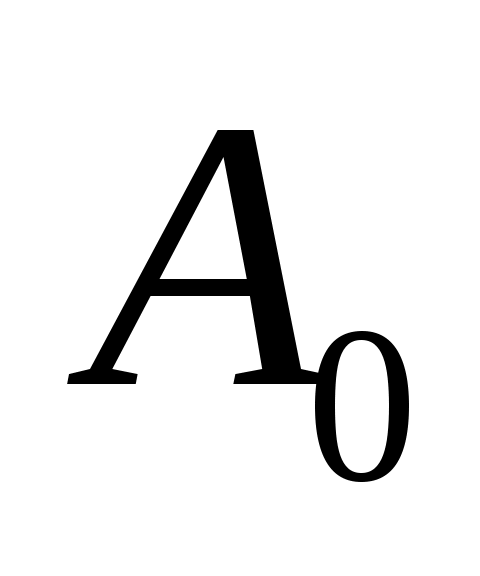 . .
Опуская в (8) элемент  и рассматривая и рассматривая 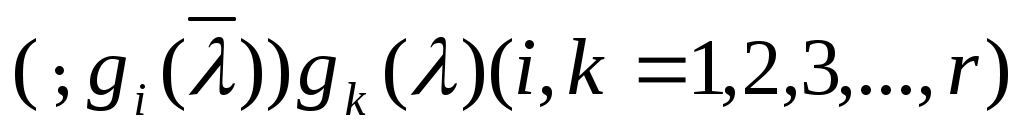 как операторы, получаем для любого значения как операторы, получаем для любого значения  из множества общих точек регулярности операторов из множества общих точек регулярности операторов  и В формулу и В формулу
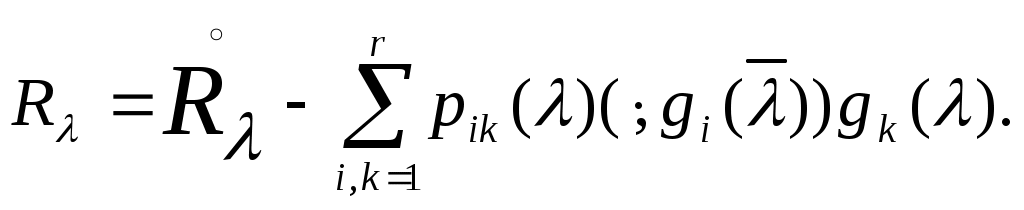 (9) (9)
Левая и правая части формулы (8) являются регулярными аналитическими вектор-функциями от  . Покажем, что . Покажем, что 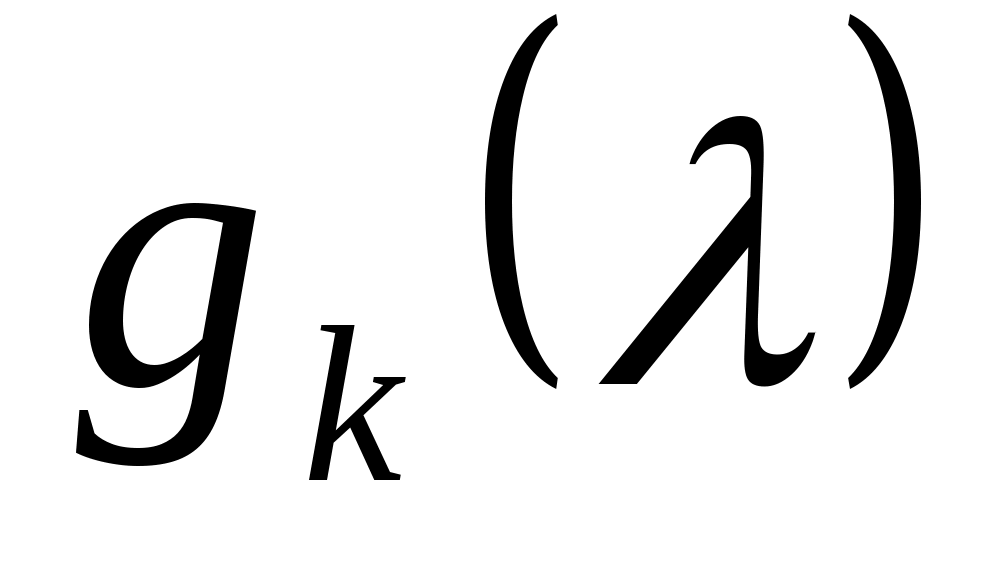 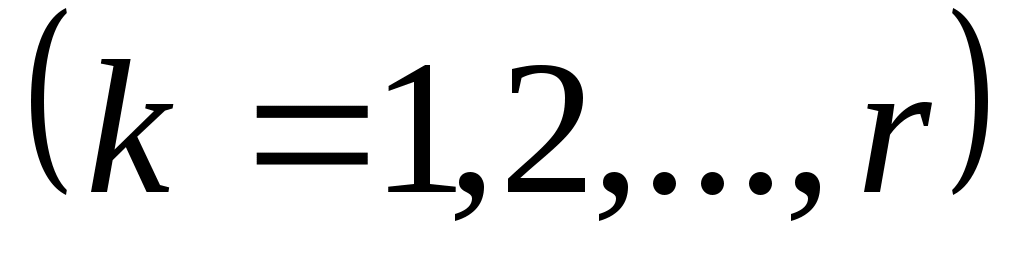 могут быть определены как регулярные аналитические вектор-функции от могут быть определены как регулярные аналитические вектор-функции от  , и получим соответствующую этому выбору формулу для матричной функции , и получим соответствующую этому выбору формулу для матричной функции 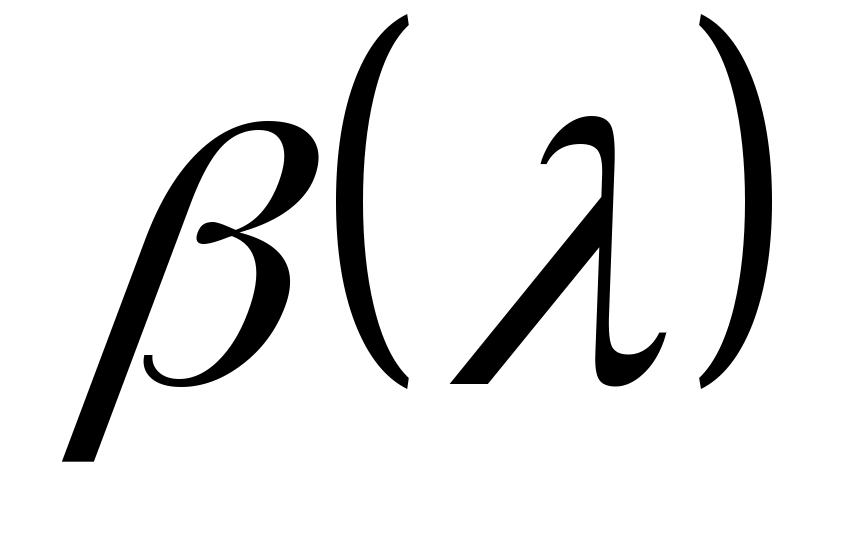 . .
С этой целью возьмем какое-нибудь фиксированное значение  и введем оператор и введем оператор 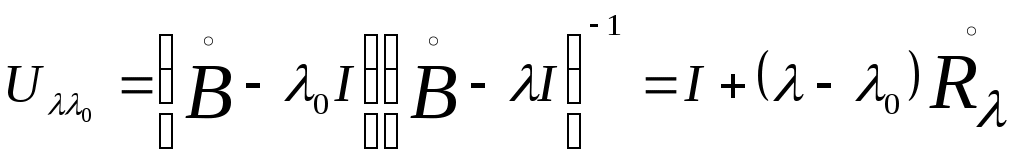 с областью определения с областью определения 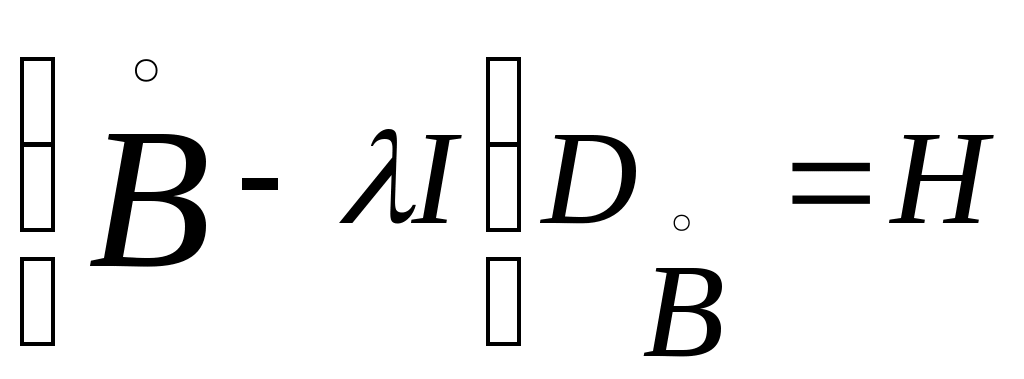 и областью значений и областью значений 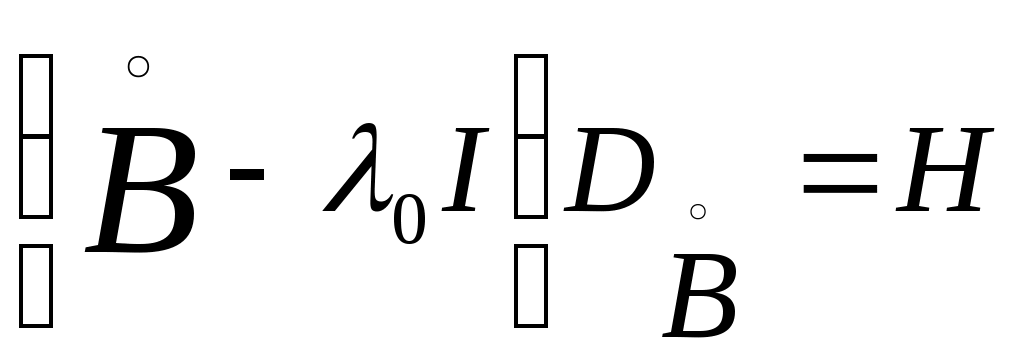 . .
Оператор 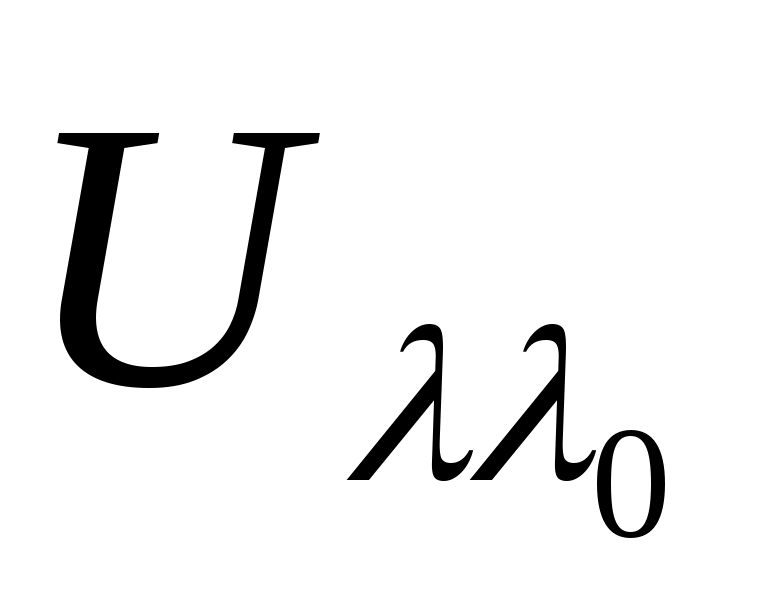 определяется формулами определяется формулами
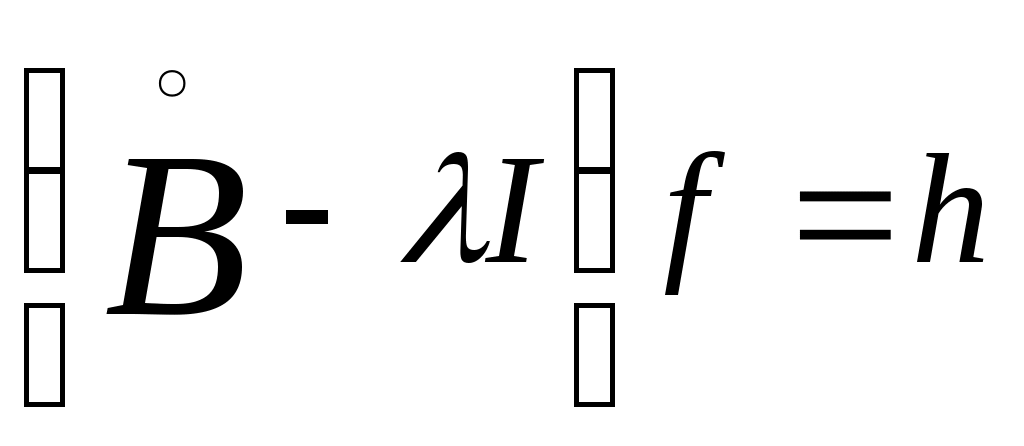 , , 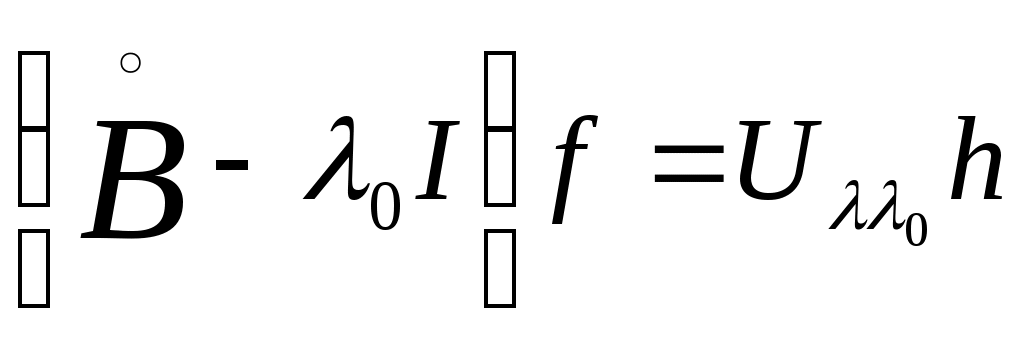 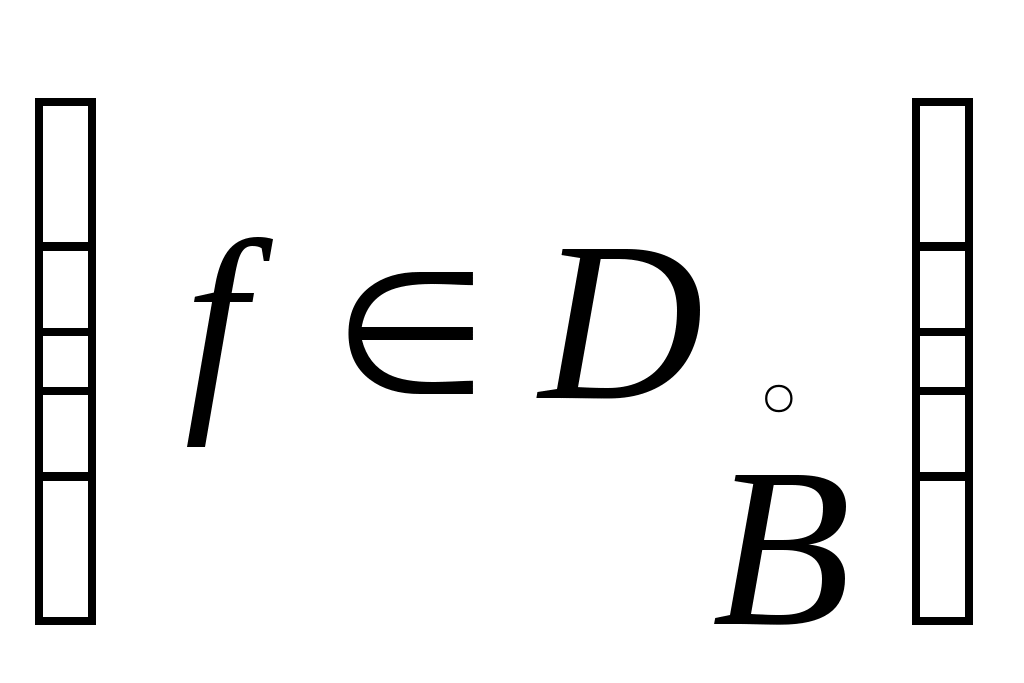 , ,
из которых следует, что осуществляемое им отображение Н на Н взаимно однозначно.
В частном случае, при 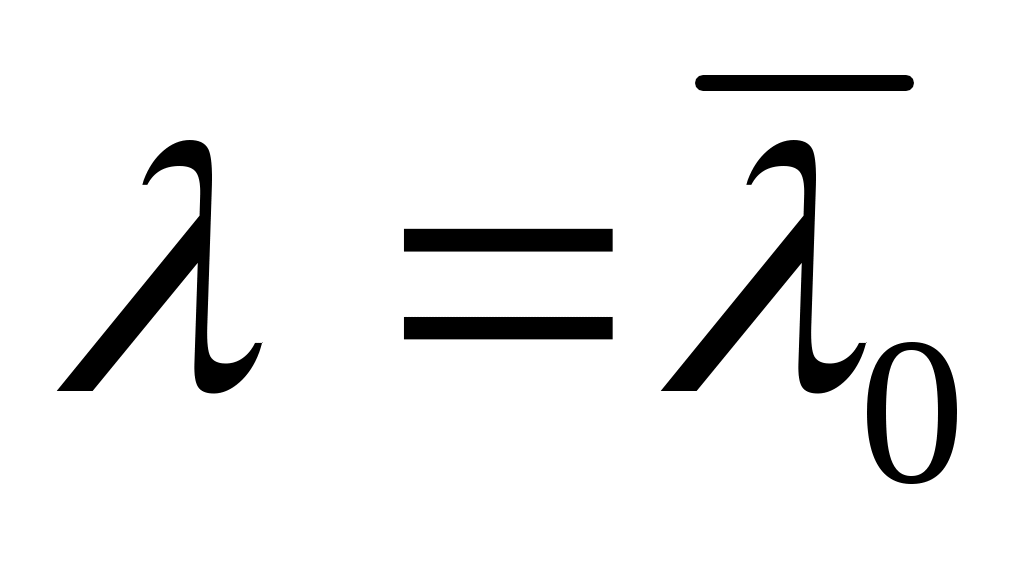 оператор оператор 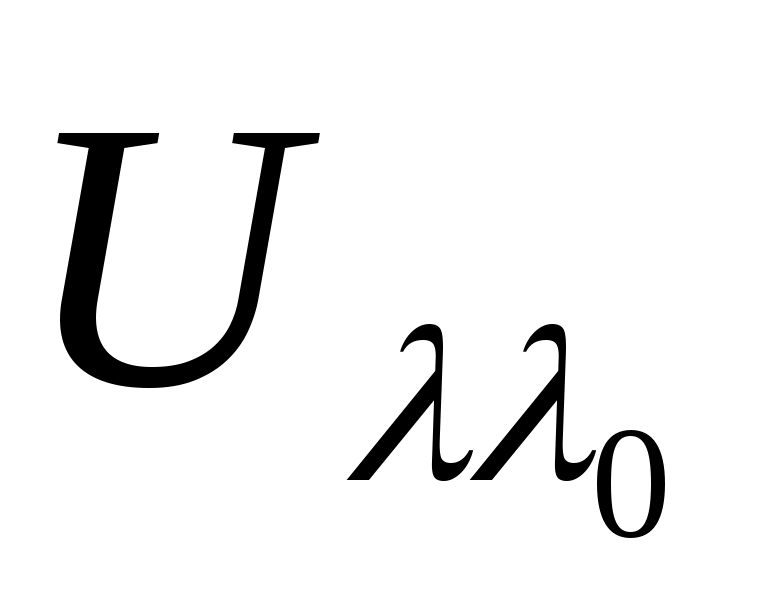 приводит к преобразованию Кэли оператора приводит к преобразованию Кэли оператора 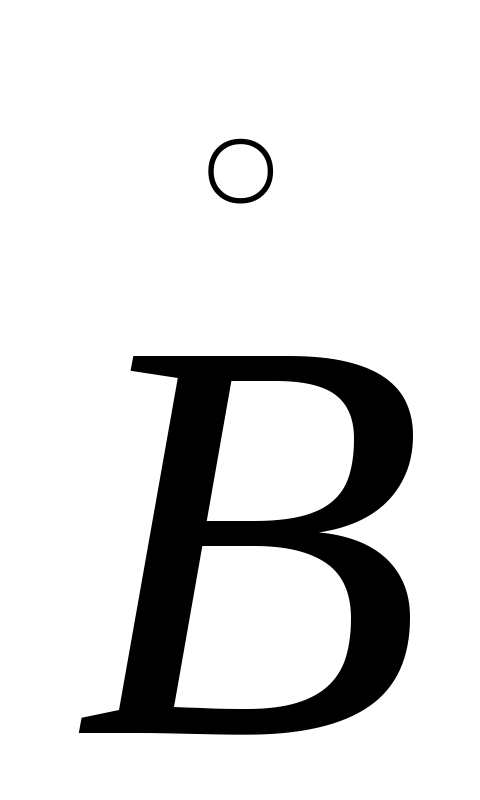 и отображает дефектное подпространство и отображает дефектное подпространство 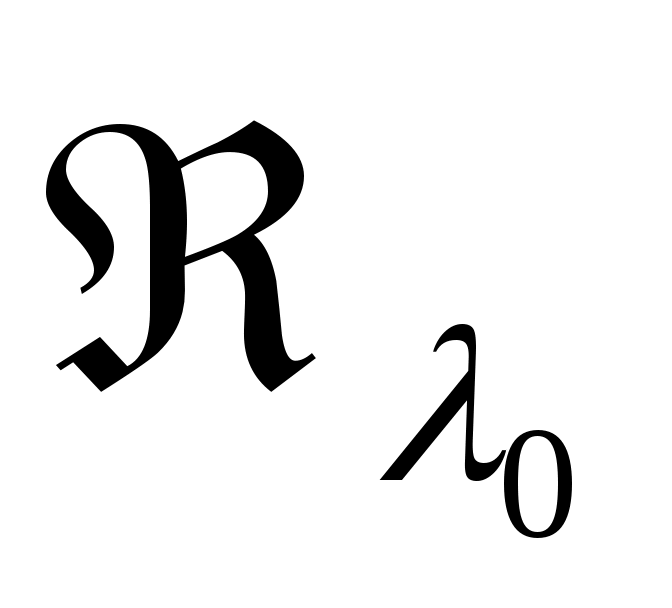 . Покажем, что вообще . Покажем, что вообще 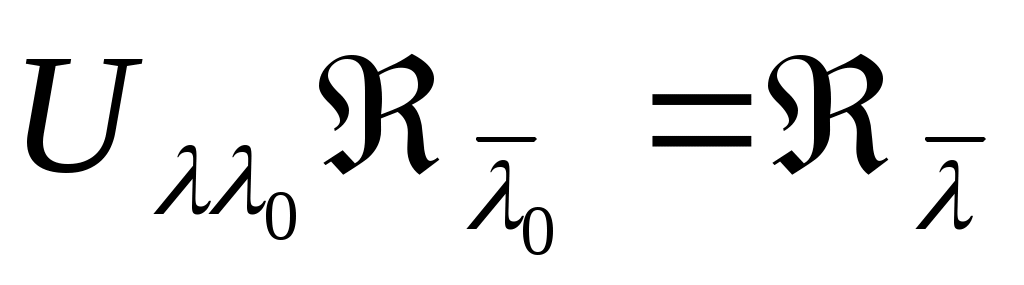 . .
Выберем произвольный базис 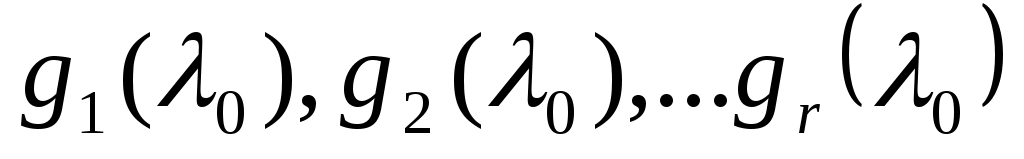 и докажем, что и докажем, что 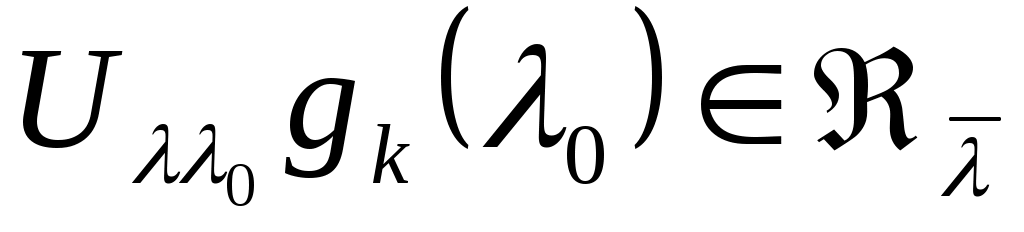 . .
Имеем
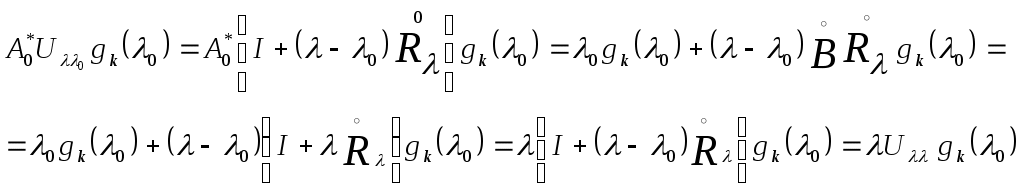
т.е. 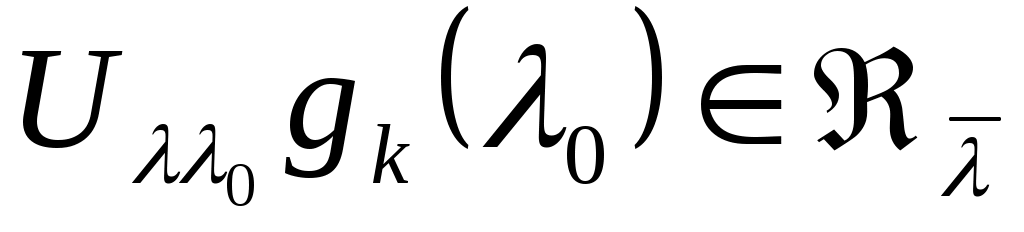 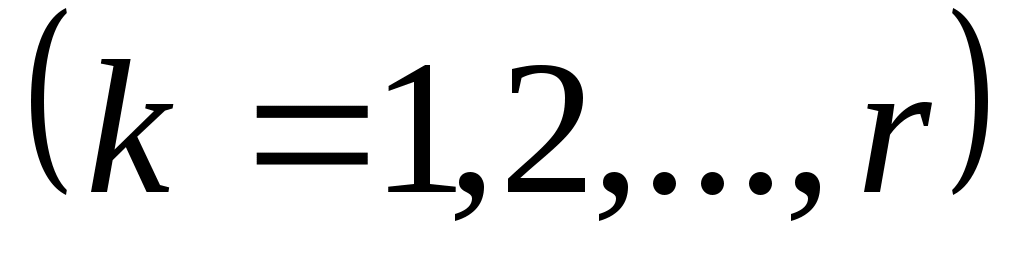 . При этом в силу взаимной однозначности отображения, осуществляемого оператором . При этом в силу взаимной однозначности отображения, осуществляемого оператором 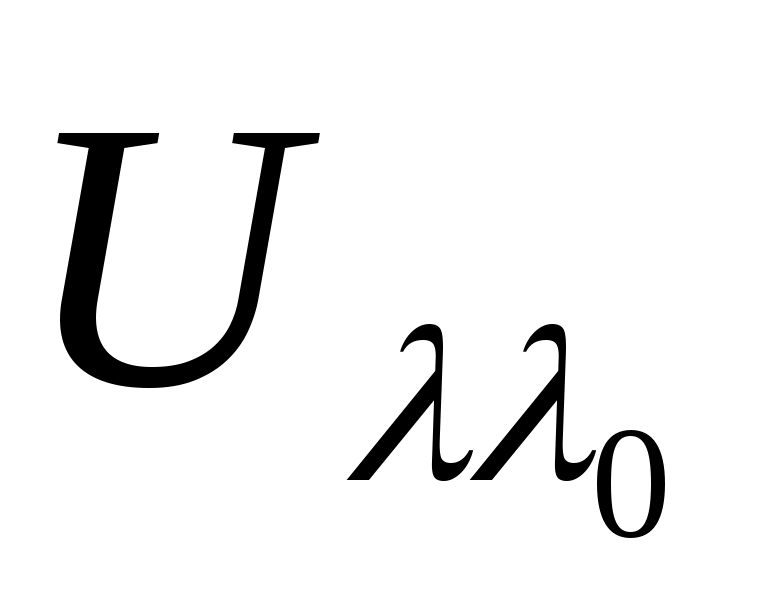 , векторы , векторы 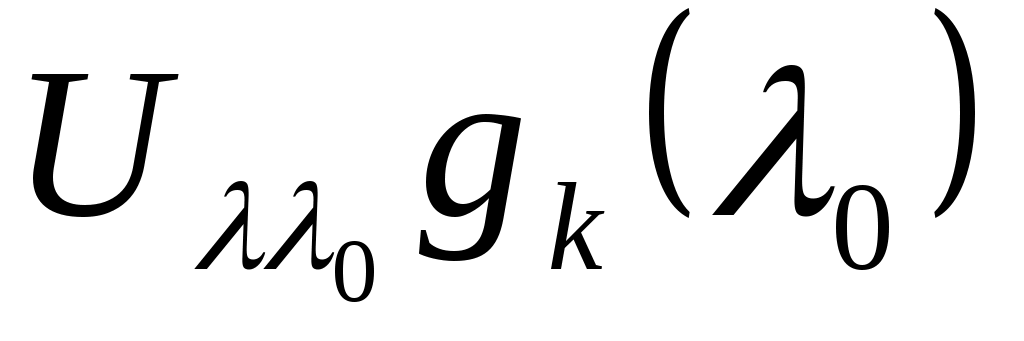 образуют базис в образуют базис в 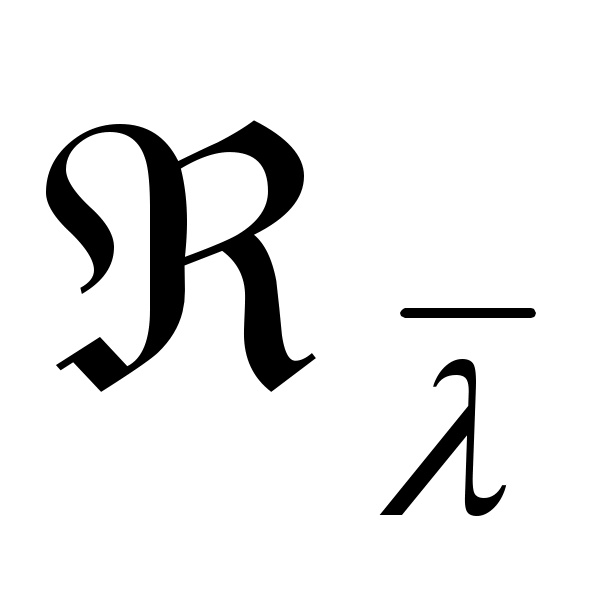 , и мы можем принять, что векторы , и мы можем принять, что векторы 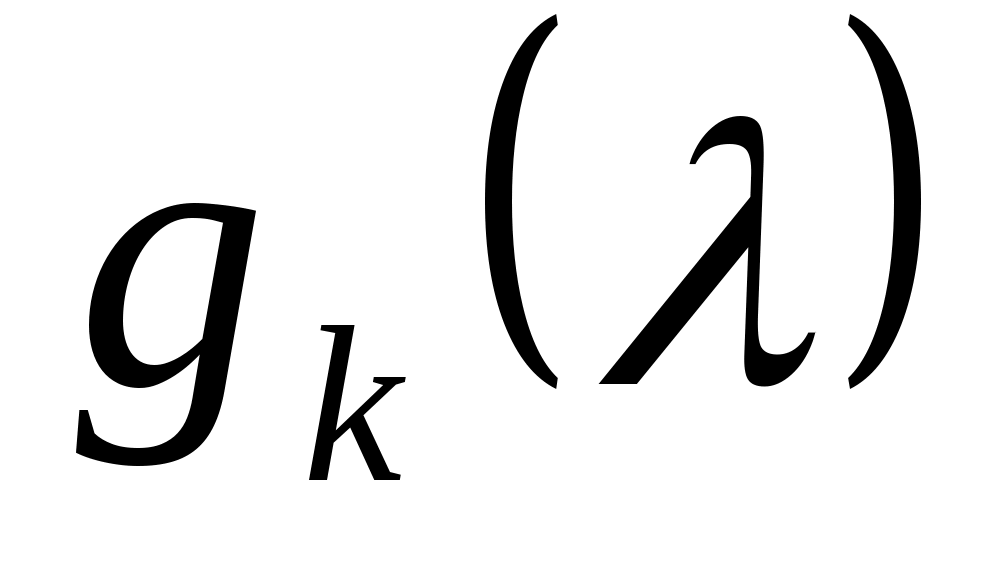 в любой точке регулярности оператора в любой точке регулярности оператора |
 Скачать 1.1 Mb.
Скачать 1.1 Mb.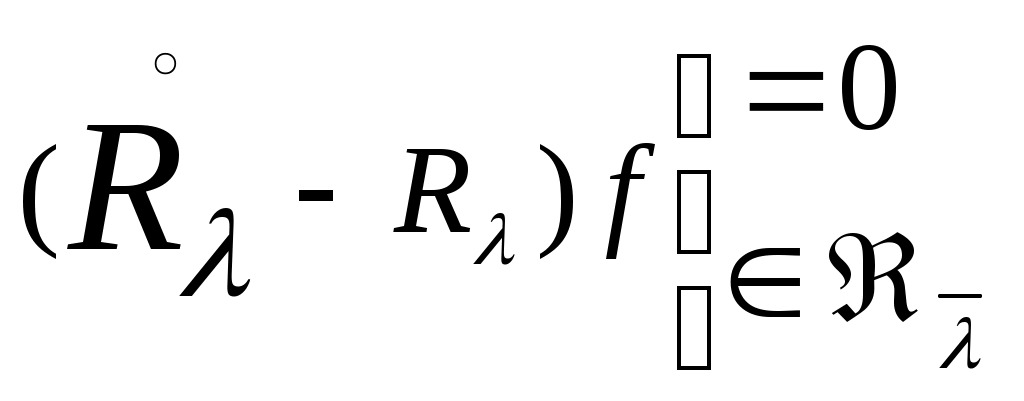
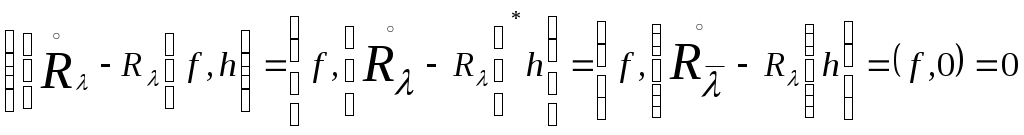 .
.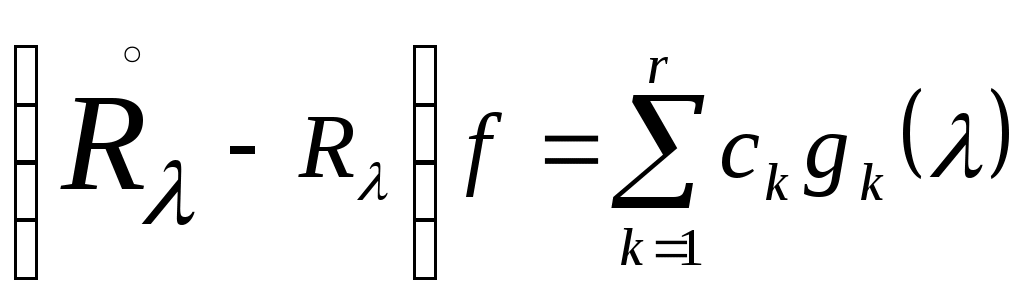 . (6)
. (6)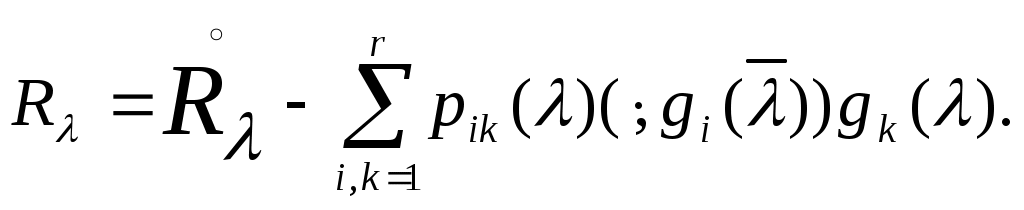 (9)
(9)