Чтобы получить симметрическое расширение заданного оператора а нужно найти изометрическое расширение его преобразования Кэли V
 Скачать 1.1 Mb.
|
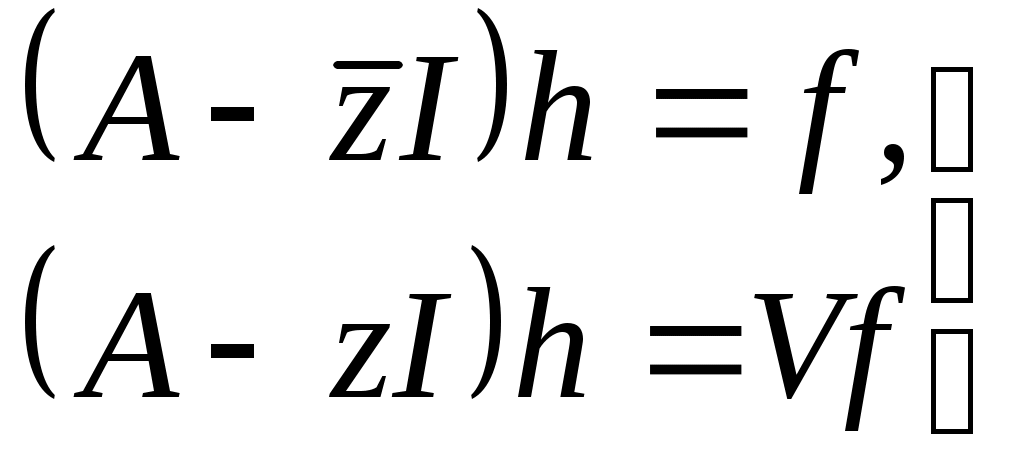 . Тогда  (1)- преобразование Кэли  замкнутого симметрического оператора  . Оператор выражается через оператор формулой  . При этом областью определения  оператора является  .В силу формул (1) 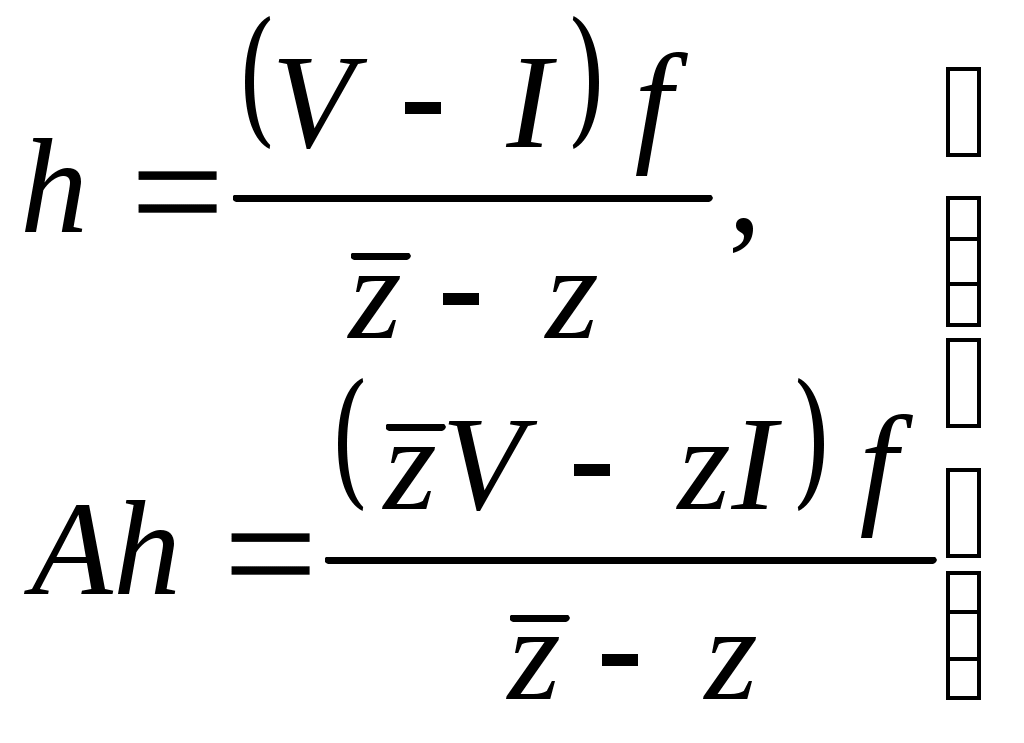 (2) и поэтому  . (2’)Утверждение. Индексы дефекта  оператора совпадают с индексами дефекта оператора .Действительно, по определению,  . Но  , следовательно,  . С другой стороны, снова по определению,  и  , так что  .Теорема 1. Если оператор V – изометрический и многообразие  плотно в Н, то определяемый формулой (2’) оператор А – симметрический, а оператор V есть его преобразование Кэли.Теорема 2. Пусть А1 и А2 – симметрические операторы, а V1 и V2 – их преобразования Кэли. Для того чтобы оператор А2 был расширением оператора А1, необходимо и достаточно, чтобы оператор V2 был расширением оператора V1. Таким образом теорема 2 сводит вопрос о симметрических расширениях заданного оператора А к вопросу об изометрических расширениях его преобразования Кэли. Известно, что замкнутые линейные многообразия F и G могут служить соответственно областью определения и изменения изометрического оператора тогда и только тогда, когда равны их размерности, тогда изометрические расширения оператора V могут быть получены следующим образом. Выберем в дефектных подпространствах  ,  два подпространства, F и G, равных размерностей и построим произвольный изометрический оператор V1 c областью определения F и областью значений G.Определим, далее, линейный оператор  с областью определения  и областью значений  формулами п  ри  .Очевидно, есть изометрическое расширение V и при всевозможных изменениях F, G, V1 мы получим все изометрические расширения оператора V и каждое по одному разу.Из приведенных выше рассуждений следует, в частности, что оператор А является максимальным симметрическим (самосопряженным) тогда и только тогда, когда его преобразование Кэли V является максимальным изометрическим оператором. Поэтому имеют место следующие теоремы. Теорема 3. Для того чтобы симметрический оператор был максимальным, необходимо и достаточно, чтобы одно из его дефектных чисел равнялось нулю. Для того чтобы симметрический оператор был самосопряженным, необходимо и достаточно, чтобы оба его дефектных числа равнялись нулю. Теорема 4. Пусть А – произвольный симметрический оператор с индексами дефекта . Оператор А всегда можно расширить до максимального. Если  , то среди таких расширений нет самосопряженных; если  и  ,  конечны, то любое максимальное расширение оператора А является самосопряженным; если же дефектные числа , бесконечны и равны, то среди максимальных расширений имеются как самосопряженные, так и несамосопряженные. Теорема. Пусть А – произвольный симметрический оператор с областью определения DA, a  и  ( >0) – какая-нибудь пара его дефектных подпространств. Для области определения DA* оператора А* имеет место следующее определение в виде прямой суммы трех линейных многообразий:DA* = DA   Доказательство. Покажем, что любой элемент f из DA* представим в виде f = f0 + g  + g , (1)где f0  DA, gz  , g  ; при этом следует заметить, что вместе с (1) будет иметь место формула  . (1’)Пусть  . Разложим элемент  на составляющие в ортогональных подпространствах  и  : .но  ; поэтому  ,откуда заключаем, что  ,т.е.  или  .Для окончания доказательства теоремы осталось установить, что представление (1) каждого элемента единственно. Допуская противное, примем, что  . (2)Применяя к обеим частям этого равенства оператор А*, получаем  . (2’)Умножая далее (2) на z и вычитая из (2’), получаем  ,откуда, вследствие ортогональности слагаемых, следует, что  ; точно также получим, что  ; следовательно,  .Теорема доказана. Найдем теперь  при любом . В соответствии с (1) и (1’), имеем  , где  , и .Так как сумма первых трех слагаемых вещественна, то  ,где в квадратных скобках снова стоит вещественная величина, а потому окончательно находим  . (3)В соответствии с формулой (3) область DA* состоит из трех (нелинейных) многообразий Г+ (совокупность элементов f, для которых  , Г- ((совокупность элементов f, для которых  вещественно). Элемент  принадлежит Г+, Г- или Г0, смотря потому, будет ли  или  (если ).Найдем теперь для области определения  любого симметрического расширения  оператора А представление, аналогичное формуле (1).Чтобы подчеркнуть зависимость подпространств F и G от z, будем писать Fz и Gz. Таким образом,  . или, полагая V1= - V',  .Из  следует, что при   (4)будет  . (4')Формулы (1) и (4) будем называть соответственно первой и второй формулой Неймана. Из первой формулы Неймана непосредственно следует для размерности DA* по модулю DA формула:  . (5)Вторая формула Неймана совместно с равенством (4’) описывает все симметрические расширения  заданного оператора А. Если, в частности, оператор А имеет равные дефектные числа и есть его самосопряженное расширение, то в формуле (4) элемент  будет пробегать все подпространство  , а  - все . Обратно, если в (4) элемент пробегает все , а  - все , то оператор будет самосопряженным расширением оператора А. Если индексы дефекта оператора А и его симметрического расширения суть (m, n) и (m-p, n-p), где  , то из второй формулы Неймана вытекает соотношение 3. ФОРМУЛА КРЕЙНА ДЛЯ РЕЗОЛЬВЕНТ САМОСОПРЯЖЕННЫХ РАСШИРЕНИЙ ЗАДАННОГО СИММЕТРИЧЕСКОГО ОПЕРАТОРА Теорема 1. Все самосопряженные расширения оператора с равными и конечными дефектными числами имеют один и тот же непрерывный спектр. Теорема 2. При произвольном расширении оператора с равными и конечными индексами дефекта ( , ) до самосопряженного оператора кратность собственных значений повышает не более чем на единиц (в частности, новые собственные значения имеют кратность, не превосходящую ).Теорема3. Если  - вещественная точка регулярного типа симметрического оператора А с индексом дефекта  , то существует самосопряженное расширение оператора А, для которого число |