Чтобы получить симметрическое расширение заданного оператора а нужно найти изометрическое расширение его преобразования Кэли V
 Скачать 1.1 Mb.
|
 определены формулами  , и, следовательно, являются регулярными аналитическими вектор-функциями от  .С помощью функционального уравнения резольвенты легко проверить, что в таком случае для любых двух регулярных точек и  оператора имеют место равенства . (10)Теперь значение матричной функции  при любом (регулярном для и  ) определяется по ее значению  ; для нахождения соответствующей формулы воспользуемся функциональным уравнением резольвенты . (11)С другой стороны, в силу (7) 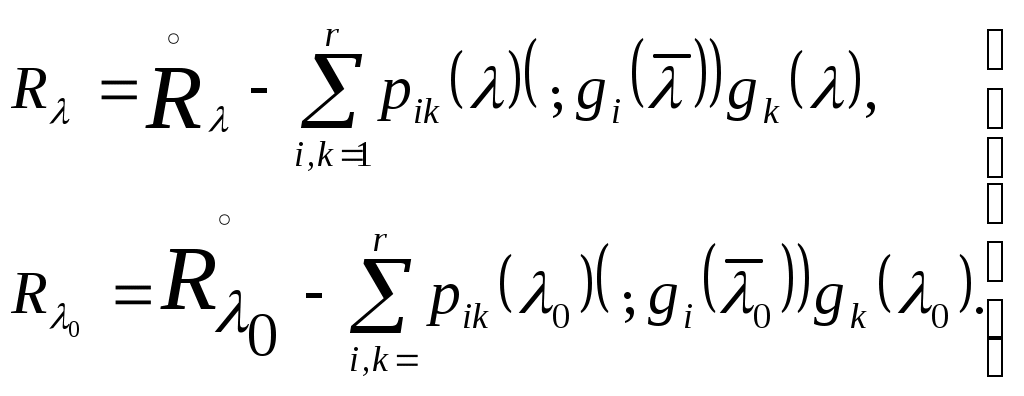 (12)Подставляя правые части (12) в (11), получаем (13): 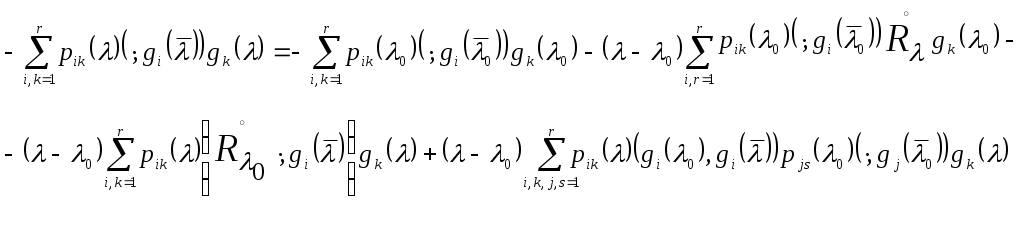 Если с помощью (10) приведем сумму второго и третьего слагаемого в правой части к виду  ,и после этого приведем в (13) подобные члены, то получим 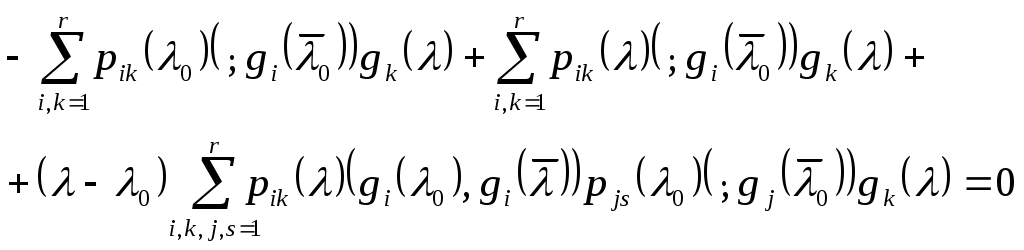 Отсюда, в силу линейной независимости векторов  , и, далее, в силу линейной независимости   или, в матричном виде,  .Умножая последнее равенство справа на  и слева на  , получаем искомое соотношение (14)Нетрудно проверить, что из (14) для любых двух общих регулярных точек и операторов , следует .пространство симметрический оператор СПИСОК ИСПОЛЬЗУЕМЫХ ИСТОЧНИКОВ Н.И. Ахиезер, И.М. Глазман. Теория линейных операторов в гильбертовом пространстве. – М., 1966. – 544 с. Треногин В.А. Функциональный анализ: Учебник. – 4-е изд., испр. – М. ФИЗМАТЛИТ, 2007. – 488с. Хатсон В., Пим Дж. С. Приложения функционального анализа и теория операторов. Пер. с англ. – М.: Мир, 1983, 432 с. |