|
Размещено на http://www.allbest.ru/
СОДЕРЖАНИЕ
Введение
Индексы дефекта
Преобразование Кэли и формулы Неймана
Формула Крейна для резольвент самосопряженных расширений заданного симметрического оператора
Литература
ВВЕДЕНИЕ
Чтобы получить симметрическое расширение заданного оператора А нужно найти изометрическое расширение его преобразования Кэли V. Для этого выберем в дефектных подпространствах 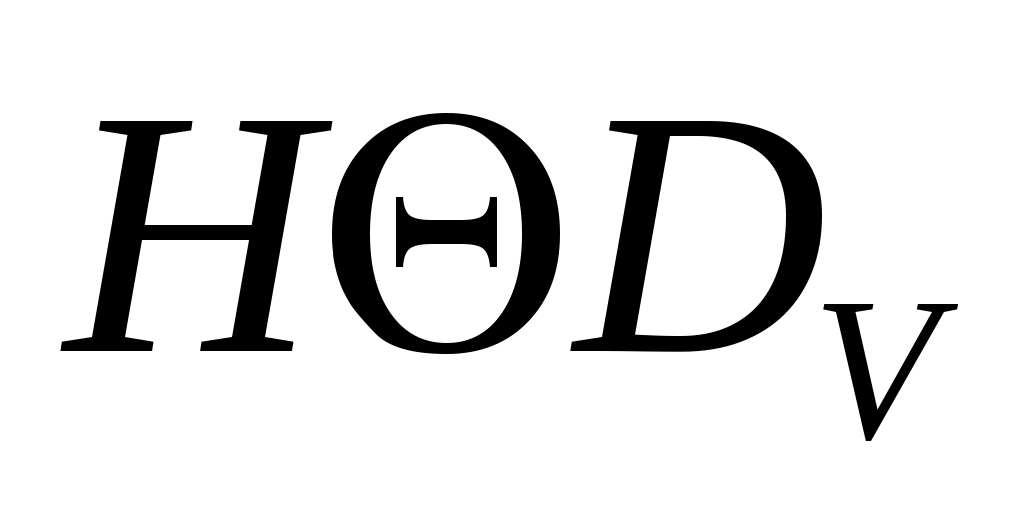 , ,  два подпространства, F и G, равных размерностей и построим произвольный изометрический оператор V1 c областью определения F и областью значений G. два подпространства, F и G, равных размерностей и построим произвольный изометрический оператор V1 c областью определения F и областью значений G.
Определим, далее, линейный оператор  с областью определения с областью определения 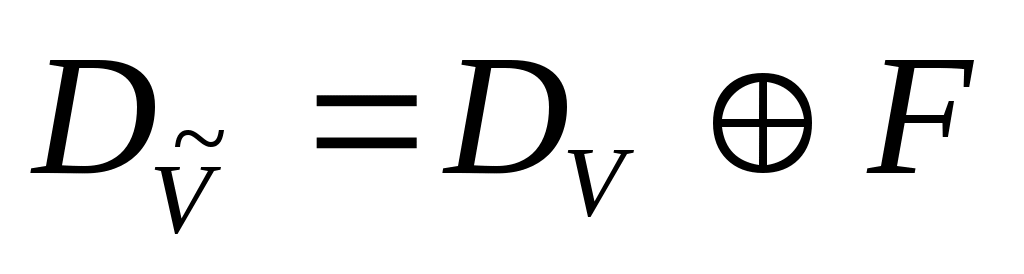 и областью значений и областью значений  формулами формулами
п ри ри  . .
Очевидно,  есть изометрическое расширение V и при всевозможных изменениях F, G, V1 мы получим все изометрические расширения есть изометрическое расширение V и при всевозможных изменениях F, G, V1 мы получим все изометрические расширения  оператора V и каждое по одному разу. оператора V и каждое по одному разу.
Итак, чтобы найти некоторое симметрическое расширение  оператора А, следует перейти к преобразованию Кэли оператора А, найти по описанному выше методу некоторое расширение оператора А, следует перейти к преобразованию Кэли оператора А, найти по описанному выше методу некоторое расширение  оператора V и, наконец, вернуться к оператора V и, наконец, вернуться к  , выполнив преобразование Кэли над , выполнив преобразование Кэли над  . .
1. ИНДЕКСЫ ДЕФЕКТА
Определение: Всякую функцию  , которая каждому элементу , которая каждому элементу  относит некоторый элемент относит некоторый элемент  , называют оператором в пространстве Н с областью определения , называют оператором в пространстве Н с областью определения  и областью значений и областью значений  , состоящей из всех , состоящей из всех  , где , где  пробегает все пробегает все  . .
Тождественный оператор, т.е. оператор, переводящий каждый вектор сам в себя, будем обозначать  . Область определения и область значение оператора будем обозначать . Область определения и область значение оператора будем обозначать  , соответственно. , соответственно.
Если оператор  двум различным элементам из двум различным элементам из  относит различные элементы, то относит различные элементы, то  имеет обратный оператор, который элементам из имеет обратный оператор, который элементам из  относит элементы из относит элементы из  . Обратный оператор обозначают символом . Обратный оператор обозначают символом  , таким образом, , таким образом,
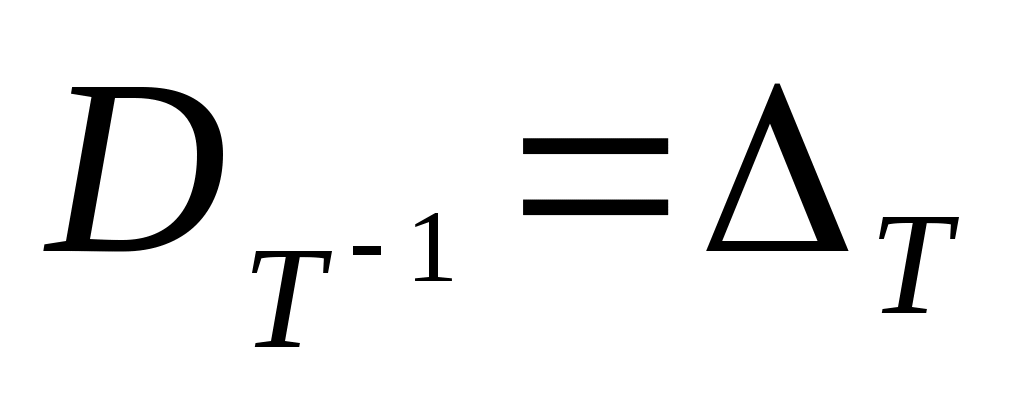 , ,  . .
Определение: Оператор  называется непрерывным в точке называется непрерывным в точке  ( ( ), если ), если 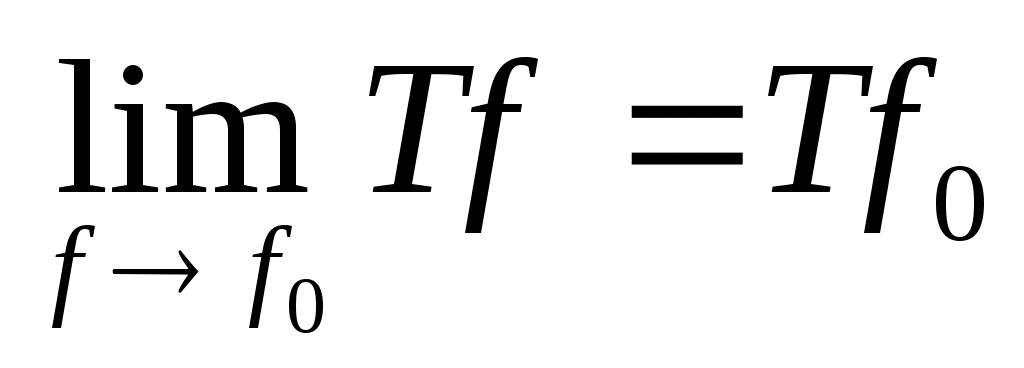 ( ( ); это означает, что при любом ); это означает, что при любом  существует такое существует такое 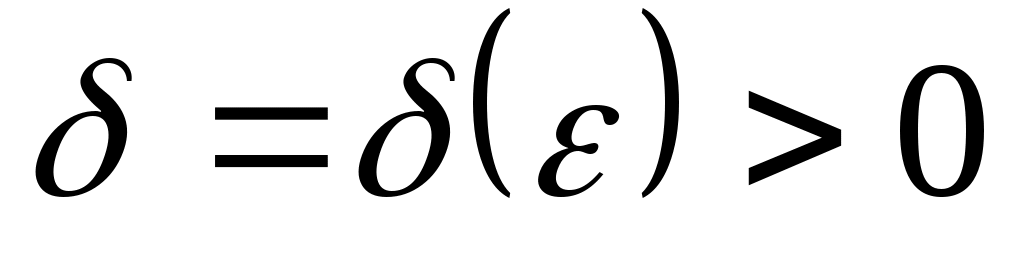 , что из , что из 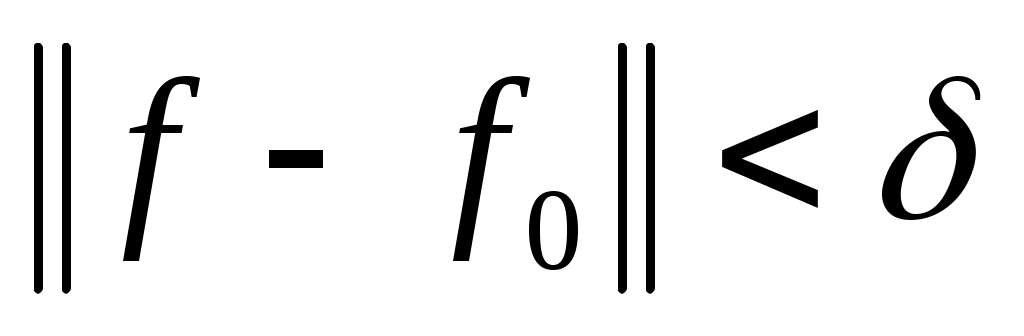 , ,   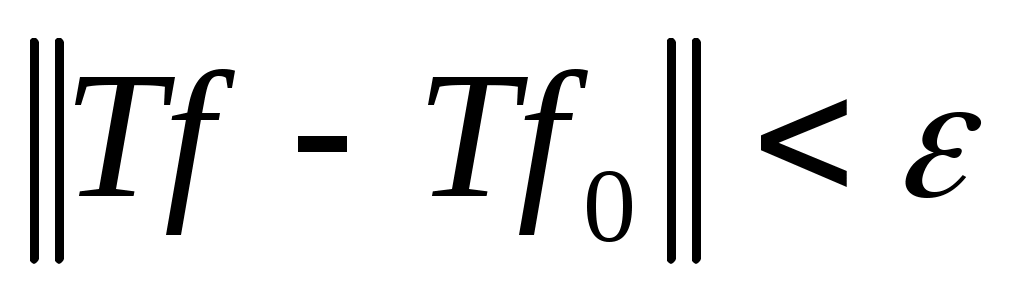 . .
Если область определения  оператора оператора  шире области определения шире области определения  оператора оператора  , т.е. , т.е. 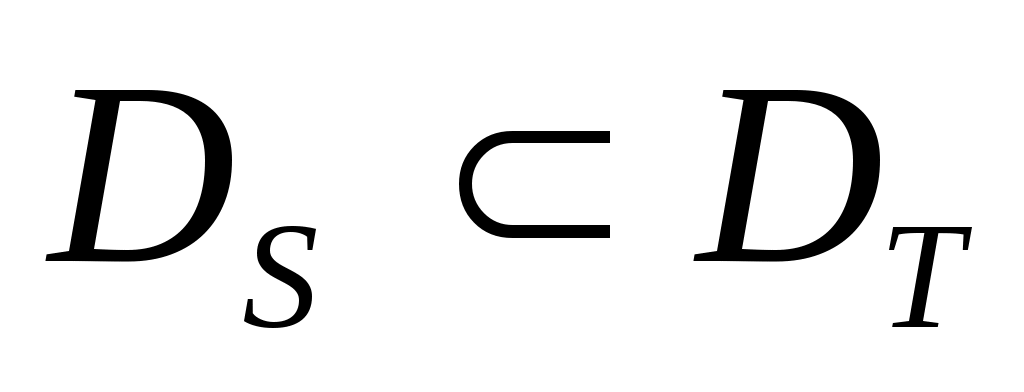 , и если , и если  для любого элемента для любого элемента  , то оператор , то оператор  называют расширением оператора называют расширением оператора  ( (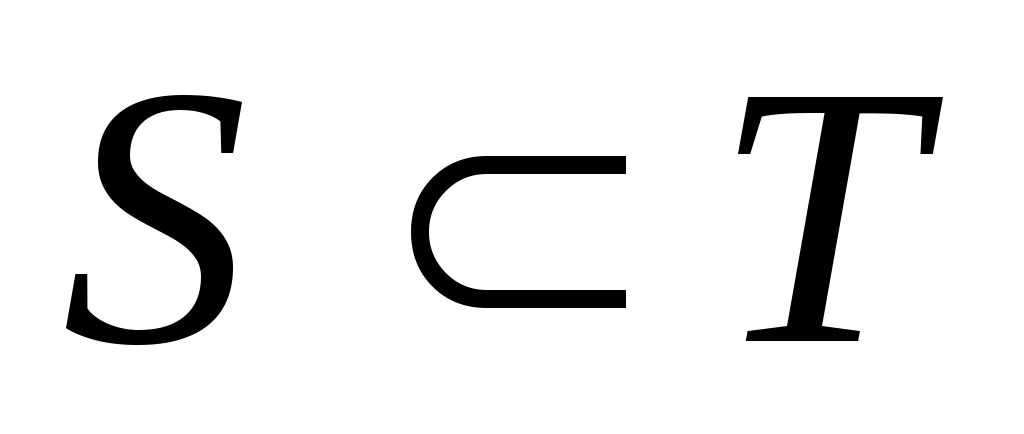 ). ).
Определение. Оператор Т называется линейным, если его область определения D есть линейное многообразие и  для любых для любых  и любых комплексных и любых комплексных 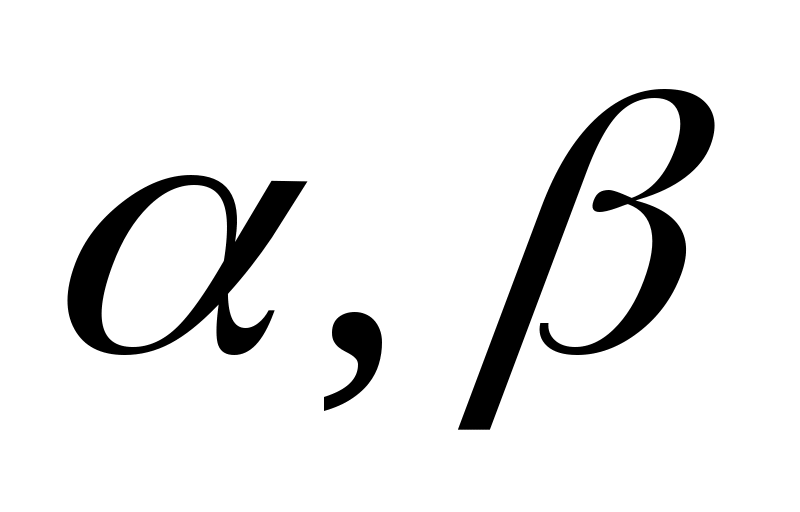 . .
Определение. Оператор V, заданный на всем пространстве Н1(DV=H1) и отображающий его на все пространство Н2 ( ), называется изометрическим, если для любых ), называется изометрическим, если для любых 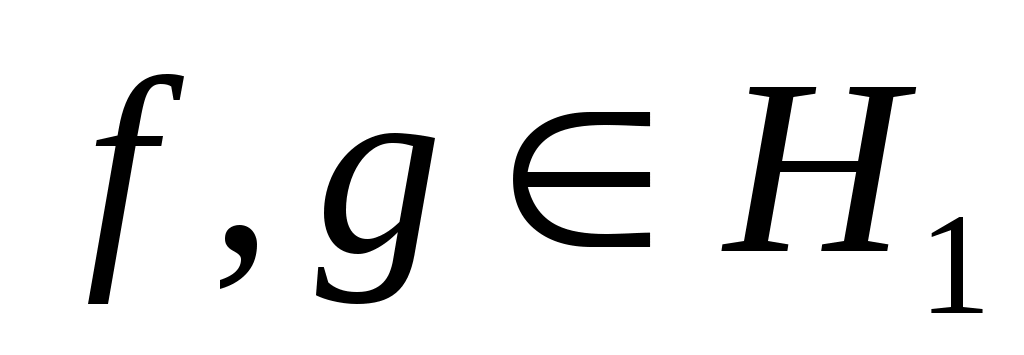 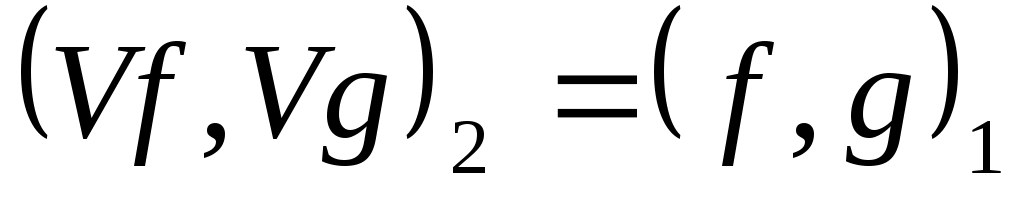 . .
Определение. Линейный оператор А называется симметрическим, если
область определения DA плотна в Н и
для любых двух элементов f, g из DA имеет место равенство 
Определение. Значения параметра  , для которых обратный оператор , для которых обратный оператор  существует, определен всюду в существует, определен всюду в 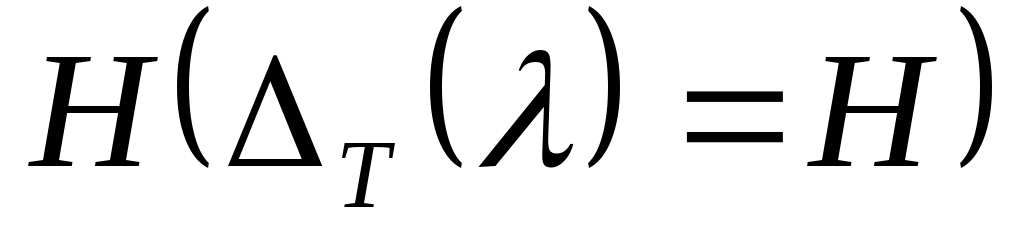 и ограничен, называют регулярными значениями оператора Т. Все остальные точки комплексной плоскости образуют спектр оператора Т. и ограничен, называют регулярными значениями оператора Т. Все остальные точки комплексной плоскости образуют спектр оператора Т.
Определение. Резольвентой оператора Т называют зависящий от параметра  оператор оператор 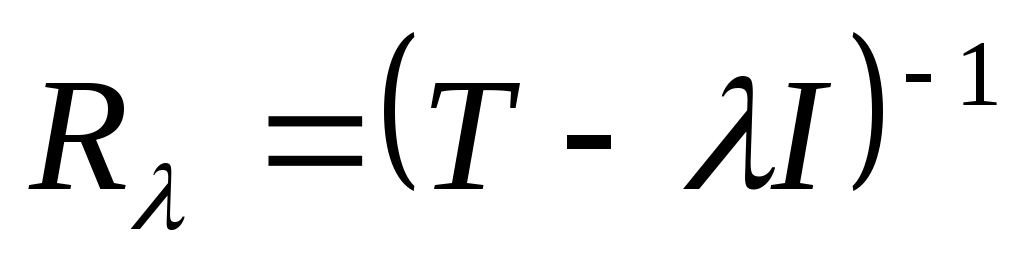 , рассматриваемый на множестве всех тех значений , рассматриваемый на множестве всех тех значений  , для которых он существует и для которых его область определения, т.е. , для которых он существует и для которых его область определения, т.е. 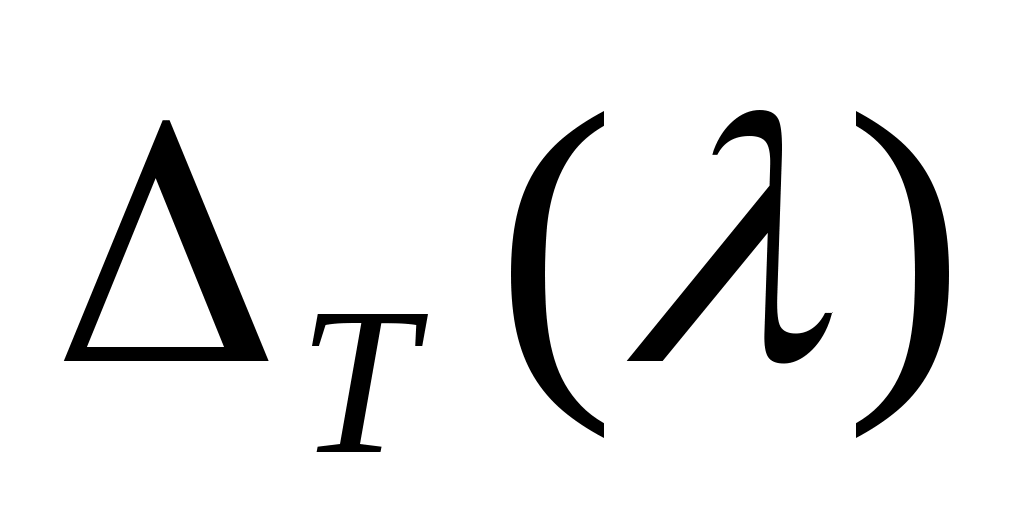 плотна в Н. плотна в Н.
Пусть  - произвольный линейный оператор. - произвольный линейный оператор.
Определение: число  назовем точкой регулярного типа оператора назовем точкой регулярного типа оператора  , если существует такое , если существует такое 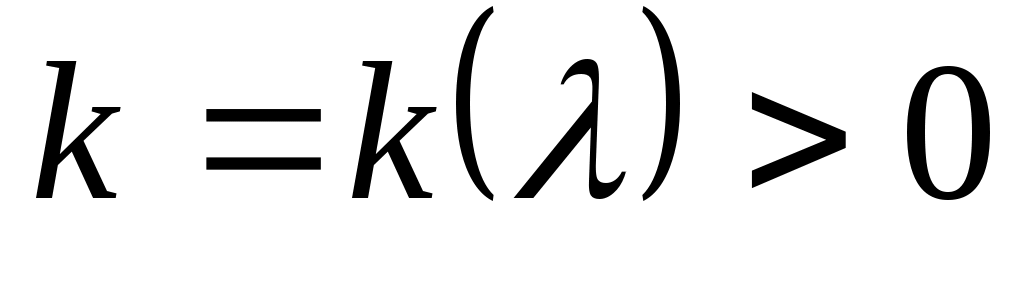 , что при всех , что при всех 
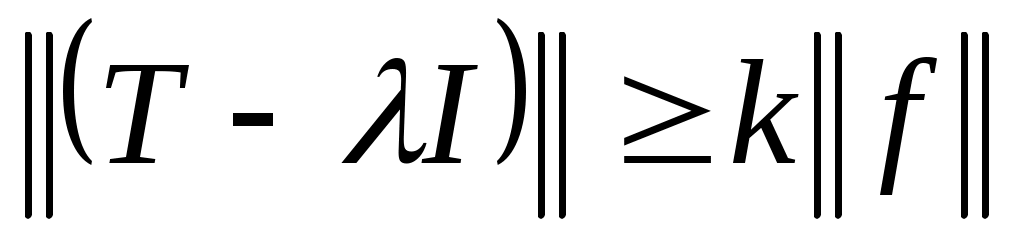 . .
Поэтому собственные значения оператора  не являются для него точками регулярного типа. не являются для него точками регулярного типа.
Если  точка регулярного типа оператора точка регулярного типа оператора  , то оператор , то оператор  существует и ограничен, и обратно, если оператор существует и ограничен, и обратно, если оператор  существует и ограничен, то существует и ограничен, то  есть точка регулярного типа. есть точка регулярного типа.
Если  есть точка регулярного типа, то при есть точка регулярного типа, то при  и любом и любом  имеет место неравенство имеет место неравенство
 . .
Оно показывает, что множество точек регулярного типа всегда открыто. Это множество точек называется полем регулярности оператора  . .
Если  есть симметрический оператор и есть симметрический оператор и   , то при любом , то при любом 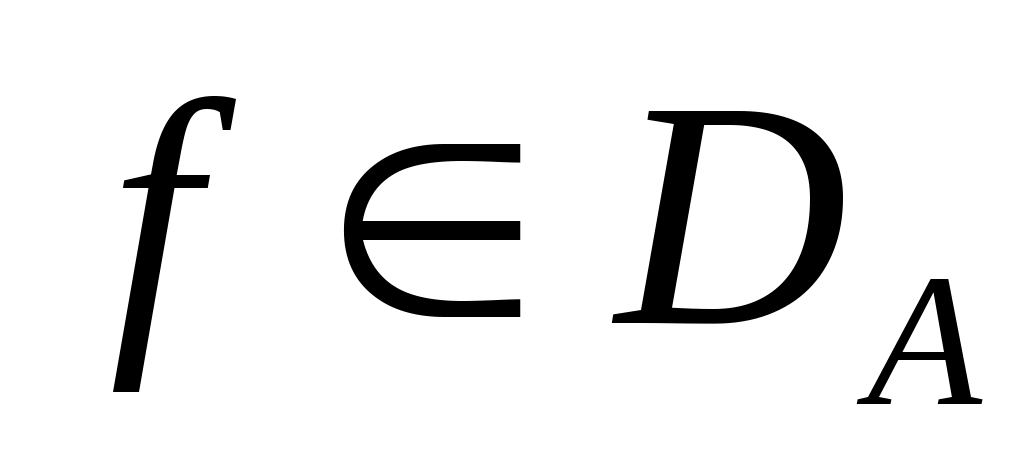
 . .
Отсюда видно, что верхняя и нижняя половины  -плоскости являются связными компонентами поля регулярности любого симметрического оператора. -плоскости являются связными компонентами поля регулярности любого симметрического оператора.
Теорема: если  есть связная компонента поля регулярности линейного оператора есть связная компонента поля регулярности линейного оператора  , то размерность подпространства , то размерность подпространства  одинакова для всех одинакова для всех 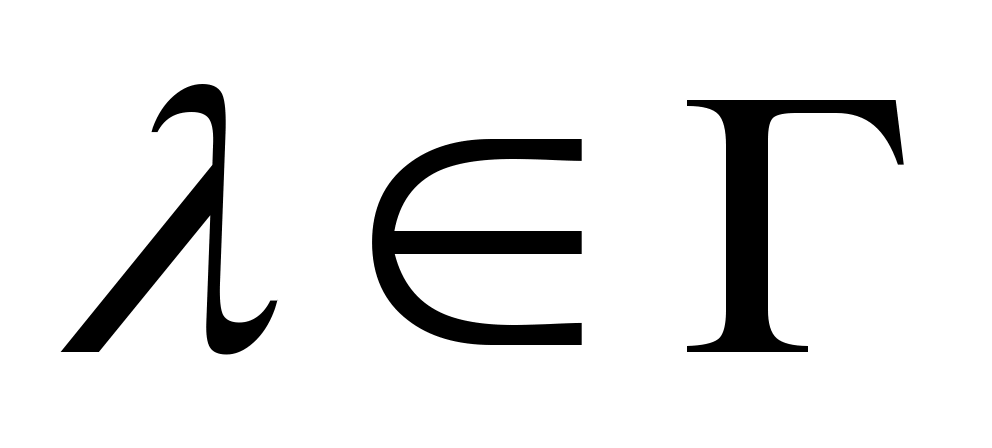 . .
Условимся называть дефектным числом линейного многообразия  размерность его ортогонального дополнения размерность его ортогонального дополнения  и будем писать и будем писать
 . .
Определение: дефектное число линейного многообразия 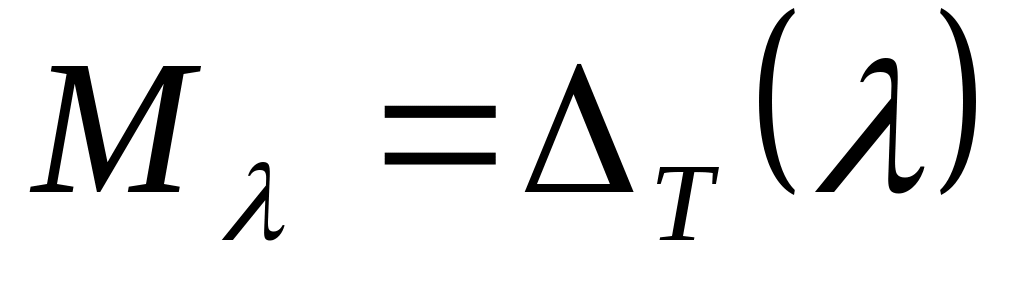 для точек для точек  , принадлежащих данной связной компоненте поля регулярного оператора , принадлежащих данной связной компоненте поля регулярного оператора  , называется дефектным числом оператора , называется дефектным числом оператора  в этой компоненте поля регулярности. При этом в этой компоненте поля регулярности. При этом  называется дефектным подпространством оператора называется дефектным подпространством оператора  для точки для точки  , а любой отличный от нуля элемент дефектного подпространства называется дефектным элементом. , а любой отличный от нуля элемент дефектного подпространства называется дефектным элементом.
Каждый симметрический оператор  имеет два дефектных числа, а именно одно ( имеет два дефектных числа, а именно одно ( ) в нижней, другое ( ) в нижней, другое ( ) в верхней полуплоскости. Их называют также индексами дефекта оператора ) в верхней полуплоскости. Их называют также индексами дефекта оператора  : :
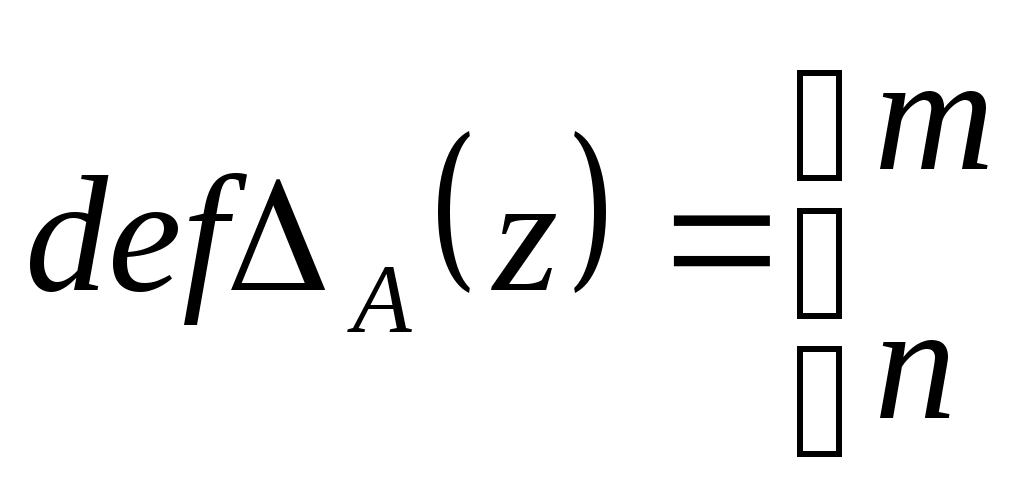 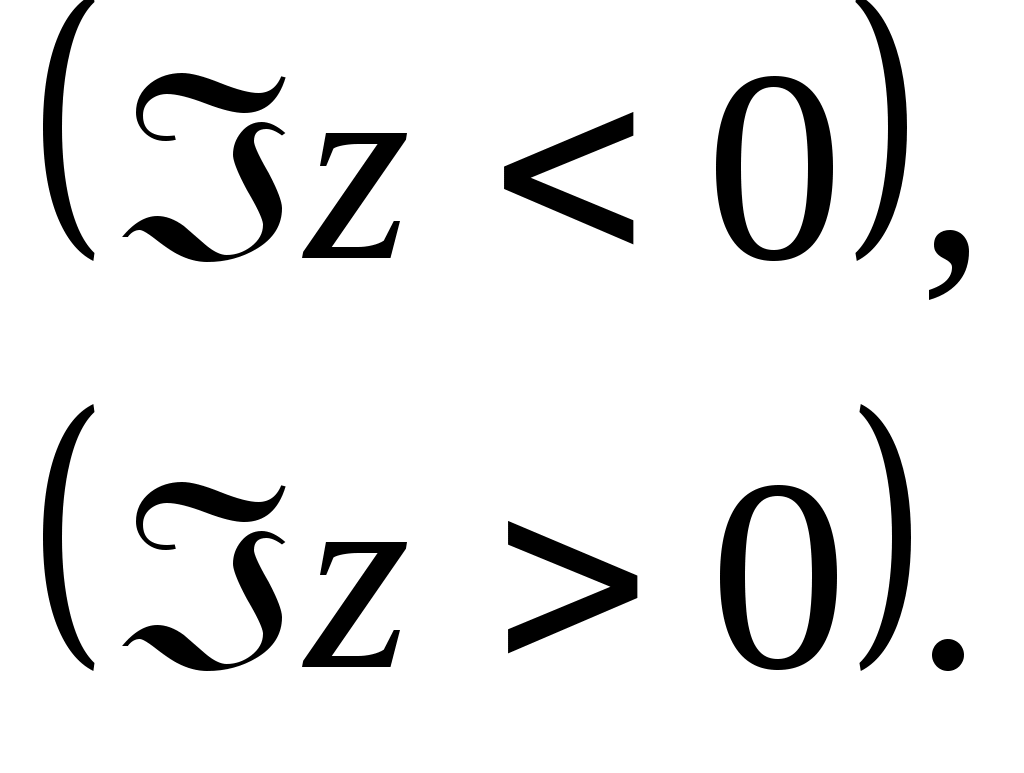
Индексы дефекта симметрического оператора образуют упорядоченную пару чисел  . .
Из приведенной выше теоремы вытекают следующие три предложения.
1°. Если симметрический оператор имеет вещественную точку регулярного типа, то его дефектные числа равны: 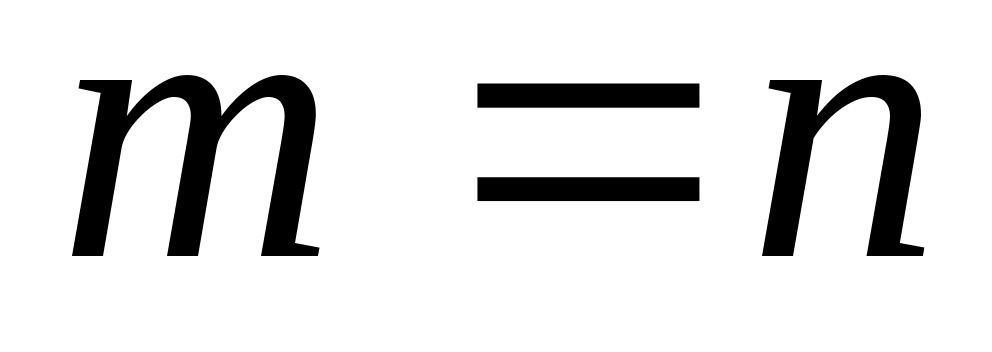 . То же справедливо относительно изометрического оператора, если он имеет точку регулярного типа на единичной окружности. . То же справедливо относительно изометрического оператора, если он имеет точку регулярного типа на единичной окружности.
2°. Если  - симметрический оператор, то любое невещественное число - симметрический оператор, то любое невещественное число  является для сопряженного оператора является для сопряженного оператора  собственным значением: кратности собственным значением: кратности  , если , если  , и кратности , и кратности  , если , если  . .
3°. Дефектные числа изометрического оператора 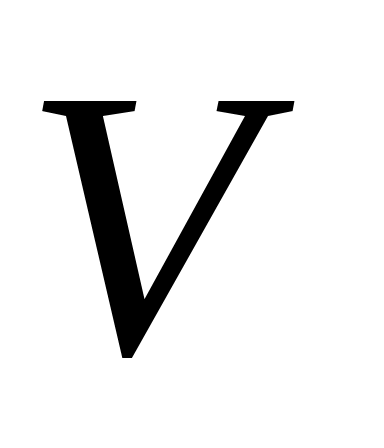 могут быть определены с помощью следующих равенств: могут быть определены с помощью следующих равенств:
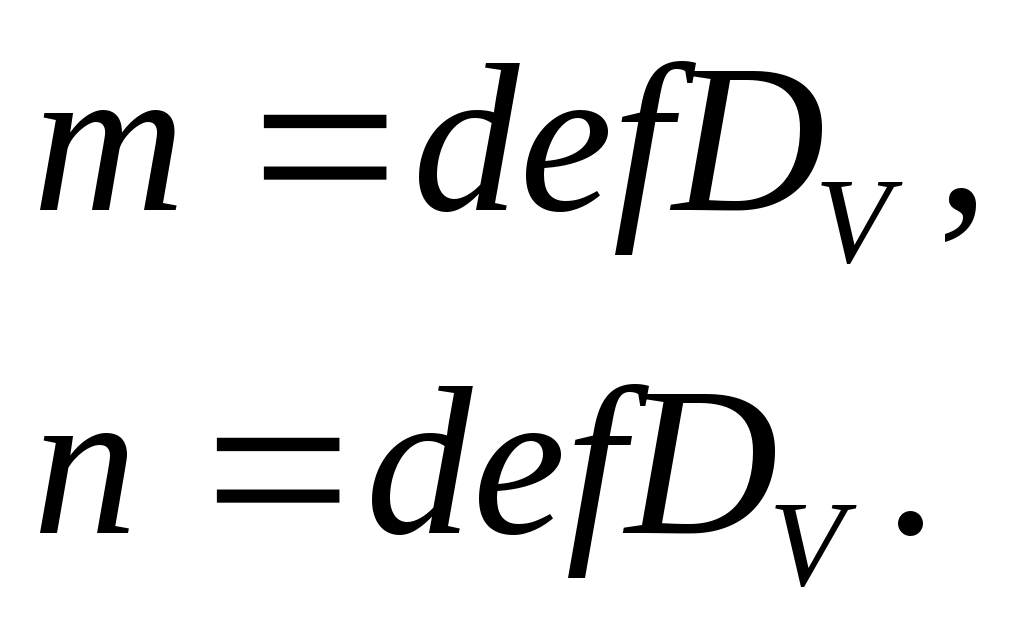
2. ПРЕОБРАЗОВАНИЕ КЭЛИ И ФОРМУЛЫ НЕЙМАНА
Пусть  - какое-нибудь вещественное число, а - какое-нибудь вещественное число, а  пробегает пробегает 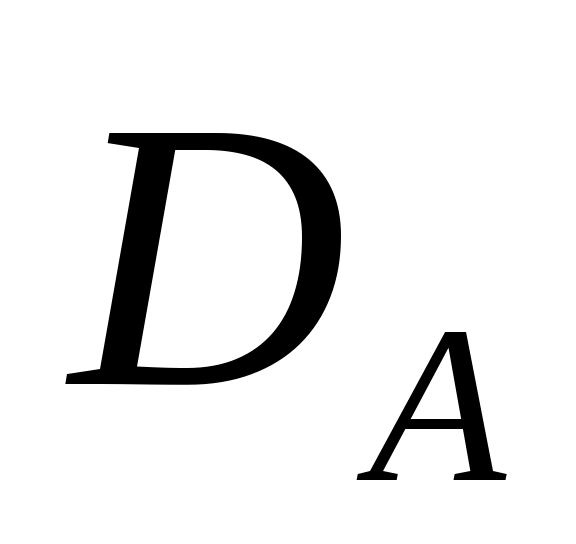 . Будем полагать, что . Будем полагать, что |
 Скачать 1.1 Mb.
Скачать 1.1 Mb. ри
ри