презентация на тему счисления чисел. Презинтация''Система счисления''. Цифры это знаки, используемые при записи чисел. Сами знаки составляют алфавит
 Скачать 1.18 Mb. Скачать 1.18 Mb.
|
  Система счисления — это знаковая система, в которой числа записываются по определенным правилам с помощью символов некоторого алфавита, называемых цифрами. Цифры – это знаки, используемые при записи чисел. Сами знаки составляют алфавит системы счисления. 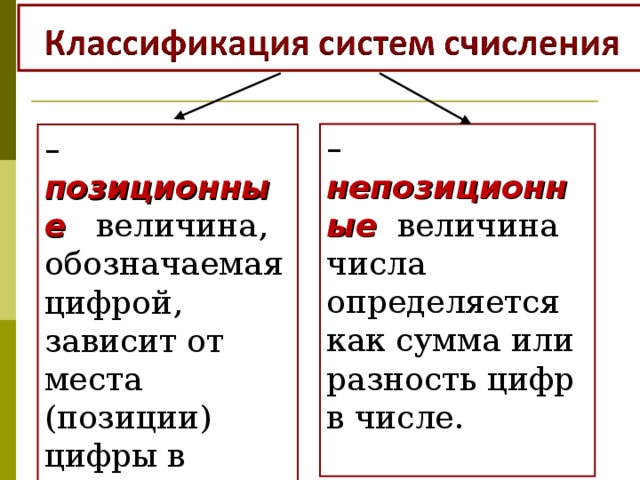 – непозиционные величина числа определяется как сумма или разность цифр в числе. – позиционные величина, обозначаемая цифрой, зависит от места (позиции) цифры в числе ; НЕПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ Алфавит системы содержит неограниченное количество символов. Единичная ("палочная ”, “ унарная ” ) система счисления Потребность в записи чисел появилась в очень древние времена, как только люди начали считать. Количество предметов изображалось нанесением чёрточек или засечек на какой - либо твёрдой поверхности: камне, глине, дереве (до изобретения бумаги было ещё очень и очень далеко). Каждому объекту в такой записи соответствовала одна чёрточка. Археологами найдены такие "записи" при раскопках культурных слоёв, относящихся к периоду палеолита (10 - 11 тысяч лет до н.э.). Учёные назвали этот способ записи чисел единичной ("палочной") системой счисления. В ней для записи чисел применялся только один вид знаков - "палочка". Каждое число в такой системе счисления обозначалось с помощью строки, составленной из палочек, количество которых и равнялось обозначаемому числу. Перуанцы употребляли для запоминания чисел разноцветные шнуры с завязанными на них узлами. Интересный способ для записи чисел использовался индийскими цивилизациями примерно в VIII веке до новой эры. Они применяли «узелковое письмо» - связанные между собой нити. Знаками на этих нитях служили узелки, часто с вплетенными в них камнями или ракушками. Узелковая запись чисел позволяла Инкам передавать информацию о числе воинов, обозначать количество умерших или родившихся в той или иной провинции и так далее. Около 1100 года н. э. английский король Генрих I изобрел одну из самых необычных денежных систем в истории, названную системой «мерных реек». Эта денежная система продержалась 726 лет и была отменена в 1826 году. Деревянная полированная рейка с зарубками, обозначающими номинал, расщеплялась по всей длине так, чтобы сохранить зарубки. Неудобства такой системы записи чисел и ограниченность её применения очевидны: чем большее число надо записать, тем длиннее строка из палочек. Да и при записи большого числа легко ошибиться, нанеся лишнее количество палочек или, наоборот, не дописав их.  ПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ Основание системы – это количество различных знаков, используемых для изображения чисел в данной системе. Троичная 0, 1, 2 Пятеричная 0, 1, 2, 3, 4 Следует помнить и не забывать, что первый разряд числа является нулевым. Двенадцатеричная 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B Позиция цифры в числе называется разрядом. 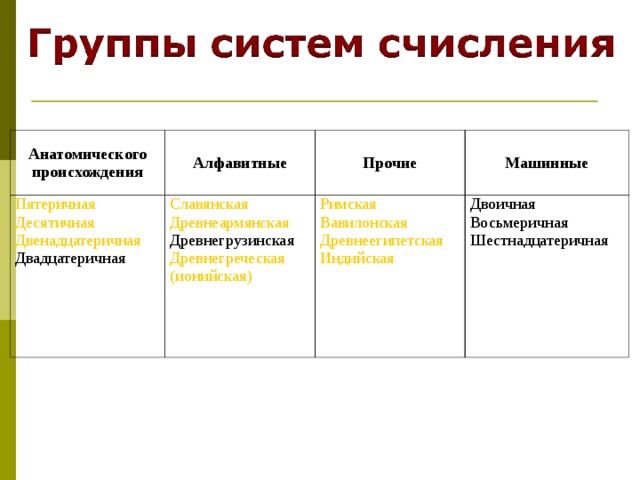 Анатомического происхождения Алфавитные Пятеричная Десятичная Двенадцатеричная Двадцатеричная Славянская Древнеармянская Древнегрузинская Древнегреческая (ионийская) Прочие Машинные Римская Вавилонская Древнеегипетская Индийская Двоичная Восьмеричная Шестнадцатеричная   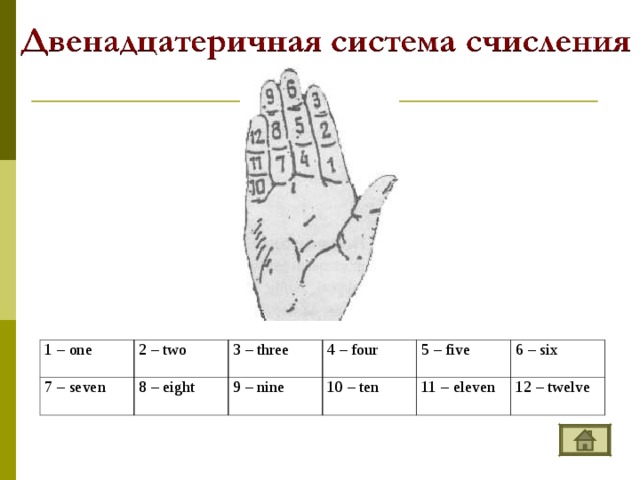 1 – one 7 – seven 2 – two 3 – three 8 – eight 4 – four 9 – nine 5 – five 10 – ten 11 – eleven 6 – six 12 – twelve 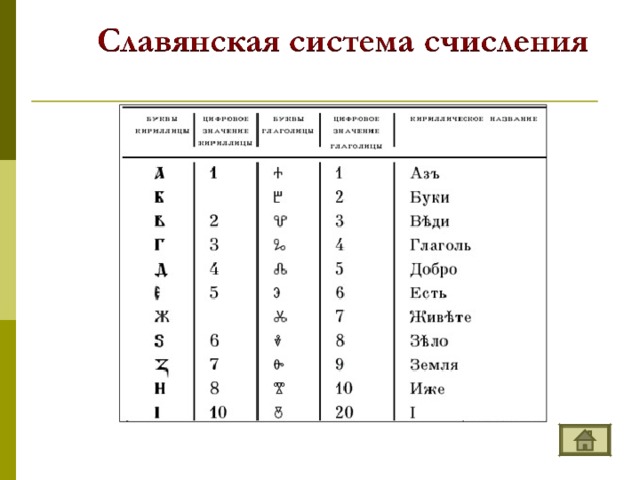   1 - I 2 - II 3 - III 4 - IIII 5 - Г 6 - ГI 7 - ГII 8 - ГIII 9 – ГIIII – 256 – 382 – 2051 – 7800 10 – 100 - H 1000 - X 10000 - M 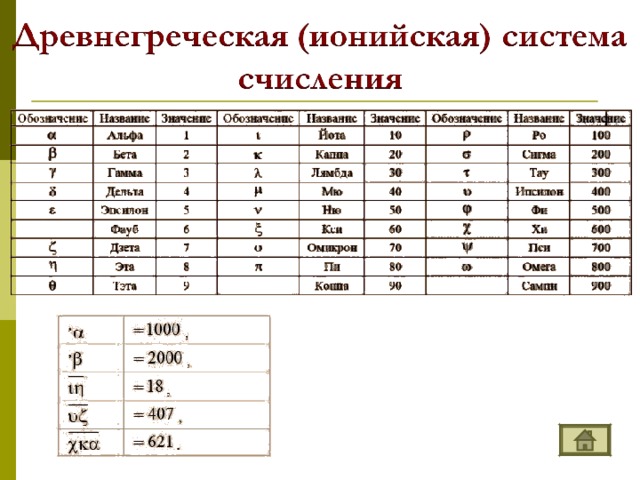  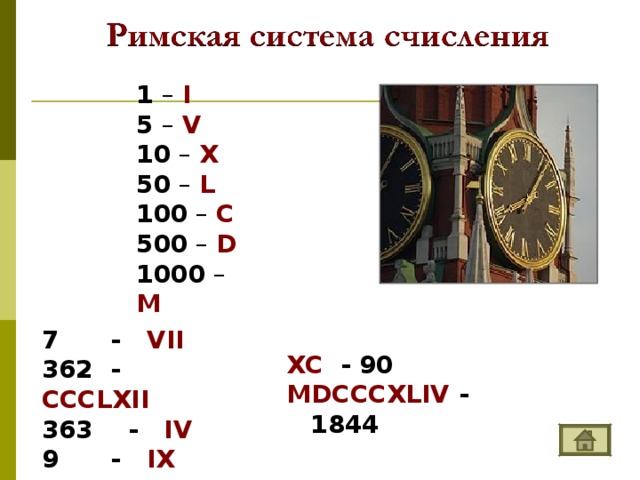 1 – I 5 – V 10 – X 50 – L 100 – C 500 – D 1000 – M 7 - VII - CCCLXII - IV 9 - IX XC - 90 MDCCCXLIV - 1844  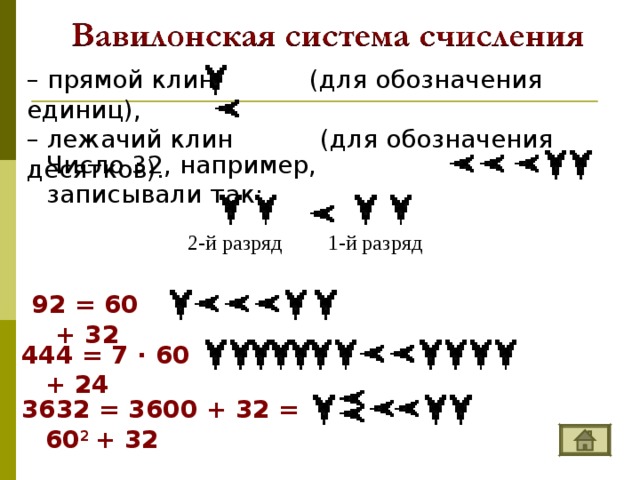 – прямой клин (для обозначения единиц), – лежачий клин (для обозначения десятков). Число 32, например, записывали так: 2-й разряд 1 -й разряд 92 = 60 + 32 444 = 7 · 60 + 24 3632 = 3600 + 32 = 60 2 + 32  Древнеегипетская система счисления  - единицы - десятки - сотни - тысячи 345 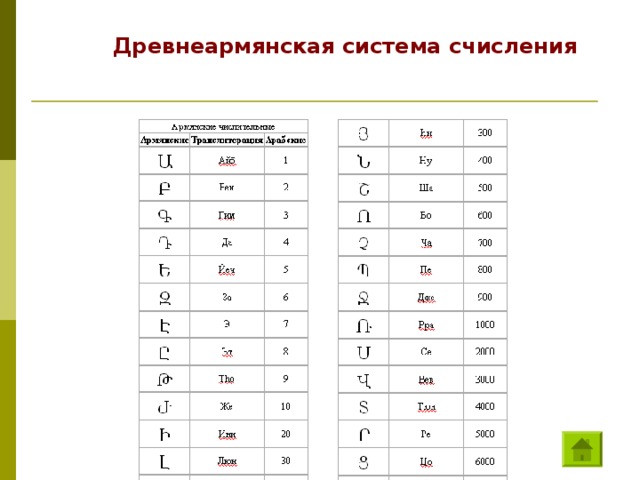 Древнеармянская система счисления  Индийская система счисления 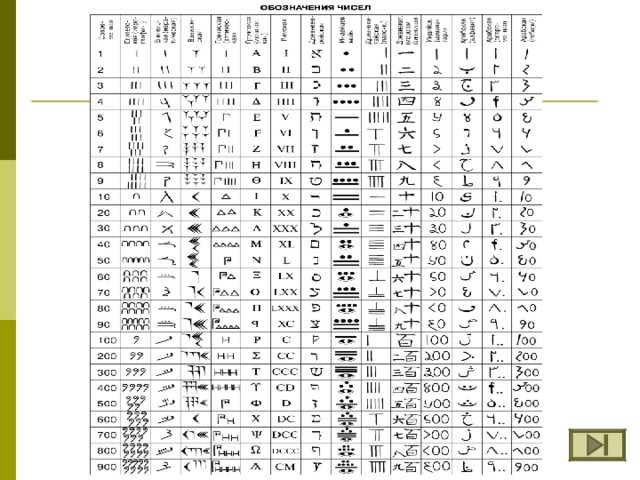 Системы счисления для общения с компьютером Двоичная система счисления Десятичная система счисления 0 1 Восьмеричная система счисления Десятичная система счисления, привычная для нас, не является наилучшей для использования в ЭВМ. Для изображения любого числа в десятичной системе счисления требуется десять различных символов. При реализации в ЭВМ этой системы счисления необходимы функциональные элементы, имеющие ровно десять устойчивых состояний, каждое из которых ставится в соответствие определенной цифре. Компьютеры используют двоичную систему потому, что она имеет ряд преимуществ перед другими системами: для ее реализации нужны технические устройства с двумя устойчивыми состояниями (есть ток — нет тока, намагничен — не намагничен и т.п.), а не, например, с десятью, — как в десятичной; представление информации посредством только двух состояний надежно и помехоустойчиво; возможно применение аппарата булевой алгебры для выполнения логических преобразований информации; двоичная арифметика намного проще десятичной. Недостаток двоичной системы — быстрый рост числа разрядов, необходимых для записи чисел. Широкое применение в ЭВМ нашли также восьмеричная и шестнадцатеричная системы счисления. Обмен информацией между устройствами большинства ЭВМ осуществляется путем передачи двоичных слов. Пользоваться такими словами из-за их большой длины и зрительной однородности человеку неудобно. Поэтому специалисты (программисты, инженеры) как на этапах составления несложных программ для микроЭВМ, их отладки, ручного ввода-вывода данных, так и на этапах их разработки, создания, настройки вычислительных систем заменяют коды машинных команд, адреса и операнды на эквивалентные им величины в восьмеричной или шестнадцатеричной системе счисления. В результате длина исходного слова сокращается в 3 или 4 раза соответственно. Это делает информацию более удобной для рассмотрения и анализа. Таким образом, восьмеричная и шестнадцатеричная системы счисления выступают в качестве простейшего языка общения человека с ЭВМ, достаточно близкого как к привычной для человека десятичной системе счисления, так и к двоичному "языку" машины. 0, 1, 2, 3, 4, 5, 6, 7 Шестнадцатеричная система счисления 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F 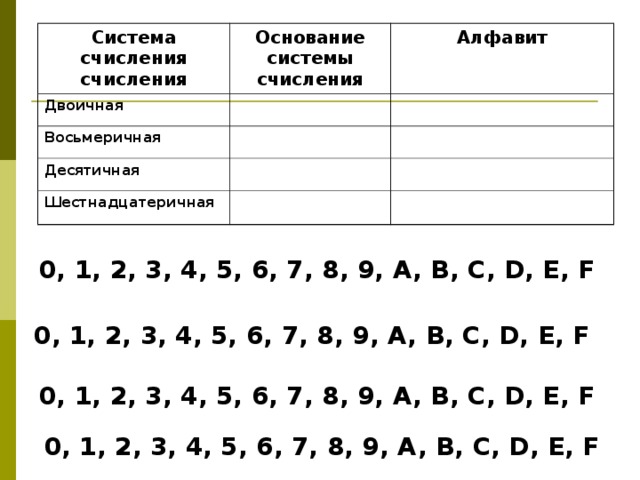 Система счисления счисления Основание системы счисления Двоичная Восьмеричная Алфавит Десятичная Шестнадцатеричная 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A , B, C, D, E, F 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A , B, C, D, E, F 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A , B, C, D, E, F 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A , B, C, D, E, F |
