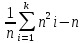Д. Ф. Устинова Кафедра
 Скачать 137.33 Kb. Скачать 137.33 Kb.
|
|
Министерство науки и высшего образования Балтийский государственный технический университет «ВОЕНМЕХ» им. Д.Ф. Устинова Кафедра  ДисциплинааМатематика Индивидуальное Домашнее задание № __19.1__ __________________________________________________________ __________________________________________________________ _________________________________________________________
Санкт-Петербург 2023 г. Содержание Введение 3 Вариационный ряд 4 Размах варьирования 5 Полигон частот и Эмпирическая функция распределения 6 Выборочное среднее и выборочная дисперсия 8 Сравнение эмпирических и теоретических частот 10 Доверительные Интервалы 12 Выводы 13 Список использованных источников: 14 ВведениеВ результате эксперимента получены данные, записанные в виде статистического ряда. Требуется: а) записать значения результатов эксперимента в виде вариационного ряда; б) найти размах варьирования и разбить его на 7 интервалов; в) построить полигон частот, гистограмму относительных частот и график эмпирической функции распределения; г) Найти числовые характеристики выборки д) принять в качестве нулевой гипотезу Н0: генеральная совокупность, из которой извлечена выборка, имеет нормальное распределение, проверить её, пользуясь критерием Пирсона при уровне значимости α=0,025; е) найти доверительные интервалы для математического ожидания и среднего квадратичного отклонения при степени надёжности γ=0,9 Вариационный ряда) записать значения результатов эксперимента в виде вариационного ряда; Таблица 1 - Вариационный ряд.
Размах варьированияб) Находим размах варьирования [1]. По формуле [2], где l - число интервалов, вычисляем длину частичного интервала:
В качестве границы первого интервала возьмём X(min). Границы следующих интервалов вычисляем по формуле: [3] и [4], где d=1,2,3…9. Находим середины интервалов: Подсчитываем число значений результатов эксперимента, попавших в каждый интервал, т.е. находим частоты интервалов n(i) . Далее вычисляем относительные частоты [5], (n=100) и их плотности [6] Все полученные результаты помещаем в таблицу 2. Таблица 2- Вычисление границ и относительных частот и её плотности.
Полигон частот и Эмпирическая функция распределенияв) построить полигон частот, гистограмму относительных частот и график эмпирической функции распределения; Рис. 1. Гистограмма относительных частот. 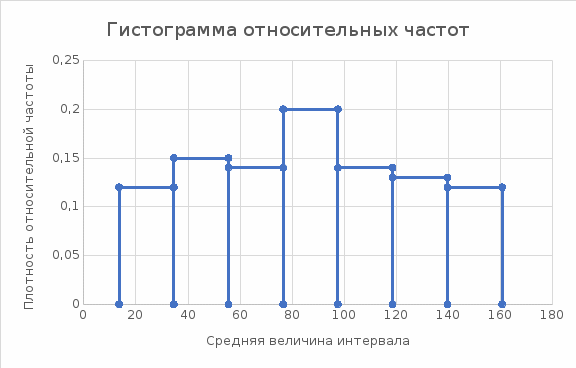 Таблица 3 – Значения эмпирической функции.
Рис. 2. Полигон частот. 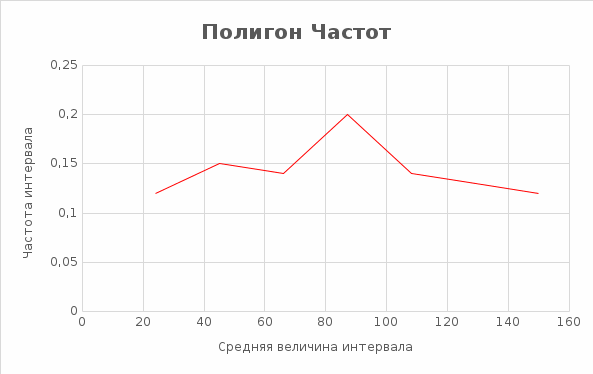 Рис. 3. График эмпирической функции. 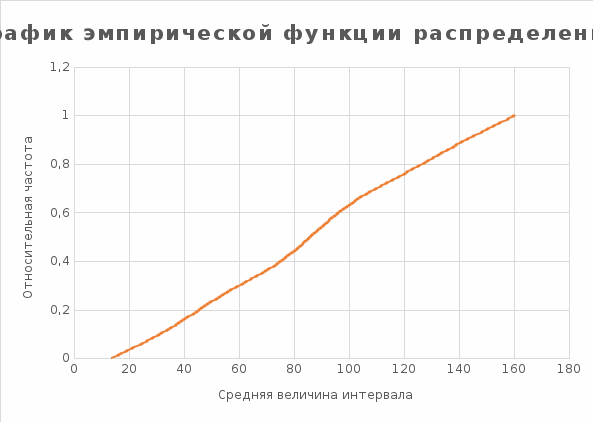 Выборочное среднее и выборочная дисперсия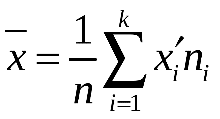 [7] [7]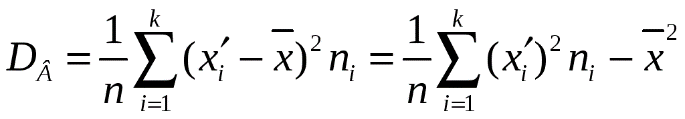 [8] [8]г) Найдём выборочное среднее [7] и выборочную дисперсию [8]. Составляем расчётную таблицу: Таблица 4 - Расчётная таблица №4, вычисление границ интервалов и её частот.
Таблица 5 – Нахождение выборочных средних значений и оценки.
Сравнение эмпирических и теоретических частотд). Согласно критерию Пирсона необходимо сравнить эмпирические и теоретические частоты. Эмпирические частоты даны. Найдём теоретические частоты. Для этого пронумеруем Х, т.е. перейдём к случайной величине [9] и вычислим концы интервалов: [10], причём наименьшее значение z, точнее z1 положим стремящимся к -бесконечности, а наибольшее, точнее Z(m+1) - стремящемся к + бесконечности. Вычислим всё в расчётных таблицах 6-8. Таблица 6 – Расчетная таблица №6.
Таблица 7 – Расчетная таблица №7.
Таблица 8 – Расчетная таблица № 8.
Доверительные Интервалые) найти доверительные интервалы для математического ожидания и среднего квадратичного отклонения при степени надёжности γ=0,9. Таблица 9 – Расчётная таблица № 9.
Доверительный интервал :(Хср - (σв2/√n) *ty; Хср + (σв2/√n)*ty) (78,2610; 94,0589) Доверительный интервал, покрывающий среднее квадратичное отклонение σ, где q = 0,143: (σв2(1-q);σв2(1+q)) (34,12; 45,506) 34,12 ВыводыВ данном задании из предложенных чисел, разбросанных хаотично, мы составили вариационный ряд, что позволило нам отсортировать значения и в дальнейшем проанализировать. Следующим этапом мы разбили значения на интервалы, чтобы найти интервалы варьирования. С помощью полученных результатов мы построили Гистограмму, полигон частот, график эмпирической функции распределения, с помощью которых мы можем наглядно видеть, как часто попадаются те или иные значения. Также был вычислен доверительный интервал, который характеризует усредненные значения величин. Список использованных источников:Математическая статистика: Учеб. Для студ. сред. спец. учеб. образования/В. Н. Калинина, В. Ф. Панкин. 4-е изд.,испр. М.: Дрофа, 2002. — 336 с. СБОРНИК ИДЗ РЯБУШКО А.П. 4 ЧАСТЬ. [Электронный ресурс]. – URL: https://studfile.net/preview/5836550/ . Дата обращения 12.02.2023 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

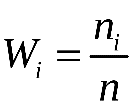 [5]
[5]
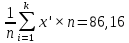
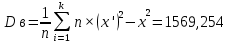
 в = 39,61382
в = 39,61382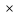 Dв = 1585,105
Dв = 1585,105