Министерство науки и высшего образования
Балтийский государственный технический университет
«ВОЕНМЕХ» им. Д.Ф. Устинова
Кафедра

ДисциплинааМатематика
Индивидуальное Домашнее задание № __19.1__
__________________________________________________________
__________________________________________________________
_________________________________________________________
Выполнили студенты
|
Чудов.С
Львов.И
|
Фамилия И.О.
|
группа
|
А411С
_________________
|
|
|
Преподаватель
|
Еськова.Е.А
|
|
Фамилия И. О.
|
|
Подпись преподавателя
|
Дата
|
Допуск
|
|
|
Выполнение
|
|
|
|
|
|
Санкт-Петербург
2023 г.
В результате эксперимента получены данные, записанные в виде статистического ряда.
Требуется:
а) записать значения результатов эксперимента в виде вариационного ряда;
б) найти размах варьирования и разбить его на 9 интервалов;
в) построить полигон частот, гистограмму относительных частот и график эмпирической функции распределения;
г) Найти числовые характеристики выборки 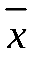 и и 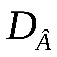 ; ;
д) принять в качестве нулевой гипотезу Н0: генеральная совокупность, из которой извлечена выборка, имеет нормальное распределение, проверить её, пользуясь критерием Пирсона при уровне значимости 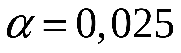 ; ;
е) найти доверительные интервалы для математического ожидания и среднего квадратичного отклонения при степени надёжности 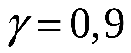
а) записать значения результатов эксперимента в виде вариационного ряда;
Таблица 1.
15
|
16
|
17
|
17
|
18
|
19
|
21
|
25
|
30
|
32
|
33
|
34
|
35
|
36
|
37
|
38
|
39
|
40
|
41
|
48
|
49
|
50
|
51
|
52
|
53
|
54
|
55
|
56
|
57
|
61
|
64
|
65
|
66
|
67
|
68
|
69
|
70
|
71
|
72
|
73
|
76
|
77
|
78
|
80
|
81
|
82
|
84
|
85
|
86
|
87
|
88
|
89
|
90
|
91
|
92
|
93
|
93
|
94
|
94
|
96
|
97
|
98
|
99
|
100
|
101
|
102
|
103
|
104
|
105
|
109
|
110
|
112
|
113
|
114
|
115
|
121
|
123
|
124
|
125
|
126
|
128
|
129
|
130
|
131
|
135
|
137
|
138
|
139
|
140
|
141
|
142
|
144
|
145
|
146
|
147
|
149
|
150
|
151
|
158
|
159
|
б) Находим размах варьирования 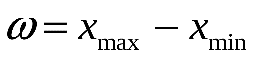 . По формуле . По формуле 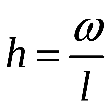 , где , где 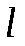 - число интервалов, вычисляем длину частичного интервала: - число интервалов, вычисляем длину частичного интервала:
В качестве границы первого интервала возьмём X(min). Границы следующих интервалов вычисляем по формуле: 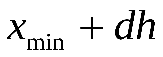 , где , где 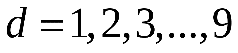 . .
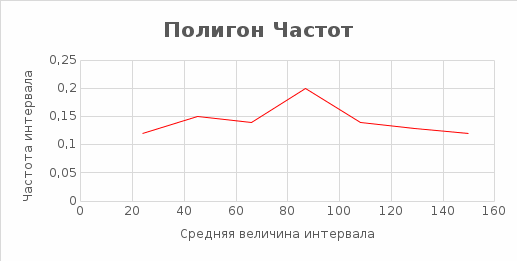
Находим середины интервалов: 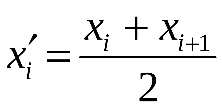 . Подсчитываем число значений результатов эксперимента, попавших в каждый интервал, т.е. находим частоты интервалов . Подсчитываем число значений результатов эксперимента, попавших в каждый интервал, т.е. находим частоты интервалов 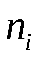 . Далее вычисляем относительные частоты . Далее вычисляем относительные частоты 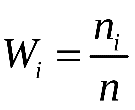 , ( , (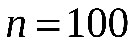 ) и их плотности ) и их плотности 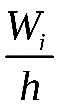
Таблица 2.
Номер частичного интервала
|
Границы интервала
|
Середина интервала
|
Частота интервала
|
Относительная частота
|
Плотность относительной частоты
|
1
|
13,5
|
34,5
|
24
|
12
|
0,12
|
0,0057
|
2
|
34,5
|
55,5
|
45
|
15
|
0,15
|
0,0071
|
3
|
55,5
|
76,5
|
66
|
14
|
0,14
|
0,0067
|
4
|
76,5
|
97,5
|
87
|
20
|
0,2
|
0,0095
|
5
|
97,5
|
118,5
|
108
|
14
|
0,14
|
0,0067
|
6
|
118,5
|
139,5
|
129
|
13
|
0,13
|
0,0062
|
7
|
139,5
|
160,5
|
150
|
12
|
0,12
|
0,0057
|
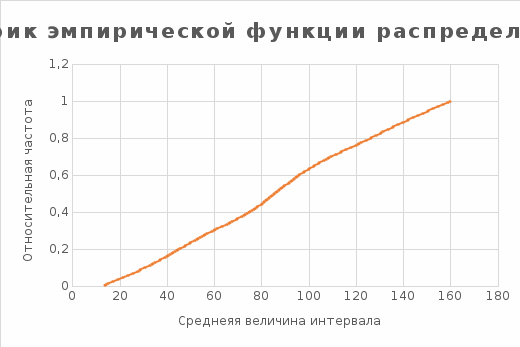
в) построить полигон частот, гистограмму относительных частот и график эмпирической функции распределения;

Таблица 3.
F(13,5)
|
0
|
F(34,5)
|
0,12
|
F(55,5)
|
0,27
|
F(76,5)
|
0,41
|
F(97,5)
|
0,61
|
F(118,5)
|
0,75
|
F(139,5)
|
0,88
|
F(160,5)
|
1
|
г) Найдём выборочное среднее 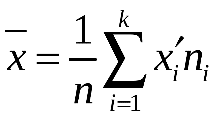 и выборочную дисперсию и выборочную дисперсию 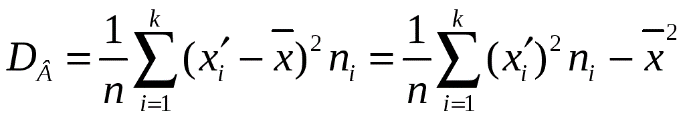
Составляем расчётную таблицу:
Таблица 4.
m
|
Граница интервала x
|
Частота интервала, n
|
n*x'
|
(x')^2
|
n*(x')^2
|
Середина интервала,x'
|
1
|
13,5
|
34,5
|
12
|
288
|
576
|
6912
|
24
|
2
|
34,5
|
55,5
|
15
|
675
|
2025
|
30375
|
45
|
3
|
55,5
|
76,5
|
14
|
924
|
4356
|
60984
|
66
|
4
|
76,5
|
97,5
|
20
|
1740
|
7569
|
151380
|
87
|
5
|
97,5
|
118,5
|
14
|
1512
|
11664
|
163296
|
108
|
6
|
118,5
|
139,5
|
13
|
1677
|
16641
|
216333
|
129
|
7
|
139,5
|
160,5
|
12
|
1800
|
22500
|
270000
|
150
|
∑
|
|
|
100
|
8616
|
|

xср = 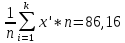
899280
|
|
Таблица 5.
Выборочное среднее xср
|
|
|
|
|
|
|
|
|
Выборочная дисперсия Dв
|
|
|
|
|
|
|
|
|

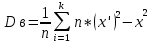 =1569,254 =1569,254
|
Выб. ср. квадр. Откл. σв
|

σв =  в=39,61382 в=39,61382
|
|
|
|
|
|
|
|
|
Несмещенная оценка σв2
|
σв2 = √Dв2=39,81338
|
|
|
|
|
|
|
|

Dв2 =(n/(n-1)) * Dв=1585,105
|
Смещенная оценка Dв2
|
|
д) Согласно критерию Пирсона необходимо сравнить эмпирические и теоретические частоты. Эмпирические частоты даны. Найдём теоретические частоты. Для этого пронумеруем Х, т.е. перейдём к случайной величине 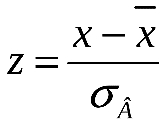 и вычислим концы интервалов: и вычислим концы интервалов: 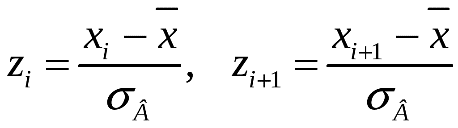 , причём наименьшее значение , причём наименьшее значение  , точнее , точнее 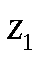 положим стремящимся к положим стремящимся к 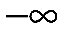 , а наибольшее, точнее , а наибольшее, точнее 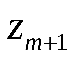 - стремящемся к - стремящемся к 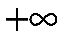 . .
Таблица 6.
i
|
Границы интервала Xi; Xi+1
|
Xi-Xср
|
Xi+1-Xср
|
Границы интервала Zi; Zi+1
|
|
Xi
|
Xi+1
|
|
|
|
Zi = (Xi-Xср) / σв
|
Zi+1 = (Xi+1-Xср) / σв
|
|
1
|
13,5
|
34,5
|
|
-72,66
|
-51,66
|
-
|
-1,30409
|
|
2
|
34,5
|
55,5
|
|
-51,66
|
-30,66
|
-1,30409
|
-0,77397
|
|
3
|
55,5
|
76,5
|
|
-30,66
|
-9,66
|
-0,77397
|
-0,24385
|
|
4
|
76,5
|
97,5
|
|
-9,66
|
11,34
|
-0,24385
|
0,286264
|
|
5
|
97,5
|
118,5
|
|
11,34
|
32,34
|
0,286264
|
0,816382
|
|
6
|
118,5
|
139,5
|
|
32,34
|
53,34
|
0,816382
|
1,3465
|
|
7
|
139,5
|
160,5
|
|
53,34
|
74,34
|
1,3465
|
-
|
|
Таблица 7.
i
|
Границы интервала Xi; Xi+1
|
Ф(Zi )
|
Ф(Zi+1 )
|
Pi = Ф(Zi+1 ) - Ф(Zi )
|
n'I = 100Pi
|
|
Zi
|
Zi+1
|
|
|
|
|
|
1
|
-
|
-1,30409
|
|
-0,5
|
-0,4039
|
0,096101
|
|
9,610137
|
2
|
-1,30409
|
-0,77397
|
|
-0,4039
|
-0,28053
|
0,123372
|
|
12,33722
|
3
|
-0,77397
|
-0,24385
|
|
-0,28053
|
-0,09633
|
0,184198
|
|
18,41983
|
4
|
-0,24385
|
0,286264
|
|
-0,09633
|
0,112662
|
0,20899
|
|
20,89901
|
5
|
0,286264
|
0,816382
|
|
0,112662
|
0,292859
|
0,180197
|
|
18,01972
|
6
|
0,816382
|
1,3465
|
|
0,292859
|
0,410929
|
0,11807
|
|
11,80702
|
7
|
1,3465
|
-
|
|
0,410929
|
0,5
|
0,089071
|
|
8,907067
|
Сумма
|
|
|
|
|
|
1
|
|
100
|
Таблица 8.
i
|
ni
|
n'i
|
ni-n'i
|
(ni-n'i)^2
|
(ni-n'i)^2/n'i
|
ni^2
|
ni^2/n'i
|
1
|
12
|
9,610137
|
2,389863
|
5,711446
|
0,594315
|
144
|
14,98418
|
2
|
15
|
12,33722
|
2,662781
|
7,090403
|
0,574716
|
225
|
18,2375
|
3
|
14
|
18,41983
|
-4,41983
|
19,53487
|
1,060535
|
196
|
10,64071
|
4
|
20
|
20,89901
|
-0,89901
|
0,808223
|
0,038673
|
400
|
19,13966
|
5
|
14
|
18,01972
|
-4,01972
|
16,15812
|
0,896691
|
196
|
10,87697
|
6
|
13
|
11,80702
|
1,192978
|
1,423197
|
0,120538
|
169
|
14,31352
|
7
|
12
|
8,907067
|
3,092933
|
9,566233
|
1,074005
|
144
|
16,16694
|
∑
|
100
|
100
|
-
|
-
|
4,359
|
-
|
104,3595
|

X^2набл = 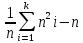
|
4,359
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Контроль: ∑n^2i/n'I - n
|
4,359
|
|
|
|
|
|
|
|
|
|
|
Число степени свободы k:
|
4
|
|
|
|
|
|
|
|
|
|
|
X^2кр =
|
13,3
|
|
|
|
|
|
|
|
|
|
|
Так как X^2набл < X^2кр, то гипотеза H0 о нормальном распределении генеральной совокупности принимается
|
|
|
|
|
|
Таблица 9.
Доверительный интервал :(Хср - (σв2/√n)*ty; Хср + (σв2/√n)*ty)
(78,2610; 94,0589)
Доверительный интервал, покрывающий среднее квадратичное отклонение σ, где q = 0,143: (σв2(1-q);σв2(1+q))
(34,12; 45,506)
34,12 |
 Скачать 145.9 Kb.
Скачать 145.9 Kb.



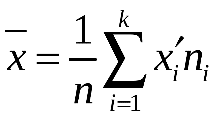 и выборочную дисперсию
и выборочную дисперсию 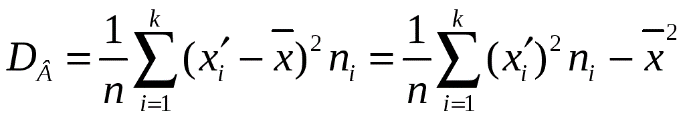
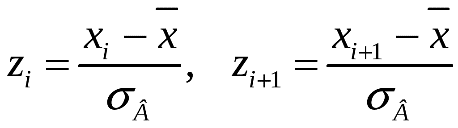 , причём наименьшее значение
, причём наименьшее значение 

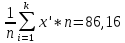

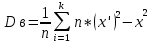 =1569,254
=1569,254
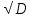 в=39,61382
в=39,61382