Алгоритмы обхода связного графа.
Перечислить вершины графа в порядке обхода а) в глубину; в) в ширину.
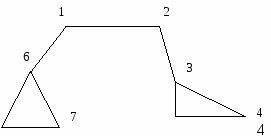
8
Граф задан матрицей смежности. Найти
Какой-либо путь из вершины 2 в вершину 4;
кратчайший путь из вершины 2 в вершину 4;
кратчайшие пути из вершины 2 ко всем остальным вершинам.
-
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
1
|
0
|
1
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
2
|
1
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
3
|
0
|
1
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
4
|
0
|
0
|
1
|
0
|
1
|
1
|
0
|
1
|
1
|
0
|
5
|
1
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
6
|
0
|
0
|
0
|
1
|
0
|
0
|
1
|
0
|
0
|
0
|
7
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
1
|
0
|
1
|
8
|
0
|
0
|
0
|
1
|
0
|
0
|
1
|
0
|
0
|
0
|
9
|
0
|
1
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
10
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
На клетчатом листе бумаги размером 10 х 10 закрашены некоторые клетки. Разрешается ходить по не закрашенным клеткам, переходя на каждом шаге вверх, вниз, вправо или влево. Описать алгоритм, отвечающий на следующие вопросы:
А. Есть ли путь из левой нижней клетки в правую верхнюю;
Б. Какое минимальное число шагов нужно сделать, чтобы пройти этот путь;
В. По каким клеткам при этом надо идти
В двузначном числе за один ход разрешается заменить любую цифру суммой цифр по модулю 10. Заданы два двузначных числа a и b. Написать программу, которая определяет: можно ли построить цепочку ходов, которая переводит a в b; минимальную такую цепочку. В двузначном числе старшая цифра может быть и нулем.
На шахматной доске N х N, несколько клеток, которой вырезано, заданы две клетки. Построить минимальный путь коня из одной данной клетки в другую.
В таблице N x N, где N<13, клетки заполнены случайным образом цифрами от 0 до 9. Предложить алгоритм, позволяющий найти маршрут из клетки (1,1) в клетку (N,N) и удовлетворяющий следующим условиям:
любые две последовательные клетки в маршруте имеют общую сторону;
количество клеток маршрута минимально;
из всех маршрутов, удовлетворяющих условиям 1) и 2), искомый маршрут тот, сумма цифр в клетках которого максимальна.
|
 Скачать 2.66 Mb.
Скачать 2.66 Mb.
