Деревья
Докажите, что граф, в котором любые две вершины соединены ровно одной цепью, является деревом.
Докажите, что в дереве любые две вершины соединены ровно одной цепью.
Докажите, что в дереве с р вершинами р–1 ребро.
Докажите, что связный граф, у которого число ребер на единицу меньше числа вершин, является деревом.
Докажите, что в дереве есть вершина, из которой выходит ровно одно ребро (такая вершина называется висячей).
Докажите, что в любом нетривиальном дереве имеются, по крайней мере, две висячие вершины.
Докажите, что при удалении любого ребра из дерева оно превращается в несвязный граф.
Какое максимальное число висячих вершин может иметь дерево, обладающее 9 вершинами?
В графе все вершины имеют степень 3. Докажите, что в нем есть цикл.
В парке «Лотос» невозможно найти такой маршрут для прогулок по его дорожкам, который начинается и оканчивается в одной и той же точке и каждую дорожку содержит не более одного раза. Докажите, что некоторые дорожки парка приводят в тупик.
В стране 101 город, и некоторые из них соединены дорогами. При этом любые два города соединяет ровно один путь. Сколько в этой стране дорог?
Докажите, что в любом связном графе можно удалить вершину вместе со всеми выходящими из нее ребрами так, чтобы он остался связным.
Сколько ребер нужно удалить из связного графа, имеющего q ребер и p вершин, чтобы получить дерево, содержащее все вершины этого графа.
Докажите, что полный двудольный граф с n вершинами в одной доле и m вершинами в другой имеет не менее mn-m-n+1 различных циклов?
Найдите цикломатическое число для графов:
Кn;
Кm,n;
Wn;
графа Петерсона;
любого связного регулярного графа с n вершинами степени регулярности r.
В некоторой стране 30 городов, причем каждый соединен с каждым дорогой. Какое наибольшее число дорог можно закрыть на ремонт так, чтобы из каждого города можно было проехать в каждый?
В несвязном графе с 5 компонентами связности любое ребро является мостом. Сколько вершин в графе, если ребер 115?
П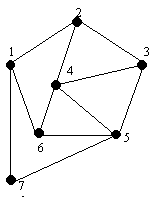
остройте остовы графа, изображенного на рисунке методами поиска в ширину и в глубину.
Найти минимальный каркас графа, изображенного на рисунке, используя алгоритм Краскала.
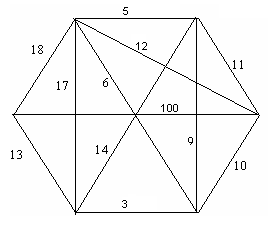
Найдите какие-нибудь остовные деревья для графов К5, К33, и в графе Петерсона.
Постройте каркас минимального веса для графа заданного матрицей весов
0
|
|
|
|
|
3
|
2
|
|
0
|
10
|
|
|
4
|
|
|
10
|
0
|
|
|
4
|
|
|
|
|
0
|
2
|
3
|
|
|
|
|
2
|
0
|
1
|
|
3
|
4
|
4
|
3
|
1
|
0
|
1
|
2
|
|
|
|
|
1
|
0
|
0
|
20
|
|
|
|
15
|
|
20
|
0
|
|
|
1
|
|
3
|
|
|
0
|
5
|
2
|
|
2
|
|
|
5
|
0
|
3
|
|
1
|
|
1
|
2
|
3
|
0
|
10
|
|
15
|
|
|
|
10
|
0
|
|
|
3
|
2
|
1
|
|
|
0
|
0
|
2
|
|
|
|
7
|
10
|
2
|
0
|
10
|
|
|
1
|
0
|
|
10
|
0
|
2
|
|
|
|
|
|
2
|
0
|
5
|
1
|
|
|
|
|
5
|
0
|
3
|
|
7
|
1
|
|
1
|
3
|
0
|
2
|
10
|
|
|
|
|
2
|
0
| Найти каркас минимального веса для полного графа на множестве вершин (х1, х2, х3, х4), как показано на рисунке, с весами ребер, определенных как расстояния между вершинами.
Д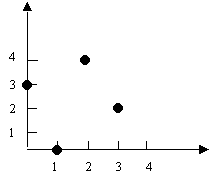
ля графа G, заданного матрицей весов, построить минимальный по весу остов и найти его вес:
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
1
|
-
|
10
|
∞
|
5
|
∞
|
∞
|
14
|
2
|
10
|
-
|
6
|
2
|
4
|
8
|
∞
|
3
|
∞
|
6
|
-
|
3
|
1
|
1
|
∞
|
4
|
5
|
2
|
3
|
-
|
6
|
∞
|
3
|
5
|
∞
|
4
|
1
|
6
|
-
|
5
|
∞
|
6
|
∞
|
8
|
1
|
∞
|
5
|
-
|
2
|
7
|
14
|
∞
|
∞
|
3
|
∞
|
2
|
-
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
1
|
-
|
7
|
15
|
12
|
∞
|
10
|
∞
|
2
|
7
|
-
|
13
|
9
|
∞
|
∞
|
8
|
3
|
15
|
13
|
-
|
7
|
15
|
7
|
∞
|
4
|
12
|
9
|
7
|
-
|
9
|
∞
|
11
|
5
|
∞
|
∞
|
15
|
9
|
-
|
10
|
∞
|
6
|
10
|
∞
|
7
|
∞
|
10
|
-
|
12
|
7
|
∞
|
8
|
∞
|
11
|
∞
|
12
|
-
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
1
|
-
|
10
|
11
|
∞
|
14
|
∞
|
12
|
2
|
10
|
-
|
10
|
9
|
∞
|
∞
|
7
|
3
|
11
|
10
|
-
|
12
|
10
|
∞
|
6
|
4
|
∞
|
9
|
12
|
-
|
9
|
12
|
∞
|
5
|
14
|
∞
|
10
|
9
|
-
|
11
|
12
|
6
|
∞
|
∞
|
∞
|
12
|
11
|
-
|
∞
|
7
|
12
|
7
|
6
|
∞
|
12
|
∞
|
-
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
1
|
-
|
3
|
5
|
∞
|
6
|
∞
|
∞
|
2
|
3
|
-
|
10
|
6
|
8
|
∞
|
4
|
3
|
5
|
10
|
-
|
5
|
7
|
∞
|
9
|
4
|
∞
|
6
|
5
|
-
|
8
|
7
|
∞
|
5
|
6
|
8
|
7
|
8
|
-
|
9
|
11
|
6
|
∞
|
∞
|
∞
|
7
|
9
|
-
|
∞
|
7
|
∞
|
4
|
9
|
∞
|
11
|
∞
|
-
|
На строительном участке нужно создать телефонную сеть, соединяющую все бытовки. Для того чтобы телефонные линии не мешали строительству, их решили проводить вдоль дорог. Схема участка изображена на рисунке, где бытовкам соответствуют вершины графа и указаны длины дорог между ними. Каким образом провести телефонные провода, чтобы их общая длина была минимальной?
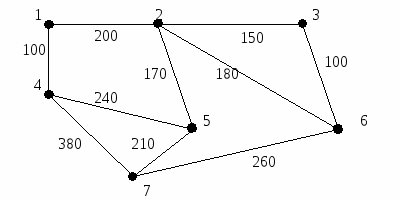
Необходимо построить систему нефтепроводов, которые должны соединять семь нефтеочистительных заводов (Н1, Н2, Н3, Н4, Н5, Н6, Н7) , принадлежащих некоторой компании, с портом (П), куда поступает импортируемая сырая нефть. Стоимость прокладки нефтепровода между любыми двумя пунктами составляет 5000 долларов в расчете на одну милю. расстояния между всеми парами вершин задаются в следующей таблице:
-
|
П
|
Н1
|
Н2
|
Н3
|
Н4
|
Н5
|
Н6
|
Н7
|
П
|
0
|
5
|
6
|
8
|
2
|
6
|
9
|
10
|
Н1
|
|
0
|
4
|
10
|
5
|
8
|
6
|
10
|
Н2
|
|
|
0
|
11
|
8
|
4
|
9
|
10
|
Н3
|
|
|
|
0
|
10
|
3
|
6
|
7
|
Н4
|
|
|
|
|
0
|
2
|
5
|
9
|
Н5
|
|
|
|
|
|
0
|
10
|
5
|
Н6
|
|
|
|
|
|
|
0
|
8
|
Н7
|
|
|
|
|
|
|
|
0
| Найдите минимальную стоимость прокладки нефтепровода.
Есть бактерия, которая делится на 3 бактерии. В дальнейшем появляющиеся бактерии могут делиться на 4 бактерии, могут делиться на две, а могут и не делиться. Образовалось 102 бактерии. Определите число делений, если известно, что число бактерий, разделившихся на две в 6 раз больше, чем число бактерий, разделившихся на четыре.
Насыщенным углеводородом называется соединение углерода С, имеющего валентность 4, и водорода Р, имеющего валентность 1, в котором при заданном числе атомов углерода содержится наибольшее число атомов водорода. Напишите формулу насыщенного углеводорода, содержащего n атомов углерода.
Город имеет форму квадрата (100n x 100n) метров с (n+1) прямолинейной улицей, идущей параллельно одной стороне квадрата, и (n+1) прямолинейной улицей, идущей параллельно другой его стороне. Расстояние между любыми двумя соседними параллельными улицами – 100 метров, длина каждой улицы – 100n метров. Мэр города решил выполнить свое предвыборное обещание: заасфальтировать за свой счет улицы так, чтобы с любого перекрестка на любой другой можно было проехать по асфальту. Конечно, мэр хочет истратить как можно меньше своих денег. Какой наименьшей длины асфальтовое покрытие улиц может сделать мэр?
|
 Скачать 2.66 Mb.
Скачать 2.66 Mb.
