АВЛ дерево. Отчет ЛР №1. Отчет по лабораторной работе 1 по дисциплине Структуры и алгоритмы обработки данных на эвм
 Скачать 91.5 Kb. Скачать 91.5 Kb.
|
|
Министерство науки и высшего образования Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР) Кафедра автоматизированных систем управления (АСУ) БИНАРНЫЕ ДЕРЕВЬЯ Вариант 11 Отчет по лабораторной работе № 1 по дисциплине «Структуры и алгоритмы обработки данных на ЭВМ» Выполнил: _______________ Студент гр. з-430П5-1 Волчок Ирина Викторовна «07» ноября 2021г. Проверил: ________________ _________________________ «____» _____________ 20__ г. Томск 2021г. Содержание 1. Тема работы 4 2. Цель работы 4 3. Индивидуальное задание 4 Вариант № 11 4 Дана последовательность чисел, написать программу, которая формирует АВЛ-дерево, выводит построенное дерево на экран и подсчитывает число вершин на n-ом уровне сформированного дерева. Корень считать вершиной 0-ого уровня. После выполнения программы очистить память, занятую древовидной структурой. 4 4. Алгоритм решения задачи 4 5. Результаты работы программы 5 6. Выводы 6 Приложение А. Листинг программы 7 1. Тема работы Лабораторная номер 1: бинарные деревья. 2. Цель работы Цель лабораторной работы № 1 — получить практические навыки представления в памяти ЭВМ структуры данных «бинарное дерево», реализовать на языке программирования C/C++ алгоритмы работы с деревьями. 3. Индивидуальное задание Вариант № 11 Дана последовательность чисел, написать программу, которая формирует АВЛ-дерево, выводит построенное дерево на экран и подсчитывает число вершин на n-ом уровне сформированного дерева. Корень считать вершиной 0-ого уровня. После выполнения программы очистить память, занятую древовидной структурой. 4. Алгоритм решения задачи 1. Пользователь вводит число maxnum 2. Программа генерирует случайные числа элементов дерева. 2. Добавляет каждый новый узел в дерево, сохраняя балансировку дерева по высоте, используя для этого соответствующие функции поворота. 3. Выводит построенное дерево на экран 4. Пользователь вводит уровень на котором нужно посчитать число вершин 5. Программа находит введенный уровень, подсчитывает количество вершин на уровне 6. Выводит список вершин на указанном уровне 7. Удаляет дерева из памяти. 5. Результаты работы программы Программа проверяет пустоту дерева и при вводе числа maxnum равное 0 либо отрицательному числу, программа выводит сообщение «Дерево пустое!» и завершает работу 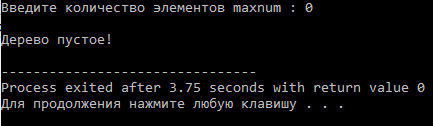 Если дерево не пустое, программа выводит на экран сгенерированный список и постоенное АВЛ дерево. 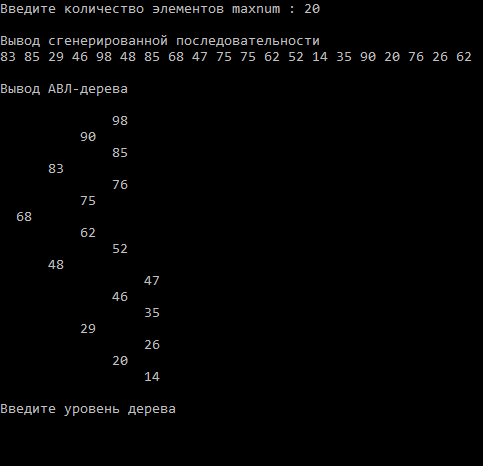 После ввода уровня, программа находит нужный уровень, подсчитывает общее количество вершин на уровне, выводит значение вершин 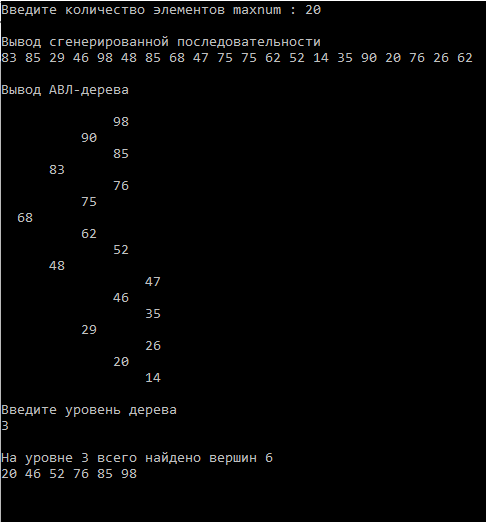 6. Выводы В лабораторной работе разработана программа выполняющая построение бинарного дерева на основе сгенерированных чисел. Программа выводит число вершин на n-ом уровне сформированного дерева. Уровень пользователь задает при помощи ввода с клавиатуры. Приложение А. Листинг программы #include #include #include #include #include #include typedef int ElementType; typedef struct AvlNode *Position; typedef struct AvlNode *AvlTree; struct AvlNode { ElementType Element; AvlTree Left; AvlTree Right; int Height; }; AvlTree MakeEmpty( AvlTree T ); Position Find( ElementType X, AvlTree T ); Position FindMin( AvlTree T ); Position FindMax( AvlTree T ); AvlTree Insert( ElementType X, AvlTree T ); ElementType Retrieve( Position P ); void printTree(AvlTree T, int l = 0); //функция удаления вершины и ее поддеревьев AvlTree MakeEmpty( AvlTree T ) { if( T != NULL ) { MakeEmpty( T->Left ); MakeEmpty( T->Right ); free( T ); } return NULL; } //функция возвращает вес вершины int Height( Position P ) { if( P == NULL ) return -1; else return P->Height; } //функция возвращает максимальное из двух чисел int Max( int Lhs, int Rhs ) { if(Lhs > Rhs) return Lhs; return Rhs; } /*функция выполняет правый поворот между вершиной K2 и ее левым потомком*/ Position SingleRotateWithLeft( Position K2 ) { Position K1; K1 = K2->Left;//записываем левый указатель на потомка дерева K2->Left = K1->Right; K1->Right = K2; K2->Height = Max(Height(K2->Left), Height(K2->Right)) + 1; K1->Height = Max( Height( K1->Left ), K2->Height ) + 1; return K1; //Новый корень } /*функция выполняет левый поворот между вершиной K1 и ее правым потомком*/ Position SingleRotateWithRight( Position K1 ) { Position K2; K2 = K1->Right;/*записываем правый указатель на потомка дерева*/ K1->Right = K2->Left; K2->Left = K1; K1->Height = Max(Height(K1->Left), Height(K1->Right)) + 1; K2->Height = Max( Height( K2->Right ), K1->Height ) + 1; return K2; //новый корень } //функция выполняет двойной лево-правый поворот Position DoubleRotateWithLeft( Position K3 ) { // поворот между K1 и K2/ K3->Left = SingleRotateWithRight( K3->Left ); // поворот между K3 и K2 return SingleRotateWithLeft( K3 ); } //функция выполняет двойной право-левый поворот Position DoubleRotateWithRight( Position K1 ) { // поворот между K3 и K2 K1->Right = SingleRotateWithLeft( K1->Right ); // поворот между K1 и K2 return SingleRotateWithRight( K1 ); } //функция вставки вершины в АВЛ-дерево AvlTree Insert( ElementType X, AvlTree T ){ if( T == NULL ) { T = (AvlTree) malloc(sizeof(AvlNode)); if( T == NULL ) printf("Недостаточно памяти!!!\n" ); else { T->Element = X; T->Height = 0; T->Left = T->Right = NULL; } } else if( X < T->Element ) { T->Left = Insert( X, T->Left ); if( Height( T->Left ) - Height( T->Right ) == 2 ) if( X < T->Left->Element ) T = SingleRotateWithLeft( T ); else T = DoubleRotateWithLeft( T ); } else if( X > T->Element ) { T->Right = Insert( X, T->Right ); if( Height( T->Right ) - Height( T->Left ) == 2 ) if( X > T->Right->Element ) T = SingleRotateWithRight( T ); else T = DoubleRotateWithRight( T ); } T->Height = Max(Height(T->Left), Height(T->Right)) + 1; return T; } //функция возвращает значение, хранящееся в вершине ElementType Retrieve( Position P ) { return P->Element; } //функция вывода АВЛ-дерева на печать void printTree(AvlTree T, int l){ int i; if ( T != NULL ) { printTree(T->Right, l+1); for (i=0; i < l; i++) printf(" "); printf ("%4ld", Retrieve ( T )); printTree(T->Left, l+1); } else printf("\n"); } //функция поиска вершин int topCount(AvlTree T, int Level) { if (T == NULL) return 0; if (Level < 0) return 0; if (Level == 0) return 1; //Уровень найден. return topCount(T->Left, Level - 1) + topCount(T->Right, Level - 1); //Сумма количества в левом и правом поддеревьях } //Вывести список элементов нужного уровня void WriteAt(AvlTree T, int Level) { if (T == NULL) return; if (Level < 0) return; if (Level == 0) //Это вершина нужного уровня { printf("%d ", Retrieve ( T )); return; } WriteAt(T->Left, Level - 1); WriteAt(T->Right, Level - 1); } int main() { SetConsoleCP(1251); SetConsoleOutputCP(1251); int i, *a, maxnum; AvlTree T; Position P; int j = 0; printf("Введите количество элементов maxnum : "); scanf("%d",&maxnum); printf("\n"); a = (int*) malloc(sizeof(int)*maxnum); srand(time(NULL)*1000); //Проверка пустоты дерева if (maxnum <= 0) { printf("Дерево пустое!\n"); exit(0);} else // генерация массива for (i = 0; i < maxnum; i++) a[i] = rand()%100; printf("Вывод сгенерированной последовательности\n"); for (i = 0; i < maxnum; i++) printf("%d ",a[i]); printf("\n"); // добавление элементов в АВЛ-дерево T = MakeEmpty( NULL ); for( i = 0; i < maxnum; i++ ) T = Insert( a[i], T ); printf("\nВывод АВЛ-дерева\n"); printTree(T); //Поиск и вывод вершин уровня printf("\nВведите уровень дерева \n"); int Level, max; scanf("%d",&Level); printf("\nНа уровне %d всего найдено вершин %d\n", Level, topCount(T, Level)); WriteAt(T, Level); // удаление АВЛ-дерева T = MakeEmpty(T); free(a); getch(); return 0; } |
