Двудольные графы
Является ли двудольным графом
простая цепь?
дерево?
полный граф?
Докажите, что дерево является двудольным графом. Какие деревья являются полными двудольными графами.
В теннисном турнире каждый игрок команды «синих» встречается с каждым игроком команды «красных». Число игроков в командах одинаково и не более восьми. «Синие» выиграли в четыре раза больше встреч, чем «красные». Сколько человек в каждой из команд?
Школьники на кружке решали 16 задачи. Каждый из 16 школьников решил по четыре задачи, и каждая задача была решена четырьмя школьниками. Доказать, что можно организовать разбор задач так, чтобы каждый рассказал одну решенную им задачу и чтобы все задачи были разобраны.
Каждый из учеников 9 «А» класса дружит с тремя учениками 9 «Б» класса, а каждый из учеников 9 «Б» класса дружит с тремя учениками 9 «А» класса. Докажите, что число учеников в обоих классах одинаково.
Строительному управлению для выполнения работы требуются каменщик плотник, водопроводчик и слесарь. На эти должности имеются пять претендентов: один может работать каменщиком, другой – плотником, третий – каменщиком и водопроводчиком и еще двое имеют по две специальности – водопроводчика и слесаря. Можно ли охватить весь фронт работ (используя четверых рабочих)? Если да, то подробно проверьте выполнение условия теоремы Холла.
Десять кандидатов готовятся к двум космическим экспедициям на Марс. Поскольку экспедиции будут продолжаться несколько лет, а их участники окажутся в замкнутом пространстве небольшого объема, то большое значение приобретает психологическая совместимость членов экипажа. Путем тестирования установлены пары кандидатов, присутствие которых в одной и той же экспедиции было бы нежелательным. Результаты тестирования отражены в таблице. (Если на пересечении I строки j столбца находится знак «+», то участие I и j кандидатов в одной экспедиции нежелательно.) Разделите кандидатов на две группы для участия в экспедициях.
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
1
|
|
+
|
+
|
+
|
|
|
|
|
|
|
2
|
+
|
|
|
|
+
|
|
|
|
|
|
3
|
+
|
|
|
|
|
|
+
|
|
|
|
4
|
+
|
|
|
|
|
+
|
|
|
|
|
5
|
|
+
|
|
|
|
|
|
+
|
|
|
6
|
|
|
|
+
|
|
|
|
|
|
+
|
7
|
|
|
+
|
|
|
|
|
+
|
|
+
|
8
|
|
|
|
|
+
|
|
+
|
|
+
|
|
9
|
|
|
|
|
|
|
|
+
|
|
+
|
10
|
|
|
|
|
|
+
|
+
|
|
+
|
|
В школе 4 кружка: домоводство, математический кружек, компьютеный клуб и кружек английского языка. Пять человек из класса посещают эти кружки, причем один и тот же ученик может являться членом нескольких кружков. Можно ли выбрать старосту в каждом кружке так, чтобы ни один человек не был старостой сразу в двух кружках, в следующих случаях:
Кружок домоводства посещают 1, 3 и 4 ученики, математический кружок – 1, 4 и 5, компьютерный клуб – 2, 3 и 5, кружок английского языка – 2, 4 и 5.
Кружок домоводства посещают 1 и 3 ученики, математический кружок – 2 и 3, компьютерный клуб – 2 и 1, кружок английского языка – 3.
Кружок домоводства посещают 1, 3 и 4 ученики, математический кружок – 2 и 5, компьютерный клуб – 2 и 5, кружок английского языка – 2.
Ориентированные графы и мультиграфы
Решите задачу 35. Граф может быть орграфом или мультиграфом.
В некотором государстве каждый город соединен с каждым дорогой. Сумасшедший король хочет ввести на дорогах одностороннее движение, так чтобы, выехав из любого города, в него нельзя было вернуться. Можно ли так сделать?
Докажите, что на ребрах связного графа можно так расставить стрелки, чтобы из некоторой вершины можно было добраться по стрелкам до любой другой.
Доказать, что связный граф можно обойти, проходя по каждому ребру дважды.
Изобразите матрицы смежности и инциденций ориентированного графа:
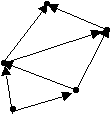
Дана матрица смежности. Изобразить граф, ей соответствующий.
а)
-
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
1
|
1
|
0
|
1
|
1
|
0
|
1
|
0
|
2
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
3
|
1
|
0
|
0
|
1
|
0
|
1
|
0
|
4
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
5
|
1
|
0
|
0
|
0
|
0
|
0
|
1
|
6
|
1
|
0
|
0
|
1
|
0
|
1
|
0
|
7
|
0
|
1
|
0
|
0
|
1
|
0
|
0
|
б)
-
|
1
|
2
|
3
|
4
|
5
|
1
|
1
|
2
|
0
|
0
|
1
|
2
|
0
|
0
|
3
|
0
|
0
|
3
|
0
|
0
|
2
|
1
|
0
|
4
|
1
|
0
|
1
|
0
|
1
|
5
|
1
|
0
|
0
|
0
|
0
|
Из города А в город В ведут несколько дорог (карта дорог на рисунке). Найдите число маршрутов из А в В, учитывая, что при движении необходимо всегда приближаться к В.
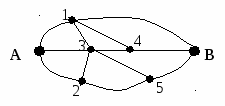 
Может ли в ориентированном графе полустепень захода каждой вершины быть равна 3, а полустепень исхода – 4?
В некоторой стране есть столица и еще 100 городов. Некоторые города (в том числе и столица) соединены дорогами с односторонним движением. Из каждого нестоличного города выходит 20 дорог, и в каждый такой город входит 21 дорога. Докажите, что в столицу нельзя проехать ни из одного города.
В некотором государстве 101 город. а) Каждый город соединен с каждым дорогой с односторонним движением, причем в каждый город входит 50 дорог и из каждого города выходит 50 дорог. Докажите, что из любого города можно доехать в любой другой, проехав не более чем по двум дорогам; б) Некоторые города соединены дорогами с односторонним движением, причем в каждый город входит 40 дорог и из каждого города выходит 40 дорог. Докажите, что из любого города можно добраться до любого другого, проехав не более чем по трем дорогам
В стране Ориентация на всех дорогах введено одностороннее движение, причем из любого города в любой другой можно добраться, проехав не более чем по двум дорогам. Одну дорогу закрыли на ремонт так, что из каждого города по-прежнему можно добраться до каждого. Докажите, что для любых двух городов это можно сделать, проехав не более, чем по трем дорогам.
Найдите компоненты сильной связности графа, заданного матрицей смежности:
-
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
1
|
0
|
1
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
2
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
3
|
0
|
1
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
4
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
5
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
6
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
7
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
8
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
9
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
Найдите компоненты сильной связности графа:
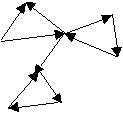
Решите задачу 62, считая, что заданы матрицы смежности ориентированного графа.
Дана матрица смежности графа, определить, является ли он эйлеровым. Ответ обоснуйте.
-
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
1
|
0
|
1
|
1
|
0
|
0
|
0
|
1
|
2
|
0
|
0
|
1
|
0
|
1
|
0
|
0
|
3
|
0
|
1
|
0
|
0
|
0
|
0
|
1
|
4
|
1
|
0
|
0
|
0
|
1
|
1
|
0
|
5
|
1
|
0
|
0
|
1
|
0
|
0
|
0
|
6
|
1
|
0
|
0
|
1
|
0
|
0
|
0
|
7
|
0
|
0
|
0
|
1
|
0
|
1
|
0
|
На ребрах связного графа расставлены стрелки так, что для каждой вершины числа входящих и выходящих ребер равны. Докажите, что двигаясь по стрелкам, можно добраться от любой вершины до любой другой.
По заданной матрице весов графа G найти величину минимального пути и сам путь от вершины 1 до вершины 6 по алгоритму Дейкстры, а затем величину максимального пути и сам путь между теми же вершинами:
|
1
|
2
|
3
|
4
|
5
|
6
|
1
|
-
|
6
|
8
|
11
|
10
|
∞
|
2
|
∞
|
-
|
∞
|
9
|
7
|
15
|
3
|
∞
|
8
|
-
|
7
|
14
|
11
|
4
|
∞
|
∞
|
∞
|
-
|
6
|
7
|
5
|
∞
|
∞
|
∞
|
∞
|
-
|
9
|
6
|
∞
|
∞
|
∞
|
∞
|
∞
|
-
|
|
1
|
2
|
3
|
4
|
5
|
6
|
1
|
-
|
5
|
8
|
7
|
18
|
∞
|
2
|
∞
|
-
|
11
|
∞
|
∞
|
∞
|
3
|
∞
|
∞
|
-
|
∞
|
∞
|
17
|
4
|
∞
|
10
|
12
|
-
|
6
|
∞
|
5
|
∞
|
7
|
8
|
∞
|
-
|
11
|
6
|
∞
|
∞
|
∞
|
∞
|
∞
|
-
|
|
1
|
2
|
3
|
4
|
5
|
6
|
1
|
-
|
5
|
10
|
13
|
∞
|
∞
|
|
∞
|
-
|
8
|
9
|
13
|
∞
|
3
|
∞
|
∞
|
-
|
5
|
3
|
6
|
4
|
∞
|
∞
|
∞
|
-
|
8
|
10
|
5
|
∞
|
∞
|
∞
|
∞
|
-
|
9
|
6
|
∞
|
∞
|
∞
|
∞
|
∞
|
-
|
В связном неориентированном графе степени всех вершин четны. Докажите, что на ребрах этого графа можно расставить стрелки так, чтобы выполнялись следующие условия: а) двигаясь по стрелкам, можно добраться от любой вершины до любой другой; б) для каждой вершины числа входящих и выходящих ребер равны.
На плоскости отмечено некоторое конечное число точек. Некоторые пары точек являются началами и концами векторов, причем число векторов, выходящих из любой точки равно числу входящих в неё. Найдите сумму векторов.
В некоторой стране каждый город соединен с каждым дорогой с односторонним движением. Докажите, что найдется город, из которого можно добраться в любой другой.
Несколько команд сыграли между собой круговой турнир по волейболу. Будем говорить, что команда А сильнее команды В, если либо А выиграла у В, либо существует команда С такая, что А выиграла у С, а С - у В. а) Докажите, что есть команда, которая сильнее всех. б) Докажите, что команда, выигравшая турнир, сильнее всех.
В одном государстве 100 городов, и каждый соединен с каждым дорогой с односторонним движением. Докажите, что можно поменять направление движения на одной дороге так, чтобы от любого города можно было доехать до любого другого.
20 команд сыграли круговой турнир по волейболу. Докажите, что команды можно занумеровать числами от 1 до 20 так, что 1-я команда выиграла у 2-й, 2-я - у 3-й, ..., 19-я у 20-й.
Докажите, что если победитель турнира по волейболу, проведенного по круговой системе, проиграл команде В, то существует команда С, выигравшая у В, у которой выиграл победитель.
Какие-то две команды набрали в круговом волейбольном турнире одинаковое число очков. Докажите, что найдутся команды А, В и С такие, что А выиграла у В, В выиграла у С, а С выиграла у А.
Плоские графы
Проверить формулу Эйлера для графов W6 и К2 n.
Для шахматной доски размером К х К найдите числа p, q, r и убедитесь в справедливости теоремы Эйлера.
Обобщите формулу Эйлера для несвязных графов.
В стране Озерная 7 озер, соединенных между собой 10 каналами, причем от любого озера можно доплыть до любого другого. Сколько в этой стране островов?
Мэрия решила построить в каждом квартале города, имеющего 155 перекрестков и 260 отрезков улиц между перекрестками, универсам. Сколько будет построено универсамов?
К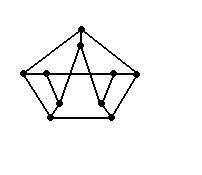 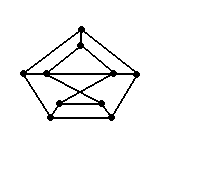 акие из графов являются планарными: акие из графов являются планарными:
Докажите, что, если в планарном графе каждая грань есть Сn (цикл длины n), q=n*(p-2)/(n-2).
В квадрате отметили 20 точек и соединили их непересекающимися отрезками друг с другом и с вершинами квадрата так, что квадрат разбился на треугольники. Сколько получилось треугольников?
При каких n графы порядка 2n являются планарными?
Печатная плата представляет собой пластинку из изолирующего материала, в специально изготовленные гнезда которой устанавливают электронные приборы. В качестве проводников, соединяющих эти приборы, служат напыленные металлические дорожки. Поскольку проводники не изолируются, то дорожки не должны пересекаться. Если это может произойти, то одну из дорожек переносят на другую сторону платы. Конструктор Иванов придумал схему печатной платы, которая состоит из 12 приборов и 32 проводников, соединяющих их. Можно ли изготовить такую плату так, что все проводники будут расположены на одной её стороне?
Докажите, что для плоского связного графа справедливо неравенство q<=3p-6
Докажите, что граф, имеющий 5 вершин, каждая из которых соединена ребром с любой другой, не является плоским.
Можно ли построить три дома, вырыть три колодца и соединить тропинками каждый дом с каждым колодцем так, чтобы тропинки не пересекались?
Докажите, что для любого плоского графа (в том числе и несвязного) справедливо неравенство q<=3p-6.
Докажите, что граф, имеющий 10 вершин, степень каждой из которых равна 5, - не плоский.
В графе степень любой вершины не меньше шести. Доказать, что его нельзя нарисовать на плоскости, так чтобы никакие два ребра его не пересекались.
Каждое ребро полного графа с 11 вершинами покрашено в один из двух цветов: красный или синий. Докажите, что либо «красный'», либо «синий» граф не является плоским.
Покажите, что граф W6 стягиваем к графу К4.
Докажите, что граф Петерсона не является планарным.
Инженер Иванов усовершенствовал свою плату. Теперь она имеет 9 приборов и 17 проводников. Схема платы представлена на рисунке. Можно ли изготовить такую плату так, что все проводники будут расположены на одной её стороне?
С 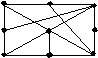 тереографическая проекция
Докажите, что число вершин (p), ребер (q) и граней (r) любого выпуклого многогранника связано формулой p–q+r=2.
Доказать, что граф правильного многогранника является плоским и правильным.
Найти гамильтоновы циклы на правильных графах.
При изготовлении некоторой однослойной печатной платы по технологическим условиям один заданный проводник должен находится на краю платы. Доказать, что это всегда можно сделать.
Н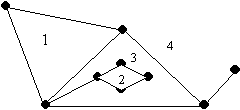 арисуйте граф, изоморфный графу, изображенному на рисунке, так, чтобы внешней стала грань арисуйте граф, изоморфный графу, изображенному на рисунке, так, чтобы внешней стала грань
Двойственные графы
Найдите двойственные графы для следующих графов:
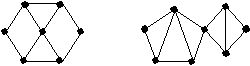
Покажите, что граф, двойственный к колесу Wn, является колесом.
Плоский граф G имеет 7 вершин, 10 ребер и 5 граней. Сколько вершин, ребер и граней имеет двойственный к нему граф.
Докажите, что у выпуклого многогранника найдутся две грани с одинаковым числом ребер.
Докажите, что не существует выпуклого многогранника, у которого все грани шестиугольники.
Может ли существовать плоский граф с пятью гранями, в котором каждая пара граней является смежными?
Дан плоский граф, в каждой вершине которого сходится не более трех ребер. Докажите, что
четное число граней имеет нечетное число смежных граней;
существует грань, которая имеет не более пяти смежных с ней граней.
Раскраски графа
Найдите хроматические числа для:
вполне несвязного графа с n вершинами;
полного графа с n вершинами;
двудольного графа, доли которого имеют n и m вершин;
дерева с n вершинами.
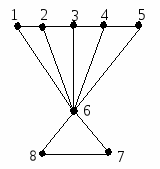
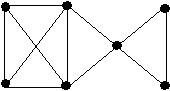
Для графов, изображенных на рисунке, найдите хроматические числа и какую-либо правильную раскраску.
Сколькими способами можно раскрасить полный помеченный граф на 6 вершинах шестью цветами? (Два способа считаются различными, если некоторая вершина при одном способе имеет один цвет, а при другом способе – другой.)
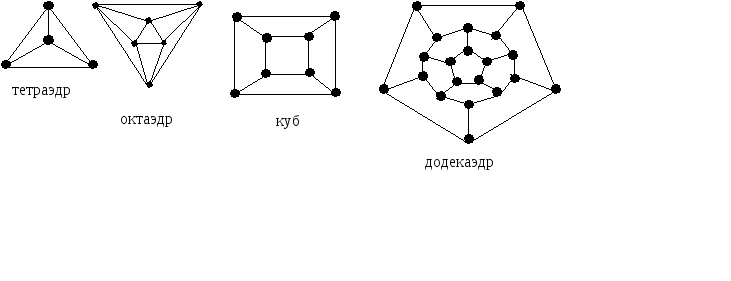
Определите хроматические числа для графов платоновых тел:
Приведите пример графа, последовательная раскраска вершин которого не является минимальной.
Коробка скоростей – механизм для изменения частоты вращения ведомого вала при неизменной частоте вращения ведущего. Это изменение происходит за счет того, что находящиеся внутри коробки шестерни вводятся в зацепление специальным образом. Одна из задач, стоящих перед конструктором коробки, заключается в минимизации числа валов, на которых размещаются шестерни.
Некоторые шестерни не должны находиться на одном валу, например, они могут быть в зацеплении или их общий вес велик для одного вала, и т.д. В таблице крестиками указаны такие пары шестерен. Найдите минимальное число валов, на которые можно поместить шестерни.
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
1
|
|
+
|
|
+
|
+
|
|
+
|
2
|
+
|
|
+
|
|
+
|
|
+
|
3
|
|
+
|
|
|
+
|
+
|
|
4
|
+
|
|
|
|
|
+
|
|
5
|
+
|
+
|
+
|
|
|
|
+
|
6
|
|
|
+
|
+
|
|
|
+
|
7
|
+
|
+
|
|
|
+
|
+
|
|
Образовавшийся коммерческий университет арендует здание для проведения занятий. В четверг проводится 7 лекций: право, английский язык, французский язык, экономика, менеджмент, маркетинг, этикет. Чтение каждой лекции в отдельности занимает один час, но некоторые лекции не могут читаться одновременно. В таблице крестиком помечены лекции, которые не могут читаться одновременно. Определите минимальное время, за которое могут быть прочитаны лекции в четверг.
-
|
П
|
А
|
Ф
|
Э
|
М
|
М
|
Э
|
Право
|
|
+
|
|
+
|
|
|
+
|
Англ. яз.
|
+
|
|
+
|
|
+
|
+
|
|
Фран. яз.
|
|
+
|
|
|
+
|
+
|
+
|
Экономика
|
+
|
|
|
|
+
|
+
|
|
Менеджмент
|
|
+
|
+
|
+
|
|
+
|
|
Маркетинг
|
|
+
|
+
|
+
|
+
|
|
|
Этикет
|
+
|
|
+
|
|
|
|
| |
 Скачать 2.66 Mb.
Скачать 2.66 Mb.



 тереографическая проекция
тереографическая проекция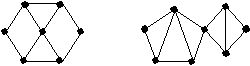





 акие из графов являются планарными:
акие из графов являются планарными: арисуйте граф, изоморфный графу, изображенному на рисунке, так, чтобы внешней стала грань
арисуйте граф, изоморфный графу, изображенному на рисунке, так, чтобы внешней стала грань