Учебник по дискретной математики. Д. Ушинского Дискретная математика
 Скачать 2.66 Mb.
|
|
3 свойство – основное свойство  Доказательство. 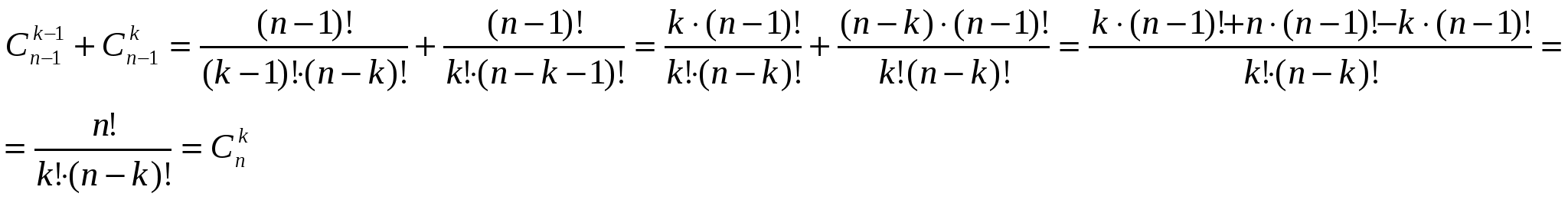 Комбинаторное доказательство. Составим k-сочетание из n элементов а1, а2, …,an и разобьем их на два класса. В первый из них войдут сочетания, содержащие элемент an, во второй – не содержащие этого элемента. Если из любого сочетания первого класса откинуть элемент аn, то останется (к –1)-сочетание, составленное из элементов а1, а2, …, an-1. Число таких сочетаний равно  . Поэтому в первый класс входит комбинаций. Сочетания второго класса являются k-сочетаниями, составленными из элементов а1, а2, …,an-1. Поэтому их число равно  . Поскольку любое k-сочетание принадлежит одному и только одному из этих классов, а общее число этих сочетаний равно  , то, используя правило сложения, приходим к искомому равенству.4 свойство:  Комбинаторное доказательство. 2n – число всех размещений с повторениями из элементов двух типов. Разобьем эти размещения на классы, отнеся в k-ый класс те, в которые входят k элементов первого типа и n–k элементов второго типа. Размещения k-го типа - это ни что иное, как всевозможные перестановки из k элементов первого типа и n–k элементов второго типа. Число таких перестановок равно P(k, n–k)=C(n, k). По правилу суммы общее число размещений всех классов равно  . С другой стороны, это же число равно 2n.5 свойство:  Комбинаторное доказательство. Выпишем все сочетания из n элементов а1, …,аn и сделаем следующее преобразование: к сочетанию, не содержащему элемент а1, допишем его, а из сочетаний, куда оно входит, вычеркнем. Легко проверить, что при этом снова получаются все сочетания, и притом по одному разу. Но при этом преобразовании все сочетания, имевшие четное число элементов, превратятся в сочетания, имеющие нечетное число элементов, и обратно. Значит сочетаний с четным и нечетным количеством элементов одинаковое количество (пустое сочетание тоже входит в рассмотрение). Это и выражает данная формула. Задача. На окружности отмечено 11 точек. Сколько существует многоугольников с вершинами в отмеченных точках? Решение. Первый способ. Существует  треугольников с вершинами в отмеченных точках,  – четырехугольников,  – пятиугольников, … ,  – одиннадцатиугольников. Таким образом, по правилу суммы всего многоугольников +++…+. Из четвертого свойства следует, что это выражение равно 211- - =1 982.Второй способ. Любая из одиннадцати точек либо является вершиной рассматриваемого многоугольника, либо не является. Всего вариантов 211. Но одна или две точки не могут составлять многоугольник. Остается 211- - вариантов многоугольников с вершинами в отмеченных точках.Сочетания с повторениями. Задача. В кондитерском магазине продавались 4 сорта пирожных: наполеоны, эклеры, песочные и слоеные. Сколькими способами можно купить 7 пирожных? Решение Эта задача не является задачей на размещения с повторениями, так как порядок, в котором укладывают пирожные в коробку, несуществен. Поэтому она ближе к задачам на сочетания. Но от задач на сочетания она отличается тем, что в комбинации могут быть повторяющиеся элементы. Такие задачи называют задачами на сочетания с повторениями. Чтобы решить задачу, поступим следующим образом. Зашифруем каждую покупку с помощью нулей и единиц. Сначала напишем столько единиц, сколько куплено наполеонов. Потом, чтобы отделить наполеоны от эклеров, напишем нуль, затем – столько единиц, сколько куплено эклеров, и т. д. Например, если куплено 3 наполеона, 1 эклер, 2 песочных и 1 слоеное пирожное, то получим такую запись: 1110101101. Ясно, что разным покупкам соответствуют разные комбинации из 7 единиц и 3 нулей. Обратно, каждой комбинации 7 единиц и 3 нулей соответствует какая-то покупка. Таким образом, число различных покупок равно числу перестановок с повторениями, которые можно составить из 7 единиц и 3 нулей. А это число равно P(7,3)=120. К тому же самому результату можно было прийти и другим путем, а именно: расположим в каждой покупке пирожные в таком порядке: наполеоны, эклеры, песочные и слоеные, а потом перенумеруем их. Но при нумерации будем к номерам эклеров прибавлять 1, к номерам песочных – 2, к номерам слоеных – 3. К номерам наполеонов ничего прибавлять не будем. Например, пусть куплено 2 наполеона, 3 эклера, 1 песочное пирожное и 1 слоеное. Тогда эти пирожные нумеруются так: 1, 2, 4, 5, 6, 8, 10. Ясно, что самый большой номер может быть 10, самый маленький – 1, а кроме того, ни один из номеров не повторяется, причем они образуют возрастающую последовательность. Обратно, каждой возрастающей последовательности из 7 чисел соответствует некоторая покупка. Например, последовательность 2, 3, 4, 5, 7, 8, 9 соответствует покупке из 4 эклеров и 3 песочных пирожных. Чтобы убедиться в этом, надо отнять от заданных номеров числа 1, 2, 3, 4, 5, 6, 7. Мы получим числа 1, 1, 1, 1, 2, 2, 2. Но 1 мы прибавляли к номерам эклеров, а 2 – к номерам песочных. Отсюда, общее число покупок равно числу возрастающих последовательностей из 7 чисел от 1 до 10. А число таких последовательностей равно C(10,7)=120. Сочетаниями с повторениями из n элементов по k называют всевозможные комбинации, составленные из элементов n видов по k элементов в каждой. Комбинации считаются различными, если они отличаются составом, но не порядком входящих в них элементов. В комбинацию могут входить элементы одного вида. Количество сочетаний с повторениямиизn элементов по k обозначают  . Общее правило вычисления количества сочетаний с повторениями:  Доказательство. Зашифруем каждую комбинацию с помощью нулей и единиц: для каждого типа напишем столько единиц, сколько предметов этого типа входит в комбинацию, а предметы различных типов отделить нулями. При этом число единиц будет k, а число нулей – n–1. Различным комбинациям будут соответствовать различные перестановки с повторениями из k элементов первого вида и n–1 элементов второго вида, а каждой перестановке с повторениями – своя комбинация. Итак,  .Встречаются задачи, в которых на сочетания с повторениями накладывается дополнительное условие, например, когда в комбинацию обязательно должны входить элементы r фиксированных типов, где r≤n. Эта задача легко сводится к уже решенной. Для того чтобы обеспечить присутствие заданных r типов, возьмем с самого начала по одному элементу каждого такого типа. Тем самым в k-сочетании окажутся заняты r мест. Поэтому ответом на задачу будет число  . В частности, если требуется, чтобы в каждом сочетании был элемент каждого из типов (n≤k), то получится  .Задача. Сколько существует различных бросаний двух одинаковых кубиков? Решение. Переформулируем задачу. Всего при подбрасывании одного кубика возможны шесть ситуаций – имеем предметы шести различных типов. Подбрасывают два кубика, следовательно, из данных шести типов предметов необходимо выбрать два, причем нас не интересует порядок выбора, и допускается выбор одинаковых предметов. Таким образом, это задача на сочетания с повторением. По формуле для вычисления количества сочетаний с повторением имеем  различных бросаний двух одинаковых кубиков.Комбинаторика разбиений Многим комбинаторным задачам можно придать вид стандартной схемы. В этой схеме объекты (предметы) помещаются в ящики. Из-за наложения различных ограничений получаются различные задачи. Рассмотрим некоторые из них. Имеется n1 предметов одного сорта, n2 – другого, ... , nk – k-го сорта. Сколькими способами можно разложить их в два ящика? Так как в каждый ящик может попасть от 0 до ni предметов i-го сорта (во второй все оставшиеся), по правилу произведения получаем (n1+1)∙(n2+1)∙...∙(nk+1) способов раскладки. Задача. Двое ребят собрали 10 ромашек, 15 васильков и 14 незабудок. Сколькими способами они могут разделить эти цветы? Решение. Необходимо 10 предметов одного вида, 15 – второго и 14 – третьего разложить в два ящика. Применяя рассуждения, аналогичные приведенным выше, получаем 111615=2460 способов раздела цветов. Следствие 1. Если все предметы различны (n1=n2=...=nk=1), то их можно разложить 2k способами. Следствие 2. Если в каждый ящик нужно положить не менее si предметов i-го сорта, то получим формулу: (n1-2s1+1) (n2-2s2+1) ... (nk-2sk+1). Даны n различных предметов и k ящиков. Надо положить в первый ящик n1 предметов, во второй – n2, ..., в k-ый – nk, где n1+...+nk=n. Сколькими способами можно сделать такое распределение, если не интересует порядок предметов в ящике? Выложим все предметы в один ряд. Это можно сделать n! способами. Первые n1 предметов положим в первый ящик, вторые n2 предмета – во второй ящик, …, k-ые nk предметов – в к-ый ящик. Так как нас не интересует порядок предметов в ящике, то любая перестановка первых n1 предметов не меняет результат раздела. Точно так же его не меняет любая перестановка вторых n2 предметов, ..., k-ых nk предметов. По правилу произведения получаем n1! n2!...nk! перестановок, не меняющих результата раздела. Таким образом, n! перестановок делятся на группы по n1! n2!...nk! перестановок в каждой группе, причем перестановки из одной группы приводят к одинаковому распределению предметов. Следовательно, число раздела предметов равно  =P(n1,...,nk).Задача. При игре в домино 4 игрока делят поровну 28 костей. Сколькими способами они могут это сделать? Решение. Переформулируем задачу: необходимо разложить 28 предметов в 4 ящика по 7 предметов в каждый, причем порядок предметов в ящике не важен. Получаем  способов распределения костей домино.Можно было рассуждать другим способом. Первый игрок выбирает себе 7 костей из 28, это можно сделать  способами. Второму необходимо выбрать 7 костей из оставшихся 21, это можно сделать  способами. Третьему 7 из 14 –  способов. А четвертый заберет оставшиеся. По правилу произведения получаем  .Даны n различных предметов и k одинаковых ящика. Надо положить в каждый ящик n1 предметов, где n1=  . Сколькими способами можно сделать такое распределение, если не интересует порядок предметов в ящике, и все ящики одинаковы?Задача отличается от предыдущей только тем, что ящики не пронумерованы. Так как k ящиков можно переставить k! способами, то полученный в предыдущей задаче результат необходимо разделить на k!. Всего  способов распределения.Задача. Сколькими различными способами можно разделить 8 книг на 4 бандероли по 2 книги в каждой? Решение. Если бы интересовал порядок бандеролей, то существовало бы  способов распределения книг. Так как не важно, в каком порядке будут отправлены бандероли, то полученное число необходимо поделить на 4!. Итого  способов разделить 8 книг на 4 бандероли по 2 книги.Сколькими способами можно разложить n одинаковых предметов в k ящиков? Выложим все предметы в один ряд, добавим к ним k–1 одинаковых разделяющих предмета. Переставим всеми возможными способами n данных одинаковых предметов и k–1 разделяющих. Каждая такая перестановка определяет один из способов распределения. А именно предметы, расположенные до первого разделителя, положим в первый ящик, предметы, расположенные между первым и вторым разделителем, – во второй ящик и так далее, предметы расположенный после k–1 разделителя, – в k ящик. По формуле перестановок с повторениями число таких перестановок равно P(n, k-1)=  . Значит, всего имеем способов разложить n одинаковых предметов в k ящиков.Задача. Трое ребят собрали с яблони 40 яблок. Сколькими способами они могут их разделить, если все яблоки считаются одинаковыми (то есть нас интересует, сколько яблок получит каждый, а не какие именно)? Решение. Добавим два разделяющих предмета, тогда получаем Р(40, 2)=780 способа разделить яблоки. Следствие 1. Если в каждый ящик надо положить не менее r предметов, то получим: P(n-kr,k-1) способов. Следствие 2. Если в каждый ящик надо положить хотя бы один предмет, то r=1 и получим P(n-k,k-1)=  способов распределения.Сколько существует способов разложить n различных предметов в k ящиков, если нет никаких ограничений? Каждый предмет можно положить в любой из k ящиков. Получаем kn способов распределения предметов по ящикам. Задача. Сколькими способами можно разделить 8 различных пирожных между 5 детьми? Решение. Необходимо разложить 8 предметов по 5 ящикам. Это можно сделать 58=390 625 способами. Сколькими способами можно поместить n различных предметов в k ящиков, если не должно быть пустых ящиков? Данные r ящиков остаются пустыми, если в k–r ящиков предметы кладутся без ограничений. r пустых ящиков можно выбрать Cnk способами. В оставшиеся k–r ящиков предметы можно разложить (k–r)n способами. По формуле включений и исключений число распределений, при которых хотя бы один ящик остается пустым, равно  . Тогда количество распределений, при которых ни один ящик не окажется пустым, равно kn-( ).Задача. Сколькими способами можно послать по почте 8 различных фотографий, использовав 5 конвертов? Разбор. Переформулируем задачу: необходимо 8 предметов разложить в 5 ящиков. Посылать пустые конверты не рационально, поэтому накладывается запрет на пустые ящики. Применяя полученную выше формулу, получаем 58-  48+ 38- 28+  18=126 020.Имеется n1 предметов одного сорта, n2 – другого, ... , ns – s-го сорта. Сколькими способами их можно разложить по k ящикам, если не должно быть пустых ящиков? Применяя рассуждения, аналогичные предыдущей задаче, получим следующую формулу  . |