Исследование динамики поступательно вращательного движения твёрдого тела. Дана точка А. Построить эпюр точки В, симметричной точке А, относительно плоскостей проекций горизонтальной, вертикальной и профильной (всего 3 чертежа)
 Скачать 0.93 Mb. Скачать 0.93 Mb.
|
|
Дана точка А. Построить эпюр точки В, симметричной точке А, относительно плоскостей проекций: горизонтальной, вертикальной и профильной (всего 3 чертежа).
Дана точка A. Построить эпюр точки В, симметричной точке А, относительно оси проекций Оx, Оy, Oz.
В заданной плоскости (ABC) построить через точку А горизонталь, через точку В - фронталь.
Задача 4. Построить линию пересечения треугольников АВС и DЕК и показать видимость их в проекциях.
Задача 1. Дана точка А (–15, –24, –15). Построить эпюр точки В, симметричной точке А, относительно плоскостей проекций: горизонтальной, вертикальной и профильной. 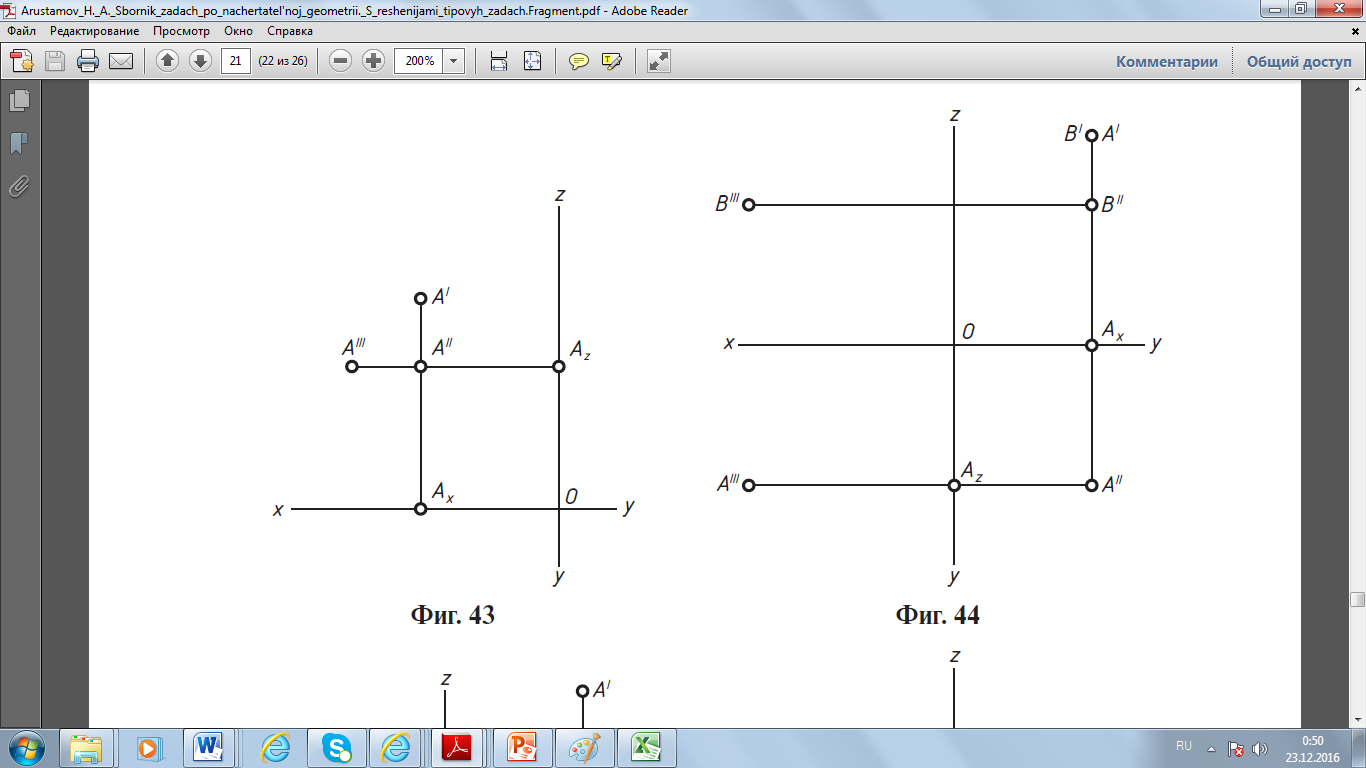 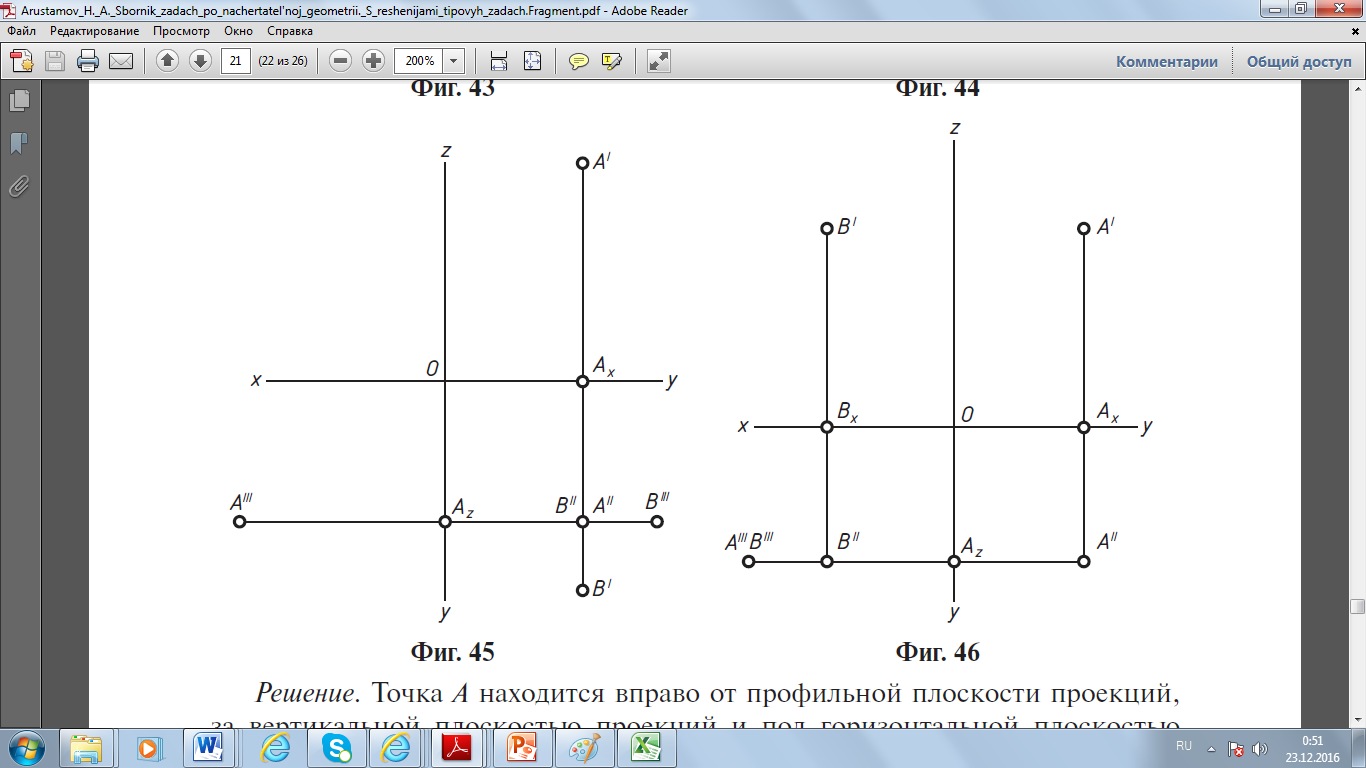  Решение. Точка А находится вправо от профильной плоскости проекций, за вертикальной плоскостью проекций и под горизонтальной плоскостью проекций, т.е. в седьмом октанте. Строим ее эпюр. Откладываем на отрицательной оси Оx отрезок ОAx длиной 15 мм (х) и, проведя через точку Ax прямую перпендикулярно оси Оx, откладываем на ней отрезки вверх AxA' длиной 24 мм (у) и вниз AxA'' длиной 15 мм (z). Затем проводим через точку A'' прямую перпендикулярно оси Oz и откладываем влево отрезок AzA''' длиной 24 мм (у). 1. Точка В, симметричная данной точке относительно горизонтальной плоскости проекций, находится в шестом октанте, т.е. В (–15, –24, 15). Откладываем на общем перпендикуляре вверх отрезки AxB' длиной 24 мм (у) и AxB'' длиной 15 мм (z) и затем находим профильную проекцию (B''' ) точки В. 2. Точка В, симметричная данной точке относительно вертикальной плоскости проекций, находится в восьмом октанте, т.е. В (–15, 24, –15). Построив, как и выше, эпюр точки А, откладываем на общем перпендикуляре вниз отрезки AxB' длиной 24 мм (у) и AxB'' длиной 15 мм (z). Затем, проведя через точку B'' перпендикулярно оси Oz прямую, откладываем на ней вправо отрезок AzB''' длиной 24 мм (у). 3. Точка В, симметричная данной точке относительно профильной плоскости проекций, находится в третьем октанте, т.е. В (15, –24, –15). Построив, как и выше, эпюр точки А, откладываем на положительной оси Оx отрезок OBx длиной 15 мм (x) и, проведя через точку Bx прямую перпендикулярно оси Оx, откладываем на ней отрезки вверх BxB' длиной 24 мм (у) и вниз BxB'' длиной 15 мм (z). Затем находим профильную проекцию (B''') точки В. Задача 2. Дана точка A (15, 24, –15). Построить эпюр точки В, симметричной точке А, относительно оси проекций Оx, Оy, Oz. Решение. Точка А находится влево от профильной плоскости проекций перед вертикальной плоскостью проекций и под горизонтальной плоскостью проекций, т.е. в четвертом октанте. Строим ее эпюр. Откладываем на положительной оси Оx отрезок OAx длиной 15 мм (х) и, проведя через точку Ax прямую перпендикулярно оси Оx, откладываем на ней вниз отрезки AxA' длиной 24 мм (у) и AxA'' длиной 15 мм (z). Затем находим профильную проекцию (A''' ) точки А. 1. Точка В, симметричная данной точке относительно оси Оx, находится во втором октанте, т.е. В (15, –24, 15). Откладываем на общем перпендикуляре вверх отрезки AxB' длиной 24 мм (у) и AxB'' длиной 15 мм (z). Затем находим профильную проекцию (B''' ) точки В. 2. Точка В, симметричная данной точке относительно оси Oy, находится в пятом октанте, т.е. В (–15, 24, 15). Построив, как и выше, эпюр точки A, откладываем на отрицательной оси Оx отрезок OBx длиной 15 мм (х) и, проведя через точку Bx прямую перпендикулярно оси Оx, откладываем на ней отрезки вниз BxB' длиной 24 мм (у) и вверх BxB'' длиной 15 мм (z). Затем находим профильную проекцию (B''' ) точки В. 3. Точка В, симметричная данной точке относительно оси Oz, находится в седьмом октанте, т.е. В (–15, –24, –15). Построив, как и выше, эпюр точки A, откладываем на отрицательной оси Оx отрезок ОBx длиной 15 мм (х) и, проведя через точку Bx прямую перпендикулярно оси Оx, откладываем на ней отрезки вверх BxB' длиной 24 мм (у) и вниз BxB'' длиной 15 мм (z). Затем находим профильную проекцию (B''' ) точки В. 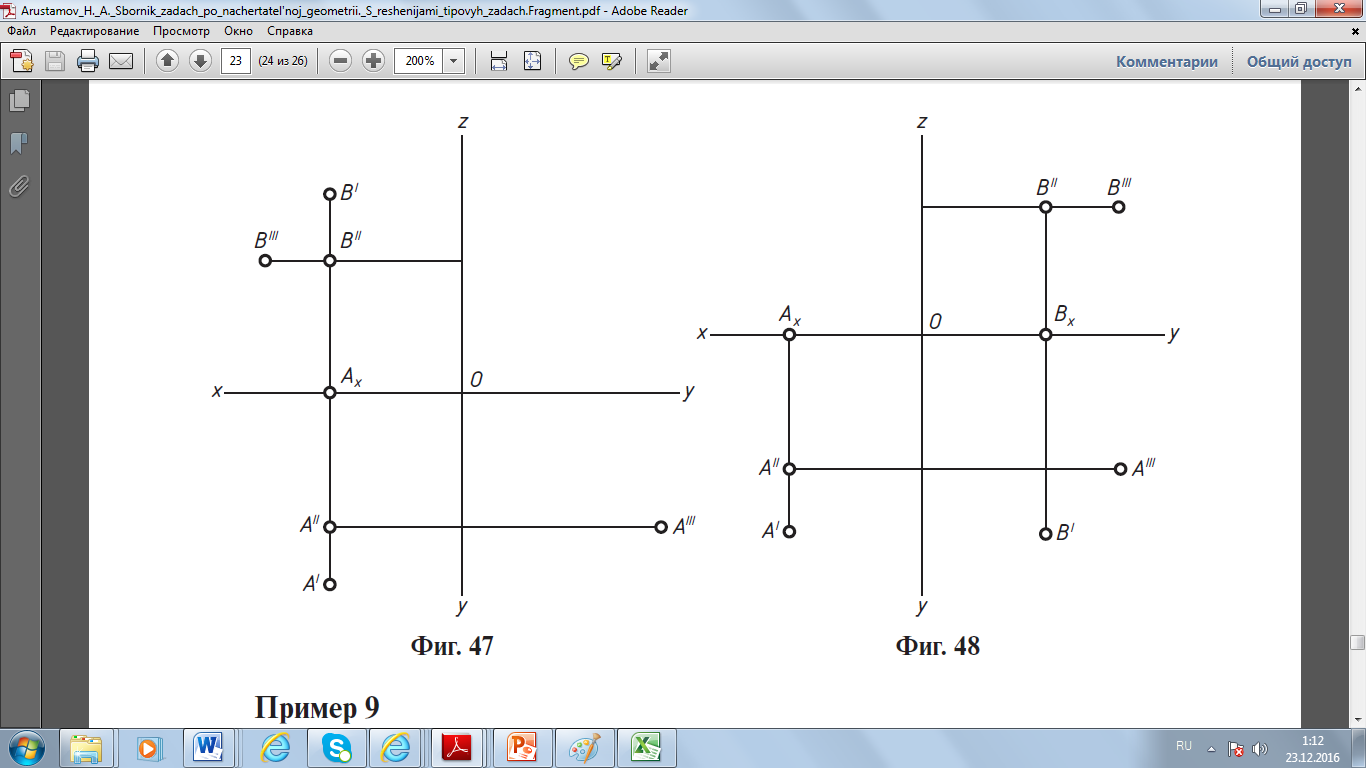  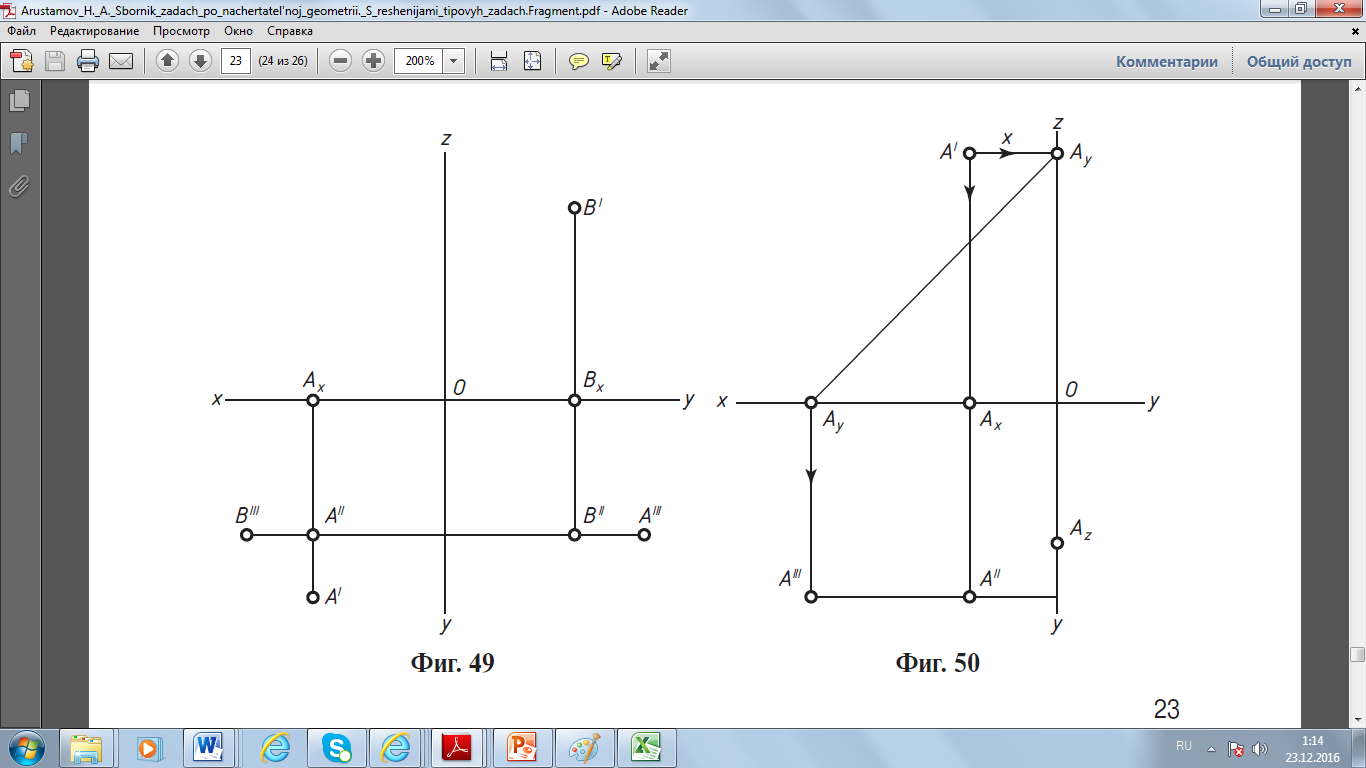 Задача 4. Указания к решению. В левой половине листа наметить оси координат и из табл.1 согласно своему варианту взять координаты точек А, В, С, D, Е, К вершин треугольников. Пример построения горизонтальной А1 и фронтальной А2 проекций точки А приведен на рис. 2. Аналогично построить проекции остальных вершин треугольников. 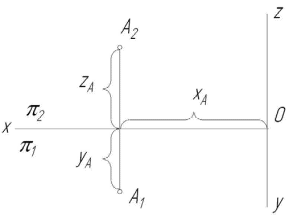 рис. 2 рис. 2Стороны треугольников и другие вспомогательные прямые провести вначале тонкими сплошными линиями (рис. 3). Линию пересечения треугольников строят по точкам М и N пересечения сторон одного треугольника с плоскостью другого треугольника, используя вспомогательные секущие проецирующие плоскости γ и β. 1.1. Одну из сторон треугольников, например прямую АВ (рис. 3), заключить в горизонтально проецирующую плоскость γ (след h1γ). Плоскость γ пересекает плоскость треугольника DЕК по прямой, горизонтальная проекция которой определяется проекциями точек 11 и 21. 1.2. На пересечении фронтальных проекций прямых 1222 и А2В2 получить фронтальную проекцию точки М2, принадлежащей линии пересечения треугольников. Горизонтальная проекция М1 лежит на горизонтальной проекции А1В1. 1.3. Для определения точки N (рис. 3), принадлежащей линии пересечения треугольников, прямую DК заключить во вспомогательную фронтально проецирующую плоскость β (след f2β). Фронтальная проекция линии пересечения плоскости β с плоскостью треугольника АВС определяется проекциями точек 32 и 42. На пересечении горизонтальных проекций прямых 3141 и D1К1 получить горизонтальную проекцию N1. Ее фронтальная проекция N2 лежит на фронтальной проекции D2К2. Если при построении линии пересечения горизонтальная проекция 3141 не пересекает D1К1 в пределах наложения горизонтальных проекций треугольников А1В1С1 и D1Е1К1, то все построения повторить, заключив во вспомогательную плоскость другую сторону треугольника. 1.4. Соединяя одноименные проекции точек М и N, получить проекции линии пересечения треугольников АВС и DЕК. Видимость сторон треугольника определить способом конкурирующих точек, выбранных на скрещивающихся прямых. Чтобы определить видимость на фронтальную плоскость проекций, на рис. 1 рассмотрены точки 5 и 6 (5 ∈ АВ, 6 ∈ ЕК). Фронтальные проекции точек совпадают: 52 ≡ 62 ; на горизонтальной проекции 51 ∈ А1В1 расположена дальше от плоскости π2, следовательно, в месте совпадения проекций конкурирующих точек точка 5 закрывает точку 6, а проекция А2В2 закрывает Е2К2. При определении видимости на горизонтальной плоскости проекций проанализировано расположение конкурирующих точек 7 и 8. Видимые отрезки сторон треугольников выделить сплошными толстыми линиями, невидимые показать штриховыми. 1 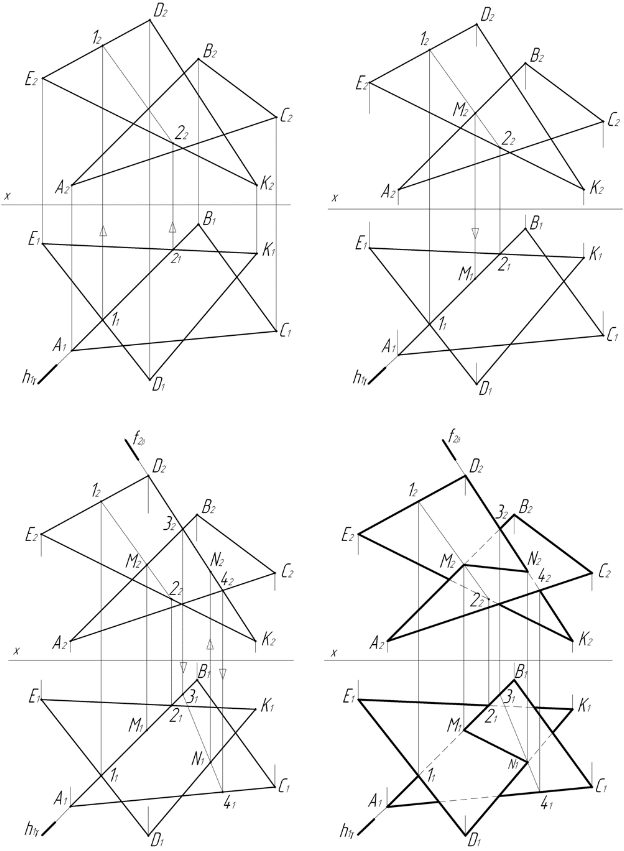 .1 1.2. .1 1.2.1.3. 1.4. 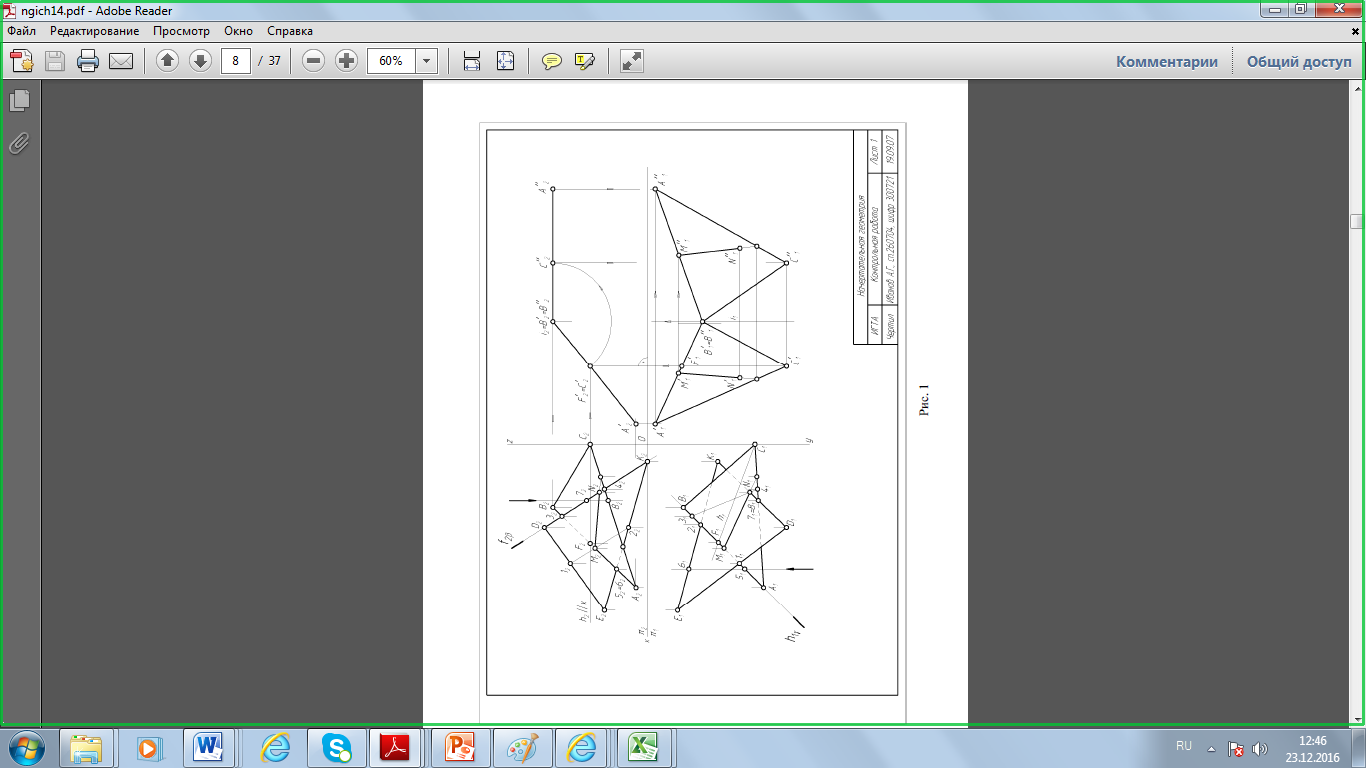 рис. 1 |
