_Даниэль Канеман, Думай медленно. Даниэль Канеман Думай медленно решай быстро

• Название: Даниэль Канеман Думай медленно решай быстро
• Дата: 14.09.2022
• Размер: 2.51 Mb.
• Имя файла: _Даниэль Канеман, Думай медленно.doc
• Тип: Реферат; #677778
• страница: 120 из 126

   Психофизика шанса

   До сих пор наше обсуждение шло в рамках правила ожидания Бернулли, согласно которому ценность (полезность) неопределенной перспективы образуется сложением полезностей возможных исходов, каждый из которых взвешен по его вероятности. Чтобы проверить это допущение, снова обратимся к психофизическим соображениям. Взяв ценность статус-кво за ноль, представим денежный подарок – скажем, 300 долларов – и определим его ценность. Теперь представьте, что получили в сего лишь билет лотереи, в которой разыгрывается единственный приз в 300 долларов. Меняется ли ценность билета как функция от вероятности получения приза? Не считая полезности игры, ценность подобной перспективы может меняться от нуля (когда шансы выигрыша нулевые) до единицы (когда выигрыш 300 долларов гарантирован).
   Интуиция подсказывает, что ценность билета не является линейной функцией от вероятности выигрыша, как следует из правила ожидания. В частности, повышение вероятности от 0 до 5 % явно даст больший эффект, чем повышение с 30 до 35 %, которое, в свою очередь, значит меньше, чем повышение с 95 до 100 %. Эти соображения наводят на мысль об эффекте «границы категорий»: переход от невозможного к возможному или от возможного к достоверному значительнее, чем переход той же величины в середине шкалы. Эта гипотеза отражена в кривой на рисунке 2, показывающей вес, приданный событию, как функцию его заявленной вероятности. Самая заметная особенность рисунка 2 в т ом, что веса решений регрессивны в отношении конкретных вероятностей. Не считая областей, близких к концам графика, увеличение вероятности выигрыша на 0,05 повышает ценность перспективы меньше чем на 5 % от ценности выигрыша. Дальше мы исследуем, какое значение имеет эта психофизическая гипотеза для предпочтений при выборе в ситуации риска.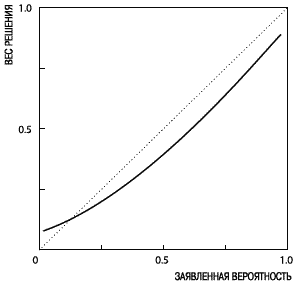

   Рис. 2. Гипотетическая функция веса решения

   На рисунке 2 вес решений ниже соответствующих вероятностей почти на всем промежутке. Недооценка средних и высоких вероятностей по сравнению с гарантированными исходами приводит к неприятию риска в выигрышах, снижая привлекательность позитивных игр. Тот же эффект вызывает стремление к риску в потерях, снижая непривлекательность отрицательных игр. Однако низкие вероятности переоцениваются, а очень низкие вероятности или сильно переоцениваются, или игнорируются полностью, из-за чего в данной области решения весьма нестабильны. Пе реоценка низких вероятностей переворачивает структуру, описанную выше: повышает ценность рискованных попыток и усиливает непривлекательность маленьких шансов на крупную потерю. В результате люди часто рискуют, имея дело с маловероятными выигрышами, и избегают риска, имея дело с маловероятными потерями. Так вес решения влияет на привлекательность лотерей и страховых полисов.
   Нелинейность веса решений неизбежно приводит к нарушению инвариантности, как показано в следующей паре задач.

   Задача 5 (N=85)
   Представьте игру в два этапа. На первом этапе с вероятностью 75 % вы заканчиваете игру, не выиграв ничего, и с вероятностью 25 % переходите на второй этап. На втором этапе вы выбираете вариант.
   А. Гарантированно получить 30 долларов (74 %).
   Б. Выиграть 45 долларов с вероятностью 80 % (26 %).

   Выбор нужно сделать до начала игры, то есть прежде, чем станет и звестен результат первого этапа. Пожалуйста, укажите, какой вариант вы выбираете.

   Задача 6 (N=81)

   Какой из следующих вариантов вы предпочтете?
   В. Выиграть 30 долларов с вероятностью 25 % (42 %).
   Г. Выиграть 45 долларов с вероятностью 20 % (58 %).

   Поскольку существует один шанс из четырех попасть на второй этап в Задаче 5, вариант А предлагает вероятность 0,25 для выигрыша 30 долларов, а вариант Б предлагает вероятность 0,25 0,80 = 0,20 для выигрыша 45 долларов. Таким образом, Задачи 5 и 6 идентичны с точки зрения вероятностей и исходов. Однако предпочтения в двух версиях неодинаковы: явное большинство предпочитает высокие шансы на маленький выигрыш в Задаче 5, но большинство также делает противоположный выбор в Задаче 6. Это нарушение инвариантности подтверждается как для реальных, так и для гипотетических денежных призов (представленные здесь результаты получены в игра х на реальные деньги), а также при выборе количества человеческих жизней и с непоследовательным представлением случайного процесса.
   Мы объясняем нарушение инвариантности взаимодействием двух факторов: формата вероятностей и нелинейности веса решений. Конкретнее, мы предполагаем, что в Задаче 5 люди игнорируют первый этап, исход которого не зависит от принятого решения, и сосредотачиваются на том, что будет, когда они достигнут второго этапа игры. В этом случае, разумеется, человек выбирает между гарантированным выигрышем в случае выбора варианта А и 80 %-ной вероятностью выиграть в случае игры. На самом деле выбор человека в последовательной версии практически идентичен выбору между гарантированным выигрышем 30 долларов и 85 %-ной вероятностью выиграть 45 долларов. Поскольку гарантированный выигрыш переоценивается по сравнению с событиями средней или высокой вероятности, выбор, который может принести гарантированный выигрыш 30 долларов, более привлекателен в после довательной версии. Мы назвали этот феномен «эффектом псевдоопределенности», поскольку исход, в реальности неопределенный, оценивается как определенный.
   Схожий феномен можно продемонстрировать в области низких вероятностей. Представьте, что вы в нерешительности – приобретать или нет страховку на случай землетрясения; взнос довольно высок. Пока вы колеблетесь, дружелюбный страховой агент выдвигает альтернативное предложение: за половину стоимости вы можете получить полную страховку, если землетрясение произойдет в нечетный день месяца. Это выгодно, ведь за половину цены вы страхуете больше половины месяца. Почему большинство сочтет такую вероятностную страховку совсем непривлекательной? Рисунок 2 предлагает ответ. В любом месте области низких вероятностей снижение вероятности с p до p/2 влияет на вес решения значительно меньше, чем снижение вероятности с p/2 до 0. Поэтому снижение риска вдвое не стоит половинного взноса.
   Неприятие вероятностно го страхования важно по трем причинам. Во-первых, оно подрывает классическое объяснение страхования в терминах вогнутой функции полезности. Согласно теории ожидаемой полезности, вероятностное страхование должно быть явно предпочтительней нормального, которое является лишь приемлемым (Kahneman and Tversky 1979). Во-вторых, вероятностное страхование предлагает много защитных действий, таких как диспансеризация, покупка новых шин или установка охранной сигнализации. Эти действия обычно снижают вероятность опасности, не устраняя ее целиком. В-третьих, приемлемость страховки можно обеспечить, установив рамки покрытия непредвиденных обстоятельств. Страховой полис, покрывающий пожар, но не наводнение, например, можно оценивать как полную защиту от одного риска (например, пожара) или как снижение общей вероятности потери собственности. Рисунок 2 позволяет предположить, что люди сильно недооценивают снижение вероятности угрозы по сравнению с полной ликвидацией угрозы. Таким образом, страховка в ыглядит более привлекательной, если формулируется как ликвидация риска, чем если описывается как снижение риска. Словик, Фишхоф и Лихтенштейн (1982) показали, что гипотетическая вакцина, снижающая вероятность заражения болезнью с 20 до 10 %, привлекает меньше, если описана как эффективная в половине случаев, чем если представить ее полностью эффективной против одного из двух различных и равновероятных штаммов вируса, вызывающих сходные синдромы.