Статистика. Данные
 Скачать 0.67 Mb. Скачать 0.67 Mb.
|
|
2. Структурные показатели. Степень асимметрии. Симметричным является распределение, в котором частоты любых двух вариантов, равностоящих в обе стороны от центра распределения, равны между собой. Наиболее точным и распространенным показателем асимметрии является моментный коэффициент асимметрии. As = M3/s3 где M3 - центральный момент третьего порядка. s - среднеквадратическое отклонение. M3 = 1008417642929.4/45 = 22409280953.99 Положительная величина указывает на наличие правосторонней асимметрии Оценка существенности показателя асимметрии дается с помощью средней квадратической ошибки коэффициента асимметрии: 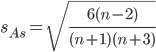 Если выполняется соотношение |As|/sAs < 3, то асимметрия несущественная, ее наличие объясняется влиянием различных случайных обстоятельств. Если имеет место соотношение |As|/sAs > 3, то асимметрия существенная и распределение признака в генеральной совокупности не является симметричным. Расчет центральных моментов проводим в аналитической таблице: Таблица 7- Расчет центральных моментов
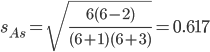 В анализируемом ряду распределения наблюдается несущественная асимметрия (0.422/0.617 = 0.68<3) Применяются также структурные показатели (коэффициенты) асимметрии, характеризующие асимметрию только в центральной части распределения, т.е. основной массы единиц, и независящие от крайних значений признака. Рассчитаем структурный коэффициент асимметрии Пирсона: Для симметричных распределений рассчитывается показатель эксцесса (островершинности). Эксцесс представляет собой выпад вершины эмпирического распределения вверх или вниз от вершины кривой нормального распределения. Чаще всего эксцесс оценивается с помощью показателя: Для распределений более островершинных (вытянутых), чем нормальное, показатель эксцесса положительный (Ex > 0), для более плосковершинных (сплюснутых) - отрицательный (Ex < 0), т.к. для нормального распределения M4/s4 = 3. M4 = 2.2102110044535E+16/45 = 4.9115800098966E+14 Число 3 вычитается из отношения μ4/ σ4 потому, что для нормального закона распределения μ4/ σ4 = 3. Таким образом, для нормального распределения эксцесс равен нулю. Островершинные кривые обладают положительным эксцессом, кривые более плосковершинные - отрицательным эксцессом. Ex < 0 - плосковершинное распределение Чтобы оценить существенность эксцесса рассчитывают статистику Ex/sEx где sEx - средняя квадратическая ошибка коэффициента эксцесса. 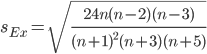 Если отношение Ex/sEx > 3, то отклонение от нормального распределения считается существенным. 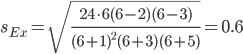 Поскольку sEx < 3, то отклонение от нормального распределения считается не существенным. Показатели вариации. Абсолютные показатели вариации. Размах вариации - разность между максимальным и минимальным значениями признака первичного ряда. R = xmax - xmin = 27600 - 10470 = 17130 руб. Среднее линейное отклонение - вычисляют для того, чтобы учесть различия всех единиц исследуемой совокупности. Каждое значение ряда отличается от другого в среднем на 3129.93 Дисперсия - характеризует меру разброса около ее среднего значения (мера рассеивания, т.е. отклонения от среднего). Несмещенная оценка дисперсии - состоятельная оценка дисперсии (исправленная дисперсия). Среднее квадратическое отклонение. Каждое значение ряда отличается от среднего значения 18559.17 в среднем на 3758.782 Оценка среднеквадратического отклонения. Относительные показатели вариации. К относительным показателям вариации относят: коэффициент осцилляции, линейный коэффициент вариации, относительное линейное отклонение. Коэффициент вариации - мера относительного разброса значений совокупности: показывает, какую долю среднего значения этой величины составляет ее средний разброс. Поскольку v ≤ 30%, то совокупность однородна, а вариация слабая. Полученным результатам можно доверять. Линейный коэффициент вариации или Относительное линейное отклонение - характеризует долю усредненного значения признака абсолютных отклонений от средней величины. Коэффициент осцилляции - отражает относительную колеблемость крайних значений признака вокруг средней. 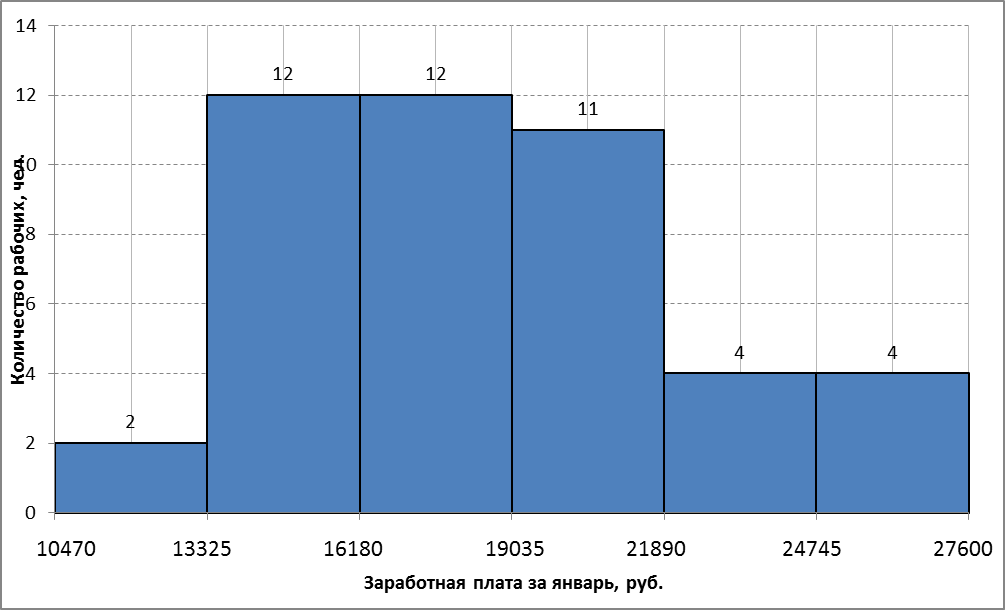 Рисунок 3- Гисторгамма распределения рабочих строительного треста по заработной плате за январь 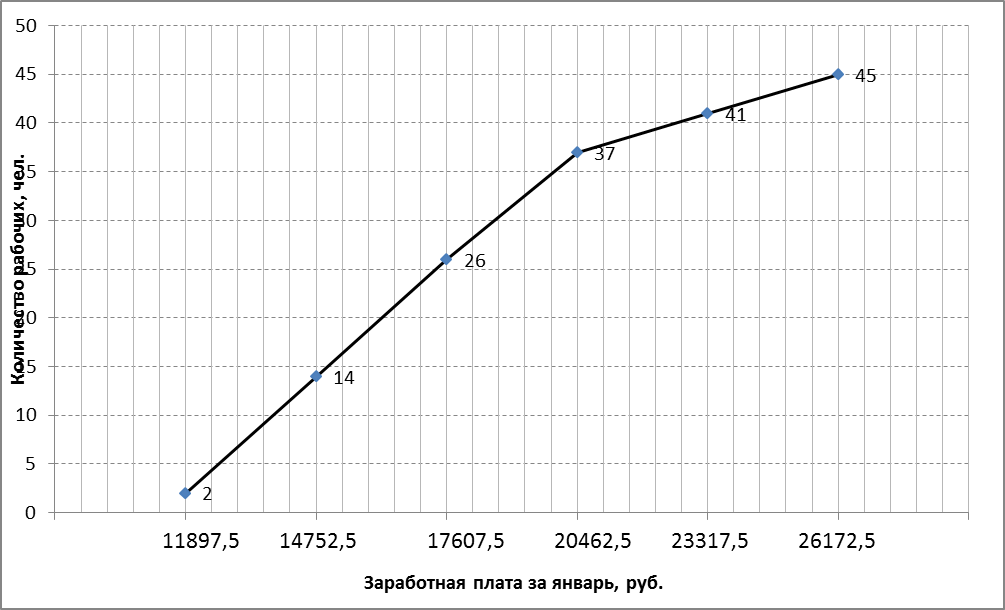 Рисунок 4- Кумулята распределения рабочих строительного треста по заработной плате Ручные расчеты дополним данными, полученными с помощью надстройки «Описательная статистика» пакета Microsoft Excel (Файл – параметры - надстройки – анализ данных – описательная статистика). 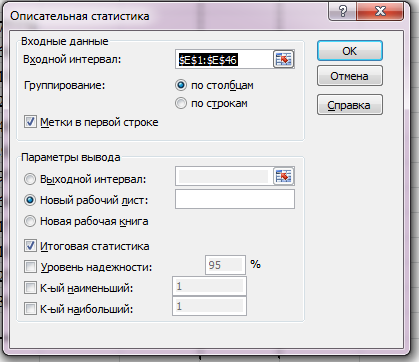 Рисунок 4 - Параметры инструмента Ecxel анализ данных «Описательная статистика» 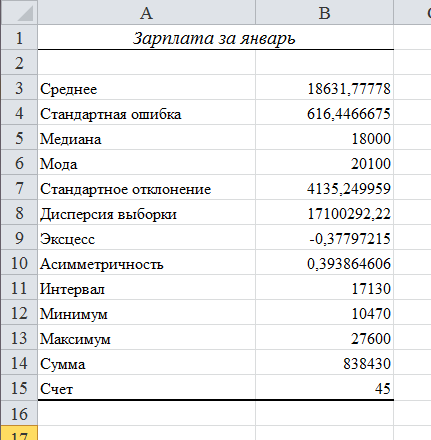 Рисунок 5 - Результаты расчета инструмента Ecxel анализ данных «Описательная статистика» Составим сравнительную таблицу Таблица 4- Сравнительние расчетных параметров
Некоторые параметры отличаются, так как программа рассчитывает не по группированному вариационному ряду данным, а по первичному дискретному ряду. Выводы: Для данного дискретного ряда характерны следующие показатели. Средняя заработная плата за январь составила 18559,17 руб. Наиболее часто встречающееся значение ряда – 16180 руб. 50% единиц совокупности имеют заработную плату меньше по величине 18202.29 руб. В анализируемом ряду распределения наблюдается несущественная правосторонняя асимметрия (0.271/0.612 = 0.44<3). Среднее значение примерно равно моде и медиане, что свидетельствует о нормальном распределении выборки. Значения As и Ex мало отличаются от нуля. Поэтому можно предположить близость данной выборки к нормальному распределению. |
