Контрольная. Расчет вала. Дано t 255 Нм d1 100 мм d2 70 мм l1 50 мм l2 60 мм l 200 мм 100. Рис. Расчётная схема вала. I. Определяем силы, действующие в цилиндрических косозубых передачах

• Название: Дано t 255 Нм d1 100 мм d2 70 мм l1 50 мм l2 60 мм l 200 мм 100. Рис. Расчётная схема вала. I. Определяем силы, действующие в цилиндрических косозубых передачах
• Анкор: Контрольная
• Дата: 24.05.2022
• Размер: 200.79 Kb.
• Имя файла: Расчет вала.docx
• Тип: Документы; #546339

Задание № 14. (схема 6, вариант данных 3).

По заданным геометрическим параметрам вала, крутящему моменту, размеру зубчатых колес выполнить расчет вала на статическую прочность и выносливость. Направление сил, действующих на вал, определяется положением сопряженных зубчатых колес, показанных на рисунке тонкими линиями.

Дано: T = 255 Н·м; d₁ = 100 мм; d₂ = 70 мм; l₁ = 50 мм; l₂ = 60 мм; l = 200 мм;

 = 10⁰.

Рис. 1. Расчётная схема вала.

I). Определяем силы, действующие в цилиндрических косозубых передачах.

В левой цилиндрической косозубой передаче:

F_t1 = = = 5100 Н;

F_r1 = F_t1 = 5100· = 1884,9 Н;

F_a1 = F_t1tan  = 5100·tan 10⁰ = 899,3 Н.

M_a1 = F_a1· = 899,3· = 45 Н·м.
В правой цилиндрической косозубой передаче:

F_t2 = = = 7285,7 Н;

F_r2 = F_t2 = 7285,7· = 2692,7 Н;

F_a2 = F_t2tan  = 7285,7·tan 10⁰ = 1284,7 Н.

M_a2 = F_a2· = 1284,7· = 45 Н·м.
II). Определяем ориентировочные диаметры выходных концов вала из условия прочности при кручении:

 [], откуда W_p = ,

М_{к max} – максимальный крутящий момент (абсолютное значение); [τ] – допускаемое касательное напряжение, принимается в пределах [τ] = 12−40 МПа; W_p – полярный момент сопротивления.

Из эпюры крутящих моментов находим: |М_к|_max = 255 Нм.

Для круглого сечения:

W_p = .

Приняв [τ] = 25 МПа, вычисляем диаметр выходного конца вала:

Минимально допустимый диаметр:

d = = 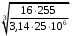= 0,0373 м = 37,3 мм.
Принимаем диаметр вала из ряда нормальных размеров d = 38 мм.

III) Определяем диаметр вала в опасном сечении по третьей теории прочности, т.к. при работе вал испытывает сложную деформацию изгиба с кручением.

Составляем расчетную схему вала со всеми действующими на него силами.

Определяем изгибающие моменты в вертикальной и горизонтальной плоскостях.

а) Составляем расчетную схему от сил, действующих в вертикальной плоскости. Подшипники заменяем шарнирными опорами.



Рис. 2. Эпюра моментов в вертикальной плоскости.
Уравнение моментов сил относительно точки А:

Σ M_A = M_a1 + M_a2 + F_r1 · 0.05 - F_r2 · 0.14 + R_Вв · 0.2= 45 + 45 + 1884,9 · 0.05 - 2692,7 · 0.14 + R_Вв · 0.2 = 0.

Уравнение моментов сил относительно точки B:

Σ M_В = M_a1 + M_a2 + F_r2 · 0.06 - F_r1 · 0.15 + R_Aв · 0.2 = 45 + 45 + 2692.7 · 0.06 - 1884.9 · 0.15 - R_Aв · 0.2 = 0.

Из этих уравнений находим реакции опор.

R_Aв = -156.2 Н. Поскольку реакция получилась с минусом, направляем ее вниз, приняв R_Aв = 156.2Н

R_Вв = 963 Н.

Проверка

ΣY = - R_Aв + R_Вв - F_r2 + F_r1 = - 156.2 + 963 - 2691.7 + 1884.9 = 0

б). Записываем уравнения изгибающих моментов на участках балки , используя метод сечений.

На участке 1-2: (0 ≤ z₁ ≤ 0.05 м )

M(z₁) = - R_Aв · z = - 156.2 · z.

M(0) = 0 Нм;

M(0.05) = -7.808 Нм.

На участке 2-3: (0.05 ≤ z₂ ≤ 0.14 м )

M(z₂) = - R_Aв · z - M_a1 + F_r1·(z - 0.05) = - 156.2 · z - 45 + 1884.9·(z - 0.05)

M(0.05) = -52.808 Нм;

M(0.14) = 102.778 Нм.

На участке 3-4: (0.14 ≤ z₃ ≤ 0.2 м )

M(z₃) = - R_Aв · z - M_a1 - M_a2 - F_r2·(z - 0.14) + F_r1·(z - 0.05) = - 156.2 · z - 45 - 45 - 2691.7·(z - 0.14) + 1884.9·(z - 0.05)

M(0.14) = 57.778 Нм;

M(0.2) = 0 Нм.
в) Составляем расчетную схему от сил, действующих в горизонтальной плоскости. Подшипники заменяем шарнирными опорами.



Рис. 3. Эпюра моментов в горизонтальной плоскости.

Σ M_A = - F_t1 · 0.05 + F_t2 · 0.14 – R_Вг · 0.2= - 5100 · 0.05 + 7286 · 0.14 – R_Вг · 0.2=0

Σ M_В = + F_t1 · 0.15 - F_t2 · 0.06 + R_Aг · 0.2= + 5.1 · 0.15 - 7286 · 0.06 + R_Aг · 0.2=0

Из этих уравнений находим реакции опор.

R_Aг = -1639 Н. Поскольку реакция получилась с минусом, направляем ее вниз, приняв R_Aг = 1639 Н.

R_Вг = 3825 Н.

Проверка

ΣY = - R_Aг + R_Вг + F_t1 - F_t2 = - 1639 + 3825 + 5100 – 7286 = 0

г). Записываем уравнения изгибающих моментов на участках балки , используя метод сечений.

На участке 1-2: (0 ≤ z₁ ≤ 0.05 м ).

M(z₁) = - R_Aг · z = - 1639 · z.

M(0) = 0 кНм;

M(0.05) = -82 Нм.

На участке 2-3: (0.05 ≤ z₂ ≤ 0.14 м ).

M(z₂) = - R_Aг · z + F_t1·(z - 0.05) = - 1639 · z + 5100·(z - 0.05).

M(0.05) = -82 кНм;

M(0.14) = 230 кНм.

На участке 3-4: (0.14 ≤ z₃ ≤ 0.2 м ).

M(z₃) = - R_Aг · z + F_t1·(z - 0.05) - F_t2·(z - 0.14) = - 1639 · z + 5100·(z - 0.05) - 7286·(z - 0.14).

M(0.14) = 230 кНм;

M(0.2) = 0 кНм.
д). Результирующую эпюру изгибающих моментов строим как геометрическую сумму ординат от моментов в вертикальной и горизонтальной плоскостях:

М_рез = .

Находим значение результирующего момента в граничных сечениях:

М_рез1 = = 0 Н;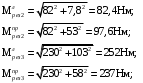



М_рез4 = = 0 Н.



Рис. 4. Эпюра результирующих моментов.
е) Эпюра крутящих моментов.

Участок 1 (0  z₁ l1 м): M_к1 = 0 Нм.

Участок 2 (0  z₂ l3 м): M_к2 = Т = 255 = 255 Нм.

Участок 3 (0  z₃ l2 м): M_к3 = 0 Нм.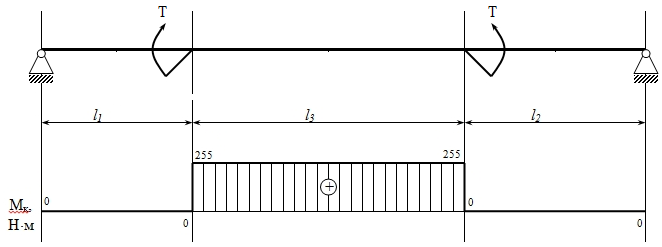



Рис. 5. Эпюра крутящих моментов.
ж). Находим приведенные моменты.

Приведенный момент в характерных точках по третьей теории прочности равен геометрической сумме ординат от результирующих и крутящих моментов. Результирующий момент в месте посадки шестерни и колеса учитываем по максимальному:

М_прив = .
Находим значение приведенного момента в граничных сечениях:
М_прив1 = = 0 Н;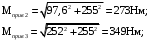



М_прив4 = = 0 Н.



Рис. 6. Эпюра приведенных моментов.
По эпюре приведенного момента устанавливаем опасное сечение.

Видно, что максимальное значение приведенного момента достигается в 3-м сечении и равно:

M_max = 349 Н·м.
з) Подбираем диаметр вала. Материал вала находится в плоском напряженном состоянии от совместного действия изгиба с кручением. Условие прочности записываем в следующем виде:

 [], где W_x = 0,1·d³.
Материал вала при вращении испытывает действие переменных напряжений. Вначале определяем ориентировочный диаметр вала по некоторому условному допускаемому напряжению:

[] = ,

где _в - предел прочности материала;

К - коэффициент запаса прочности, принимаемый равным 8-12.

Данный вал изготавливают из стали 45, для которой _в = 800 МПа:

[] = = 80 МПа.

Таким образом, диаметр вала:

d  = 35,2 мм.

Из ряда нормальных диаметров выбираем ближайший к полученному значению:

d = 36 мм.
IV). Проверку прочности вала при переменных напряжениях производим по тем же нагрузках, по которым был выполнен расчет на статическую прочность. В опасном сечении имеем: М_и = 252 Н·м;

М_кр = 255 Н·м;

d = 36 мм.

1. Вычисляем величину номинальных напряжений.

Нормальные напряжения от изгибающего момента:

 = =

Касательные напряжения от крутящего момента:

 = =
Нормальные напряжения от изгибающего момента при вращении вала меняются по симметричному циклу: _max =  = 54 МПа;

_min = - = -54 МПа;

_m = 0;

_a = _m = 54 МПа;
R =
Касательные напряжения в нереверсивных валах меняются по отнулевому циклу:

_max =  = 27,33 МПа;

_min = 0;

_m = 0,5· = 0,5·27,33 = 13,67 МПа;

_a = 0,5· = 0,5·27,33 = 13,67 МПа;

R = = 0.
2. По таблицам устанавливаем для заданного материала величину пределов выносливости и коэффициентов:

а) Пределы выносливости для стали 45:

_в = 800 МПа:

_-1 = 350 МПа;

_-1 = 210 МПа.

б) Коэффициенты влияния асимметрии циклов:

_ = 0,1;

_ = 0.

в) Коэффициенты концентраций напряжений:

для галтели:

K_ = 2,28;

K_ = 2,37.

для напряженной посадки:

K_ = 2,09;

K_ = 1,71.

для шпонки:

K_ = 2,01;

K_ = 1,88.

Для дальнейшего расчета принимаем:

K_ = 2,28;

K_ = 2,37.

г) Масштабные коэффициенты для d = 36 мм:

K_м = 0,86;

K_м' = 0,8.

д) Коэффициенты состояния поверхности для чистовой обточки:

K_п = K_п' = 0,9.

3) Вычисляем фактический основной коэффициент запаса прочности:
S_ = = = 1,94;

S_ = = = 6,41;

S₀ = = = 1,86.
Коэффициент запаса прочности не выходит за допустимые пределы 1,5 - 3, следовательно, диаметр пересчитывать не надо.

Диаметры остальных сечений вала подбираем конструктивно, после чего чертим вал.



Рис. 7. Эскиз вала.