Задача 4.2 по сопромату. Новосибирский государственный технический университет кафедра прочность летательных аппаратов
 Скачать 42.75 Kb.
|
|
НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ КАФЕДРА «ПРОЧНОСТЬ ЛЕТАТЕЛЬНЫХ АППАРАТОВ» «УТВЕРЖДАЮ» Преподаватель . Фамилия И.О. 2021 г. ЗАДАНИЕ №4.2 «Расчёт допускаемой нагрузки для балки, изготовленной из чугуна» РАЗРАБОТАЛ: Новосибирск 2021 Чугунная балка нагружена в соответствии с заданной расчётной схемой, приведённой на рис. 2, а. При расчёте принять: допускаемое напряжение на растяжение  , допускаемое напряжение на сжатие 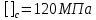 .Исходные данные
  r         r M q   B r       A        2r   F     2    2r  Рис 2. Расчётная схема (а) и поперечное сечение (б) балки Определение реакций опор. Принимаем начало системы координат xy на левом конце балки (рис. 1). Так как направления реакций опор  неизвестны, то предполагаем их направления положительными (направленными вверх). Далее составляем два уравнения равновесия:  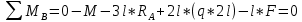  Проверка правильности нахождения реакций опор:  , т.е. реакции определены правильно. Построение эпюр перерезывающих сил  и изгибающих моментов Предварительно разбиваем балку на силовые участки. Границами силовых участков являются точки приложения сосредоточенных нагрузок (сил моментов), начало и конец участка с распределённой нагрузкой. На рис. 1 эти участки обозначены цифрами I, II, III. Рассмотрим последовательно силовые участки, и используя метод сечений, определим внутренние силовые факторы  .Участок I (0 ≤ x ≤ l): M       О  x  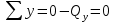   Участок II (l ≤ x ≤ 3l): О x l   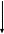 A M q             Участок III (3l ≤ x ≤ 4l):     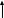О B 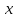 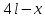        На эпюре  (рис.4) видно, что на участке от l до 3l находится парабола, вычислим координаты вершины параболы. Из подобных треугольников, находим, что координата вершины параболы на оси x будет  ; подставляем это значение х в уравнение моментов на участке l ≤ x ≤ 3l: Геометрические характеристики поперечного сечения: Для определения центра тяжести сложного поперечного сечения, разбиваем сложное сечение на просты фигуры, для которых известно положение их центров тяжести. В данном варианте, выходит две фигуры: прямоугольник без отверстия и квадрат (отверстие), с центрами тяжести  Прямоугольник имеет положительную площадь  а квадрат (отверстие) – отрицательную  , имеем: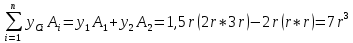  Вычислим координату центра тяжести С сечения (рис.3):  z0 z2 z1 z y2 y 2r 2r r r 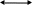С         b1  b2  y1 r    O Рис. 3 Определение центра тяжести С сложного сечения Вычислим моменты инерции составляющих фигур    Вычислим осевой момент инерции сложного поперечного сечения относительно нейтральной оси z.  Рациональное расположение сечения: Наибольший изгибающий момент действует в сечении L и равен  (см. рис. 1). Т.к. значение момента положительно, то нижние волокна сечения растягиваются, а верхние – сжимаются. В этом случае, рациональное сечение показано на рис. 4.Определение допускаемой нагрузки из условия прочности. Определим осевые моменты сопротивления:   Т.к.сечение балки несимметрично относительно оси z, то расчёт на прочность необходимо провести для точки N расположенной в растянутой зоне, и точки А, расположенной в сжатой зоне. Расположим балку рационально (рис.4). Расчёт в растянутой зоне (точка N):   Расчёт в сжатой зоне (точка A): 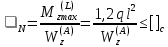  Т.к. изгибающий момент направлен в одном направлении на протяжении всей чугунной балки, то окончательно выбираем значение нагрузки равное:   Эпюра А    —   z С   + N  Рис.4 Рациональное расположение сечения Р  асчётная схема: III F I F  L F  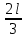 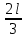  x x F F 2 2 B B A A M M q q    x x  x x                    Рис.1 Расчётная схема балки и эпюры внутренних силовых факторов    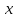II F | ||||||||||||||||||
