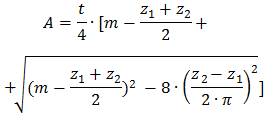|
|
Практическая 2(исправление). Дано z11, t30, c25, d112,d224
Целями практической работы является закрепление теоретического материала и приобретение практических навыков методики расчета и построения профиля зуба звездочки для грузовых пластинчатых цепей.
Дано z=11, t=30, c=25, d1=12,d2=24
Геометрическая характеристика зацепления λ
|
λ = t / Dц
|
INF
|
|
Число зубьев звездочек
|
z ≥ 6
|
11
|
11
|
|
Диаметр делительной окружности dd
|
в шагах dt = cosec(180o/z)
в мм dd = dt ⋅ t
|
3.549
141.96
|
3.549
141.96
|
|
Коэффициент высоты зуба К
|
z
|
Dц≤80
|
Dц>80
|
5-10
|
0,56
|
0,56
|
11-25
|
0,46
|
0,35
|
26-60
|
0,65
|
0,5
|
|
0.46
|
0.46
|
|
Коэффициент числа зубьев
|
Kz = ctg(180 / z)
|
3.41
|
3.41
|
|
Диаметр наружной окружности Dе
|
Dе = t ⋅ (K + Kz - 0.3 / λ)
|
-INF
|
-INF
|
|
Диаметр окружности впадин Di
|
Di = dd - Dc
|
141.96
|
141.96
|
|
Смещение центров дуг впадин е
|
emin = 0,01 ⋅ t
emax = 0,05 ⋅ t
|
emin =0.4
e =1.2
emax = 2
|
|
Радиус впадин r
|
r = 0,5 ⋅ Dц
|
0
|
|
Половина угла заострения зуба γ
|
γ = 13o - 20o
|
17
|
|
Угол впадины зуба β
При изготовлении звездочек методом давления, например, радиальной штамповкой γ = β/z - 180o/z
|
z
|
6-8
|
9-11
|
12-15
|
16-22
|
23-45
|
св. 45
|
β
|
86o
|
68o
|
60o
|
52o
|
48o
|
42o
|
|
|
|
|
Радиус закругления головки зуба, при γ ≤ 2,2
|
r1 =(t - 0,5 ⋅ Dц - 0,5 ⋅ e) ⋅ cos(γ)
|
|
37.678
|
Высота прямолинейного участка профиля зуба при λ ≤ 2,2
|
hr = r1 ⋅ sin(γ )
|
|
11.016
|
Наибольшая хорда для контроля звездочек с нечетным числом зубьев Lx
|
Lx = dd ⋅ cos[90o / z + arcsin(c/dd)] - 2 ⋅ r
|
141.955
|
141.955
|
|
Предельно допустимое увеличение шага цепи по зацеплению со звездочкой
|
Δt ≤ 3%
|
1.2
|
|
Расчет зубьев и венца звездочек в поперечном сечении
|
Ширина зуба звездочки b1
|
для цепей типа 1, 2, 3
bmax = 0,9 ⋅ b3 - 1;
bmin = 0,87 ⋅ b3 - 1,7;
для цепей типа 4
bmax = 0,9 ⋅ (b3 - b2) - 1;
bmin = 0,87 ⋅ (b3 - b2) - 1,7;
|
bmax =12.5
b = 12
bmin = 11.35
|
|
Ширина вершины зуба для цепей
|
типа 1 - b = 0,83 ⋅ b1
типа 2 - b = 0,75 ⋅ b1
типа 3 - b = 0,72 ⋅ b1
типа 4 - b = 0,6 ⋅ b1
|
8.64
|
|
Опорная впадина зуба
|
C = 0,2 ⋅ b1
|
2.4
|
|
Радиус сопряжения зуба со ступицей
|
r2
|
1,6
|
|
Диаметр венца для цепей
|
типа 1 и 2 - Dc = t ⋅ Кz - 1,3 ⋅ h
типа 3 -Dc = t ⋅ Кz - (d4 + 0,25 ⋅ h)
типа 4 -Dc = t ⋅ Кz - (d3 + 0,25 ⋅ h)
|
106.9
|
106.9
|
|
Расчетный угол условного смещения звездочек
|
φс = 3о - 10о
|
5
|
|
Радиус выпуклости
|
Rk = 28,65 ⋅ b3 / φс
|
200.2
|
|
Наименьшее расстояние Аmin при i ≤ 4 можно принимать
|
Аmin = 1,2⋅(De1+De2)/2+(30...50)
|
-INF...-INF
|
|
Межосевое расстояние, создающее благоприятные условия работы А
|
А = (30...50) ⋅ t
|
1200...2000
|
|
Наибольшее расстояние между осями звездочек Аmax
|
А max = 80 ⋅ t
|
3200
|
|
Межосевое расстояние, назначаемое конструктивно
|
a
|
25
|
|
Число звеньев цепи m
|

|
12
|
|
Значение m желательно округлять до ближайшего четного числа (во избежание переходного звена).
|
-
|
12
|
|
Длина цепи Lц
|
Lц = m ⋅ t
|
480
480
|
|
Уточненное расчетное межосевое расстояние A
|
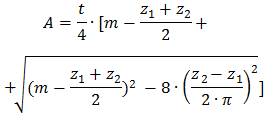
|
20
20
|
| |
|
|
 Скачать 24.38 Kb.
Скачать 24.38 Kb.