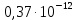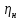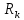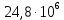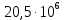Курсовая подземная гидромеханика. Дать сравнительную оценку приближенных методов решения задач теории упругого режима фильтрации нефти
 Скачать 160.08 Kb. Скачать 160.08 Kb.
|
|
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РФ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ «УДМУРТСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ» Институт нефти и газа им. М.С. Гуцериева Кафедра разработки и эксплуатации нефтяных и газовых месторождений им. В.И. Кудинова Курсовая работа по дисциплине: «Подземная гидромеханика» на тему: «Дать сравнительную оценку приближенных методов решения задач теории упругого режима фильтрации нефти» Вариант №19 Выполнил: студент группы 3УсС-21.05.06.01-33 Фазлиахметов Р.А. Проверил: к.н., доцент кафедры РЭНГМ Борхович С.Ю. Ижевск 2022 СОДЕРЖАНИЕ Введение…………………………………………………………………………...3 Теоретическая часть…………………………………………………………..4 Точное решение осесимметричного притока нефти к скважине ………4 Приближенные методы решения задач упругого режима фильтрации нефти………………………………………………………………………..9 Расчетная часть………………………………………………………………13 Рассчитать депрессию на пласт по точной формуле и по приближенным формулам …………………………………….................14 2.2. Найти относительную погрешность расчетов ………………………...15 Выводы…………………………………………………………………………...16 Список использованной литературы…………………………………………...17 ВВЕДЕНИЕ Для уточнения положения, мощности и вертикальной неоднородности коллекторов, определения эффективности перфорации, гидроразрыва, солянокислотной обработки, оценки коэффициента продуктивности отдельных прослоев, а также для решения других задач в разрезе, вскрытом эксплуатационной скважиной, необходимо выделить интервалы, отдающие жидкость, определить дебит из каждого пласта. В нагнетательных скважинах соответственно необходимо выделить интервалы, принимающие жидкость, и определить объем жидкости, поглощаемой, каждым интервалом. Аналогичные исследования необходимо проводить также до и после мероприятий по интенсификации пластов (солянокислотной обработки, гидроразрыва, дополнительной перфорации, и т. п.) с целью выяснения эффективности обработки. В результате исследований получают график изменения суммарного (для всех пластов ниже заданной глубины) или поинтервального дебитов по глубине скважины, называемых профилями притока (поглощения) жидкости или газа. Характерная особенность проявления упругого режима в процессе разработки нефтяных месторождений – длительность процесса перераспределения пластового давления после начала работы скважины или изменения темпа отбора жидкости из скважины. Это связано с тем, что при фильтрации вязкой жидкости в пласте возникают очень большие силы сопротивления. Неустановившиеся процессы протекают тем быстрее, чем больше коэффициент проницаемости пласта, и тем медленнее, чем больше вязкость жидкости и коэффициенты объемной упругости жидкости и пласта ТЕОРЕТИЧЕСКАЯ ЧАСТЬ Точное решение осесимметричного притока нефти к скважине Основы теории движения газа в пористой среде были разработаны основателем советской школы нефтегазовой гидромеханики академиком Л.С. Лейбензоном. Он впервые получил дифференциальные уравнения неустановившейся фильтрации совершенного газа в пласте по закону Дарси. При выводе указанного уравнения предполагалось, что коэффициенты пористости и проницаемости не изменяются с давлением, т.е. пласт недоформируем, вязкость газа также не зависит от давления, газ совершенный. Принимается также, что фильтрация газа в пласте происходит неизменной во времени. Для вывода дифференциального уравнения неустановившейся фильтрации совершенного газа воспользуемся уравнением, которое справедливо для любого сжимаемого флюида: 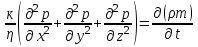 , (1) , (1)где коэффициенты проницаемости и вязкости постоянны. Функция Лейбензона для совершенного газа определяется по формуле: P=ρатp2⁄(2pат) + С. (2) Продифференцируем (2) по координатам 2 раза: 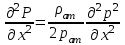 , , 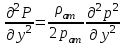 , , 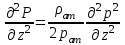 . (3) . (3)Преобразуем правую часть уравнения (1). Считая пористость m0 постоянной и учитывая, что для совершенного газа ρ = ρат p ⁄ pат, (4) получим: 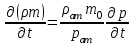 (5) (5)Подставив выражения (3) и (5) в уравнение (1), получим: 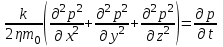 (6) (6)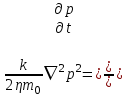 (7) (7)Полученное дифференциальное уравнение неустановившейся фильтрации совершенного газа называется уравнением Лейбензона и представляет собой нелинейное уравнение параболического типа. Подчеркнем, что оно справедливо для совершенного газа при выполнении закона Дарси. Изменением коэффициента пористости пренебрегают потому, что он входит в уравнение в виде произведения ρm, в котором плотность газа меняется в гораздо большей степени, чем пористость Уравнение Лейбензона (6) можно записать по-другому, умножив правую и левую части на давление р и заменив 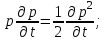 (8) (8)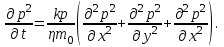 В такой записи под знаками производных по координатам и по времени находится одна и та же функция р2, но коэффициент в правой части kр/(ηm0)-переменный, в него входит искомая функция p(x,y,z,t).. Нетрудно показать, что неустановившаяся фильтрация реального газа с уравнением состояния ρ = ρат p ⁄ [pатz(p)] и с учетом зависимости коэффициента вязкости от давления η=η(p) и недеформируемости пористой среды (m0=const, k=const) описывается следующим нелинейным дифференциальным уравнением параболического типа:  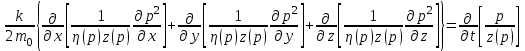 (9) (9)Для решения конкретных задач, связанных с неустановившейся фильтрацией газа, дифференциальное уравнение в форме (6) или (8) должно быть проинтегрировано по всей области газовой залежи при заданных начальных и граничных условиях. Так как уравнение (6) или (8) представляет собой сложное нелинейное уравнение в частных производных, оно в большинстве случаев не имеет точных аналитических решений. Его можно проинтегрировать численно с помощью ЭВМ или решить приближенным способом. Приближенные способы хорошо разработаны. Численные методы решения различных задач фильтрации газа на основе уравнения Л.С. Лейбензона также достаточно хорошо обоснованы в приложениях к проблемам разработки месторождений природных газов. При этом наибольшее распространение получили методы конечных разностей и конечных элементов. Вместе с тем. развитие теории фильтрации газов, вызванное требованиями практики разработки газовых месторождений, и. в частности, изменением горно-геологических условий их залегания (большие глубины, высокие давления и температуры, многокомпонентность газа и т.д.) потребовало учета в основном уравнении, предложенном Л.С. Лейбензоном, многих дополнительных факторов. Так. оказалось, что использование функции Лейбензона в форме (2) допустимо при небольших давлениях, в условиях недеформируемых пластов. При достаточно больших давлениях в условиях деформируемых коллекторов под знак интеграла в формуле (2) необходимо внести зависимости изменения проницаемости, вязкости и коэффициента сверхсжимаемости газа от давления. При неизотермической фильтрации во многих случаях необходимо учитывать также изменение свойств газа oт температуры. Уравнение (6) получено с использованием в качестве уравнения движения закона Дарси. Вместе с тем, последующие исследования И.А.Чарного, Е.М. Минского и других показали, что при фильтрации газов в природных пластах в большинстве случаев следует пользоваться нелинейным (двучленным)законом фильтрации. Математические трудности в решении получающегося при этом дифференциального уравнения. Отметим, что одним из эффективных путей решения уравнения Лейбензона является линеаризация, т.е. сведение его к линейному уравнению Фурье. Как покажем при дальнейшем рассмотрении, в некоторых практических случаях использование различных способов линеаризации уравнения (6) позволяет получать приближенные решения, удовлетворяющие требованиям практики. Будем считать пласт недеформируемым, фильтрацию изотермической и происходящей по двучленному закону. Рассмотрим плоскорадиальный поток к осесимметрично расположенной скважине. Воспользуемся уравнением неразрывности для плоскорадиального движения: 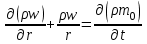 (10) (10)Воспользовавшись выражением для массовой скорости ρw, полученным из двучленного закона фильтрации, после подстановки в них значений плотности из уравнения состояния (4), получим:  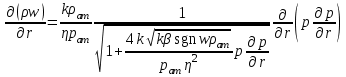 ; (11) ; (11)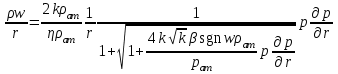 . (12) . (12)Подставив выражения (11), (12) и (5) в уравнение неразрывности (10) и сократив на ρат / pат , получим: 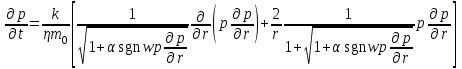 ,(13) ,(13)где 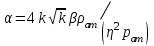 . .Если сделать замену 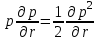 , то дифференциальное уравнение неустановившейся фильтрации газа по двучленному закону примет следующий вид: , то дифференциальное уравнение неустановившейся фильтрации газа по двучленному закону примет следующий вид: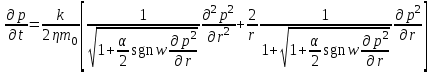 . (14) . (14)Аналитическое решение уравнения (14) наталкивается на значительные трудности, однако численное решение для обычных в подземной гидромеханике начальных и граничных условий не представляет затруднений. 1.2 Приближенные методы решения задач упругого режима фильтрации нефти Решение задачи о притоке нефти к скважине методом последовательной смены стационарных состояний. Этот метод основан на следующих предпосылках: в каждый момент времени существует конечная возмущенная область, в которой происходит движение газа к скважине; движение внутри возмущенной области стационарно; размер возмущенной области определяется из условия материального баланса. Решим этим методом ту же задачу о неустановившемся притоке газа к скважине с постоянным заданным дебитом Qат, но будем считать радиус скважины конечным и равным rc. В любой момент времени возмущенной областью является круговая область радиусом R(t), внутри которой давление распределено по стационарному закону 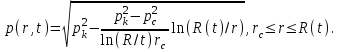 Вне возмущенной области давление равно начальному (невозмущенное состояние): р=рk,r>R(t) В возмущенной области можно написать также выражение для дебита для стационарной фильтрации: 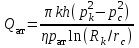 Заметим, что в рассматриваемой задаче забойное давление является функцией времени. Найдем из формулы отношение 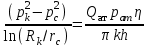 и подставим его в формулу для давления в возмущенной области. В результате получим: 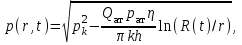 т. е. распределение давления, выраженное через заданный дебит и параметры пласта. Для нахождения R(t) составим уравнение материального баланса. Начальный запас газа (при р=рk) в зоне пласта радиусом R(t): 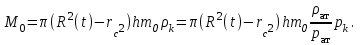 Текущий запас газа выразим через средневзвешенное давление 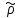 : :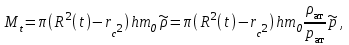 где 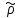 определяется по формуле установившейся фильтрации определяется по формуле установившейся фильтрации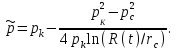 Так как отбор газа происходит с постоянным дебитом Qат, то отобранная масса газа к моменту t равна ρатQатt. Таким образом, М0-мt= ρатQатt 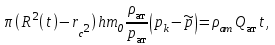 Подставив в последнее соотношение выражение для средневзвешенного давления 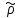 и для Qат, получим: и для Qат, получим: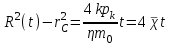 или 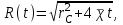 Для значений времени, для которых 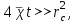 имеем: имеем: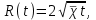 Теперь, зная закон движения границы возмущенной области в виде, можно найти давление в любой точке пласта в любой момент времени по формуле, а также изменение давления на забое скважины в любой момент времени 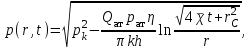 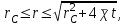 р=рк, р=рк, 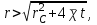 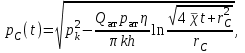 Метод усреднения Еще одним приближенным методом, применительно к задачам неустановившейся фильтрации нефти, является метод усреднения временной производной по пространству. В качестве примера рассматривается прямолинейно-параллельная фильтрация нефти. Соответствующее этому случаю точное дифференциальное уравнение имеет вид 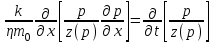 (12) (12)Допущением является то, что коэффициент сверхсжимаемости z(р) можно заменить на 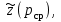 где pср - некоторое среднее давление в области фильтрации. Введем обозначение р1=р/z(р). Тогда уравнение примет вид где pср - некоторое среднее давление в области фильтрации. Введем обозначение р1=р/z(р). Тогда уравнение примет вид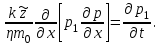 (13) (13)Пусть имеется первоначально невозмущенный газонасыщенный пласт шириной В, толщиной h, длиной L. С трех сторон пласт ограничен непроницаемыми поверхностями, а с четвертой стороны (х = 0) вскрыт галереей. В момент t = 0 через галерею начинает отбираться нефть с постоянным массовым дебитом, который в соответствии с законом Дарси можно записать в виде: 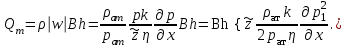 Требуется определить давление в пласте в любой момент времени t > 0. Для этого нужно найти решение уравнения (13) в области изменения 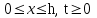 удовлетворяющее начальному и граничным условиям: удовлетворяющее начальному и граничным условиям:p1 = p10 при t = 0 (40) 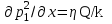 при x=0, где при x=0, где 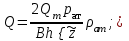 (14) (14)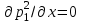 при x = L (15) при x = L (15)Как и в методе последовательной смены стационарных состояний принимаем, что в каждый момент времени существует конечная возмущенная область l(t), на границе которой выполняются условия p12=p102, 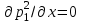 при x = l(t) (16) при x = l(t) (16)Центральным моментом в рассматриваемом методе усреднения является принятие условия 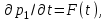 РАСЧЕТНАЯ ЧАСТЬ
2.1 Рассчитать депрессию на пласт по точной формуле и по приближенным формулам 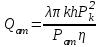 Подставив наши данные, получим: 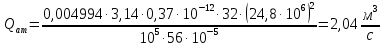 определим коэффициент 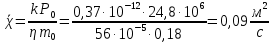 Точное решение Определим безразмерную величину ξ для r = rc 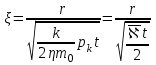 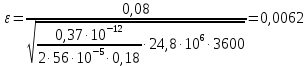 Сравнивая полученное значение ξ со значениями в таблице 1 для λ=0,004994 заключаем, что ξ < ξ* поэтому безразмерное давление F определим по формуле 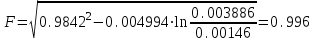 . .Выразив давление P = Pc, получим Pc= FPk = ּ 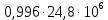 = 24,7ּ Па = 24,7ּ ПаДепрессия на пласт через 1 час будет равна: ∆P = Pk-Pc = (24,8-24,7)ּ106 = 0,1 МПа. Расчет методом последовательной смены стационарных состояний 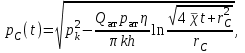 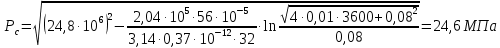 Депрессия будет равна: ∆ P = (24,8-24,6)ּ106 = 0,2 МПа. 2.2 Относительная погрешность расчетов 1. Расчет по линеаризованной формуле: 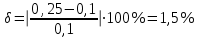 2. Расчет методом последовательной смены стационарных состояний: 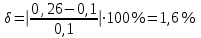 ВЫВОД Линеаризованная формула эффективна только в тех случаях, когда радиус скважины очень маленький, потому что в этом случае воронка депрессии очень крутая и давление по всему пласту в целом не сильно отличается от начального. Но при больших радиусах скважины эта формула будет давать большую погрешность, т.к. давление по пласту будет сильно отличаться от начального. В отличие от линеаризованной формулы, формула последовательной смены стационарных состояний эффективна для любых радиусов скважин, но только для первой фазы движения, т.е. пока воронка депрессии не достигнет радиуса контура. Как показали расчеты наиболее точной является линеаризованная формула. СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ Басниев К.С., Дмитриев Н.М., Розенберг Г.Д. Нефтегазовая гидромеханика: Учебник для вузов. - Москва-Ижевск: Институт компьютерных исследований, 2003. - 480 с. Басниев К.С. и др. Подземная гидромеханика. М.: Недра, 1993 г., 172-179 с. Басниев К.С. и др. Подземная гидромеханика. М.:Недра, 1993 г., 131-151 с., 159-171 с. Басниев К.С., Дмитриев Н.М., Розенберг Г.Д. Нефтегазовая гидромеханика: Учебное пособие для вузов. - М. - Ижевск: Институт компьютерных исследований, 2005, 544 с. Подземная гидромеханика: Учебно-методическое пособие / сост. С.Ю. Борхович, И.В. Пчельников, С.Б. Колесова – Ижевск: Издательский центр «Удмуртский государственный университет» 2017 |

 103
103