Изотермическое расширение

• Название: Изотермическое расширение
• Дата: 27.10.2021
• Размер: 38.89 Kb.
• Имя файла: 30,31,32,39.docx
• Тип: Документы; #257365

30.Цикл Карно. КПД цикла. Холодильный коэффициент
Цикл Карно состоит из четырёх обратимых стадий, две из которых осуществляются при постоянной температуре (изотермически), а две — при постоянной энтропии (адиабатически).

1. Изотермическое расширение . В начале процесса рабочее тело имеет температуру  {\displaystyle T_{H}}, то есть температуру нагревателя. При расширении рабочего тела его температура не падает за счет передачи от нагревателя количества теплоты  {\displaystyle Q_{H}}, то есть расширение происходит изотермически (при постоянной температуре) . При этом объём рабочего тела увеличивается, оно совершает механическую работу, а его энтропия возрастает.

2. Адиабатическое расширение. Рабочее тело отсоединяется от нагревателя и продолжает расширяться без теплообмена с окружающей средой. При этом температура тела уменьшается до температуры холодильника  {\displaystyle T_{X}}, тело совершает механическую работу, а энтропия остаётся постоянной.

3. Изотермическое сжатие. Рабочее тело, имеющее температуру  {\displaystyle T_{X}}, приводится в контакт с холодильником и начинает изотермически сжиматься под действием внешней силы, отдавая холодильнику количество теплоты  {\displaystyle Q_{X}}. Над телом совершается работа, его энтропия уменьшается.

4. Адиабатическое сжатие . Рабочее тело отсоединяется от холодильника и сжимается под действием внешней силы без теплообмена с окружающей средой. При этом его температура увеличивается до температуры нагревателя, над телом совершается работа, его энтропия остаётся постоянной.


В термодинамике цикл Карно́ или процесс Карно́ — это идеальный круговой процесс, состоящий из двух адиабатных и двух изотермических процессов
В процессе Карно термодинамическая система выполняет механическую работу за счёт обмена теплотой с двумя тепловыми резервуарами, имеющими постоянные, но различающиеся температуры. Резервуар с более высокой температурой называется нагревателем, а с более низкой температурой — холодильником
Холодильный коэффициент, безразмерная величина (обычно больше единицы), характеризующая энергетическую эффективность работы холодильной машины; равна отношению холодопроизводительности к количеству энергии (работе), затраченной в единицу времени на осуществление холодильного цикла.

31.Второе начало термодинамики. Неравенство Клаузиуса
Второе начало термодинамики в формулировке Клаузиуса утверждает, что процесс, при к-ром не происходит никаких изменений, кроме передачи тепла от горячего тела к холодному, необратим, т. е. теплота не может самопроизвольно переходить от более холодного тела к более горячему (принцип Клаузиуса).

Неравенство Клаузиуса: Количество теплоты, полученное системой при любом круговом процессе, делённое на абсолютную температуру, при которой оно было получено, неположительно.
Рассматривая циклич. процесс, при к-ром система получает (или от неё отнимают) малые кол-ва теплоты dQ при абс. температуре T, можно сформулировать второе начало термодинамики в виде Клаузиуса неравенства

1. 
    Неравенство Клаузиуса можно записать в след. виде:   (знак равенства соответствует обратимым процессам). Это неравенство - другая, интегральная формулировка второго начала термодинамики. Из него следует, что для адиабатически изолиров. системы  при необратимых процессах энтропия возрастает, а при обратимых - остаётся неизменной.
   
   32. Энтропия и ее свойства.
   

Энтропия —физическая величина, используемая для описания термодинамической системы, одна из основных термодинамических величин энтропия и температура — сопряжённые термодинамические величины, необходимые для описания термических свойств системы и тепловых процессов в ней

Качественные представления о термическом состоянии системы связаны с тепловыми ощущениями, выражаемыми понятиями «теплее», «холоднее», «нагрев», «охлаждение», «степень нагретости». К термическим относят свойства, характеризующие поведение вещества при его нагреве или охлаждении: термические коэффициенты, теплоёмкость и другие калорические коэффициенты, постоянную Кюри, показатели термостойкости, пределы огнестойкости и т. Д
Перечисление свойств энтропии дано применительно к термодинамике Гиббса; примеры, приводимые для иллюстрации перечисляемых свойств энтропии, относятся, как правило, к открытым однородным термодеформационным системам, для которых справедливо фундаментальное уравнение Гиббса в энтропийном выражении Энтропия в фундаментальном уравнении в энтропийном выражении есть характеристическая функция, то есть фундаментальное уравнение содержит все термодинамические сведения о данной системе

39. Уравнение Клайперона-Клаузиуса. Фазовые переходы II рода.
 термодинамическое уравнение, относящееся к квазистатическим (равновесным) процессам перехода вещества из одной фазы в другую (испарение, плавление, сублимация, полиморфное превращение и др.). Согласно уравнению, теплота фазового перехода (например, теплота испарения, теплота плавления) при квазистатическом процессе определяется выражением 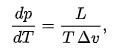Координатная плоскость T–P с нанесенными на нее кривыми фазового равновесия называется диаграммой состояния. Кривые фазового равновесия делят координатную плоскость на области, которым соответствуют различные фазовые состояния вещества, например: твердое, жидкое и газообразное
Фазовые переходы второго рода — фазовые переходы, при которых вторые производные термодинамических потенциалов по давлению и температуре изменяются скачкообразно, тогда как их первые производные изменяются постепенно. Фазовые переходы второго рода происходят в тех случаях, когда меняется симметрия строения вещества (симметрия может полностью исчезнуть или понизиться).
Фазовые переходы второго рода сопровождаются изменением симметрии вещества. Изменение симметрии может быть связано со смещением атомов определённого типа в кристаллической решётке, либо с изменением упорядоченности вещества.

В большинстве случаев, фаза, обладающая большей симметрией (то есть включающей в себя все симметрии другой фазы), соответствует более высоким температурам, но существуют и исключения. Например, при переходе через нижнюю точку Кюри в сегнетовой соли, фаза, соответствующая меньшей температуре, обладает ромбической симметрией, в то время как фаза, соответствующая большей температуре, обладает моноклинной симметрией.

Для количественной характеристики симметрии при фазовом переходе второго рода вводится параметр порядка, принимающий отличные от нуля значения в фазе с меньшей симметрией, и тождественно равный нулю в неупорядоченной фазе.

{\displaystyle {\frac {dp}{dT}}={\frac {L}{T\,\Delta v}},}