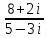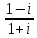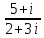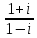пр р. Действия над действительными числами
 Скачать 38.01 Kb.
|
|
Практическое занятие № 1 Тема: «Действия над действительными числами» Цели: формировать умение графического изображения комплексных чисел, выполнения арифметических операций с действительными числами. Оборудование: тетрадь для практических работ, ручка, простой карандаш, линейка, методические рекомендации по выполнению работы. Указание. Практическая работа состоит из двух частей – теоретической и практической. После изучения теоретического материала можно приступать к выполнению практической части. Она состоит из одной или более задач для самостоятельного выполнения и контрольных вопросов. Не забывайте о правильном оформлении решения. Каждое правильно выполненное задание оценивается определенным количеством баллов. Порядок выполнения работы Рассмотрите теоретический материал по теме и примеры решения задач (приведены ниже). Решите самостоятельную работу. Оформите решение письменно в тетради. Ответьте письменно на контрольные вопросы. Ход работы Актуализация опорных знаний Перечислите множества чисел. Какое множество включает все числа? При округлении, когда мы прибавляем «1» к предыдущему числу, когда отбрасываем числа? При преобразовании бесконечной периодической дроби на что надо обратить внимание? Теоретическая часть Изучение математики начинается с натуральных чисел, т.е. с чисел 1, 2, 3, 4, 5,… . При сложении и умножении натуральных чисел всегда получаются натуральные числа. Однако разность и частное натуральных чисел могут не быть натуральными числами. Дополнением натуральных чисел нулем и отрицательными числами (т.е. числами, противоположными натуральным) множество натуральных чисел расширяется до множества целых чисел, т.е. чисел 0, ± 1, ± 2, ± 3, … . При сложении, вычитании и умножении целых чисел всегда получаются целые числа. Однако частное двух целых чисел может не быть целым числом. При выполнении четырех арифметических действий (кроме деления на нуль) над рациональными числами всегда получаются рациональные числа. Бесконечную десятичную дробь 0,3333… называют периодической, повторяющуюся цифру 3 – ее периодом. Периодическую дробь 0,333… коротко записывают так: 0,(3); читается: «Ноль целых и три в периоде». Периодическая дробь – это бесконечная десятичная дробь, у которой начиная с некоторого десятичного знака повторяется одна и та же цифра или несколько цифр – период дроби. Если бесконечная десятичная дробь непериодическая, то она не является рациональным числом. Например, дробь 0,101001000100001…, в которой после первой цифры 1 стоит один нуль, после второй цифры 1 – два нуля и, вообще, после n – й цифры стоит nнулей, не является периодической. Поэтому написанная дробь не представляет никакого рационального числа. В этом случае говорят, что данная дробь является иррациональным числом. Иррациональным числом называется бесконечная десятичная непериодическая дробь. Изображение комплексных чисел. Комплексные числа записываются в виде: a+ bi. Здесь a и b – действительные числа, а i – мнимая единица, т.e. i 2 = –1. Число a называется абсциссой, a b – ординатой комплексного числа a+ bi. Комплексное число 0+ bi называется чисто мнимым числом. Запись bi означает то же самое, что и 0+ bi. Модулем комплексного числа называется длина вектора OP, изображающего комплексное число на координатной (комплексной) плоскости. Сопряжённые комплексные числа имеют одинаковый модуль Рассмотрим на плоскости декартову прямоугольную систему координат xOy . Каждому комплексному числу z = a + bi можно сопоставить точку с координатами (a;b) , и наоборот, каждой точке с координатами (c;d) можно сопоставить комплексное число w = c + di . Таким образом, между точками плоскости и множеством комплексных чисел устанавливается взаимно однозначное соответствие. Поэтому комплексные числа можно изображать как точки плоскости. Плоскость, на которой изображают комплексные числа, обычно называют комплексной плоскостью. Пример. Изобразим на комплексной плоскости числа Z1 = 2 + i; z2 = 3i; z3 = -3 + 2i; z4 = -1 – i. Решение:   а в А 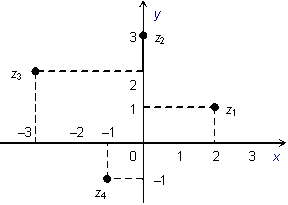 рифметические действия над комплексными числами те же, что и над действительными: их можно складывать, вычитать, умножать и делить друг на друга. Сложение и вычитание происходят по правилу (a + bi) ± (c + di) = (a ± c) + (b ± d)i, а умножение — по правилу (a + bi) · (c + di) = (ac – bd) + (ad + bc)i (здесь как раз используется, что i2 = –1). Число  = a – bi называется комплексно-сопряженным к z = a + bi. Равенство z · = a2 + b2 позволяет понять, как делить одно комплексное число на другое (ненулевое) комплексное число: .Например,  Практическая часть Часть 1 (фронтальная работа) З 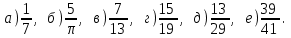 адание 1. Представить в виде бесконечной десятичной дроби числа. Выполнить деление столбиком, не используя калькулятор.Задание 2. Преобразовать бесконечную периодическую дробь в обыкновенную: 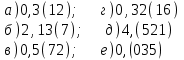 Часть 2 (самостоятельная работа)
Вывод: (запишите вывод о проделанной работе) Критерии оценки
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
