Название: пр.раб.№5. КОМПЛЕКСНЫЕ ЧИСЛА (1). Комплексные числа определение
 Скачать 301.4 Kb. Скачать 301.4 Kb.
|
|
КОМПЛЕКСНЫЕ ЧИСЛА. алгебраическая, ТРГОНОМЕТРИЧЕСКАЯ И ПОКАЗАТЕЛЬНАЯ ФОРМУЛА КОМПЛЕКСНОГО ЧИСЛА, ДЕЙСТВИЯ С КОМПЛЕКСНЫМИ ЧИСЛАМИ, ИРРАЦИОНАЛЬНЫЕ КОМПЛЕКСНЫЕ ЧИСЛА. Манухина м в . Пкш-21. Комплексные числа определение. Комплексное число — это выражение вида a + bi, где a, b — действительные числа, а i — так называемая мнимая единица, символ, квадрат которого равен –1, то есть i2 = –1. Число a называется действительной частью, а число b — мнимой частью комплексного числа z = a + bi. Если b = 0, то вместо a + 0i пишут просто a. Видно, что действительные числа — это частный случай комплексных чисел. Арифметические действия над комплексными числами те же, что и над действительными: их можно складывать, вычитать, умножать и делить друг на друга. Сложение и вычитание происходят по правилу (a + bi) ± (c + di) = (a ± c) + (b ± d)i, а умножение — по правилу (a + bi) · (c + di) = (ac – bd) + (ad + bc)i (здесь как раз используется, что i2 = –1). Число  = a – bi называется комплексно-сопряженным к z = a + bi. Равенство z · = a – bi называется комплексно-сопряженным к z = a + bi. Равенство z ·  = a2 + b2 позволяет понять, как делить одно комплексное число на другое (ненулевое) комплексное число: = a2 + b2 позволяет понять, как делить одно комплексное число на другое (ненулевое) комплексное число: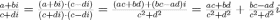 . .История комплексных чисел. Исторически комплексные числа впервые были введены в связи с выведением формулы вычисления корней кубического уравнения в первой половине 16 века получил выражение для корня такого уравнения через некоторые параметры, для нахождения которых составляется система. Но было выяснено, что такая система не для всех кубических уравнений имела решение в действительных числах. Это непонятное на то время явление объяснил в 1572 году Рафаэль Бомбелли (1526 - 1572), что по сути было введением комплексных чисел и действий над ними. Но долгое время полученные результаты многими учеными считались сомнительными и лишь в 19 веке после появления трудов немецкого математика, механика, физика, астронома и геодезиста Карла Фридриха Гаусса (1777 - 1855) существование комплексных чисел стало общепризнанным. Символ В современной математике комплексное число является одним из фундаментальнейших понятий, находящее применение и в «чистой науке», и в прикладных областях. Понятно, что так было далеко не всегда. В далекие времена, когда даже обычные отрицательные числа казались странным и сомнительным нововведением, необходимость расширения на них операции извлечения квадратного корня была вовсе неочевидной. Тем не менее, в середине XVI века математик Рафаэль Бомбелли вводит комплексные (в данном случае точнее сказать, мнимые) числа в оборот. Собственно, предлагаю посмотреть, в чем была суть затруднений, доведших в итоге солидного итальянца до подобных крайностей. Сам термин «комплексное число» впервые ввел в научный обиход Л.Карно, но ис-пользовать его стали только после того, как в работах К.Гаусса и У. Гамильтона была по-строена арифметическая теория комплексных чисел и дана их геометрическая интерпрета-ция. Комплексные числа. Алгебраическая форма комплексного числа.Определение. Числа вида 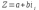 (где (где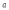 –действительная часть; –действительная часть;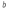 –мнимая часть; –мнимая часть; 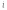 – мнимая единица), называются комплексными. – мнимая единица), называются комплексными.Запись 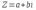 называется алгебраической формой комплексного числа. называется алгебраической формой комплексного числа.Комплексное число a+bi считается равным нулю, если его действительная и мнимая части равна нулю: a=b=0 Комплексное число а+bi при b=0 считается совпадающим с действительным числом а; a+0i=a =bi. Два комплексных числа z=a+bi и z=a-bi, отличающиеся лишь знаком мнимой части, называются сопряженными. Геометрическое изображение Ось OX – действительная ось Ось OY – мнимая ось Комплексная плоскость 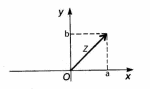 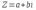 RealZ = a– действительная часть ImaginaryZ = b– мнимая часть Действия над комплексными числами в алгебраической форме..1) Сумма (разность) комплексных чисел 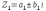 ; ; 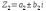 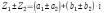 2) Произведение комплексных чисел 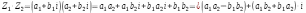 (учли, что 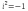 ) )3) Деление комплексных чисел Для того чтобы выполнить деление комплексных чисел, надо числитель и знаменатель умножить на комплексное число, сопряженное знаменателю: 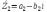 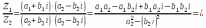 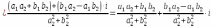 Следовательно, 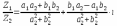 Тригонометрическая формулы.Любое комплексное число (кроме нуля) z=a+bi можно записать в тригонометрической форме: z=|z|∙ (cosφ+isinφ), где |z| – это модуль комплексного числа, а φ – аргумент комплексного числа. Модулем комплексного числа называется расстояние от начала координат до соответствующей точки комплексной плоскости. Попросту говоря, модуль – это длина радиус-вектора . По теореме Пифагора легко вывести формулу для нахождения модуля комплексного числа: 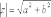 . Данная формула справедлива для любых значений «а» и «бэ». . Данная формула справедлива для любых значений «а» и «бэ». Аргументом комплексного числа называется угол между положительной полуосьюдействительной оси и радиус-вектором, проведенным из начала координат к соответствующей точке. Аргумент не определён для единственного числа: 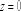 . . Из геометрических соображений получается следующая формула для нахождения аргумента: 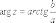 Запомним , модуль – длина (которая всегда неотрицательна), аргумент – угол. Представим в тригонометрической форме число . Найдем его модуль и аргумент. Очевидно, что 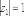 . Формальный расчет по формуле: . Формальный расчет по формуле: 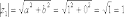 . Очевидно, что . Очевидно, что 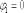 (число лежит непосредственно на действительной положительной полуоси). Таким образом, число в тригонометрической форме: (число лежит непосредственно на действительной положительной полуоси). Таким образом, число в тригонометрической форме: 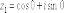 обратное проверочное действие: 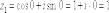  Показательная формула комплексного числа z = |z| • е iф Любое комплексное число (за исключением 0) можно представить в показательной форме: z = |z| • е iф, где |z| — модуль, ф — аргумент комплексного числа. Представим комплексное число в тригонометрической форме: z = |z| • (соs ф + isin ф), где согласно формулы Эйлера: соs ф + isin ф = е iф, отсюда, получим комплексное число в показательной форме: z = |z| • е iф. Формула Эйлера. Показательная форма комплексного числаПолагая в формуле (10.1) х=0, получим. Это равенство носит название формулы Эйлера (Эйлер – немецкий математик, академик Российской Академии наук). Пользуясь формулой Эйлера, можно представить комплексное число z в виде. Итак, - показательная форма Помимо алгебраической и тригонометрической имеется еще показательная форма записи комплексного числа, которая широко используется в различных приложениях, в частности в электротехнике. Пусть 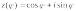 , зависит от действительной переменной φ. , зависит от действительной переменной φ.Сопоставим взаимно однозначным образом каждому комплексному числу комплексно показательное выражение 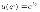 . С помощью операций дифференцирования можно показать, что эти выражения имеют одну и ту же логическую сущность, в связи с этим полагают по определению . С помощью операций дифференцирования можно показать, что эти выражения имеют одну и ту же логическую сущность, в связи с этим полагают по определениюЭта формула называется формулой Эйлера и представляет собой определение комплексной показательной функции 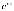 , где φ – любое действительное число. , где φ – любое действительное число.Пусть дано комплексное число z =r (cosφ + isinφ). Сопоставляя это с предыдущей формулой, получаем 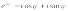 . Эта формула называется формулой Эйлера и представляет собой определение комплексной показательной функции . Эта формула называется формулой Эйлера и представляет собой определение комплексной показательной функции 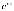 , где φ – любое действительное число. , где φ – любое действительное число. 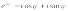 Пусть дано комплексное число z =r (cosφ + isinφ). Сопоставляя это с предыдущей формулой, получаем 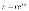 . .Такая форма записи комплексного числа называется показательной формой комплексного числа.  Действия с комплексными числами. Над комплексными числами в алгебраической форме можно выполнить следующие действия : Сложение. Определитель. Суммой комплексных чисел z1=a1+b1i и z2=a2+b2i называется комплексное число z действительная часть которого равна сумме действий частей z1 и z2 , и мнимая часть – сумме мнимых частей чисел z1 и z2, то есть z=(a1 +a2)+(b1+b2)i. Числа z1 и z2 называют слагаемыми. Вычитание. Вычесть из комплексного числа z1 комплексное число z2 значит найти комплексное число z, что z+z2=z1 . Умножение . произведение комплексных чисел z1=ai+b1i и z2=a2+b2i . называется комплексное число z, определяемое равенством: z=(a1a2-b1b2) +(a1a2+b1b2). Число z1 и Z2 называют сомножителем. Диление.  иррациональные комплексные числа Иррациональное число. Иррациона́льное число́ — это вещественное число, которое не является рациональным, то есть не может быть представлено в виде обыкновенной дроби {\displaystyle {\frac {m} {n}}}, где m, n {\displaystyle m, n} — целые числа, n ≠ 0 {\displaystyle n\neq 0}. Иррациональное число может быть представлено в виде бесконечной непериодической десятичной дроби |
