311. Тонкий стержень длиной L = 20 см несет равномерно распределенный заряд Q=0,1мкКл. Определить напряженность Е электрического поля, создаваемого распределенным зарядом в точке А, лежащей на оси стержня на расстоянии а = 20 см от его конца.
a = 20 см
Q=0.1 мкКл
L = 20 см
|

Определим напряженность dE, созданную элементарным зарядом dq=ρ×dr на расстоянии r (см. рис.) 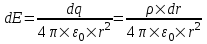 , где , где 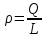 – линейная плотность зарядов стержня. Тогда полная напряженность равна интегралу – линейная плотность зарядов стержня. Тогда полная напряженность равна интегралу 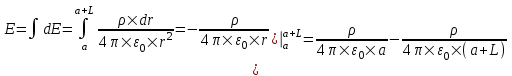 . .
Так как 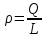 , то , то 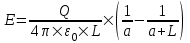 . .
Подставляем числа (переводя одновременно все величины в систему СИ). 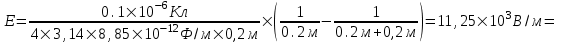 . .
=11,25кВ/м.
|
E = ?
|
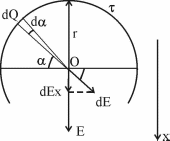
312. По тонкому полукольцу радиуса r = 10 см равномерно распределен заряд с линейной плотностью τ =1 мкКл/м. Определить напряженность Е электрического поля, создаваемого распределенным зарядом в точке О, совпадающей с центром кольца.
r =10 см
τ =1 мкКл/м
|
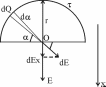
Заряд всего кольца равен 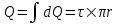 , где τ – линейная плотность. , где τ – линейная плотность.
Напряженность от заряда dQ = τ×r×dα в центре круга O, равна
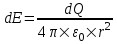 . .
Ввиду симметрии задачи, суммарная напряженность E будет направлена вдоль оси x, а другие проекции равны нулю.
Вклад в E дает только проекция вектора dE на ось x: 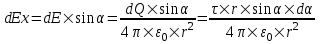 . .
Полная напряженность равна интегралу:
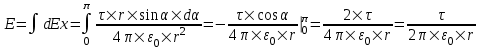 . .
Подставляем числа (переводя одновременно все величины в систему СИ).
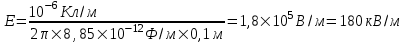 . .
|
E = ?
|
313. Тонкое кольцо несет распределенный заряд Q = 0,2 мкКл. Определить напряженность Е электрического поля, создаваемого распределенным зарядом в точке А, равноудаленной от всех точек кольца на расстояние R = 20 см. Радиус кольца r =10 см.
Q = 0,2 мкКл
r =10 см
R = 20 см
|
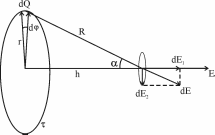
Заряд всего кольца равен 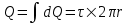 , где τ – линейная плотность. Откуда , где τ – линейная плотность. Откуда 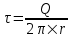 . .
Напряженность от заряда dQ = τ×r×dφ в точке, отстоящей на расстоянии R от кольца, равна 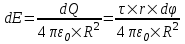 . .
Из рисунка видно, что проекции 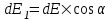 и и 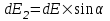 . Где . Где 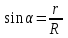 . Ввиду симметрии задачи сумма всех проекций . Ввиду симметрии задачи сумма всех проекций 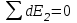 (см. рис.). Остальные проекции dE1 дают вклад в общую напряженность поля E. (см. рис.). Остальные проекции dE1 дают вклад в общую напряженность поля E.
Тогда 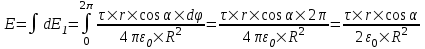 . .
Так как 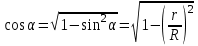 , то , то 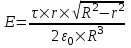 . Подставляем . Подставляем 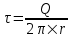 и тогда и тогда 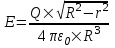 . .
Подставляем числа (переводя одновременно все величины в систему СИ). 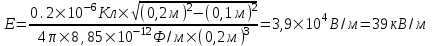
|
E = ?
|
314. Треть тонкого кольца радиуса r =10см несет распределенный заряд Q = 50нКл. Определить напряженность Е электрического поля, создаваемого распределенным зарядом в точке О, совпадающей с центром кольца.
r =10 см
Q = 50нКл
|
Заряд всего кольца (его трети) равен 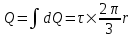 , где τ – линейная плотность. Откуда , где τ – линейная плотность. Откуда 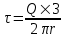 . .
Напряженность от заряда dQ = τ×r×dα в центре круга O, равна
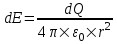 . .
Ввиду симметрии задачи, суммарная напряженность E будет направлена вдоль оси x, а другие проекции равны нулю.
Вклад в E дает только проекция вектора dE на ось x: 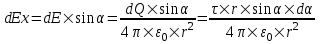 . .
Полная напряженность равна интегралу:
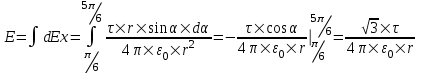 . .
Так как 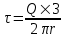 , то , то 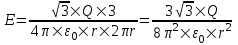
Подставляем числа (переводя одновременно все величины в систему СИ).
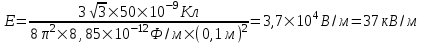 . .
|
E = ?
|
315. Бесконечный тонкий стержень, ограниченный с одной стороны, несет равномерно распределенный заряд с линейной плотностью ρ=0,5 мкКл/м. Определить напряженность Е электрического поля, создаваемого распределенным зарядом в точке А, лежащей на оси стержня на расстоянии а = 20 см от его начала.
a = 20 см
ρ=0,5мкКл/м
|

Определим напряженность dE, созданную элементарным зарядом dq=ρ×dr на расстоянии r (см. рис.) 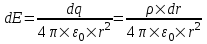 , где , где 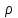 – линейная плотность зарядов стержня. Тогда полная напряженность равна интегралу – линейная плотность зарядов стержня. Тогда полная напряженность равна интегралу 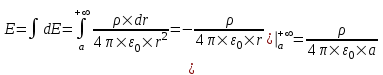 . .
Подставляем числа (переводя одновременно все величины в систему СИ). 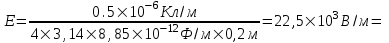 22,5кВ/м. 22,5кВ/м.
|
E = ?
|
316. По тонкому кольцу радиусом r = 20см равномерно распределен с линейной плотностью τ=0,2 мкКл/м заряд. Определить напряженность Е электрического поля, создаваемого распределенным зарядом в точке А, находящейся на оси кольца на расстоянии h = 2R от его центра.
τ=0,2 мкКл/м
r =10 см
h = 2r=20см
|

Заряд всего кольца равен 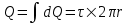 , где τ – линейная плотность. Напряженность от заряда dQ = τ×r×dφ в точке, отстоящей на расстоянии R от кольца, равна , где τ – линейная плотность. Напряженность от заряда dQ = τ×r×dφ в точке, отстоящей на расстоянии R от кольца, равна 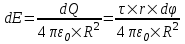 . .
Из рисунка видно, что проекции 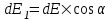 и и 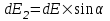 . Где . Где 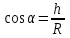 . Ввиду симметрии задачи сумма всех проекций . Ввиду симметрии задачи сумма всех проекций 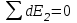 (см. рис.). Остальные проекции dE1 дают вклад в общую напряженность поля E. (см. рис.). Остальные проекции dE1 дают вклад в общую напряженность поля E.
Тогда 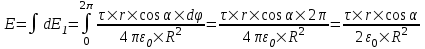 . .
Так как 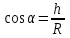 , то , то 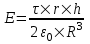 . Кроме того из рисунка видно, что . Кроме того из рисунка видно, что 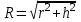 , поэтому , поэтому 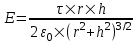 . .
Подставляем числа (переводя одновременно все величины в систему СИ). 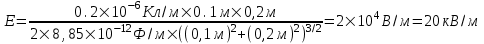 . .
|
E = ?
|
317. По тонкому полукольцу равномерно распределен заряд Q=20 мкКл с линейной плотностью τ=0,1 мкКл/м. Определить напряженность Е электрического поля, создаваемого распределенным зарядом в точке О, совпадающей с центром кольца.
Q=20 мкКл
τ=0,1 мкКл/м
|
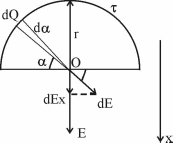
Заряд всего кольца равен 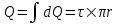 , где τ – линейная плотность. Откуда радиус кольца , где τ – линейная плотность. Откуда радиус кольца 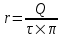 . .
Напряженность от заряда dQ = τ×r×dα в центре круга O, равна
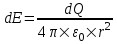 . .
Ввиду симметрии задачи, суммарная напряженность E будет направлена вдоль оси x, а другие проекции равны нулю.
Вклад в E дает только проекция вектора dE на ось x: 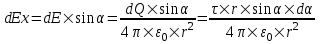 . .
Полная напряженность равна интегралу:
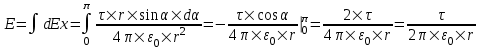 . Подставляем . Подставляем 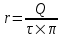 и получаем и получаем 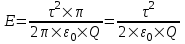 . .
Подставляем числа (переводя одновременно все величины в систему СИ).
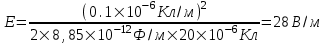 . .
|
E = ?
|
318. Четверть тонкого кольца радиусом r=10см несет равномерно распределенный заряд Q = 0,05мкКл. Определить напряженность Е электрического поля, создаваемого распределенным зарядом в точке О, совпадающей с центром кольца.
r =10 см
Q = 0.05мкКл
|
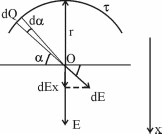
Заряд всего кольца (его четверти) равен 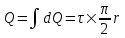 , где τ – линейная плотность. Откуда , где τ – линейная плотность. Откуда 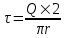 . .
Напряженность от заряда dQ = τ×r×dα в центре круга O, равна
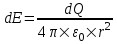 . .
Ввиду симметрии задачи, суммарная напряженность E будет направлена вдоль оси x, а другие проекции равны нулю.
Вклад в E дает только проекция вектора dE на ось x: 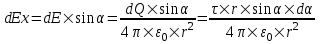 . .
Полная напряженность равна интегралу:
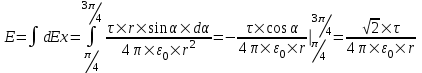 . .
Так как 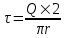 , то , то 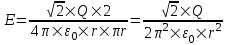
Подставляем числа (переводя одновременно все величины в систему СИ).
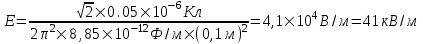 . .
|
E = ?
|
319. По тонкому кольцу равномерно распределен заряд Q=10 нКл с линейной плотностью τ=0,01 мкКл/м. Определить напряженность Е электрического поля, создаваемого распределенным зарядом в точке А, лежащей на оси кольца и удаленной от его центра на расстояние, равное радиусу кольца.
Q=10 нКл
τ=0,01мкКл/м
h = r
|

Заряд всего кольца равен 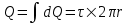 , где τ – линейная плотность. , где τ – линейная плотность.
Откуда радиус кольца равен 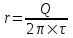 . .
Напряженность от заряда dQ = τ×r×dφ в точке, отстоящей на расстоянии R от кольца, равна 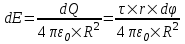 . .
Из рисунка видно, что проекции 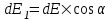 и и 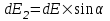 . Где . Где 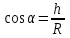 . Ввиду симметрии задачи сумма всех проекций . Ввиду симметрии задачи сумма всех проекций 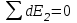 (см. рис.). Остальные проекции dE1 дают вклад в общую напряженность поля E. (см. рис.). Остальные проекции dE1 дают вклад в общую напряженность поля E.
Тогда 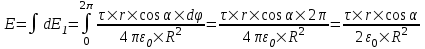 . .
Так как 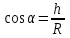 , то , то 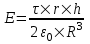 . Кроме того из рисунка видно, что . Кроме того из рисунка видно, что 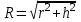 , поэтому , поэтому 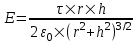 . Так как h=r, то . Так как h=r, то 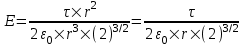 . Нам известен радиус . Нам известен радиус 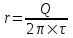 , поэтому , поэтому 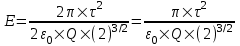 . .
Подставляем числа (переводя одновременно все величины в систему СИ). 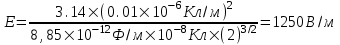 . .
|
E = ?
|
320. Две трети тонкого кольца радиусом r=10см несут равномерно распределенный с линейной плотностью τ=0,2 мкКл/м заряд. Определить напряженность Е электрического поля, создаваемого распределенным зарядом в точке О, совпадающей с центром кольца.
r =10 см
τ=0,2 мкКл/м
|
Заряд всего кольца (его две трети) равен 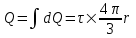 , где τ – линейная плотность. Откуда , где τ – линейная плотность. Откуда 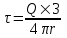 . .
Напряженность от заряда dQ = τ×r×dα в центре круга O, равна
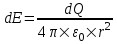 . .
Ввиду симметрии задачи, суммарная напряженность E будет направлена вдоль оси x, а другие проекции равны нулю.
Вклад в E дает только проекция вектора dE на ось x: 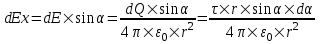 . .
Полная напряженность равна интегралу:
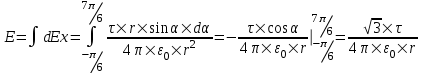 . .
Подставляем числа (переводя одновременно все величины в систему СИ).
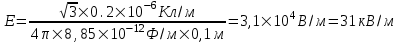 . .
|
E = ?
|
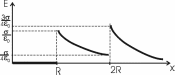
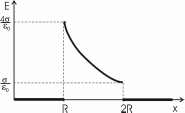
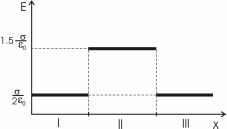
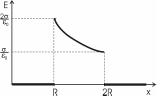
321. На двух концентрических сферах радиусом R и 2R равномерно распределены заряды с поверхностными плотностями σ1 и σ2 (рис.). Требуется: 1) используя теорему Остроградского—Гаусса, найти зависимость Е(x) напряженности электрического поля от расстояния для трех областей: I, II и III. Принять σ1=4σ, σ2 =σ; 2) вычислить напряженность Е в точке, удаленной от центра на расстояние r, и указать направление вектора Е. Принять σ=30 нКл/м2, r = l,5R; 3) построить график E(x).
R
2R
σ1=4σ
σ2 =σ
σ=30 нКл/м2
r = l,5R
|
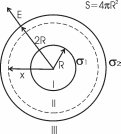 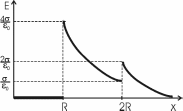
Воспользуемся теоремой Гаусса, согласно которой, поток напряженности E электрического поля через замкнутую поверхность S, с величиной заряда Q внутри этой поверхности, равен 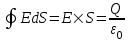 (в системе СИ), где ε0=8.85×10-12Ф/м – электрическая постоянная. В нашем случае площадь сферы на расстоянии x: S=4π×x2. Поэтому (в системе СИ), где ε0=8.85×10-12Ф/м – электрическая постоянная. В нашем случае площадь сферы на расстоянии x: S=4π×x2. Поэтому 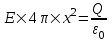 . Или же . Или же 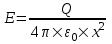 . Нам осталось найти заряд внутри сферы для трех разных случаев: . Нам осталось найти заряд внутри сферы для трех разных случаев:
0
R≤x<2R. В этом случае первая сфера целиком лежит внутри нашей поверхности и поэтому заряд равен Q=σ1×S1=σ1×4π×R2. Тогда 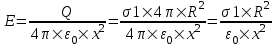 . В нашем случае σ1=4σ и поэтому . В нашем случае σ1=4σ и поэтому 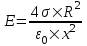 . .
Тогда 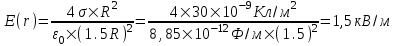 . .
2R≤x<+∞. В этом случае первая и вторая сфера целиком лежат внутри нашей поверхности и поэтому заряд равен
Q=σ1×S1+σ2×S2=σ1×4π×R2+σ2×4π×(2R)2.
Тогда 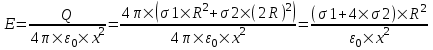 . В нашем случае σ1=σ и σ2=4σ поэтому . В нашем случае σ1=σ и σ2=4σ поэтому 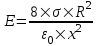 . .
|
E(x) = ?
E(r) = ?
|
322. На двух концентрических сферах радиусом R и 2R равномерно распределены заряды с поверхностными плотностями σ1 и σ2 (рис.). Требуется: 1) используя теорему Остроградского—Гаусса, найти зависимость Е(x) напряженности электрического поля от расстояния для трех областей: I, II и III. Принять σ1=σ, σ2 = –σ; 2) вычислить напряженность Е в точке, удаленной от центра на расстояние r, и указать направление вектора Е. Принять σ=0.1 мкКл/м2, r = 3R; 3) построить график E(x).
R
2R
σ1=σ
σ2 = –σ
σ=0,1мкКл/м2
r = 3R
|
Воспользуемся теоремой Гаусса, согласно которой, поток напряженности E электрического поля через замкнутую поверхность S, с величиной заряда Q внутри этой поверхности, равен 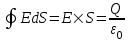 (в системе СИ), где ε0=8.85×10-12Ф/м – электрическая постоянная. В нашем случае площадь сферы на расстоянии x: S=4π×x2. Поэтому (в системе СИ), где ε0=8.85×10-12Ф/м – электрическая постоянная. В нашем случае площадь сферы на расстоянии x: S=4π×x2. Поэтому 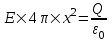 . Или же . Или же 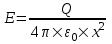 . Нам осталось найти заряд внутри сферы для трех разных случаев: . Нам осталось найти заряд внутри сферы для трех разных случаев:
0
R≤x<2R. В этом случае первая сфера целиком лежит внутри нашей поверхности и поэтому заряд равен Q=σ1×S1=σ1×4π×R2. Тогда 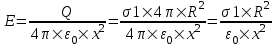 . В нашем случае σ1=σ и поэтому . В нашем случае σ1=σ и поэтому  . .
3) 2R≤x<+∞. В этом случае первая и вторая сфера целиком лежат внутри нашей поверхности и поэтому заряд равен
Q=σ1×S1+σ2×S2=σ1×4π×R2+σ2×4π×(2R)2.
Тогда 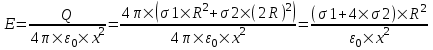 . В нашем случае σ1=σ и σ2=–σ поэтому . В нашем случае σ1=σ и σ2=–σ поэтому 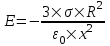 . Знак минус указывает на то, что поле в этой области направлено в противоположную сторону оси x. Но мы считаем только модуль и поэтому его знак минус нужно убрать. . Знак минус указывает на то, что поле в этой области направлено в противоположную сторону оси x. Но мы считаем только модуль и поэтому его знак минус нужно убрать.
Тогда 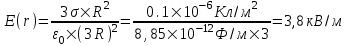 . .
|
E(x) = ?
E(r) = ?
|
323. На двух концентрических сферах радиусом R и 2R равномерно распределены заряды с поверхностными плотностями σ1 и σ2 (рис.). Требуется: 1) используя теорему Остроградского—Гаусса, найти зависимость Е(x) напряженности электрического поля от расстояния для трех областей: I, II и III. Принять σ1=–4σ, σ2 =σ; 2) вычислить напряженность Е в точке, удаленной от центра на расстояние r, и указать направление вектора Е. Принять σ=50 нКл/м2, r = 1,5R; 3) построить график E(x).
R
2R
σ1=–4σ
σ2 =σ
σ=50 нКл/м2
r = l,5R
|
Воспользуемся теоремой Гаусса, согласно которой, поток напряженности E электрического поля через замкнутую поверхность S, с величиной заряда Q внутри этой поверхности, равен 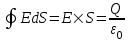 (в системе СИ), где ε0=8.85×10-12Ф/м – электрическая постоянная. В нашем случае площадь сферы на расстоянии x: S=4π×x2. Поэтому (в системе СИ), где ε0=8.85×10-12Ф/м – электрическая постоянная. В нашем случае площадь сферы на расстоянии x: S=4π×x2. Поэтому 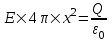 . Или же . Или же 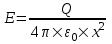 . Нам осталось найти заряд внутри сферы для трех разных случаев: . Нам осталось найти заряд внутри сферы для трех разных случаев:
0
R≤x<2R. В этом случае первая сфера целиком лежит внутри нашей поверхности и поэтому заряд равен Q=σ1×S1=σ1×4π×R2. Тогда 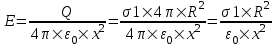 . В нашем случае σ1=–4σ и поэтому . В нашем случае σ1=–4σ и поэтому 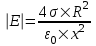 . .
Тогда 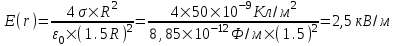 . .
2R≤x<+∞. В этом случае первая и вторая сфера целиком лежат внутри нашей поверхности и поэтому заряд равен
Q=σ1×S1+σ2×S2=σ1×4π×R2+σ2×4π×(2R)2.
Тогда 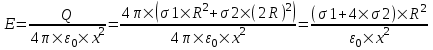 . В нашем случае σ1=–4σ и σ2=σ поэтому . В нашем случае σ1=–4σ и σ2=σ поэтому 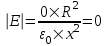 . То есть поля нет. . То есть поля нет.
|
E(x) = ?
E(r) = ?
|
324. На двух концентрических сферах радиусом R и 2R равномерно распределены заряды с поверхностными плотностями σ1 и σ2 (рис.). Требуется: 1) используя теорему Остроградского—Гаусса, найти зависимость Е(x) напряженности электрического поля от расстояния для трех областей: I, II и III. Принять σ1=–2σ, σ2 =σ; 2) вычислить напряженность Е в точке, удаленной от центра на расстояние r, и указать направление вектора Е. Принять σ=0.1 мкКл/м2, r = 3R; 3) построить график E(x).
R
2R
σ1=–2σ
σ2 = σ
σ=0,1мкКл/м2
r = 3R
|
Воспользуемся теоремой Гаусса, согласно которой, поток напряженности E электрического поля через замкнутую поверхность S, с величиной заряда Q внутри этой поверхности, равен 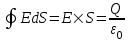 (в системе СИ), где ε0=8.85×10-12Ф/м – электрическая постоянная. В нашем случае площадь сферы на расстоянии x: S=4π×x2. Поэтому (в системе СИ), где ε0=8.85×10-12Ф/м – электрическая постоянная. В нашем случае площадь сферы на расстоянии x: S=4π×x2. Поэтому 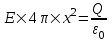 . Или же . Или же 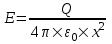 . Нам осталось найти заряд внутри сферы для трех разных случаев: . Нам осталось найти заряд внутри сферы для трех разных случаев:
0
R≤x<2R. В этом случае первая сфера целиком лежит внутри нашей поверхности и поэтому заряд равен Q=σ1×S1=σ1×4π×R2. Тогда 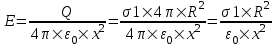 . В нашем случае σ1=–2σ и поэтому . В нашем случае σ1=–2σ и поэтому 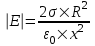 . .
3) 2R≤x<+∞. В этом случае первая и вторая сфера целиком лежат внутри нашей поверхности и поэтому заряд равен
Q=σ1×S1+σ2×S2=σ1×4π×R2+σ2×4π×(2R)2.
Тогда 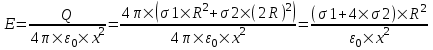 . В нашем случае σ1=–2σ и σ2=σ поэтому . В нашем случае σ1=–2σ и σ2=σ поэтому 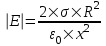 . .
Тогда 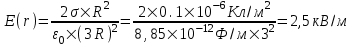 . .
|
E(x) = ?
E(r) = ?
|
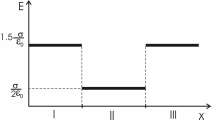
325. На двух бесконечных параллельных плоскостях равномерно распределены заряды с поверхностными плотностями σ1 и σ2. Требуется: 1) используя теорему Остроградского—Гаусса и принцип суперпозиции электрических полей, найти выражение Е(х) напряженности электрического поля в трех областях: I, II и III. Принять σ1 = 2σ, σ2 = σ; 2) вычислить напряженность Е поля в точке, расположенной слева от плоскостей, и указать направление вектора Е; 3) построить график Е(х).
σ1=2σ
σ2=σ
|
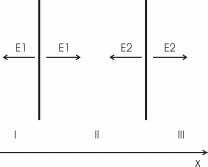
Воспользуемся принципом суперпозиции в каждой области.
В области I: E=E1+E2. Модуль 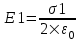 , модуль , модуль 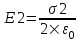 , поэтому E= , поэтому E=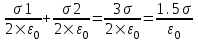 . В этой области поле отлично от нуля. . В этой области поле отлично от нуля.
В области II: E=E1–E2. поэтому E=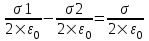 . .
В области III: E=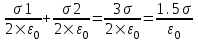 . В этой области поле отлично от нуля. . В этой области поле отлично от нуля.
Слева от плоскостей поле равно 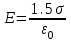 , и направлено влево (см. рис.). , и направлено влево (см. рис.).
|
E = ?
|
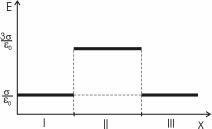
326. На двух бесконечных параллельных плоскостях равномерно распределены заряды с поверхностными плотностями σ1 и σ2. Требуется: 1) используя теорему Остроградского—Гаусса и принцип суперпозиции электрических полей, найти выражение Е(х) напряженности электрического поля в трех областях: I, II и III. Принять σ1=–4σ, σ2 =2σ; σ=40нКл/м2 2) вычислить напряженность Е поля в точке, расположенной между плоскостями, и указать направление вектора Е; 3) построить график Е(х).
σ1=–4σ
σ2=2σ
σ=40нКл/м2
|
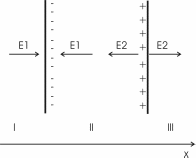
Воспользуемся принципом суперпозиции в каждой области.
В области I: E=E1–E2. Модуль 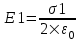 , модуль , модуль 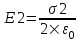 , поэтому , поэтому 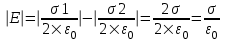 . В этой области поле отлично от нуля. . В этой области поле отлично от нуля.
В области II: E=E1+E2. поэтому 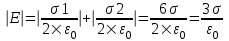 . .
В области III: E=E2–E1
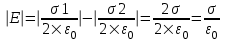 . В этой области поле отлично от нуля. . В этой области поле отлично от нуля.
Между плоскостями поле равно 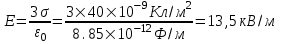 , и направлено влево (см. рис.). , и направлено влево (см. рис.).
|
E = ?
|
327. На двух бесконечных параллельных плоскостях равномерно распределены заряды с поверхностными плотностями σ1 и σ2. Требуется: 1) используя теорему Остроградского—Гаусса и принцип суперпозиции электрических полей, найти выражение Е(х) напряженности электрического поля в трех областях: I, II и III. Принять σ1=σ, σ2 =–2σ; σ=20нКл/м2 2) вычислить напряженность Е поля в точке, расположенной между плоскостями, и указать направление вектора Е; 3) построить график Е(х).
σ1=σ
σ2=–2σ
σ=20нКл/м2
|

Воспользуемся принципом суперпозиции в каждой области.
В области I: E=E1–E2. Модуль 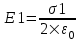 , модуль , модуль 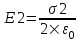 , поэтому , поэтому 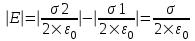 . В этой области поле отлично от нуля. . В этой области поле отлично от нуля.
В области II: E=E1+E2. поэтому 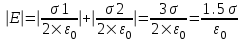 . .
В области III: E=E2–E1
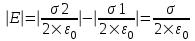 . В этой области поле отлично от нуля. . В этой области поле отлично от нуля.
Между плоскостями поле равно 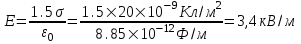 , и направлено вправо (см. рис.). , и направлено вправо (см. рис.).
|
E = ?
|
328. На двух коаксиальных бесконечных цилиндрах радиусами R и 2R равномерно распределены заряды с поверхностными плотностями σ1 и σ2. Требуется: 1) используя теорему Остроградского—Гаусса: найти зависимость E(x) напряженности электрического поля от расстояния для трех областей: I, II и III. Принять σ1 = –2σ, σ2 =σ; 2) вычислить напряженность Е в точке, удаленной от оси цилиндров на расстояние r, и указать направление вектора Е. Принять σ= 50 нКл/м2, r= 1,5R; 3) построить график E(x).
R
2R
σ1=–2σ
σ2 =σ
σ=50 нКл/м2
r = l,5R
|
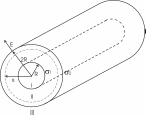 
Воспользуемся теоремой Гаусса, согласно которой, поток напряженности E электрического поля через замкнутую поверхность S, с величиной заряда Q внутри этой поверхности, равен 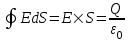 (в системе СИ), где ε0=8.85×10-12Ф/м – электрическая постоянная. Пусть этой поверхностью будет цилиндрический контур обозначенный пунктиром (см. рис.) (в системе СИ), где ε0=8.85×10-12Ф/м – электрическая постоянная. Пусть этой поверхностью будет цилиндрический контур обозначенный пунктиром (см. рис.)
В нашем случае площадь цилиндрического контура на расстоянии x: 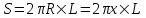 . Поэтому . Поэтому 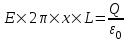 . Или же . Или же 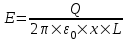 . Нам осталось найти заряд внутри цилиндра для трех разных случаев: . Нам осталось найти заряд внутри цилиндра для трех разных случаев:
0
R≤x<2R. В этом случае первый цилиндр целиком лежит внутри нашей поверхности и поэтому заряд равен Q=σ1×S1=σ1×2π×R×L. Тогда 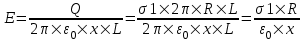 . В нашем случае σ1=–2σ и поэтому . В нашем случае σ1=–2σ и поэтому 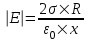 . .
Тогда 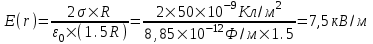 . .
2R≤x<+∞. В этом случае первый и второй цилиндры целиком лежат внутри нашей поверхности и поэтому заряд равен
Q=σ1×S1+σ2×S2=σ1×2π×R×L+ σ1×2π×2R×L.
Тогда 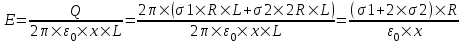 . .
В нашем случае σ1=–2σ и σ2=σ поэтому 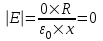 . То есть поля нет. . То есть поля нет.
|
E(x) = ?
E(r) = ?
| |
 Скачать 1.62 Mb.
Скачать 1.62 Mb.

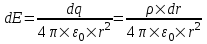 , где
, где 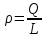 – линейная плотность зарядов стержня. Тогда полная напряженность равна интегралу
– линейная плотность зарядов стержня. Тогда полная напряженность равна интегралу 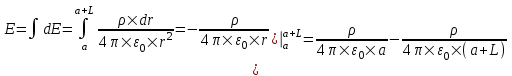 .
.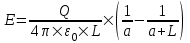 .
.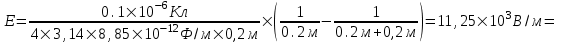 .
.
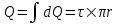 , где τ – линейная плотность.
, где τ – линейная плотность.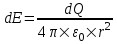 .
. 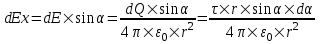 .
.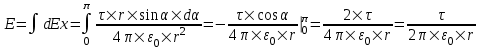 .
.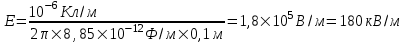 .
.
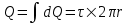 , где τ – линейная плотность. Откуда
, где τ – линейная плотность. Откуда 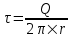 .
.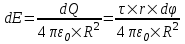 .
. 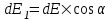 и
и 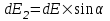 . Где
. Где 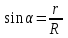 . Ввиду симметрии задачи сумма всех проекций
. Ввиду симметрии задачи сумма всех проекций 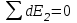 (см. рис.). Остальные проекции dE1 дают вклад в общую напряженность поля E.
(см. рис.). Остальные проекции dE1 дают вклад в общую напряженность поля E.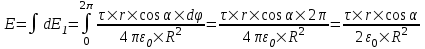 .
.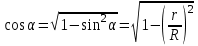 , то
, то 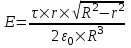 . Подставляем
. Подставляем 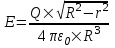 .
.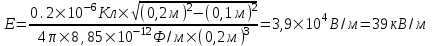

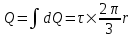 , где τ – линейная плотность. Откуда
, где τ – линейная плотность. Откуда 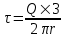 .
.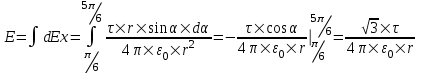 .
.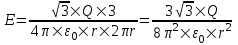
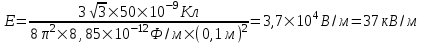 .
.
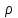 – линейная плотность зарядов стержня. Тогда полная напряженность равна интегралу
– линейная плотность зарядов стержня. Тогда полная напряженность равна интегралу 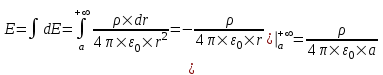 .
.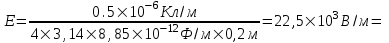 22,5кВ/м.
22,5кВ/м.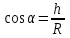 . Ввиду симметрии задачи сумма всех проекций
. Ввиду симметрии задачи сумма всех проекций 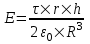 . Кроме того из рисунка видно, что
. Кроме того из рисунка видно, что 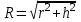 , поэтому
, поэтому 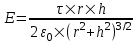 .
.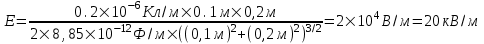 .
.
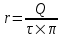 .
.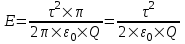 .
.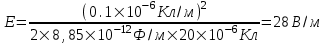 .
.
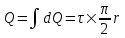 , где τ – линейная плотность. Откуда
, где τ – линейная плотность. Откуда 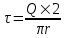 .
.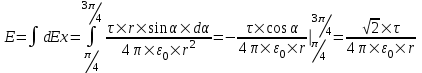 .
.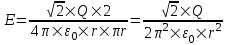
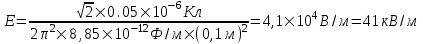 .
.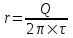 .
.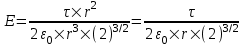 . Нам известен радиус
. Нам известен радиус 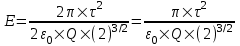 .
.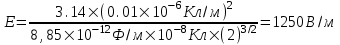 .
.
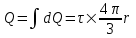 , где τ – линейная плотность. Откуда
, где τ – линейная плотность. Откуда 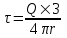 .
.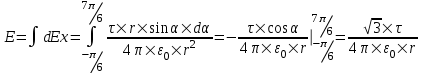 .
.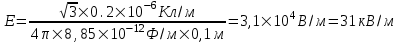 .
.

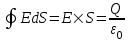 (в системе СИ), где ε0=8.85×10-12Ф/м – электрическая постоянная. В нашем случае площадь сферы на расстоянии x: S=4π×x2. Поэтому
(в системе СИ), где ε0=8.85×10-12Ф/м – электрическая постоянная. В нашем случае площадь сферы на расстоянии x: S=4π×x2. Поэтому 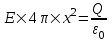 . Или же
. Или же 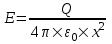 . Нам осталось найти заряд внутри сферы для трех разных случаев:
. Нам осталось найти заряд внутри сферы для трех разных случаев: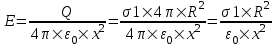 . В нашем случае σ1=4σ и поэтому
. В нашем случае σ1=4σ и поэтому 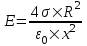 .
. 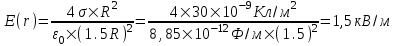 .
.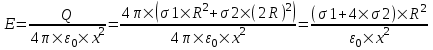 . В нашем случае σ1=σ и σ2=4σ поэтому
. В нашем случае σ1=σ и σ2=4σ поэтому 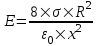 .
.
 .
. 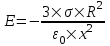 . Знак минус указывает на то, что поле в этой области направлено в противоположную сторону оси x. Но мы считаем только модуль и поэтому его знак минус нужно убрать.
. Знак минус указывает на то, что поле в этой области направлено в противоположную сторону оси x. Но мы считаем только модуль и поэтому его знак минус нужно убрать.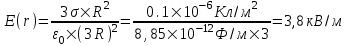 .
. 
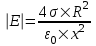 .
. 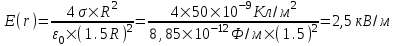 .
.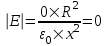 . То есть поля нет.
. То есть поля нет.
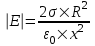 .
. 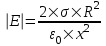 .
. 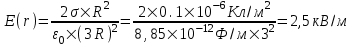 .
. 
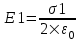 , модуль
, модуль 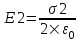 , поэтому E=
, поэтому E=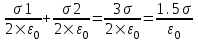 . В этой области поле отлично от нуля.
. В этой области поле отлично от нуля.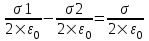 .
. 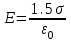 , и направлено влево (см. рис.).
, и направлено влево (см. рис.).

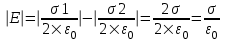 . В этой области поле отлично от нуля.
. В этой области поле отлично от нуля.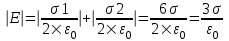 .
. 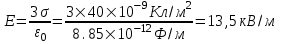 , и направлено влево (см. рис.).
, и направлено влево (см. рис.). 

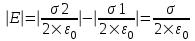 . В этой области поле отлично от нуля.
. В этой области поле отлично от нуля.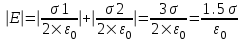 .
. 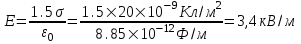 , и направлено вправо (см. рис.).
, и направлено вправо (см. рис.). 


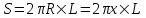 . Поэтому
. Поэтому 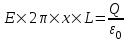 . Или же
. Или же 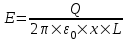 . Нам осталось найти заряд внутри цилиндра для трех разных случаев:
. Нам осталось найти заряд внутри цилиндра для трех разных случаев: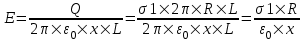 . В нашем случае σ1=–2σ и поэтому
. В нашем случае σ1=–2σ и поэтому 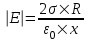 .
. 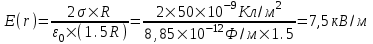 .
.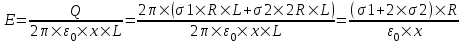 .
. 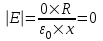 . То есть поля нет.
. То есть поля нет.