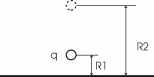
339. Электрическое поле образовано бесконечно длинной нитью, заряженной с линейной плотностью τ=20 пКл/м. Определить разность потенциалов U двух точек поля, отстоящих от нити на расстоянии R1=8 см и R2= 12 см.
τ = 20 пКл/м
R1 = 8 cм R2 = 12 cм |
Известно, что напряженность равномерно заряженной бесконечной нити 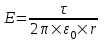 . Поэтому потенциал поля от равномерно заряженной бесконечной плоскости . Поэтому потенциал поля от равномерно заряженной бесконечной плоскости 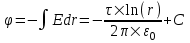 , где C – постоянная интегрирования. , где C – постоянная интегрирования.
Тогда разность потенциалов равна
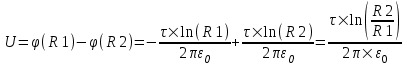 . .
Подставляем числа (переводя одновременно все величины в систему СИ). 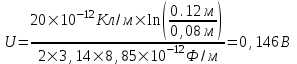 . .
|
U = ?
|
340. Тонкая квадратная рамка равномерно заряжена с линейной плотностью заряда τ=200пКл/м. Определить потенциал φ поля в точке пересечения диагоналей.
τ=200пКл/м
|
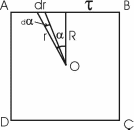
Найдем потенциал от отрезка AB (см. рис.).
Потенциал в точке O от участка dr, который имеет заряд τ×dr, равен 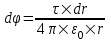 . Из рисунка видно, что dr = r×dα, поэтому . Из рисунка видно, что dr = r×dα, поэтому 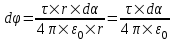 . Тогда полный потенциал от отрезка AB равен интегралу . Тогда полный потенциал от отрезка AB равен интегралу 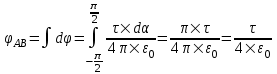 . .
В виду симметрии задачи потенциал от всей рамки равен φ=4×φAB. Тогда 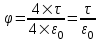 . .
Подставляем числа (переводя одновременно все величины в систему СИ).
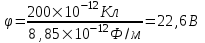 . .
|
φ = ?
|
341. Пылинка массой m=200 мкг, несущая на себе заряд Q = 40 нКл, влетела в электрическое поле в направлении силовых линий. После прохождения разности потенциалов U=200 В пылинка имела скорость V2 = 10 м/с. Определить скорость пылинки до того, как она влетела в поле.
V2 = 10м/с
Q = 40 нКл
m=200 мкг
U=200 В
|
Из закона сохранения энергии имеем: T1+W=T2, где 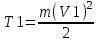 - начальная кинетическая энергия пылинки, W=Q×U - потенциальная энергия пылинки, проходящей через разность потенциалов U, - начальная кинетическая энергия пылинки, W=Q×U - потенциальная энергия пылинки, проходящей через разность потенциалов U, 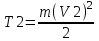 - конечная кинетическая энергия пылинки. - конечная кинетическая энергия пылинки.
Поэтому 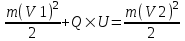 , откуда искомая скорость , откуда искомая скорость 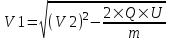 . Подставляем числа (переводя одновременно все величины в систему СИ). . Подставляем числа (переводя одновременно все величины в систему СИ).
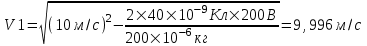 . .
|
V1 = ?
|
342. Электрон, обладавший кинетической энергией Т =10 эВ, влетел в однородное электрическое поле в направлении силовых линий поля. Какой скоростью будет обладать электрон, пройдя в этом поле разность потенциалов U = 8 В?
T1=10эВ
U=8 В
|
Из закона сохранения энергии имеем: T1+W=T2, где 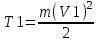 - начальная кинетическая энергия электрона, W=Q×U - потенциальная энергия электрона, проходящей через разность потенциалов U, - начальная кинетическая энергия электрона, W=Q×U - потенциальная энергия электрона, проходящей через разность потенциалов U, 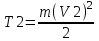 - конечная кинетическая энергия электрона. - конечная кинетическая энергия электрона.
Поэтому 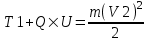 , откуда искомая скорость , откуда искомая скорость 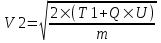 . Подставляем числа (переводя одновременно все величины в систему СИ). . Подставляем числа (переводя одновременно все величины в систему СИ).
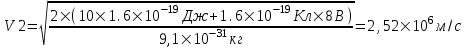 . .
|
V2 = ?
|
343. Найти отношение скоростей ионов Сu++ и Na+, прошедших одинаковую разность потенциалов.
U1 = U2
Q1=2×Q2
M1=63.5г/моль
M2=39г/моль
|
Потенциальная энергия заряда, который прошел потенциал U, равна 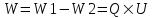 . .
Воспользуемся законом сохранения энергии: Ek1+W1=Ek2+W2, где Ek1=0 – начальная кинетическая энергия заряда,  – кинетическая энергия электрона после прохождения потенциала U. – кинетическая энергия электрона после прохождения потенциала U.
Поэтому 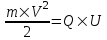 . .
Отсюда находим скорость  . .
Тогда отношение скоростей равно 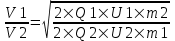 . Так как U1=U2 и Q1=2×Q2, то . Так как U1=U2 и Q1=2×Q2, то 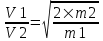 . .
Массу атомов найдем из формулы 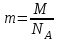 , где M - молярная масса атома, NA – число Авогадро. Поэтому , где M - молярная масса атома, NA – число Авогадро. Поэтому 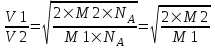 . .
Подставляем числа. 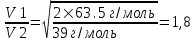 . .
|
V1/V2 = ?
|
344. Электрон с энергией T=400 эВ (в бесконечности) движется вдоль силовой линии по направлению к поверхности металлической заряженной сферы радиусом R = 10 см. Определить минимальное расстояние, на которое приблизится электрон к поверхности сферы, если заряд ее Q = – 10 нКл.
T=400 эВ
R = 10 см
Q = – 10 нКл
|
Потенциал, который создает заряженная сфера радиусом R, на расстоянии x от ее поверхности равен 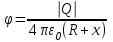 . .
Потенциальная энергия электрона тогда равна 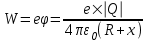 . .
Воспользуемся законом сохранения энергии: Ek1+W1=Ek2+W2, где Ek1=T – кинетическая энергия электрона на бесконечности, 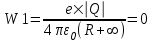 - потенциальная энергия электрона на бесконечности, Ek2=0 – кинетическая энергия электрона на расстоянии x (он остановился и его скорость равна 0), - потенциальная энергия электрона на бесконечности, Ek2=0 – кинетическая энергия электрона на расстоянии x (он остановился и его скорость равна 0), 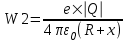 - потенциальная энергия электрона на расстоянии x. Поэтому - потенциальная энергия электрона на расстоянии x. Поэтому 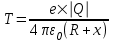 . Откуда . Откуда 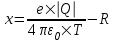 . Подставляем числа (переводя одновременно все величины в систему СИ). . Подставляем числа (переводя одновременно все величины в систему СИ). 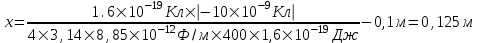 . .
|
x = ?
|
352. Конденсатор емкостью C1 = 10 мкФ заряжен до напряжения U1 = 10 В. Определить заряд на обкладках этого конденсатора после того, как параллельно ему был подключен другой, незаряженный, конденсатор емкостью С2 = 20 мкФ.
C1=10 мкФ
C2=20 мкФ
Q2=0
U1=10 В
параллельно
|
Заряд конденсатора емкостью C равен Q=C×U.
Тогда Q1=C1×U1=C×U1 и Q2=C2×U2=C×U2.
Когда конденсаторы соединяются параллельно одноименно заряженными обкладками и тогда общий заряд на пластинах станет Q=Q1+Q2. Так как второй конденсатор незаряжен (Q2=0), то Q1=Q.
Конденсаторы соединены параллельно, поэтому емкость такой батареи конденсаторов равна С=С1+С2, а напряжение U=U1. Поэтому заряд равен  . .
Подставляем числа.  . .
|
Q1=?
|
353. Конденсаторы емкостями С1 = 2 мкФ, С2 = 15 мкФ и С3 =10 мкФ соединены последовательно и находятся под напряжением U = 850 В. Определить напряжение и заряд на каждом из конденсаторов.
С1 = 2 мкФ
С2 = 15 мкФ
С3 =10 мкФ
U=850В
|
Так как конденсаторы соединены последовательно, то заряды равны друг другу Q1=Q2=Q3=Q.
Конденсаторы соединены последовательно, поэтому емкость такой батареи конденсаторов находится из уравнения  , то есть , то есть 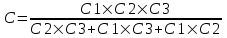 . .
Заряд Q по определению равен Q=C×U, где U – напряжение. Поэтому  . Подставляем числа. . Подставляем числа. 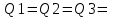 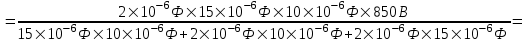
=1,275×10-3Кл.
Так как заряд на конденсаторе равен Q=C×U, то 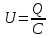 , откуда для первого конденсатора , откуда для первого конденсатора 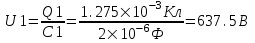 , для второго конденсатора , для второго конденсатора 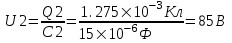 , а для третьего , а для третьего 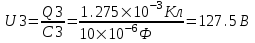 . .
|
Q1=?
Q2=?
Q3=?
U1 =?
U2 =?
U3=?
|
354. Два конденсатора емкостями С1 = 2 мкФ и С2 = 5 мкФ заряжены до напряжений U1=100 В и U2 =150 В соответственно. Определить напряжение на обкладках конденсаторов после их соединения обкладками, имеющими разноименные заряды.
C1=2 мкФ
C2=5 мкФ
U1=100 В
U2=150 В
разноименно
|
Заряд конденсатора емкостью C равен Q=C×U.
Тогда Q1=C1×U1=C×U1 и Q2=C2×U2=C×U2.
Когда конденсаторы соединяются параллельно разноименно заряженными обкладками общий заряд на пластинах станет Q=Q2–Q1. Конденсаторы соединены параллельно, поэтому емкость такой батареи конденсаторов равна С=С1+С2. Поэтому напряжение равно 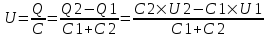 . .
Подставляем числа. 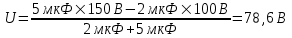 . .
|
U=?
|
355. Два одинаковых плоских воздушных конденсатора емкостью С = 100 пФ каждый соединены в батарею последовательно. Определить, на сколько изменится емкость С батареи, если пространство между пластинами одного из конденсаторов заполнить парафином.
ε=2
С=100 пФ
|
Обозначим электроемкость каждого конденсатора через С. Из электростатики известно, что электроемкость плоского конденсатора пропорциональна диэлектрической проницаемости ε диэлектрика между пластинами, конденсатора. Следовательно, после заполнения одного из конденсаторов парафином, его электроемкость станет равной εС. Обозначим через С1, С2 суммарные электрические емкости пары конденсаторов до и после погружения одного из них в масло соответственно. Поскольку суммарная электроемкость цепи последовательно соединенных конденсаторов равна среднему гармоническому из электроемкостей конденсаторов этой цепи, то
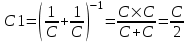 , и , и 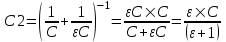 . .
Поэтому разность равна 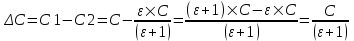 . .
Подставляем числа. 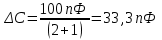 . .
|
ΔC=?
|
356. Два конденсатора емкостью С1 = 5 мкф и С2 = 8 мкф соединены последовательно и присоединены к батарее с э.д.с. ε=80В. Определить заряд Q1 и Q2 каждого из конденсаторов и разности потенциалов U1 и U2 между их обкладками.
С1 = 5 мкф
С2 = 8 мкф
ε=80В
|
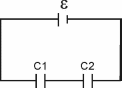
Так как конденсаторы соединены последовательно, то заряды равны друг другу Q1=Q2=Q.
Конденсаторы соединены последовательно, поэтому емкость такой батареи конденсаторов находится из уравнения 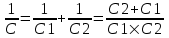 , то есть , то есть 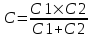 . .
Заряд Q по определению равен Q=C×U, где U=ε – потенциал э.д.с. Поэтому 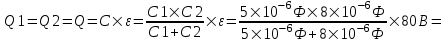
=2,46×10-4Кл.
Так как заряд на конденсаторе равен Q=C×U, то 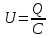 , откуда для первого конденсатора , откуда для первого конденсатора 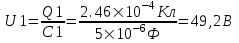 , а для второго конденсатора , а для второго конденсатора  . .
|
Q1 = ?
Q2 = ?
U1 = ?
U2 = ?
|
357. Плоский конденсатор состоит из двух круглых пластин радиусом R = 10 см каждая. Расстояние между пластинами d = 2 мм. Конденсатор присоединен к источнику напряжения U=80В. Определить заряд и напряженность поля конденсатора, если диэлектриком будут: а) воздух; б) стекло.
U = 80В
R = 10 см
d = 2 мм
ε1 = 1
ε2 = 1.5
|
Известно, что емкость плоского конденсатора 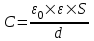 , где ε – диэлектрическая проницаемость диэлектрика (в нашем случае ε1=1 – для воздуха, ε2=1.5 – для стекла), d – расстояние между пластинами, S - площадь пластин, ε0= , где ε – диэлектрическая проницаемость диэлектрика (в нашем случае ε1=1 – для воздуха, ε2=1.5 – для стекла), d – расстояние между пластинами, S - площадь пластин, ε0=  - электрическая постоянная. - электрическая постоянная.
Так как пластины круглые, то их площадь равна S=π×R2. Поэтому 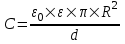 . .
С другой стороны известно, что 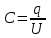 , где q – заряд на пластинах, U – приложенное напряжение. Поэтому , где q – заряд на пластинах, U – приложенное напряжение. Поэтому 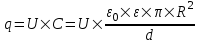 . .
Откуда для ε1=1 имеем
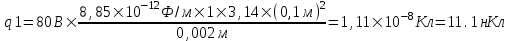 . .
Для ε2=1,5 имеем 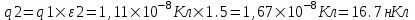 . .
Напряженность поля по определению равно 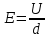 . Оно будет постоянно при любой среде между обкладками, если всегда поддерживается постоянная разность потенциала U, поэтому . Оно будет постоянно при любой среде между обкладками, если всегда поддерживается постоянная разность потенциала U, поэтому 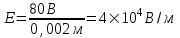 . .
|
q1 = ?
q2 = ?
E1 = ?
E2 = ?
|
358. Два металлических шарика радиусами R1=5 см и R2 = 10 см имеют заряды Q1 = 40 нКл и
Q2=–20нКл соответственно. Найти энергию W, которая выделится при разряде, если шары соединить проводником.
R1 = 5 см
R2 = 10 см
Q1=40 нКл
Q2=–20нКл
|
Выделившаяся энергия равна A=I×U×T, где I – сила прошедшего тока, U - разность потенциалов, T – время разряда.
С другой стороны произведение тока на время равно общему количеству прошедшего через проводник заряда. Поэтому I×U=ΔQ и тогда A=U×ΔQ.
Заряд на первом шарике Q1, а на втором Q2. После их соединения их общий заряд стал Q=Q1+Q2, и тогда на каждом из них заряд равен 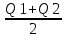 . Поэтому изменение заряда равно . Поэтому изменение заряда равно 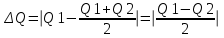 . .
Разность потенциалов между шариками равна φ=φ1–φ2= . .
Поэтому искомая энергия равна
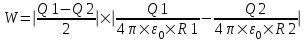 . .
Подставляем числа (переводя одновременно все величины в систему СИ).
|
W= ?
|
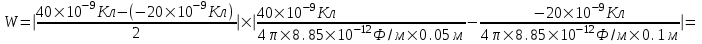
=2,7×10-4Дж=270мкДж.
|
 Скачать 1.62 Mb.
Скачать 1.62 Mb.


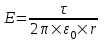 . Поэтому потенциал поля от равномерно заряженной бесконечной плоскости
. Поэтому потенциал поля от равномерно заряженной бесконечной плоскости 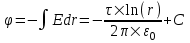 , где C – постоянная интегрирования.
, где C – постоянная интегрирования.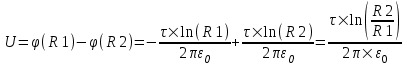 .
.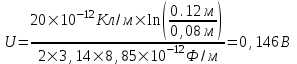 .
.
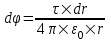 . Из рисунка видно, что dr = r×dα, поэтому
. Из рисунка видно, что dr = r×dα, поэтому 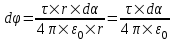 . Тогда полный потенциал от отрезка AB равен интегралу
. Тогда полный потенциал от отрезка AB равен интегралу 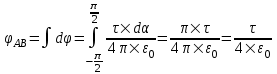 .
.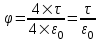 .
.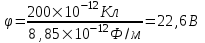 .
.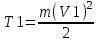 - начальная кинетическая энергия пылинки, W=Q×U -
- начальная кинетическая энергия пылинки, W=Q×U - 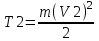 - конечная кинетическая энергия пылинки.
- конечная кинетическая энергия пылинки. 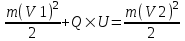 , откуда искомая скорость
, откуда искомая скорость 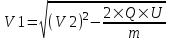 . Подставляем числа (переводя одновременно все величины в систему СИ).
. Подставляем числа (переводя одновременно все величины в систему СИ).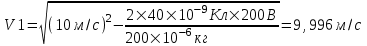 .
.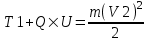 , откуда искомая скорость
, откуда искомая скорость 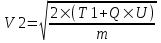 . Подставляем числа (переводя одновременно все величины в систему СИ).
. Подставляем числа (переводя одновременно все величины в систему СИ).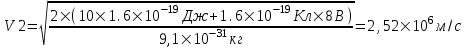 .
.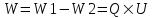 .
. – кинетическая энергия электрона после прохождения потенциала U.
– кинетическая энергия электрона после прохождения потенциала U.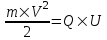 .
.  .
. 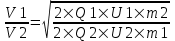 . Так как U1=U2 и Q1=2×Q2, то
. Так как U1=U2 и Q1=2×Q2, то 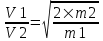 .
.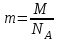 , где M - молярная масса атома, NA – число Авогадро. Поэтому
, где M - молярная масса атома, NA – число Авогадро. Поэтому 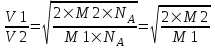 .
.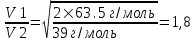 .
.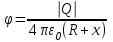 .
.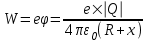 .
.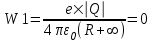 - потенциальная энергия электрона на бесконечности, Ek2=0 – кинетическая энергия электрона на расстоянии x (он остановился и его скорость равна 0),
- потенциальная энергия электрона на бесконечности, Ek2=0 – кинетическая энергия электрона на расстоянии x (он остановился и его скорость равна 0), 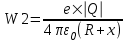 - потенциальная энергия электрона на расстоянии x. Поэтому
- потенциальная энергия электрона на расстоянии x. Поэтому 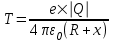 . Откуда
. Откуда 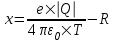 . Подставляем числа (переводя одновременно все величины в систему СИ).
. Подставляем числа (переводя одновременно все величины в систему СИ). 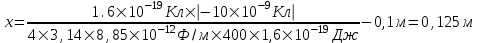 .
. .
. .
. , то есть
, то есть 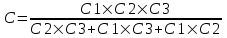 .
. . Подставляем числа.
. Подставляем числа. 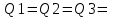
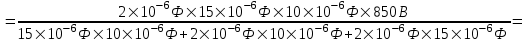
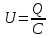 , откуда для первого конденсатора
, откуда для первого конденсатора 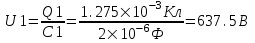 , для второго конденсатора
, для второго конденсатора 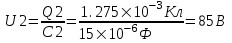 , а для третьего
, а для третьего 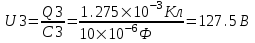 .
.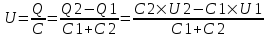 .
.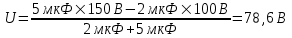 .
.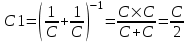 , и
, и 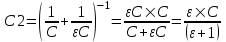 .
.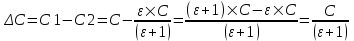 .
.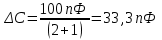 .
.
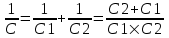 , то есть
, то есть 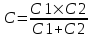 .
.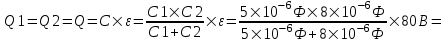
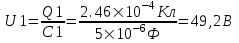 , а для второго конденсатора
, а для второго конденсатора  .
.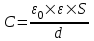 , где ε – диэлектрическая проницаемость диэлектрика (в нашем случае ε1=1 – для воздуха, ε2=1.5 – для стекла), d – расстояние между пластинами, S - площадь пластин, ε0=
, где ε – диэлектрическая проницаемость диэлектрика (в нашем случае ε1=1 – для воздуха, ε2=1.5 – для стекла), d – расстояние между пластинами, S - площадь пластин, ε0=  - электрическая постоянная.
- электрическая постоянная. 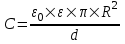 .
.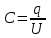 , где q – заряд на пластинах, U – приложенное напряжение. Поэтому
, где q – заряд на пластинах, U – приложенное напряжение. Поэтому 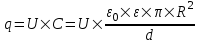 .
.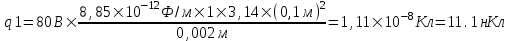 .
.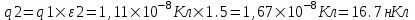 .
.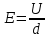 . Оно будет постоянно при любой среде между обкладками, если всегда поддерживается постоянная разность потенциала U, поэтому
. Оно будет постоянно при любой среде между обкладками, если всегда поддерживается постоянная разность потенциала U, поэтому 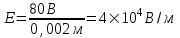 .
.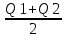 . Поэтому изменение заряда равно
. Поэтому изменение заряда равно 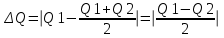 .
. .
.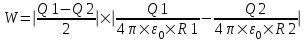 .
.