301. Точечные заряды q1=20 мкКл и q2= –10 мкКл находятся на расстоянии R = 5 см друг от друга. Определить напряженность поля в точке, удаленной на L1 = 3 см от первого и L2=4 см от второго заряда. Определить также силу F, действующую в этой точке на точечный заряд q= 1мкКл.
R = 5 cм
L1 = 3 cм
L2 = 4 cм
q1 = 20 мкКл
q2 =-10 мкКл
q =1 мкКл
|
Э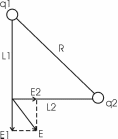 ти три точки образуют прямоугольный треугольник т.к. L12+L22=R2. ти три точки образуют прямоугольный треугольник т.к. L12+L22=R2.
Напряженность поля точечного заряда q на расстоянии r: 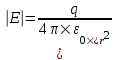 . .
Поэтому напряженность поля от первого заряда q1 на расстоянии L1: 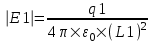 , а от второго , а от второго 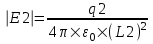 . .
Пользуясь принципом суперпозиции получаем 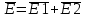 (Это векторные величины, а нам нужны скалярные). Поскольку угол между E1 и E2 прямой (так как треугольник прямоугольный), то по теореме Пифагора (Это векторные величины, а нам нужны скалярные). Поскольку угол между E1 и E2 прямой (так как треугольник прямоугольный), то по теореме Пифагора
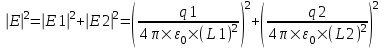 . .
Откуда 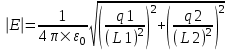
Подставляем числа
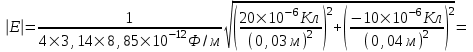
=2.1×108 В/м = 210 МВ/м.
Сила действующая на заряд q будет направлена по полю E и равна по модулю величине 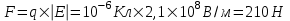 . .
|
E = ?
F = ?
|
302. Три одинаковых точечных заряда q1 = q2= q3 =2 нКл находятся в вершинах равностороннего треугольника со сторонами а=10см. Определить модуль и направление силы F, действующей на один из зарядов со стороны двух других.
q1=q2=q3=q=2нКл
a = 10 cм
|

Сила с которой действует заряд q1 на заряд q2 определяется из закона Кулона: 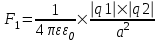 , где ε – диэлектрическая постоянная. В нашем случае она равна ε=1. , где ε – диэлектрическая постоянная. В нашем случае она равна ε=1.
В нашем случае заряды и расстояния между ними одинаковы, поэтому сила F1=F2=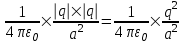 . .
Из рисунка видно, что искомая сила F=F3=2×F1×cos30º (так как угол треугольника равен 60º, а сила F направлена по биссектрисе этого угла).
Поэтому 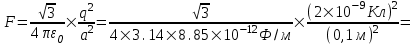
=6,23×10-6Н=6,23мкН.
|
F = ?
|
303. Два положительных точечных заряда q1=Q и q2=9Q закреплены на расстоянии L=100см друг от друга. Определить, в какой точке на прямой, проходящей через заряды, следует поместить третий заряд так, чтобы он находился в равновесии. Указать, какой знак должен иметь этот заряд для того, чтобы равновесие было устойчивым, если перемещения зарядов возможны только вдоль прямой, проходящей через закрепленные заряды.
q1=Q
q2=9Q
L = 100 см
|
И з рисунка видно, что если заряд q будет слева или справа от обоих зарядов, то силы будут направлены в одну сторону и устойчивого положения нет. Оно возможно только когда заряд находится между q1 и q2 (см нижний рисунок). з рисунка видно, что если заряд q будет слева или справа от обоих зарядов, то силы будут направлены в одну сторону и устойчивого положения нет. Оно возможно только когда заряд находится между q1 и q2 (см нижний рисунок).
Силу взаимодействия определим из закона Кулона: 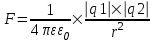 . .
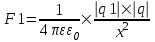 , , 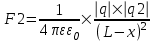 . Эти силы должны быть противоположны по направлению и одинаковыми по модулю (3-й закон Ньютона). Тогда . Эти силы должны быть противоположны по направлению и одинаковыми по модулю (3-й закон Ньютона). Тогда 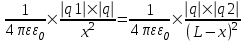 . Откуда . Откуда  . Откуда . Откуда  . Искомая величина равна . Искомая величина равна 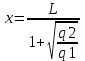 . Подставляем числа (переводя одновременно все величины в систему СИ). . Подставляем числа (переводя одновременно все величины в систему СИ).  . .
То есть между зарядами на расстоянии 25 см от заряда q1.
|
x = ?
|
Определим знак заряда q, при котором равновесие будет устойчивым. Равновесие называется устойчивым, если при смещении заряда от положения равновесия возникают силы, возвращающие его в положение равновесия. Рассмотрим смещение заряда q в двух случаях: когда заряд положителен и отрицателен.
Если заряд q положителен, то при смещении его влево сила F1возрастает, а сила F2 убывает. Результирующая сила, действующая на заряд q, будет направлена в противоположную сторону, в которую смещен этот заряд, т. е. вправо. Под действием этой силы заряд q будет возвращаться в положение равновесия. То же происходит и при смещении заряда q вправо. Сила F1убывает, а F2 возрастает.Геометрическая сумма сил в этом случае направлена влево. Заряд под действием этой силы будет перемещаться влево, т. е. возвращаться в положение равновесия. Таким образом, в случае положительного заряда равновесие является устойчивым. Если заряд q отрицателен, то при смещении его влево сила F1 будет направлена влево и будетвозрастать, а сила F2 убывать. Результирующая сила, действующая на заряд q, будет направлена в ту же сторону, в которую смещен этот заряд, т. е. влево. Под действием этой силы заряд q будет уходить от положения равновесия. То же происходит и при смещении заряда q вправо. Заряд будет уходить от положение равновесия. Таким образом, в случае положительного заряда равновесие является неустойчивым.
304. Два одинаково заряженных шарика подвешены в одной точке на нитях одинаковой длины. При этом нити разошлись на угол α. Шарики погружают в масло. Какова плотность ρ0 масла, если угол расхождения нитей при погружении в масло остается неизменным? Плотность материала шариков ρ=1,5×103 кг/м3, диэлектрическая проницаемость масла ε=2,2.
m1=m2=m
q1=q2=q
L
α
ρ=1.5×103 кг/м3
ε=2.2
|
Н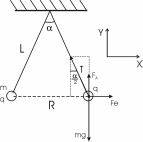 а каждый заряд действуют четыре силы: а каждый заряд действуют четыре силы: 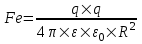 – сила Кулона, mg – сила притяжения, T – сила натяжения нити и сила Архимеда FA. Так как заряды находятся в равновесии, то из третьего закона Ньютона получаем, что сумма всех сил действующих на заряд равна нулю. Поэтому суммы сил – сила Кулона, mg – сила притяжения, T – сила натяжения нити и сила Архимеда FA. Так как заряды находятся в равновесии, то из третьего закона Ньютона получаем, что сумма всех сил действующих на заряд равна нулю. Поэтому суммы сил
проектируемые на ось X и ось Y тоже равны нулю:
на X: T×sin(α/2) =Fe
на Y: T×cos(α/2) =mg–FA.
Делим первое на второе и получаем 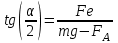 - условие равновесия заряда. Сила Архимеда равна - условие равновесия заряда. Сила Архимеда равна 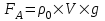 , где V – объем шарика. Тогда масса шарика равна m=ρ×V. Поэтому , где V – объем шарика. Тогда масса шарика равна m=ρ×V. Поэтому 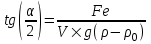 . .
В случае когда шарик находится в воздухе (ε=1 – диэлектрическая проницаемость и ρ0=0 – плотность воздуха почти ноль) имеем 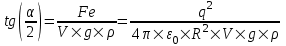 . .
В случае когда шарик находится в масле имеем
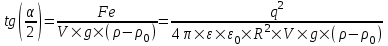 . .
Так как углы α равны, то
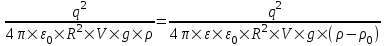
Откуда искомая величина  . Подставляем числа. . Подставляем числа. 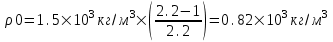 . .
|
ρ0 = ?
|
305. Четыре одинаковых заряда q1=q2=q3=q4 = 40нКл закреплены в вершинах квадрата со стороной а= 10 см. Найти силу F, действующую на один из этих зарядов со стороны трех остальных.
q1=q2=q3=q=40нКл
a = 10 cм
|
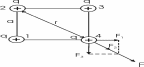
Сила с которой действует заряд q1 на заряд q4 определяется из закона Кулона: 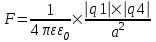 , где ε – диэлектрическая постоянная. В нашем случае она равна ε=1. , где ε – диэлектрическая постоянная. В нашем случае она равна ε=1.
В нашем случае все заряды одинаковы, поэтому сила F1=F3=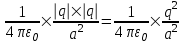 . .
Из рисунка видно, что искомая сила F=F2+F3=F2+2×F1×cos45º (так как сила F направлена по биссектрисе угла).
Сила с которой действует заряд q2 на заряд q4 равна:  . (Здесь . (Здесь 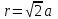 как видно из рисунка). как видно из рисунка).
Подставляем в F= F2+2×F1×cos45º и получаем
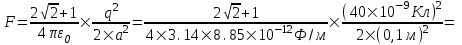
=2,76×10-3Н=2,76мН.
|
F = ?
|
306. Точечные заряды q1=30 мкКл и q2= –20 мкКл находятся на расстоянии R= 20 см друг от друга. Определить напряженность электрического поля Е в точке, удаленной от первого заряда на расстояние L1 = 30 см, a от второго – на L2= 15 см.
R=20 cм
L1=30 cм
L2=15 cм
q1=30мкКл
q2=
–20мкКл
|
Напряженность поля точечного заряда q на расстоянии r: 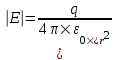 . .
Поэтому напряженность поля от первого заряда q1 на расстоянии L1: 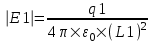 , а от второго , а от второго 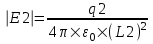 . .
Пользуясь принципом суперпозиции получаем 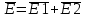 (Это векторные величины, а нам нужны скалярные). (Это векторные величины, а нам нужны скалярные).
Модуль вектора E найдем по теореме косинусов:

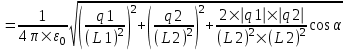 . .
З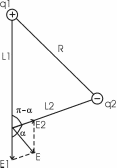 десь угол α – угол между векторами E1 и E2, который может быть найден из треугольника со сторонами L1, L2 и R: десь угол α – угол между векторами E1 и E2, который может быть найден из треугольника со сторонами L1, L2 и R: 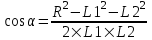 . Подставляем числа. . Подставляем числа. 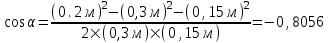 . Подставляем: . Подставляем:
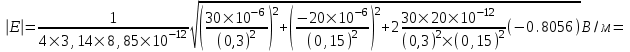
=5.86×106 В/м = 5.86 МВ/м.
|
E = ?
|
307. В вершинах правильного треугольника со стороной a=10 см находятся заряды q1=10мкКл, q2 = –20 мкКл и q3 = 30 мкКл. Определить силу F, действующую на заряд q1 со стороны двух других зарядов.
a = 10 cм
q1=10мкКл
q2=–20 мкКл
q3=30 мкКл
|
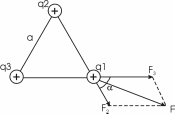
Сила с которой действует заряд q2 на заряд q1 определяется из закона Кулона: 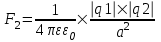 , где ε – диэлектрическая постоянная. В нашем случае она равна ε=1. , где ε – диэлектрическая постоянная. В нашем случае она равна ε=1.
Сила с которой действует заряд q3 на заряд q1:  . .
Пользуясь принципом суперпозиции получаем 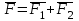 (Это векторные величины, а нам нужны скалярные). (Это векторные величины, а нам нужны скалярные).
Модуль вектора F найдем по теореме косинусов:
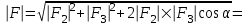
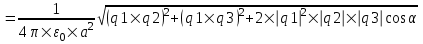 . .
Из рисунка видно, что угол α равен углу равностороннего треугольника α=60º.
Подставляем числа (переводя одновременно все величины в систему СИ).
|
F = ?
|
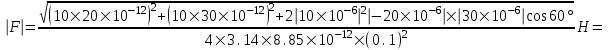
=392Н ≈ 400Н.
308. В вершинах квадрата находятся одинаковые заряды q1 = q2= q3= q4 = 8×10-10 Кл. Какой отрицательный заряд Q нужно поместить в центре квадрата, чтобы сила взаимного отталкивания положительных зарядов была уравновешена силой притяжения отрицательного заряда?
q1=q2=q3=q=
=8×10-10 Кл
|
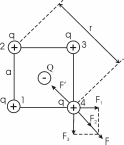
Сила с которой действует заряд q1 на заряд q4 определяется из закона Кулона: 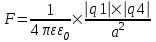 , где ε – диэлектрическая постоянная. В нашем случае она равна ε=1. , где ε – диэлектрическая постоянная. В нашем случае она равна ε=1.
В нашем случае все заряды одинаковы, поэтому сила F1=F3=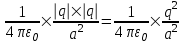 . .
Из рисунка видно, что сила F=F2+F3=F2+2×F1×cos45º (так как сила F направлена по биссектрисе угла).
Сила с которой действует заряд q2 на заряд q4 равна:  . (Здесь . (Здесь 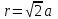 как видно из рисунка). как видно из рисунка).
Подставляем в F= F2+2×F1×cos45º и получаем  . .
Сила притяжения заряда q4 к заряду в центре квадрата равна 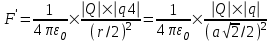 . Для того, чтобы заряд q4 был уравновешен необходимо чтобы F’=F. Поэтому . Для того, чтобы заряд q4 был уравновешен необходимо чтобы F’=F. Поэтому 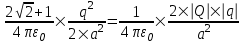 , откуда , откуда
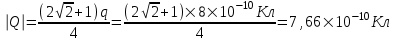 . .
|
Q = ?
|
309. На расстоянии a = 20см находятся два точечных заряда: q1 = –50 нКл и q2= 100 нКл. Определить силу F, действующую на заряд q3= –10 нКл, удаленный от обоих зарядов на одинаковое расстояние, равное a.
a = 20 cм
q1=–50нКл
q2=100 нКл
q3=–10 нКл
|
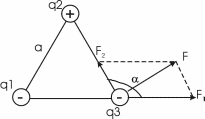
Сила с которой действует заряд q2 на заряд q3 определяется из закона Кулона: 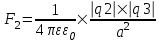 , где ε – диэлектрическая постоянная. В нашем случае она равна ε=1. , где ε – диэлектрическая постоянная. В нашем случае она равна ε=1.
Сила с которой действует заряд q1 на заряд q3: 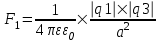 . .
Пользуясь принципом суперпозиции получаем 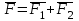 (Это векторные величины, а нам нужны скалярные). (Это векторные величины, а нам нужны скалярные).
Модуль вектора F найдем по теореме косинусов:
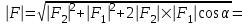
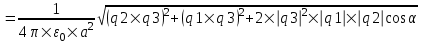 . .
Из рисунка видно, что угол α равен α=180º–60º=120º.
Подставляем числа (переводя одновременно все величины в систему СИ).
|
F = ?
|
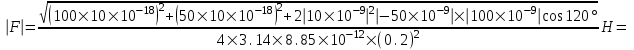
=2×10-4Н = 0,2мН.
310. Расстояние L между двумя точечными зарядами q1=2нКл и q2 = 4нКл равно 60см. Определить точку, в которую нужно поместить третий заряд q так, чтобы система зарядов находилась в равновесии. Определить заряд q и его знак. Устойчивое или неустойчивое будет равновесие?
q1=2 нКл
q2 = 4нКл
L = 60 см
|
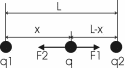
Силы взаимодействия определим из закона Кулона:
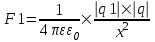 , , 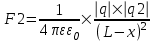 . Эти силы должны быть противоположны по направлению и одинаковыми по модулю (3-й закон Ньютона). Тогда . Эти силы должны быть противоположны по направлению и одинаковыми по модулю (3-й закон Ньютона). Тогда 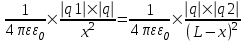 . Откуда . Откуда  . Откуда . Откуда  . Искомая величина равна . Искомая величина равна 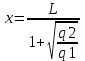 . Подставляем числа (переводя одновременно все величины в систему СИ). . Подставляем числа (переводя одновременно все величины в систему СИ). 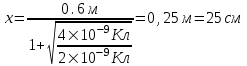 . .
То есть между зарядами на расстоянии 25 см от заряда q1.
|
x = ?
q = ?
|
Для того, чтобы заряд q1 находился в равновесии необходимо, чтобы сила взаимодействия между q1 и q2: 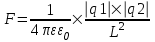 была равна силе взаимодействия между q1 и q: была равна силе взаимодействия между q1 и q: 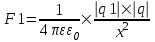 . То есть . То есть 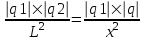 . Откуда заряд равен . Откуда заряд равен 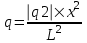 . А так как . А так как 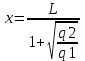 , то , то 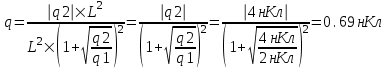 . .
Равновесие называется устойчивым, если при смещении заряда от положения равновесия возникают силы, возвращающие его в положение равновесия. Если заряд q положителен, то при смещении его влево сила F1возрастает, а сила F2 убывает. Результирующая сила, действующая на заряд q, будет направлена в противоположную сторону, в которую смещен этот заряд, т. е. вправо. Под действием этой силы заряд q будет возвращаться в положение равновесия. То же происходит и при смещении заряда q вправо. Сила F1убывает, а F2 возрастает.Геометрическая сумма сил в этом случае направлена влево. Заряд под действием этой силы будет перемещаться влево, т. е. возвращаться в положение равновесия. Таким образом, в случае положительного заряда равновесие является устойчивым. Если же заряд q будет отрицательным, то равновесие будет неустойчивым.
|
 Скачать 1.62 Mb.
Скачать 1.62 Mb.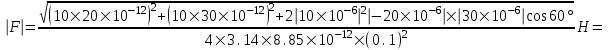
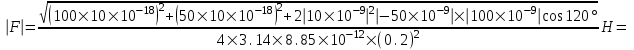
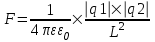 была равна силе взаимодействия между q1 и q:
была равна силе взаимодействия между q1 и q: 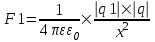 . То есть
. То есть 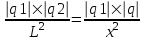 . Откуда заряд равен
. Откуда заряд равен 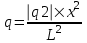 . А так как
. А так как 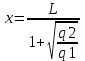 , то
, то 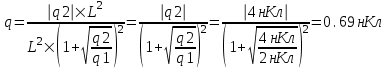 .
.
 ти три точки образуют прямоугольный треугольник т.к. L12+L22=R2.
ти три точки образуют прямоугольный треугольник т.к. L12+L22=R2.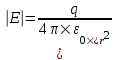 .
.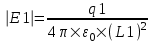 , а от второго
, а от второго 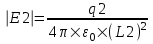 .
.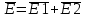 (Это векторные величины, а нам нужны скалярные). Поскольку угол между E1 и E2 прямой (так как треугольник прямоугольный), то по теореме Пифагора
(Это векторные величины, а нам нужны скалярные). Поскольку угол между E1 и E2 прямой (так как треугольник прямоугольный), то по теореме Пифагора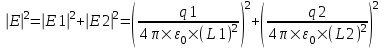 .
. 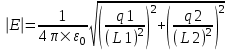
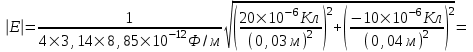
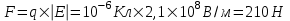 .
.
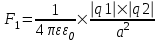 , где ε – диэлектрическая постоянная. В нашем случае она равна ε=1.
, где ε – диэлектрическая постоянная. В нашем случае она равна ε=1.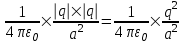 .
.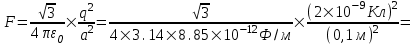
 з рисунка видно, что если заряд q будет слева или справа от обоих зарядов, то силы будут направлены в одну сторону и устойчивого положения нет. Оно возможно только когда заряд находится между q1 и q2 (см нижний рисунок).
з рисунка видно, что если заряд q будет слева или справа от обоих зарядов, то силы будут направлены в одну сторону и устойчивого положения нет. Оно возможно только когда заряд находится между q1 и q2 (см нижний рисунок).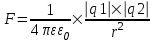 .
.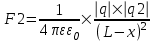 . Эти силы должны быть противоположны по направлению и одинаковыми по модулю (3-й закон Ньютона). Тогда
. Эти силы должны быть противоположны по направлению и одинаковыми по модулю (3-й закон Ньютона). Тогда 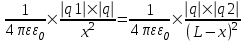 . Откуда
. Откуда  . Откуда
. Откуда  . Искомая величина равна
. Искомая величина равна  .
.  а каждый заряд действуют четыре силы:
а каждый заряд действуют четыре силы: 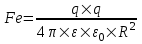 – сила Кулона, mg – сила притяжения, T – сила натяжения нити и сила Архимеда FA. Так как заряды находятся в равновесии, то из
– сила Кулона, mg – сила притяжения, T – сила натяжения нити и сила Архимеда FA. Так как заряды находятся в равновесии, то из 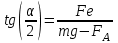 - условие равновесия заряда. Сила Архимеда равна
- условие равновесия заряда. Сила Архимеда равна 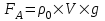 , где V – объем шарика. Тогда масса шарика равна m=ρ×V. Поэтому
, где V – объем шарика. Тогда масса шарика равна m=ρ×V. Поэтому 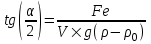 .
.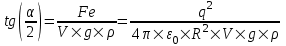 .
.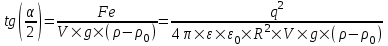 .
.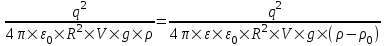
 . Подставляем числа.
. Подставляем числа. 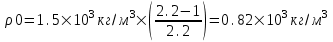 .
.
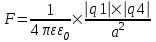 , где ε – диэлектрическая постоянная. В нашем случае она равна ε=1.
, где ε – диэлектрическая постоянная. В нашем случае она равна ε=1. . (Здесь
. (Здесь 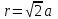 как видно из рисунка).
как видно из рисунка).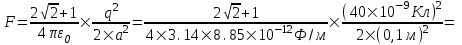

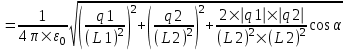 .
.  десь угол α – угол между векторами E1 и E2, который может быть найден из треугольника со сторонами L1, L2 и R:
десь угол α – угол между векторами E1 и E2, который может быть найден из треугольника со сторонами L1, L2 и R: 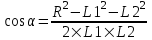 . Подставляем числа.
. Подставляем числа. 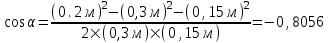 . Подставляем:
. Подставляем: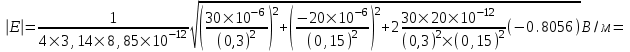

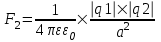 , где ε – диэлектрическая постоянная. В нашем случае она равна ε=1.
, где ε – диэлектрическая постоянная. В нашем случае она равна ε=1. .
.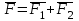 (Это векторные величины, а нам нужны скалярные).
(Это векторные величины, а нам нужны скалярные). 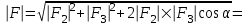
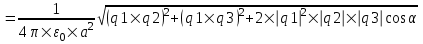 .
. 
 .
.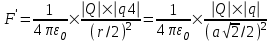 . Для того, чтобы заряд q4 был уравновешен необходимо чтобы F’=F. Поэтому
. Для того, чтобы заряд q4 был уравновешен необходимо чтобы F’=F. Поэтому 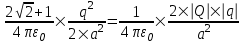 , откуда
, откуда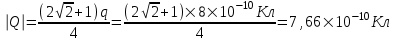 .
.
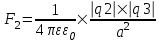 , где ε – диэлектрическая постоянная. В нашем случае она равна ε=1.
, где ε – диэлектрическая постоянная. В нашем случае она равна ε=1.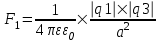 .
.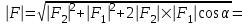
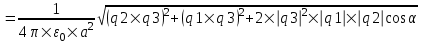 .
. 
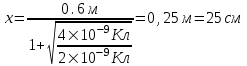 .
.