359. Пространство между пластинами плоского конденсатора заполнено двумя слоями диэлектриков: слоем стекла толщиной d1 = 0.2 см и слоем парафина толщиной d2=0.3 см. Разность потенциалов между обкладками U = 300В. Определить напряженность поля и падение потенциала в каждом из слоев.
d1 =0.2 см
d2=0.3 см
U = 300В
ε1 = 6
ε2 = 2
|
Известно, что вектор электрического смещения D не претерпевает изменений в любой диэлектрической среде. Поэтому D=ε0×ε1×E1= ε0×ε2×E2. Откуда 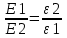 . .
С другой стороны разность потенциалов между обкладками равно 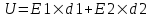 . .
Учитываем что 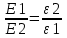 и находим и находим 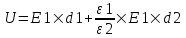 . Откуда искомая напряженность поля на слое стекла равна . Откуда искомая напряженность поля на слое стекла равна 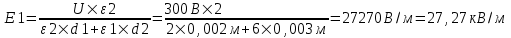 . .
Тогда 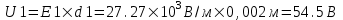 . .
Из формулы 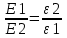 находим находим 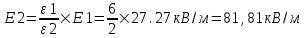 . .
Тогда 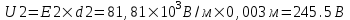 . .
|
E1 = ?
E2 = ?
U1 = ?
U2 = ?
|
360. Плоский конденсатор с площадью пластин S=200 см2 каждая заряжен до разности потенциалов U=2 кВ. Расстояние между пластинами d=2 см. Диэлектрик – стекло. Определить энергию W поля конденсатора и плотность ω энергии поля.
d = 2 cм
U = 2 кВ
ε = 2.25
S=200 см2
|
Объемная плотность энергии электрического поля 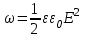 , где ε0 = 8,85×10-12Ф/м – электрическая постоянная, E=U/d – напряженность поля. Тогда , где ε0 = 8,85×10-12Ф/м – электрическая постоянная, E=U/d – напряженность поля. Тогда 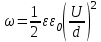 . Подставляем числа (переводя одновременно все величины в систему СИ). . Подставляем числа (переводя одновременно все величины в систему СИ).
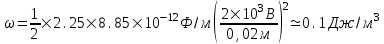 . .
Энергия конденсатора равна произведению объемной плотности энергии на объем конденсатора:  , где S – площадь пластин. Тогда , где S – площадь пластин. Тогда 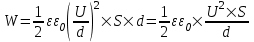 . .
Подставляем числа (переводя одновременно все величины в систему СИ).
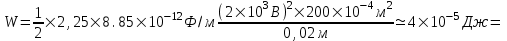
= . .
|
W = ?
ω = ?
|
363. От батареи, э. д. с. которой ε=600 В, требуется передать энергию на расстояние L=1км. Потребляемая мощность P=5 кВт. Найти минимальные потери мощности в сети, если диаметр медных подводящих проводов d=0,5 см.
ε=600 В
P = 5 кВт
L = 1 км
d = 0,5 см
|
Известно, что относительная потеря мощности в проводах 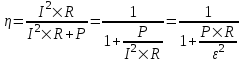 , где ε – э.д.с. батареи, P – потребляемая мощность. Сопротивление проводника , где ε – э.д.с. батареи, P – потребляемая мощность. Сопротивление проводника 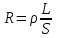 , где L – длина проводника, S – площадь сечения, ρ – удельное сопротивление , где L – длина проводника, S – площадь сечения, ρ – удельное сопротивление
(ρ = 1,7×10-8Ом×м – для меди).
Так как площадь сечения проводов 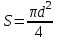 , то в нашем случае , то в нашем случае 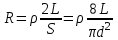 (мы подставили 2L вместо L так как провода два). Подставляем (мы подставили 2L вместо L так как провода два). Подставляем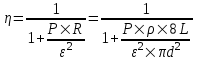 . .
Подставляем числа (переводя одновременно все величины в систему СИ). 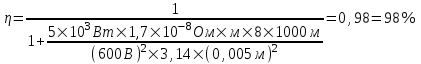 . .
|
η = ?
|
364. При внешнем сопротивлении R1 = 8 Ом сила тока в цепи I1=0,8 А, при сопротивлении R2=15 Ом сила тока I2=0,5 А. Определить силу тока короткого замыкания источника э. д. с.
R1 = 8 Ом
R2 = 15 Ом
I1 = 0.8А
I2 = 0.5А
|
Из закона Ома известно 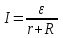 , где ε – величина ЭДС источника, r – внутреннее сопротивление ЭДС источника, сопротивление R– это внешнее сопротивление. Откуда при R=0 получаем ток короткого замыкания , где ε – величина ЭДС источника, r – внутреннее сопротивление ЭДС источника, сопротивление R– это внешнее сопротивление. Откуда при R=0 получаем ток короткого замыкания 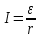 . .
В первом случае 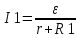 . Во втором случае . Во втором случае 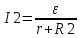 (величины ε и r постоянны). Из этих уравнений находим (величины ε и r постоянны). Из этих уравнений находим 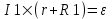 и и 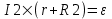 , поэтому , поэтому 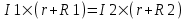 . Откуда находим величину внутреннего сопротивления . Откуда находим величину внутреннего сопротивления  . .
Из уравнения короткого замыкания имеем ε=I×r. С другой стороны из 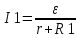 имеем имеем 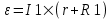 . Поэтому . Поэтому 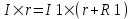 . Из этого уравнения находим . Из этого уравнения находим 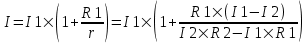 . .
Подставляем числа: 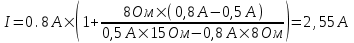 . .
|
I = ?
|
365. Э. д. с. батареи ε = 24 В. Наибольшая сила тока, которую может дать батарея, Iмакс=10А. Определить максимальную мощность Рмакс, которая может выделяться во внешней цепи.
ε = 24 В
Iмакс=10А
|
Из закона Ома известно 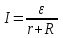 , где ε – величина ЭДС источника, r – внутреннее сопротивление ЭДС источника, сопротивление R– это внешнее сопротивление. При R=0 ток будет максимальным и равным , где ε – величина ЭДС источника, r – внутреннее сопротивление ЭДС источника, сопротивление R– это внешнее сопротивление. При R=0 ток будет максимальным и равным 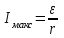 , откуда внутреннее сопротивление равно , откуда внутреннее сопротивление равно 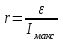 . .
По определению мощность 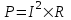 , поэтому , поэтому  . .
Найдем при каком R мощность будет максимальна. Для этого приравняем производную P по R нулю:
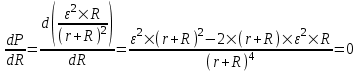 . .
Поэтому 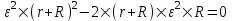 , откуда , откуда 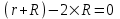 . То есть при внешнем сопротивлении . То есть при внешнем сопротивлении 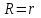 мощность P будет максимальной и будет равна: мощность P будет максимальной и будет равна: 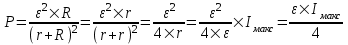 . .
Подставляем числа. 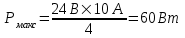 . .
|
Рмакс = ?
|
366. Аккумулятор с ЭДС ε=12 В заряжается от сети постоянного тока с напряжением U=15В. Определить напряжение на клеммах аккумулятора, если его внутреннее сопротивление R=10Ом.
ε=12 В
U=15В
R=10Ом
|
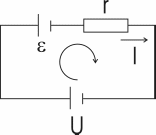
Для расчета разветвленных цепей применяются законы (правила) Кирхгофа. Выберем произвольное направление тока, как оно показано на рисунке, и условимся обходить контур по направлению тока (оно изображено внутри контура полукругом).
По второму закону Кирхгофа для контура запишем 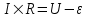 , откуда ток в цепи равен , откуда ток в цепи равен 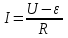 . .
Тогда напряжение на сопротивлении R равно 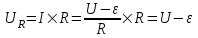
Подставляем числа. 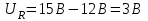 . .
|
UR=?
|
367. От источника с напряжением U = 800 В необходимо передать потребителю мощность Р=10 кВт на некоторое расстояние. Какое наибольшее сопротивление может иметь линия передачи, чтобы потери энергии в ней не превышали 10% от передаваемой мощности?
U=800 В
P = 10 кВт
η = 0.1
|
Известно, что относительная потеря мощности в проводах 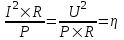 , где U – напряжение генератора, P – потребляемая мощность. Отсюда находим , где U – напряжение генератора, P – потребляемая мощность. Отсюда находим 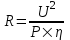 . .
Подставляем числа. 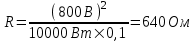 . .
|
R = ?
|
368. При включении электромотора в сеть с напряжением U = 220 В он потребляет ток I =5А. Определить мощность, потребляемую мотором, и его КПД, если сопротивление R обмотки мотора равно 6 Ом.
U = 220 В
I =5А
R=6 Ом
|
Мощность потребляемая мотором равна 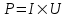 . .
Подставляем числа. 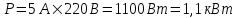 . .
Полезная мощность мотора (которую он вырабатывает) равна P–P0, где 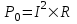 - потеря мощности на выделении тепла на сопротивлении R. - потеря мощности на выделении тепла на сопротивлении R.
Тогда КПД равен 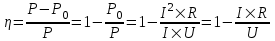 . .
Подставляем числа. 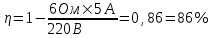 . .
|
P=?
η=?
|
369. В сеть с напряжением U=100 В включили катушку с сопротивлением R1=2 кОм и вольтметр, соединенные последовательно. Показание вольтметра U1 = 80 В. Когда катушку заменили другой, вольтметр показал U2 = 60 В. Определить сопротивление другой катушки.
R1 = 2 кОм
U=100 В
U1 = 80В
U2 = 60В
|
Из закона Ома известно 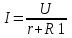 , где U – напряжение в сети, r – сопротивление вольтметра, сопротивление R1 – это сопротивление катушки. Напряжение, которое показывает вольтметр равно , где U – напряжение в сети, r – сопротивление вольтметра, сопротивление R1 – это сопротивление катушки. Напряжение, которое показывает вольтметр равно 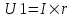 , поэтому , поэтому 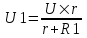 , откуда сопротивление вольтметра , откуда сопротивление вольтметра 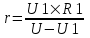 . .
Во втором случае напряжение, которое показывает вольтметр равно 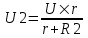 , откуда сопротивление второй катушки равно , откуда сопротивление второй катушки равно 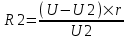 . Подставляем сюда . Подставляем сюда 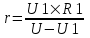 и получаем и получаем 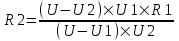 . .
Подставляем числа. 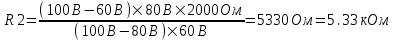 . .
|
R2 = ?
|
370. ЭДС батареи ε= 12 В. При силе тока I= 4 А к. п. д. батареи η = 0,6. Определить внутреннее сопротивление r батареи.
ε = 12 В
I = 4A
η=0.6
|
По определению к.п.д. источника тока есть отношение 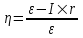 , где ε – э.д.с. источника, I×r – потеря напряжения на внутреннем сопротивлении r. , где ε – э.д.с. источника, I×r – потеря напряжения на внутреннем сопротивлении r.
Тогда 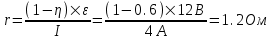 . .
|
r = ?
|
375. Сила тока в проводнике изменяется со временем по закону I = I0sinωt. Найти заряд Q, проходящий через поперечное сечение проводника за время t, равное половине периода Т, если начальная сила тока I0 = 10 А, циклическая частота ω = 50πс-1.
I = I0sinωt
I0 = 10 А
ω = 50πс-1
t=T/2
|
Сила тока равна по определению 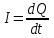 , где dQ – проходящий заряд, dt – время за которое проходит заряд. Поэтому , где dQ – проходящий заряд, dt – время за которое проходит заряд. Поэтому 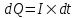 . .
Полный заряд равен интегралу 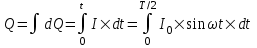 . .
Вычисляем его 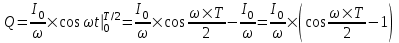 . .
Круговая частота равна по определению 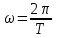 . Поэтому . Поэтому 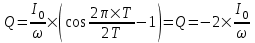 . .
Подставляем числа. 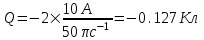 . .
|
Q=?
|
376. За время T = 10 с при равномерно возрастающей силе тока от нуля до некоторого максимума в проводнике выделилось количество теплоты Q = 40 кДж. Определить среднюю силу тока в проводнике, если его сопротивление R = 25 Ом.
T=10с
I1=0A
Q=40 кДж
R=25Ом
|
Количество теплоты, выделяющееся в проводнике при прохождении тока за время dt равно dQ=I2×R×dt.
Зависимость тока от времени линейная: 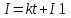 , где , где 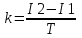 . .
Тогда полная теплота равна интегралу
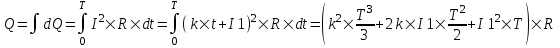 . .
Так как 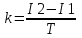 , то , то 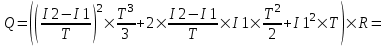
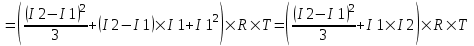 . .
Так как I1=0, то 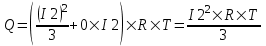 . Откуда конечный ток равен . Откуда конечный ток равен 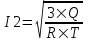 . Среднее значение тока равно . Среднее значение тока равно  . .
Подставляем числа. 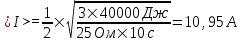 . .
|
= ?
|
377. За время T = 8 с при равномерно возраставшей силе тока в проводнике сопротивлением R = 8 Ом выделилось количество теплоты Q = 500 Дж. Определить заряд q, проходящий в проводнике, если сила тока в начальный момент времени равна нулю.
T=8с
I1=0A
Q=500Дж
R=8Ом
|
Количество теплоты, выделяющееся в проводнике при прохождении тока за время dt равно dQ=I2×R×dt. Зависимость тока от времени линейная: 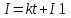 , где , где 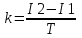 . .
Тогда полная теплота равна интегралу
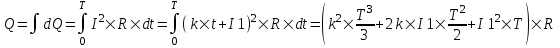 . .
Так как 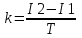 , то , то 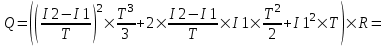
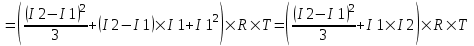 . .
Так как I1=0, то 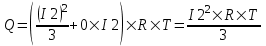 . Откуда конечный ток равен . Откуда конечный ток равен 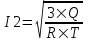 . Тогда зависимость тока от времени следующая: . Тогда зависимость тока от времени следующая: 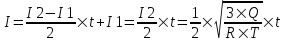
Сила тока равна по определению 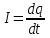 , где dq – проходящий заряд, dt – время за которое проходит заряд. Поэтому , где dq – проходящий заряд, dt – время за которое проходит заряд. Поэтому 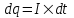 . .
Полный заряд равен интегралу 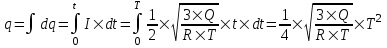 . .
Подставляем числа. 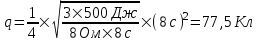 . .
|
q = ?
|
378. Определить количество теплоты Q, выделившееся за время T = 10 с в проводнике сопротивлением R = 10 Ом, если сила тока в нем, равномерно уменьшаясь, изменилась от I1= 10 А до I2 = 0.
T=10с
I1=10A
I2=0A
R=10Ом
|
Количество теплоты, выделяющееся в проводнике при прохождении тока за время dt равно dQ=I2×R×dt.
Зависимость тока от времени линейная: 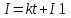 , где , где 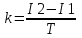 . .
Тогда полная теплота равна интегралу
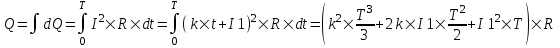 . .
Так как 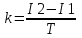 , то , то 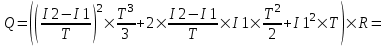
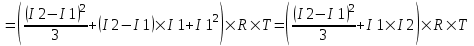 . .
Подставляем числа. 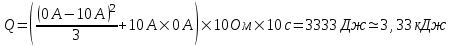 . .
|
Q = ?
|
379. Сила тока в цепи изменяется по закону I = I0sinωt. Определить количество теплоты, которое выделится в проводнике сопротивлением R=10 Ом за время, равное четверти периода от t1 = 0 до t2 = Т/4, где T=10c.
T=10 с
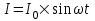
R=10 Ом
t1 = 0
t2 = Т/4
|
Количество теплоты, выделяющееся в проводнике при прохождении тока за время dt равно dQ=I2×R×dt.
Тогда полная теплота равна интегралу
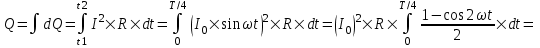
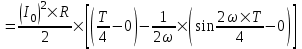 . .
Угловая частота равна по определению 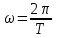 , поэтому , поэтому 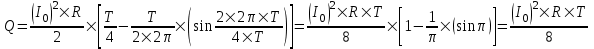
Подставляем числа.
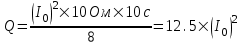 . .
Для численного ответа необходимо знать I0.
|
Q = ?
|
380. Сила тока в проводнике изменяется со временем по закону  . Определить количество теплоты, которое выделится в проводнике сопротивлением R = 20 Ом за время, в течение которого ток уменьшится в е раз. Коэффициент α принять равным 2×10-2с-1. . Определить количество теплоты, которое выделится в проводнике сопротивлением R = 20 Ом за время, в течение которого ток уменьшится в е раз. Коэффициент α принять равным 2×10-2с-1.
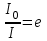

α= 2×102с-1
R = 20 Ом
|
Количество теплоты, выделяющееся в проводнике при прохождении тока за время dt равно dQ=I2×R×dt.
Тогда полная теплота равна интегралу
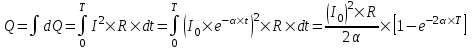 . .
Так как 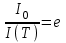 , то , то 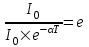 , откуда , откуда 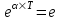 . Поэтому α×T=1. . Поэтому α×T=1.
Тогда теплота равна 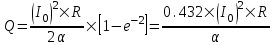
Подставляем числа.
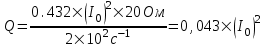 . .
Для численного ответа необходимо знать I0.
|
Q = ?
| |
 Скачать 1.62 Mb.
Скачать 1.62 Mb. . Определить количество теплоты, которое выделится в проводнике сопротивлением R = 20 Ом за время, в течение которого ток уменьшится в е раз. Коэффициент α принять равным 2×10-2с-1.
. Определить количество теплоты, которое выделится в проводнике сопротивлением R = 20 Ом за время, в течение которого ток уменьшится в е раз. Коэффициент α принять равным 2×10-2с-1.
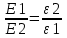 .
.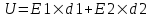 .
. 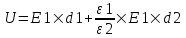 . Откуда искомая напряженность поля на слое стекла равна
. Откуда искомая напряженность поля на слое стекла равна 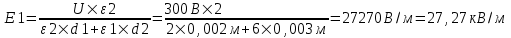 .
.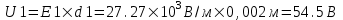 .
.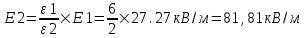 .
.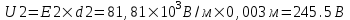 .
.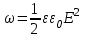 , где ε0 = 8,85×10-12Ф/м – электрическая постоянная, E=U/d – напряженность поля. Тогда
, где ε0 = 8,85×10-12Ф/м – электрическая постоянная, E=U/d – напряженность поля. Тогда 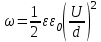 . Подставляем числа (переводя одновременно все величины в систему СИ).
. Подставляем числа (переводя одновременно все величины в систему СИ). 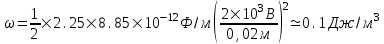 .
. , где S – площадь пластин. Тогда
, где S – площадь пластин. Тогда 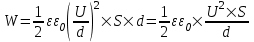 .
.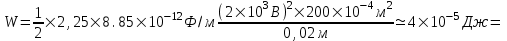
 .
.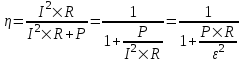 , где ε – э.д.с. батареи, P – потребляемая мощность. Сопротивление проводника
, где ε – э.д.с. батареи, P – потребляемая мощность. Сопротивление проводника 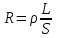 , где L – длина проводника, S – площадь сечения, ρ – удельное сопротивление
, где L – длина проводника, S – площадь сечения, ρ – удельное сопротивление 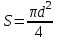 , то в нашем случае
, то в нашем случае 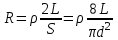 (мы подставили 2L вместо L так как провода два). Подставляем
(мы подставили 2L вместо L так как провода два). Подставляем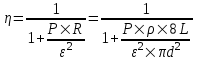 .
.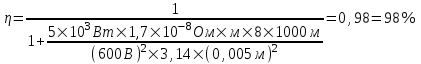 .
.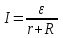 , где ε – величина ЭДС источника, r – внутреннее сопротивление ЭДС источника, сопротивление R– это внешнее сопротивление. Откуда при R=0 получаем ток короткого замыкания
, где ε – величина ЭДС источника, r – внутреннее сопротивление ЭДС источника, сопротивление R– это внешнее сопротивление. Откуда при R=0 получаем ток короткого замыкания 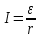 .
. 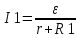 . Во втором случае
. Во втором случае 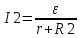 (величины ε и r постоянны). Из этих уравнений находим
(величины ε и r постоянны). Из этих уравнений находим 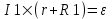 и
и 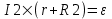 , поэтому
, поэтому 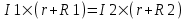 . Откуда находим величину внутреннего сопротивления
. Откуда находим величину внутреннего сопротивления  .
. 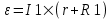 . Поэтому
. Поэтому 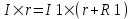 . Из этого уравнения находим
. Из этого уравнения находим 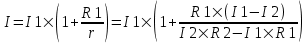 .
.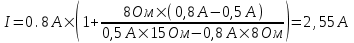 .
.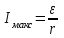 , откуда внутреннее сопротивление равно
, откуда внутреннее сопротивление равно 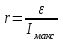 .
.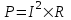 , поэтому
, поэтому  .
. 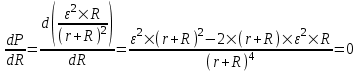 .
. 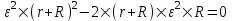 , откуда
, откуда 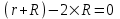 . То есть при внешнем сопротивлении
. То есть при внешнем сопротивлении 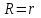 мощность P будет максимальной и будет равна:
мощность P будет максимальной и будет равна: 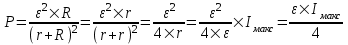 .
.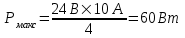 .
.
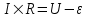 , откуда ток в цепи равен
, откуда ток в цепи равен 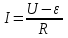 .
.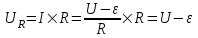
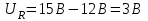 .
.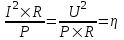 , где U – напряжение генератора, P – потребляемая мощность. Отсюда находим
, где U – напряжение генератора, P – потребляемая мощность. Отсюда находим 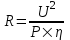 .
.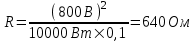 .
.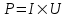 .
.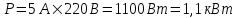 .
.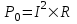 - потеря мощности на выделении тепла на сопротивлении R.
- потеря мощности на выделении тепла на сопротивлении R. 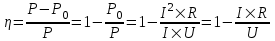 .
.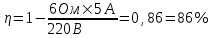 .
.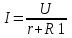 , где U – напряжение в сети, r –
, где U – напряжение в сети, r – 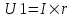 , поэтому
, поэтому 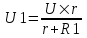 , откуда сопротивление вольтметра
, откуда сопротивление вольтметра 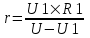 .
.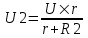 , откуда сопротивление второй катушки равно
, откуда сопротивление второй катушки равно 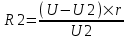 . Подставляем сюда
. Подставляем сюда 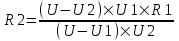 .
. 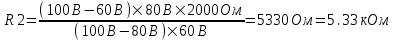 .
.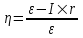 , где ε – э.д.с. источника, I×r – потеря напряжения на внутреннем сопротивлении r.
, где ε – э.д.с. источника, I×r – потеря напряжения на внутреннем сопротивлении r. 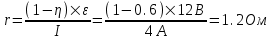 .
.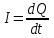 , где dQ – проходящий заряд, dt – время за которое проходит заряд. Поэтому
, где dQ – проходящий заряд, dt – время за которое проходит заряд. Поэтому 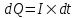 .
.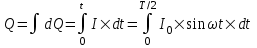 .
.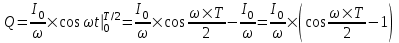 .
.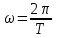 . Поэтому
. Поэтому 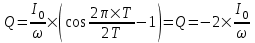 .
.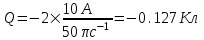 .
.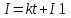 , где
, где 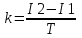 .
.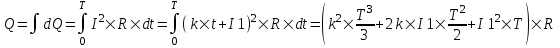 .
.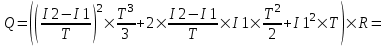
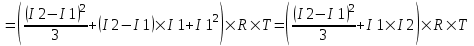 .
.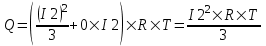 . Откуда конечный ток равен
. Откуда конечный ток равен 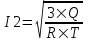 . Среднее значение тока равно
. Среднее значение тока равно  .
.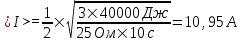 .
.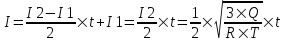
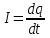 , где dq – проходящий заряд, dt – время за которое проходит заряд. Поэтому
, где dq – проходящий заряд, dt – время за которое проходит заряд. Поэтому 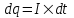 .
.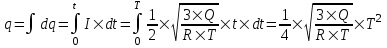 .
.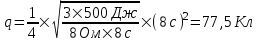 .
.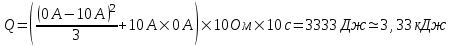 .
.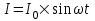
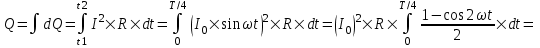
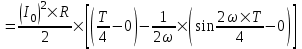 .
.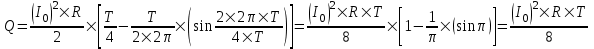
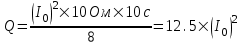 .
.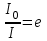
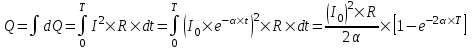 .
.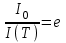 , то
, то 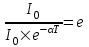 , откуда
, откуда 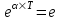 . Поэтому α×T=1.
. Поэтому α×T=1.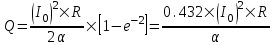
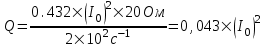 .
.